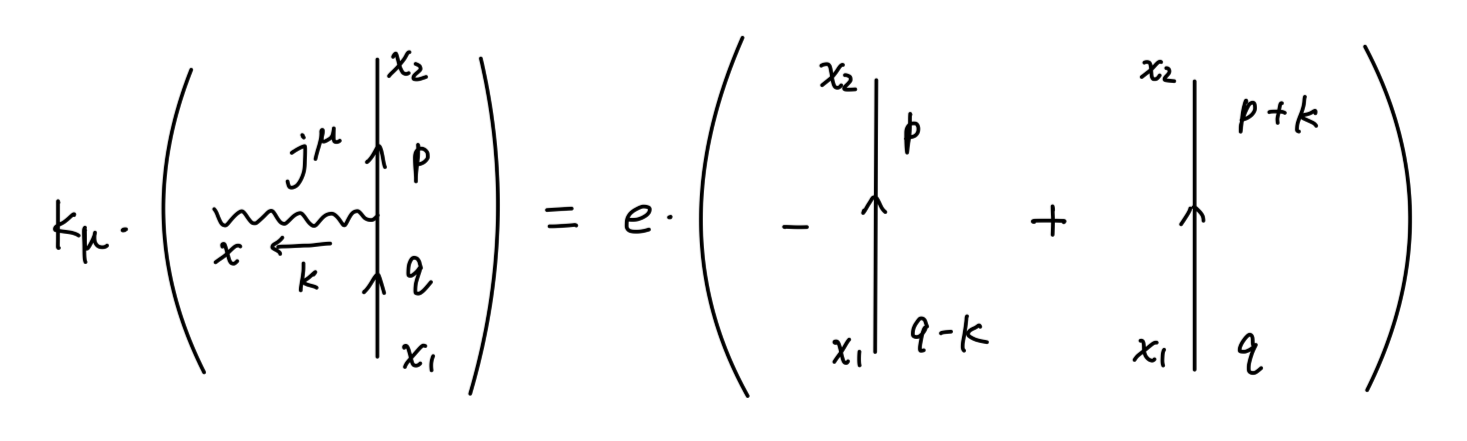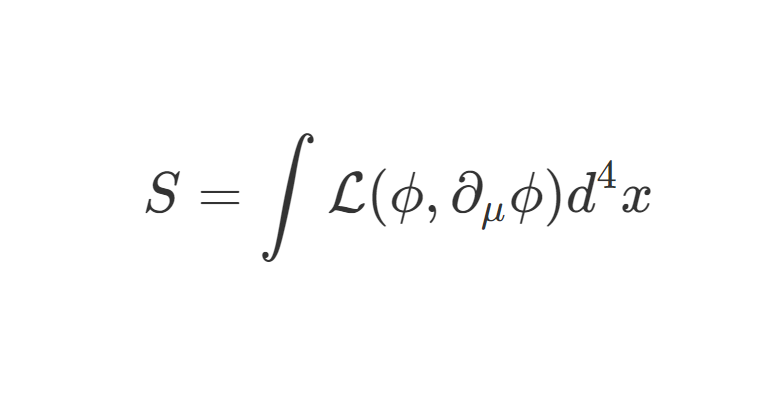路径积分表述与对称性
在前面几篇中,我们使用了路径积分表述对标量场、矢量场、旋量场进行了量子化。这种方法完全基于哈密顿量的结构。那么如果系统的拉氏量具有某种对称性,相应的路径积分表述中也能够保持这种对称性。在经典力学中,可以使用最小作用量原理推导出了系统的运动方程——欧拉-拉格朗日方程,利用 Noether 定理将守恒量与对称性联系起来。现在,我们想使用路径积分表述去探索量子场论中的运动方程、守恒律。
运动方程
不妨考虑一个自由标量场:
L=21(∂μϕ)2−21m2ϕ2
考虑如下的三点关联函数:
⟨Ω∣Tϕ(x1)ϕ(x2)ϕ(x3)∣Ω⟩=Z−1∫Dϕei∫d4xL[ϕ]ϕ(x1)ϕ(x2)ϕ(x3)
在理论力学中,我们使用了最小作用量原理推导出了运动方程:拉格朗日方程。现在我们也认为真实运动所对应的作用量取极值来推导运动方程。即考虑如下无穷小变换:
ϕ(x)→ϕ′(x)=ϕ(x)+ϵ(x)
这个 shift 不改变积分测度:
Dϕ′=Dϕ
得到:对于真实运动将有下式成立
==∫Dϕei∫d4xL[ϕ]ϕ(x1)ϕ(x2)ϕ(x3)∫Dϕei∫d4xL[ϕ′]ϕ′(x1)ϕ′(x2)ϕ′(x3)∫Dϕei∫d4xL[ϕ]{ϕ(x1)ϕ(x2)ϕ(x3)+(i∫d4xϵ(x)(−∂2−m2)ϕ(x)ϕ(x1)ϕ(x2)ϕ(x3))+ϵ(x1)ϕ(x2)ϕ(x3)+ϕ(x1)ϵ(x2)ϕ(x3)+ϕ(x1)ϕ(x2)ϵ(x3)}
其中 ϵ(x2) 可以写为:
ϵ(x2)=∫d4xϵ(x)δ(x−x1)
那么就可以将上式子的后四项写成同样的形式。可以得到:
0=∫Dϕei∫d4xL[(∂2+m2)ϕ(x)ϕ(x1)ϕ(x2)ϕ(x3)+iδ(x−x1)ϕ(x2)ϕ(x3)+iϕ(x1)δ(x−x2)ϕ(x3)+iϕ(x1)ϕ(x2)δ(x−x3)]
若我们仅考虑只有 ϕ(x1) 的情形,类比上式,一点关联函数 ⟨Ω∣ϕ(x1)∣Ω⟩ 将满足如下方程:
0=∫Dϕei∫d4xL[(∂2+m2)ϕ(x)ϕ(x1)+iδ(x−x1)]
即有:
(∂2+m2)⟨Ω∣Tϕ(x)ϕ(x1)∣Ω⟩=−iδ(x−x1)
这就是一点关联函数将满足的运动方程。我们注意到:其中式子左边带有 Klein-Gordon 算子 ∂2+m2,右边出现了 δ 函数。这说明费曼传播子:Ω∣Tϕ(x)ϕ(x1)∣Ω⟩ 是 Klein-Gordon 算子的格林函数。
对于一般的 n 点关联函数,实际上有:
(∂2+m2)⟨Ω∣Tϕ(x)ϕ(x1)⋯ϕ(xn)∣Ω⟩=i=1∑n⟨Ω∣Tϕ(x1)⋯(−iδ(x−xi))⋯ϕ(xn)∣Ω⟩
上述结论是容易进行推广的:
0=∫Dφei∫d4xL{(i∫d4xϵ(x)δφ(x)δ∫d4x′L)⋅φ(x1)⋯φ(xn)+i=1∑nφ(x1)⋯δ(x−xi)⋯φ(xn)}(1)
考虑到:
δφ(x)δ∫d4x′L=∂φ∂L−∂μ∂(∂μφ)∂L
这正是 φ 需要满足的拉格朗日方程。(1) 可以写为:
⟨(δφ(x)δ∫d4x′L)φ(x1)⋯φ(xn)⟩=i=1∑n⟨φ(x1)⋯(iδ(x−xi))⋯φ(xn)⟩
其中 ⟨⋯⟩ 表示关联函数,其中的场量作时序积。上述方程称为 Schwinger-Dyson 方程,是经典场论中场的运动方程在量子场论中的类比。
我们如果用 F[φ] 表示一个有关场量 φ 的泛函。那么 Schwinger-Dyson 方程 方程可以写为:
⟨δφδF[φ]⟩=−i⟨F[φ]δφδS[φ]⟩(2)
守恒量与对称性
在经典力学中,Noether 定理说明了守恒量与对称性的关系。现在我们利用路径积分表述,在量子场论中进行相关的分析。以自由复值场为例:
L=∣∂μϕ∣2−m∣ϕ∣2(3)
该拉氏量在变换 ϕ→eiαϕ 下不变。该变换的无穷小形式为:
ϕ(x)→ϕ(x)′=ϕ(x)+iα(x)ϕ(x)(4)
在该变换下,容易得到积分测度不变。既然拉氏量不变,那么两点关联函数也应当不变。即:
∫Dϕei∫d4xL[ϕ]ϕ(x1)ϕ∗(x2)=∫Dϕei∫d4xL[ϕ′]ϕ′(x1)ϕ′∗(x2)∣ϕ′=(1+iα)ϕ=∫Dϕei∫d4xL[ϕ]{i∫d4x[(∂μα)⋅i(ϕ∂μϕ∗−ϕ∗∂μϕ)ϕ(x1)ϕ∗(x2)+[iα(x1)ϕ(x1)]ϕ∗(x2)+ϕ(x1)[−iα(x2)ϕ∗(x2)]}
我们注意到,上式中正包含了矢量流:
jμ=i(ϕ∂μϕ∗−ϕ∗∂μϕ)
将该式进行分部积分,可以得到:
⟨∂μjμϕ(x1)ϕ∗(x2)⟩=(−i)⟨(iϕ(x1)δ(x−x1)ϕ∗(x2)+ϕ(x1)(−iϕ∗(x2)δ(x−x2))⟩
这就是经典的流守恒方程在场论中的类比。
不难讨论一般情况,考虑对场量做一个无穷小变换:
φa(x)→φa(x)+iϵΔφa(x)
假设作用量在该变换下保持不变,那么拉氏量至多改变一个表面项:
L[φ]→L[φ]+ϵ∂μJμ
如果 ϵ 是一个依赖于 x 的量,那么拉氏量将改变为:
L[φ]→L[φ]+(∂μϵ)Δφa∂(∂μφa)∂L+ϵ∂μJμ
上式中重复的指标 a 代表求和。因此可以得到:
δϵ(x)δ∫d4xL[φ+ϵΔφ]=∂μJμ−Δφa∂μ∂(∂μφa)∂L=−∂μjμ
其中:
jμ=∂(∂μφa)∂LΔφa−Jμ
利用路径积分表述进行推导,得到相应的 Schwinger-Dyson 方程:
⟨∂μjμφa(x1)φb(x2)⟩=(−i)⟨(Δφa(x1)δ(x−x1)φb(x2))+(φa(x1)(φb(x2)δ(x−x2))⟩
Ward 等式
最后我们来考虑以下与 QED 的全局对称性相关的 Schwinger-Dyson 方程。考虑进行如下变换 (U(1)):
ψ(x)→(1+ieα(x))ψ(x)
对应的拉氏量成为:
L→L−e∂μαψˉγμψ
使用泛函积分计算两点关联函数,并进行类似推导,将得到对应的泛函积分将满足如下等式:
0=∫DψˉDψDAei∫d4xL{−i∫d4x∂μα(x)[jμ(x)ψ(x1)ψˉ(x2)]+(ieα(x1)ψ(x1))ψˉ(x2)+ψ(x1)(−ieα(x2)ψˉ(x2))}
其中:
jμ=eψˉγμψ
通过除以 Z,并进行分部积分,可以把得到的结果写为:
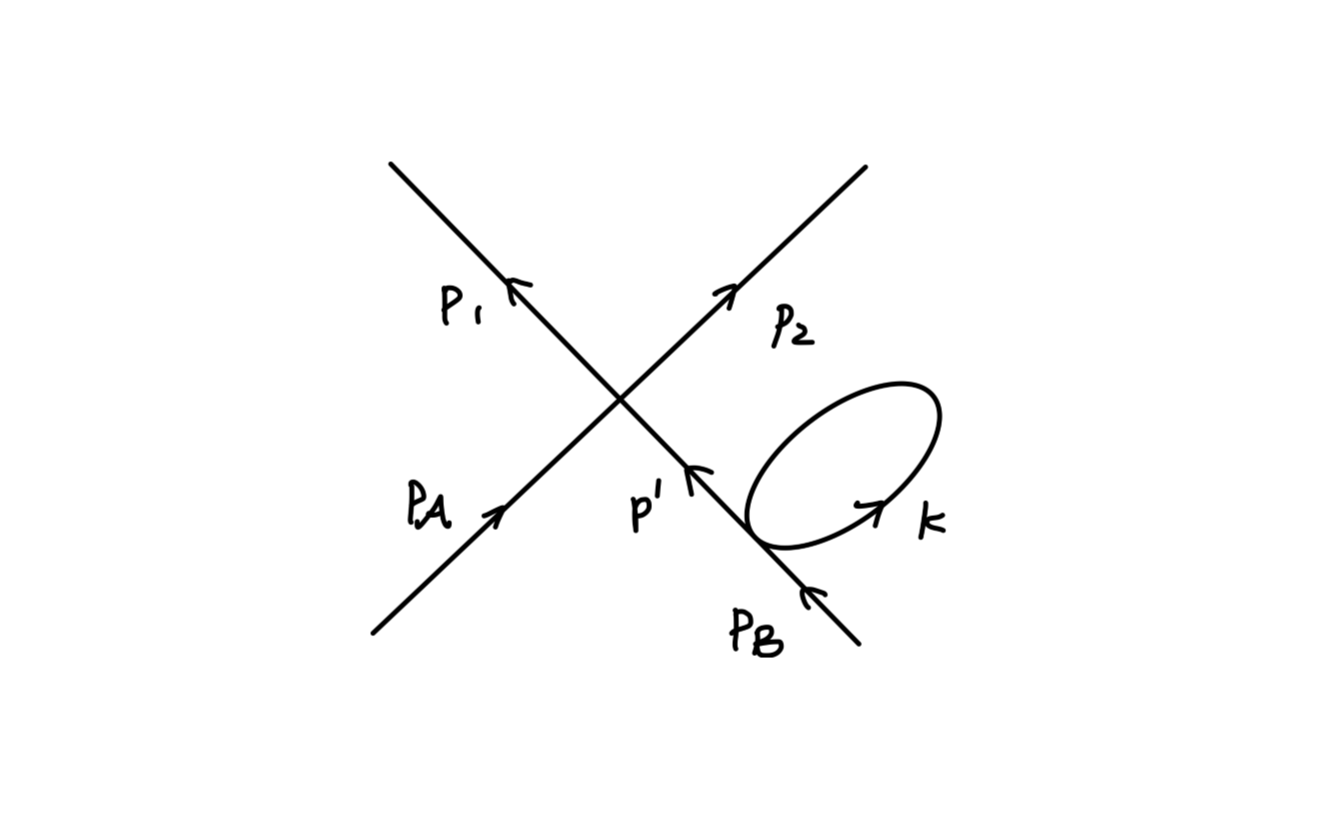
i∂μ⟨0∣Tjμ(x)ψ(x1)ψˉ(x2)∣0⟩=−ieδ(x−x1)⟨0∣Tψ(x1)ψˉ(x2)∣0⟩+ieδ(x−x2)⟨0∣Tψ(x1)ψˉ(x2)∣0⟩(5)
通过如下傅里叶变换:
∫d4xe−ik⋅x∫d4x1e+iq⋅x1∫d4x2e−ip⋅x2
我们可以将上式的每一项与一个费曼图关联起来:
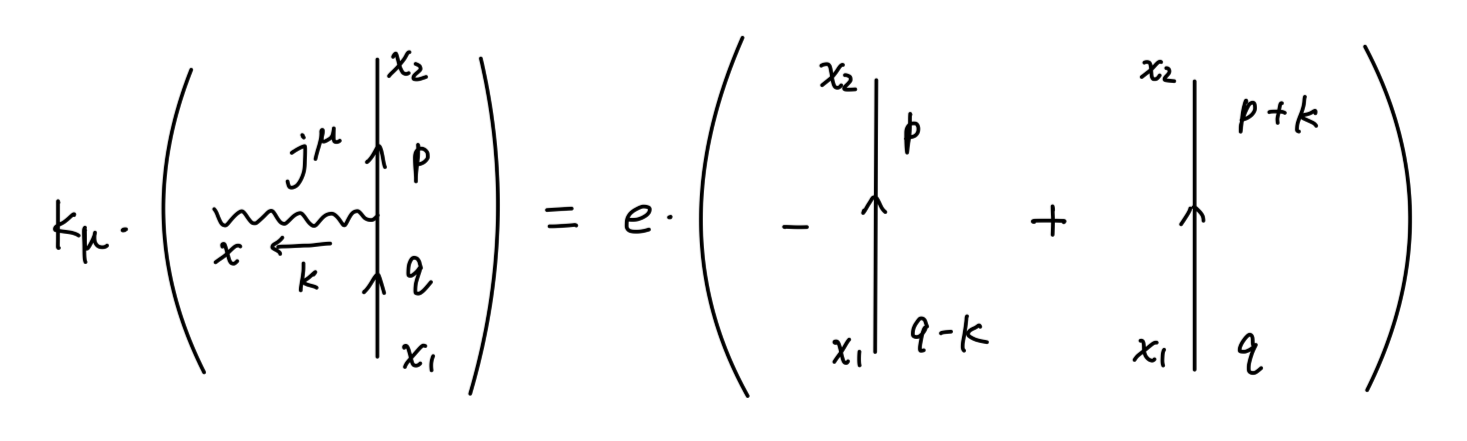
可以把 (5) 变换为我们所熟悉的形式:
−ikμMμ(k;p,q)=−ieM0(p;q−k)+ieM0(p+k;q)
这就是 Ward 等式,说明这是 U(1) 对称性所给出的必然结果。