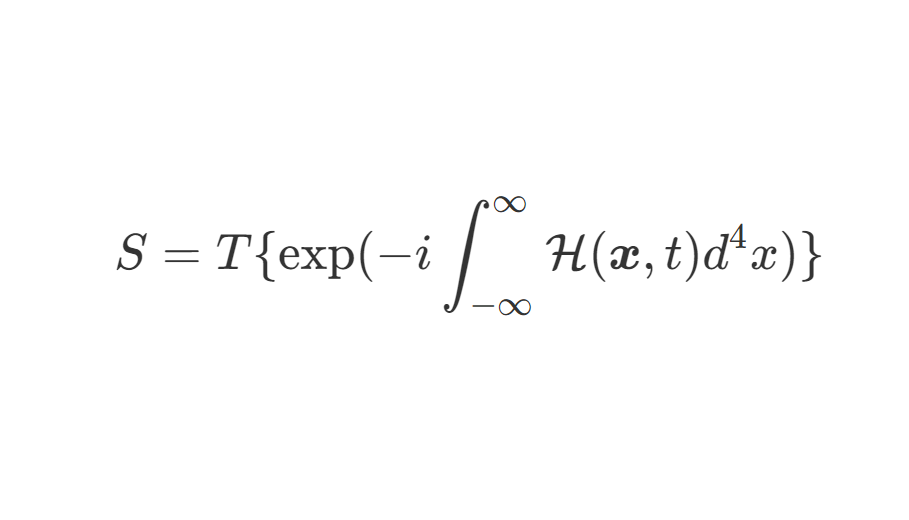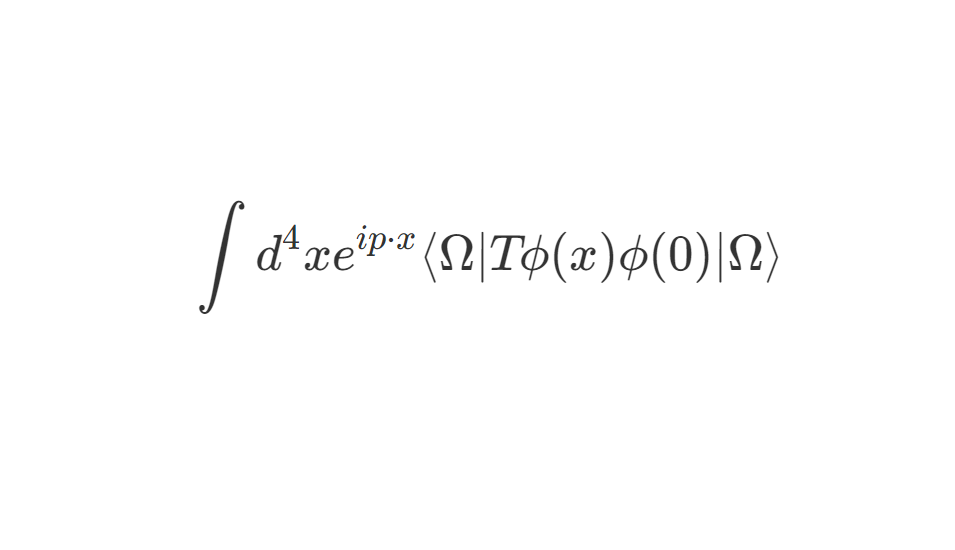拉格朗日场论

回顾：在经典力学中，作用量 S=∫LdtS = \int Ldt 描述了一个系统的状态。最小作用量原理 告诉我们：真实运动对应的作用量应当取极小值。根据最小作用量原理，我们可以导出系统的运动方程。
拉格朗日函数 LL 是一个关于广义坐标 qq，广义速度 q˙\dot{q}，时间 tt 的函数。

L=L(q,q˙,t)L = L(q,\dot{q},t)

最小做用量原理告诉我们，作用量的 等时变分 应当等于零：

0=δS=δ∫L(q,q˙,t)dt=∫(∂L∂qδq+∂L∂q˙δq˙)dt(1)\begin{aligned} 0 = \delta S &= \delta \int L(q,\dot{q},t)dt\\ &= \int (\frac{\partial L}{\partial q}\delta q + \frac{\partial L}{\partial \dot{q}}\delta {\dot{q}})dt\\ \end{aligned}\tag{1}

考虑到微分与变分可以交换，上式第二项可以写为：

∂L∂q˙δq˙dt=∂L∂q˙δdq=∂L∂q˙dδq=d(∂L∂q˙δq)−ddt(∂L∂q˙)δqdt\frac{\partial L}{\partial \dot{q}}\delta {\dot{q}}dt = \frac{\partial L}{\partial \dot{q}}\delta {dq} = \frac{\partial L}{\partial \dot{q}}d\delta {q} = d(\frac{\partial L}{\partial \dot{q}}\delta {q}) - \frac{d}{dt}(\frac{\partial L}{\partial \dot{q}})\delta {q}dt

于是 (1)(1) 式成为：

0=δS=∫(∂L∂q−ddt(∂L∂q˙))δqdt+∂L∂q˙δq∣(q0,q˙0,t0)(q1,q˙1,t1)=∫(∂L∂q−ddt(∂L∂q˙))δqdt(2)\begin{aligned} 0 = \delta S &= \int (\frac{\partial L}{\partial q} - \frac{d}{dt}(\frac{\partial L}{\partial \dot{q}}))\delta q dt + \frac{\partial L}{\partial \dot{q}}\delta {q} |_{(q_0,\dot{q}_0,t_0)}^{(q_1,\dot{q}_1,t_1)}\\ &= \int (\frac{\partial L}{\partial q} - \frac{d}{dt}(\frac{\partial L}{\partial \dot{q}}))\delta q dt \end{aligned}\tag{2}

其中 (q0,q˙0,t0)(q_0,\dot{q}_0,t_0) 与 (q1,q˙1,t1)(q_1,\dot{q}_1,t_1) 分别指初始位形与末态位形，因为变分 δq\delta q 只对中间的可能位形进行改变，而初态和末态是固定的，因此变分 δq\delta q 在初态和末态取值为零。

考虑变分 δq\delta q 可以任意选取，因此 (2)(2) 式为零实际上要求：

∂L∂q−ddt(∂L∂q˙)=0(3)\frac{\partial L}{\partial q} - \frac{d}{dt}(\frac{\partial L}{\partial \dot{q}}) = 0 \tag{3}

这就是 拉格朗日方程 Lagrange equation。它是我们通过最小作用量原理导出的运动方程。

在物理学中，我们引入了很多有关 场 的概念：如电场、磁场、引力场等。这些场都可以用一个依赖于位置 x\bm{x} 的物理量来进行描述。如电场，我们可以用电势 φ(x)\varphi(\bm{x}) 来描述。如果要研究场的运动，那么我们就要将原来只是描述质点或质点系的作用量、拉格朗日量等概念扩充到连续的场上去。

现在，我们使用拉格朗日量 LL 去描述一个连续的场 ϕ(x)\phi(\bm{x})。

拉格朗日量的可加性暗示我们可以引入拉格朗日量密度 L(x)\mathcal{L}(\bm{x})，将拉格朗日量写为：

L=∫d3xL(x)(4)L = \int d^3x \mathcal{L}(\bm{x}) \tag{4}

类比 LL 选取 q,q˙q,\dot{q} 为自由变量。场的拉格朗日密度 L(x)\mathcal{L}(\bm{x}) 选取 ϕ(x)\phi(\bm{x}) 及其导数 ∂μϕ(x)\partial_{\mu}\phi(\bm{x}) 为自由变量：

L(x)=L(ϕ(x),∂μϕ(x))(5)\mathcal{L}(\bm{x}) = \mathcal{L}(\phi(\bm{x}),\partial_{\mu}\phi(\bm{x})) \tag{5}

结合语境，我们常称 L\mathcal{L} 为拉格朗日量。

在 (5)(5) 式中，L(x)\mathcal{L}(\bm{x}) 只能依赖 ϕ,∂μϕ\phi,\partial_{\mu}\phi 在 x\bm{x} 点的取值。我们做以下说明：若 L(x)\mathcal{L}(\bm{x}) 依赖于 ϕ,∂μϕ\phi,\partial_{\mu}\phi 在某一点 y≠x\bm{y}\neq \bm{x} 的取值，那么在场在 y\bm{y} 点的取值变化将瞬时影响到 x\bm{x} 点，这显然不符合因果律。

作用量可以写为：

S=∫Ldt=∫L(ϕ,∂μϕ)d4x(6)S =\int Ldt =\int \mathcal{L}(\phi,\partial_{\mu}\phi)d^4x \tag{6}

根据 最小作用量原理，有：

0=δS=∫d4x{∂L∂ϕδϕ+∂L∂(∂μϕ)δ(∂μϕ)}=∫d4x{∂L∂ϕδϕ−∂μ(∂L∂(∂μϕ))δϕ+∂μ(∂L∂(∂μϕ)δϕ)}=∫d4x{[∂L∂ϕ−∂μ(∂L∂(∂μϕ))]δϕ}(7)\begin{aligned} 0 =\delta S &=\int d^4x \{\frac{\partial \mathcal{L}}{\partial \phi}\delta\phi+\frac{\partial \mathcal{L}}{\partial (\partial_{\mu}\phi)}\delta(\partial_{\mu}\phi) \}\\ &=\int d^4x \{\frac{\partial \mathcal{L}}{\partial \phi}\delta\phi-\partial_{\mu}(\frac{\partial \mathcal{L}}{\partial (\partial_{\mu}\phi)})\delta\phi + \partial_{\mu}(\frac{\partial \mathcal{L}}{\partial (\partial_{\mu}\phi)}\delta\phi)\}\\ &=\int d^4x \{[\frac{\partial \mathcal{L}}{\partial \phi}-\partial_{\mu}(\frac{\partial \mathcal{L}}{\partial (\partial_{\mu}\phi)})]\delta\phi \}\\ \end{aligned} \tag{7}

利用高斯公式：

∫d4x∂μ(∂L∂(∂μϕ)δϕ)=∫ΩdS∂L∂(∂μϕ)δϕ\int d^4x \partial_{\mu}(\frac{\partial \mathcal{L}}{\partial (\partial_{\mu}\phi)}\delta\phi) =\int_{\Omega} dS \frac{\partial \mathcal{L}}{\partial (\partial_{\mu}\phi)}\delta\phi

其中积分正是在初态与末态对应的世界面 Ω\Omega 上进行，而 δϕ∣Ω=0\delta \phi|_{\Omega} = 0，因此这一项为零。

得到场的 拉格朗日方程 为：

∂μ(∂L∂(∂μϕ))−∂L∂ϕ=0(8)\partial_{\mu}(\frac{\partial \mathcal{L}}{\partial (\partial_{\mu}\phi)})-\frac{\partial \mathcal{L}}{\partial \phi}=0 \tag{8}

哈密顿场论

回顾：哈密顿力学将广义坐标和广义动量置于平等的地位，由此给出的运动方程—— 哈密顿正则方程 正体现了这一点。不同于拉格朗日量，哈密顿量以广义坐标和广义动量为变量。于是，我们考虑对拉格朗日量进行 勒让德变换 以得到哈密顿量：

H(p,q,t)≡pq˙−L(q,q˙,t)(9)H(p,q,t) \equiv p\dot{q} - L(q,\dot{q},t) \tag{9}

其中广义动量 pp 定义为：

p≡∂L∂q˙(10)p\equiv \frac{\partial L}{\partial \dot{q}} \tag{10}

考虑哈密顿量的微分：

dH=dpq˙+pdq˙−∂L∂qdq−∂L∂q˙dq˙−∂L∂tdt=q˙dp+pdq˙−p˙dq−pdq˙−∂L∂tdt=q˙dp−p˙dq−∂L∂tdt(11)\begin{aligned} dH &= dp \dot{q} + pd\dot{q} - \frac{\partial L}{\partial q}dq - \frac{\partial L}{\partial \dot{q}}d\dot{q} - \frac{\partial L}{\partial t}dt\\ &= \dot{q}dp + pd\dot{q} - \dot{p}dq - pd\dot{q} -\frac{\partial L}{\partial t}dt\\ &= \dot{q}dp - \dot{p}dq -\frac{\partial L}{\partial t}dt\\ \end{aligned}\tag{11}

另一方面：

dH(p,q,t)=∂H∂pdp+∂H∂qdq+∂H∂tdt(12)dH(p,q,t) = \frac{\partial H}{\partial p}dp + \frac{\partial H}{\partial q}dq + \frac{\partial H}{\partial t}dt \tag{12}

结合 (11)(12)(11)(12) 得到 (13)(14)(13)(14)：

{∂H∂p=q˙∂H∂q=−p˙(13)\left\{ \begin{aligned} &\frac{\partial H}{\partial p} = \dot{q}\\ &\frac{\partial H}{\partial q} = -\dot{p}\\ \end{aligned}\right.\tag{13}

即哈密顿正则方程。以及：

∂H∂t=−∂L∂t(13)\frac{\partial H}{\partial t} = - \frac{\partial L}{\partial t} \tag{13}

另外由 (11)(11) 可得：

dHdt=q˙p˙−p˙q˙−∂L∂t=−∂L∂t(14)\frac{dH}{dt} = \dot{q}\dot{p} - \dot{p}\dot{q} - \frac{\partial L}{\partial t} = - \frac{\partial L}{\partial t} \tag{14}

由 (13)(14)(13)(14) 可以得到：

dHdt=∂H∂t(15)\frac{dH}{dt} = \frac{\partial H}{\partial t} \tag{15}

这实际上告诉我们若哈密顿量不含时，其成为一个守恒量。这点正与体系的能量所遵从的特点一致。

现在我们从拉格朗日场论出发，引入哈密顿场论。首先计算广义坐标 ϕ(x)\phi(\bm{x}) 对应的广义动量 p(x)p(\bm{x})：

p(x)=∂L∂ϕ˙(x)=∂∂ϕ˙(x)∫L(ϕ(y),∂μϕ(y))d3y∼∂∂ϕ˙(x)∑yL(ϕ(y),∂μϕ(y))d3y=π(x)d3x(16)\begin{aligned} p(\bm{x}) &= \frac{\partial L}{\partial \dot{\phi}(\bm{x})}\\ &= \frac{\partial }{\partial \dot{\phi}(\bm{x})}\int \mathcal{L}(\phi(\bm{y}),\partial_{\mu}\phi(\bm{y}))d^3 y\\ &\sim \frac{\partial }{\partial \dot{\phi}(\bm{x})}\sum_{\bm{y}} \mathcal{L}(\phi(\bm{y}),\partial_{\mu}\phi(\bm{y}))d^3 y = \pi(\bm{x})d^3x\\ \end{aligned}\tag{16}

其中 π(x)\pi(\bm{x}) 为与场量 ϕ(x)\phi(\bm{x}) 共轭的 动量密度：

π(x)≡∂L∂ϕ˙(x)(17)\pi(\bm{x}) \equiv \frac{\partial \mathcal{L}}{\partial \dot{\phi}(\bm{x})} \tag{17}

得到场的哈密顿量为：

H=∑xp(x)ϕ˙(x)−L=∫d3x(π(x)ϕ˙(x)−L)=∫d3xH(18)\begin{aligned} H &= \sum_{\bm{x}}p(\bm{x})\dot{\phi}(\bm{x}) - L\\ & = \int d^3x (\pi(\bm{x})\dot{\phi}(\bm{x}) - \mathcal{L} ) = \int d^3x \mathcal{H} \tag{18} \end{aligned}

其中 H\mathcal{H} 为场的哈密顿量密度，或简称为场的 哈密顿量：

H(ϕ,π)≡πϕ˙−L,π≡∂L∂ϕ˙(19)\mathcal{H}(\phi,\pi) \equiv \pi\dot{\phi} - \mathcal{L},\quad \pi \equiv \frac{\partial \mathcal{L}}{\partial \dot{\phi}}\tag{19}

读到这里，大家可能会有疑问：在拉格朗日场论中，我们为 L\mathcal{L} 选取的自由变量为 ϕ,∂μϕ\phi,\partial_{\mu}\phi，而在哈密顿场论中，我们却说 H\mathcal{H} 的自由变量为 ϕ,π\phi,\pi。可以看到 (19)(19) 式只进行了一个从 {ϕ,ϕ˙}\{\phi,\dot{\phi}\} 到 {ϕ,π}\{\phi,\pi\} 的勒让德变换。为什么不将哈密顿量定义为以下形式呢？

H′(ϕ,πμ)≡πμ∂μϕ−L,πμ≡∂L∂(∂μϕ)(20)\mathcal{H}'(\phi,\pi^{\mu}) \equiv \pi^{\mu}\partial_{\mu}\phi - \mathcal{L},\quad \pi^{\mu} \equiv \frac{\partial \mathcal{L}}{\partial (\partial_{\mu}\phi)} \tag{20}

首先说明：对于拉格朗日量，选取的自由变量为 ϕ,∂μϕ\phi,\partial_{\mu}\phi 的一个重要原因是：我们希望利用四导数去构造一个洛伦兹不变的拉格朗日量，对应的作用量与运动方程都是洛伦兹不变的。而对于哈密顿量来说，我们期望：

  1. 场量和动量的地位是平等的

  2. 与体系的能量相对应

在 (20)(20) 式中，场量 ϕ\phi 与动量 πμ\pi^{\mu} 的地位显然不等同（例如当 ϕ\phi 为标量场时，πμ\pi^{\mu} 为四矢量）。但是我们可以预期，由于 (19)(19) 式只进行了一个部分的勒让德变换，那么对应的哈密顿正则方程将在一定程度上被破坏。我们有：

dH=ϕ˙dπ+πdϕ˙−∂L∂ϕdϕ−∂L∂(∂μϕ)d(∂μϕ)=ϕ˙dπ+πdϕ˙−(∂μ∂L∂(∂μϕ))dϕ−πdϕ˙−∂L∂(∇ϕ)d(∇ϕ)=ϕ˙dπ−π˙dϕ−∇(∂L∂(∇ϕ))dϕ−∂L∂(∇ϕ)∇dϕ=ϕ˙dπ−π˙dϕ−∇(∂L∂(∇ϕ)dϕ)\begin{aligned} d\mathcal{H} &= \dot{\phi}d\pi + \pi d\dot{\phi} - \frac{\partial L}{\partial \phi}d\phi - \frac{\partial L}{\partial (\partial_{\mu} \phi) }d(\partial_{\mu}\phi)\\ &= \dot{\phi}d\pi + \pi d\dot{\phi} - (\partial_{\mu} \frac{\partial L}{\partial (\partial_{\mu} \phi) })d\phi - \pi d \dot{\phi} - \frac{\partial L}{\partial (\nabla \phi) }d(\nabla \phi)\\ &= \dot{\phi}d\pi - \dot{\pi}d\phi - \nabla (\frac{\partial L}{\partial (\nabla \phi) })d\phi- \frac{\partial L}{\partial (\nabla \phi) }\nabla d\phi\\ &= \dot{\phi}d\pi - \dot{\pi}d\phi - \nabla (\frac{\partial L}{\partial (\nabla \phi) }d\phi)\\ \end{aligned}

注意此时哈密顿正则方程并不成立。但我们发现：

dHdt=∫d3xdHdt=∫d3x(ϕ˙π˙−π˙ϕ˙)−ddt∫d3x∇(∂L∂(∇ϕ)dϕ)=−ddt∫dS∂L∂(∇ϕ)dϕ=0\begin{aligned} \frac{dH}{dt} &= \int d^3x \frac{d\mathcal{H}}{dt}\\ &= \int d^3x (\dot{\phi}\dot{\pi} - \dot{\pi}\dot{\phi}) - \frac{d}{dt}\int d^3x \nabla (\frac{\partial L}{\partial (\nabla \phi) }d\phi)\\ &= -\frac{d}{dt}\int dS \frac{\partial L}{\partial (\nabla \phi) }d\phi = 0\\ \end{aligned}

最后一步，我们考虑的情况是场局限在一有限趋于内，因此在无穷远边界处的面积分为零。此时，我们发现哈密顿量正是一个守恒量！这暗示我们如此定义的哈密顿量可以与体系的能量相对应。而根据 (20)(20) 式定义的 H′\mathcal{H}' 并不具有这个性质。

dH′=∂μϕdπμ+πμd∂μϕ−∂L∂ϕdϕ−∂L∂(∂μϕ)d(∂μϕ)=∂μϕdπμ+πμd∂μϕ−∂μπμdϕ−πμd(∂μϕ)=∂μϕdπμ−∂μπμdϕ\begin{aligned} d\mathcal{H}' &= \partial_{\mu}\phi d\pi^{\mu} + \pi^{\mu} d \partial_{\mu}\phi - \frac{\partial L}{\partial \phi}d\phi - \frac{\partial L}{\partial (\partial_{\mu} \phi) }d(\partial_{\mu}\phi)\\ &=\partial_{\mu}\phi d\pi^{\mu} + \pi^{\mu} d \partial_{\mu}\phi - \partial_{\mu}\pi^{\mu}d\phi - \pi^{\mu} d(\partial_{\mu}\phi)\\ &=\partial_{\mu}\phi d\pi^{\mu}-\partial_{\mu}\pi^{\mu}d\phi\\ \end{aligned}

虽然其有类似于哈密顿正则方程的如下方程：

{∂H′∂ϕ=−∂μπμ∂H′∂πμ=∂μϕ\left\{ \begin{aligned} & \frac{\partial \mathcal{H}'}{\partial \phi} = -\partial_{\mu}\pi^{\mu}\\ & \frac{\partial \mathcal{H}'}{\partial \pi^{\mu}} = \partial_{\mu}\phi\\ \end{aligned} \right.

但是 H′H' 并不是一个守恒量。

例：考虑具有如下拉格朗日量的场：

L=12ϕ˙2−12(∇ϕ)2−12m2ϕ2=12(∂μϕ)2−12m2ϕ2\begin{aligned} \mathcal{L}&=\frac{1}{2}\dot{\phi}^2 - \frac{1}{2}(\nabla\phi)^2 - \frac{1}{2}m^2\phi^2\\ &=\frac{1}{2}(\partial_{\mu}\phi)^2-\frac{1}{2}m^2\phi^2\\ \end{aligned}

考虑实值场的情形，mm 可以理解为质量。
对应的拉格朗日方程为：

(∂μ∂μ+m2)ϕ=0(\partial^{\mu}\partial_{\mu}+m^2)\phi = 0

这就是之后将要讨论的 Klein-Gordon 方程。
注意到：π(x)=ϕ˙(x)\pi(x) = \dot{\phi}(x)
哈密顿量为：

H=∫d3xH=∫d3x[12π2+12(∇ϕ)2+12m2ϕ2]H = \int d^3x \mathcal{H} = \int d^3x[\frac{1}{2}\pi^2 + \frac{1}{2}(\nabla\phi)^2 + \frac{1}{2}m^2\phi^2]

这三项可分别的物理含义为：

  • 场随时间运动的能量
  • 场随空间传播的能量
  • 场存在所固有的能量

Noether 定理

在理论力学中，Noether 定理揭示了守恒量与连续对称性的关系。现在来讨论场论中 Noether 定理的形式。

考虑对场做一无穷小变换：

ϕ(x)→ϕ(x)+αΔϕ(x)(21)\phi(\bm{x})\rightarrow \phi(\bm{x}) + \alpha \Delta \phi(\bm{x}) \tag{21}

如果在此变化下，拉格朗日量仅仅改变一表面项，对应的作用量是不变化的。如此，导出的运动方程也不变化。即：

L(x)→L(x)+α∂μJμ(x)(22)\mathcal{L}(\bm{x})\rightarrow \mathcal{L}(\bm{x}) + \alpha \partial_{\mu}\mathcal{J}^{\mu}(\bm{x}) \tag{22}

那么我们称这个变换为 对称变换。
可得拉格朗日量的变化为：

αΔL=∂L∂ϕ(αΔϕ)+∂L∂(∂μϕ)∂μ(αΔϕ)=α∂μ(∂L∂(∂μϕ)Δϕ)+αΔϕ(∂L∂ϕ−∂μ∂L∂(∂μϕ))=α∂μ(∂L∂(∂μϕ)Δϕ)(23)\begin{aligned} \alpha \Delta \mathcal{L} &= \frac{\partial \mathcal{L}}{\partial \phi}(\alpha\Delta\phi) + \frac{\partial \mathcal{L}}{\partial (\partial_{\mu} \phi)}\partial_{\mu}(\alpha\Delta\phi) \\ &= \alpha \partial_{\mu}(\frac{\partial \mathcal{L}}{\partial(\partial_{\mu} \phi)} \Delta\phi) + \alpha \Delta\phi (\frac{\partial \mathcal{L}}{\partial \phi}-\partial_{\mu}\frac{\partial \mathcal{L}}{\partial (\partial_{\mu} \phi)}) \\ & = \alpha\partial_{\mu}( \frac{\partial \mathcal{L}}{\partial (\partial_{\mu} \phi)}\Delta\phi) \end{aligned}\tag{23}

若该变换为对称变换，则变换前后的运动方程不会改变。由此拉格朗日量至多相差一个全微分项。考虑 (22)(23)(22)(23)，得到：

α∂μJμ(x)=α∂μ[∂L∂(∂μϕ)Δϕ]\alpha\partial_{\mu} \mathcal{J}^{\mu}(x) = \alpha\partial_{\mu}[ \frac{\partial \mathcal{L}}{\partial (\partial_{\mu} \phi)}\Delta\phi]

可以写为：

∂μjμ=0jμ≡∂L∂(∂μϕ)Δϕ−Jμ(x)(24)\partial_{\mu} j^{\mu} = 0\quad j^{\mu} \equiv \frac{\partial \mathcal{L}}{\partial (\partial_{\mu} \phi)}\Delta\phi-\mathcal{J}^{\mu}(x) \tag{24}

如此四维流 jμ(x)j^{\mu}(\bm{x}) 是守恒的。得到守恒流方程：

∂j0∂t+∇⋅j=0(25)\frac{\partial j^0}{\partial t} + \nabla\cdot \bm{j} = 0 \tag{25}

得到：

∂∂t∫j0d3x=−∫V∇⋅jd3x=−∫Sj⋅dS\begin{aligned} \frac{\partial}{\partial t}\int j^0d^3x &= -\int_V \nabla\cdot\bm{j} d^3x\\ &= -\int_S \bm{j}\cdot d\bm{S}\\ \end{aligned}

取积分域为全空间，得到上式右边应当趋于零。得到守恒流对应的守恒荷：

Q≡∫all spacej0d3x(26)Q \equiv \int_{all\ space} j^0 d^3x \tag{26}

现在我们考虑一些对称变换和对应的守恒量。

  1. 对复值量 ϕ\phi 相位 的变化：ϕ→eiαϕ\phi \rightarrow e^{i\alpha}\phi
    我们首先将实值场拓展到复值场的情形，此时拉格朗日量为：

L=∣∂μϕ∣2−m2ϕ2=∂μϕ∗∂μϕ−m2ϕ∗ϕ\begin{aligned} \mathcal{L} &= |\partial_{\mu}\phi|^2-m^2\phi^2\\ &= \partial^{\mu} \phi^*\partial_{\mu} \phi - m^2\phi^*\phi\\ \end{aligned}

该拉氏量在相位变换下并不发生改变。因此 Jμ=0\mathcal{J}^{\mu}=0。
又有：

ϕ→ϕ′=ϕ+iαϕ⇒Δϕ=iϕϕ∗→ϕ∗′=ϕ∗−iαϕ∗⇒Δϕ∗=−iϕ∗\begin{aligned} &\phi \rightarrow \phi' = \phi + i\alpha \phi \Rightarrow \Delta \phi = i\phi \\ &\phi^* \rightarrow \phi^{*'} = \phi^* - i\alpha \phi^{*} \Rightarrow \Delta \phi^* = -i\phi^*\\ \end{aligned}

我们将 ϕ,ϕ∗\phi,\phi^* 看作独立变量。

根据 Noether 定理，得到守恒流为：

jμ=i[(∂μϕ∗)ϕ−ϕ∗(∂μϕ)]j^{\mu} = i[(\partial^{\mu}\phi^{*})\phi-\phi^* (\partial^{\mu}\phi) ]

对应的守恒荷为：

Q=∫d3j0=∫d3xi(ϕ˙∗ϕ−ϕ∗ϕ˙)Q = \int d^3 j^0 = \int d^3x i(\dot{\phi}^*\phi - \phi^*\dot{\phi})

对于考虑电磁耦合的拉氏量，我们发现这一项正是电荷。这是拉氏量具有 U(1)U(1) 对称性所对应的守恒量。

  1. 考虑平移：xμ→xμ−aμx^{\mu} \rightarrow x^{\mu} - a^{\mu}
    场量将进行以下变换：

ϕ(x)→ϕ(x+a)=ϕ(x)+aμ∂μϕ(x)⇒Δϕ=aμ∂μϕ\phi(x) \rightarrow \phi(x+a) = \phi(x) + a^{\mu}\partial_{\mu} \phi(x) \Rightarrow \Delta\phi = a^{\mu}\partial_{\mu}\phi

由于拉格朗日量是标量，也应该遵循相同的变换方式：

L→L+aμ∂μL=L+aν∂μ(δ  νμL)\mathcal{L}\rightarrow \mathcal{L} + a^{\mu}\partial_{\mu}\mathcal{L} = \mathcal{L} + a^{\nu}\partial_{\mu}(\delta^{\mu}_{\ \ \nu}\mathcal{L})

可以得到如下守恒量：

jμ=∂L∂(∂μϕ)aν∂νϕ−aνδ  νμL=aν(∂L∂(∂μϕ)∂νϕ−Lδ  νμ)\begin{aligned} j^{\mu} &= \frac{\partial \mathcal{L}}{\partial (\partial_{\mu}\phi)} a^{\nu}\partial_{\nu}\phi - a^{\nu}\delta^{\mu}_{\ \ \nu}\mathcal{L}\\ &= a^{\nu} (\frac{\partial \mathcal{L}}{\partial (\partial_{\mu}\phi)}\partial_{\nu}\phi - \mathcal{L}\delta^{\mu}_{\ \ \nu})\\ \end{aligned}

考虑到 aνa^{\nu} 可以随意选取。可得如下守恒张量：

T  νμ≡∂L∂(∂μϕ)∂νϕ−Lδ  νμ(27)T^{\mu}_{\ \ \nu} \equiv \frac{\partial \mathcal{L}}{\partial (\partial_{\mu}\phi)}\partial_{\nu}\phi - \mathcal{L}\delta^{\mu}_{\ \ \nu} \tag{27}

这个张量被称为 能量-动量张量。又可以写为：

Tμν≡T  ρμgρν=∂L∂(∂μϕ)∂νϕ−Lgμν(28)T^{\mu\nu} \equiv T^{\mu}_{\ \ \rho}g^{\rho\nu} = \frac{\partial \mathcal{L}}{\partial (\partial_{\mu}\phi)}\partial^{\nu}\phi - \mathcal{L}g^{\mu\nu} \tag{28}

我们现在考虑这个张量的性质。指出 ν=0\nu = 0 对应守恒荷，μ=0\mu = 0 对应时间平移，μ≠0\mu \neq 0 对应空间平移。

可得时间平移和空间平移对应的守恒荷为：

∫T00d3x=∫(πϕ˙−L)d3x=∫Hd3x=H∫T0id3x=−∫π∂iϕd3x≡Pi(29)\begin{aligned} &\int T^{00} d^3x = \int (\pi \dot{\phi}- \mathcal{L})d^3x= \int\mathcal{H}d^3x = H\\ &\int T^{0i} d^3x = -\int\pi\partial_i\phi d^3x \equiv P^{i}\\ \end{aligned}\tag{29}

以上第一式给出了系统的能量，这与时间平移相关。我们定义与空间平移相关的第二式就为系统的 物理动量。

一般来说，TμνT^{\mu\nu} 并不是一个对称张量。若 TμνT^{\mu\nu} 为一个对称张量，那么系统的角动量守恒。