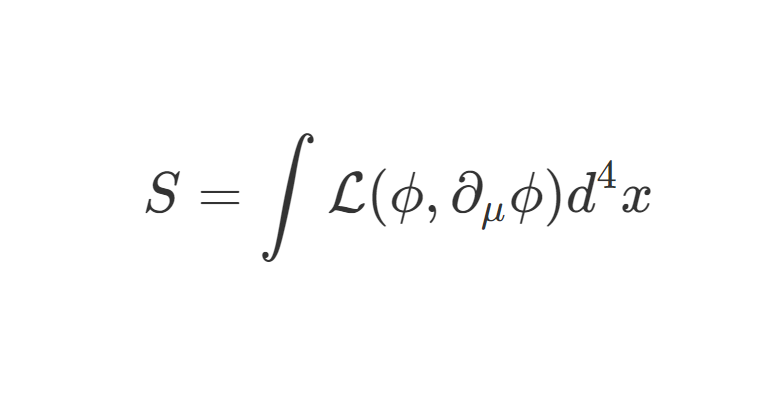Klein-Gordon 方程

Klein-Gordon 方程是相对论量子力学中最基本的方程之一。现在我们遵循“一次量子化程式”，从相对论质能关系出发，对 Klein-Gordon 方程给出形式的推导：

注意在量子场论中，我们一般采用自然单位制，即 ℏ=c=1\hbar = c =1

相对论质能关系为

E2=m2+p2(1)E^2 = m^2 + p^2 \tag{1}

将物理量使用算子代替，并且在坐标表象中有：

{E→E^=i∂∂tm→m^=mp→p^=−i∇(2)\left\{ \begin{aligned} &E \rightarrow \hat{E} = i\frac{\partial}{\partial t}\\ &m \rightarrow \hat{m} = m\\ &p \rightarrow \hat{p} = -i\nabla\\ \end{aligned} \right.\tag{2}

即将 c-number (classcial number) 用对应的 q-number (quantum number) 代替，即一次量子化。

得到 Klein-Gordon 方程为：

−∂2ϕ∂t2=(m2−∇2)ϕ-\frac{\partial^2 \phi}{\partial t^2} = (m^2-\nabla^2)\phi

利用四导数 ∂μ\partial_{\mu} 写为：

(∂μ∂μ+m2)ϕ=0(3)(\partial_{\mu}\partial^{\mu} + m^2)\phi = 0 \tag{3}

四导数定义为：

∂μ=(∂0,∂1,∂2,∂3)∂μ=(∂0,−∂1,−∂2,−∂3)\begin{aligned} \partial_{\mu} &= (\partial_0,\partial_1,\partial_2,\partial_3)\\ \partial^{\mu} &= (\partial_0,-\partial_1,-\partial_2,-\partial_3)\\ \end{aligned}

虽然在相对论量子力学中，Klein-Gordon 方程存在很多问题：如负能解与负几率，它并不是一个自洽的方程。但之后我们将会看到，在场论中，Klein-Gordon 方程可以用来描述自旋为零的玻色子场。Klein-Gordon 方程所对应的拉格朗日量为：

L=12∂μϕ∂μϕ−12m2ϕ2(4)L = \frac{1}{2}\partial_{\mu}\phi\partial^{\mu}\phi - \frac{1}{2}m^2\phi^2 \tag{4}

Klein-Gordon 场的量子化

满足 Klein-Gordon 方程 的 实值场 ϕ(x,t)\phi(\bm{x},t) 称为 Klein-Gordon 场。为了将 Klein-Gordon 场量子化，我们首先回顾对经典谐振子进行量子化的方法。

普朗克振子

经典谐振子的哈密顿量具有以下形式：

H=p22m+12mω2x2(5)H = \frac{p^2}{2m} + \frac{1}{2}m\omega^2x^2 \tag{5}

将 c-number 替换为 q-number，并根据对易关系进行一次量子化：

H^=p^22m+12mω2x^2,[x^,p^]=i(6)\hat{H} = \frac{\hat{p}^2}{2m} + \frac{1}{2}m\omega^2\hat{x}^2,\quad [\hat{x},\hat{p}] = i \tag{6}

我们将量子化后的简谐振子称为 普朗克振子 Planck oscillator。引入 阶梯算子 ladder operator：

{a^=p^2mω−imω2x^a^†=p^2mω+imω2x^(7)\left\{ \begin{aligned} &\hat{a} = \frac{\hat{p}}{\sqrt{2m\omega}} - i\sqrt{\frac{m\omega}{2}} \hat{x}\\ &\hat{a}^\dagger = \frac{\hat{p}}{\sqrt{2m\omega}} + i\sqrt{\frac{m\omega}{2}} \hat{x}\\ \end{aligned}\tag{7} \right.

a^\hat{a} 称为 湮灭算子 annihilation operator，a^†\hat{a}^\dagger 称为 产生算子 creation operator。我们将在本篇末理解此处命名的含义。

狄拉克引入阶梯算子，是基于以下考虑：对于 c-number 组成的哈密顿量，我们可以进行因式分解：

H=p22m−(−12mω2x2)=(p2m)2−(−im2ωx)2=ω(1ω)2(p2m−im2ωx)(p2m+im2ωx)=ω(p2mω−imω2x)(p2mω+imω2x)\begin{aligned} H &= \frac{p^2}{2m} - (-\frac{1}{2}m\omega^2x^2)\\ &= (\frac{p}{\sqrt{2m}})^2 - (-i\sqrt{\frac{m}{2}}\omega x)^2\\ &= \omega(\frac{1}{\sqrt{\omega}})^2(\frac{p}{\sqrt{2m}} - i\sqrt{\frac{m}{2}}\omega x)(\frac{p}{\sqrt{2m}} + i\sqrt{\frac{m}{2}}\omega x)\\ &= \omega(\frac{p}{\sqrt{2m\omega}} - i\sqrt{\frac{m\omega}{2}} x)(\frac{p}{\sqrt{2m\omega}} + i\sqrt{\frac{m\omega}{2}} x)\\ \end{aligned}

然后将坐标算子和动量算子进行线性组合成阶梯算子。

利用 (7)(7) 式将坐标算子与动量算子使用阶梯算子表示：

{x^=12mω(a^+a^†)p^=−imω2(a^−a^†)(8)\left\{ \begin{aligned} & \hat{x} = \frac{1}{\sqrt{2m\omega}} (\hat{a} + \hat{a}^\dagger)\\ & \hat{p} = -i\sqrt{\frac{m\omega}{2}}(\hat{a} - \hat{a}^\dagger) \end{aligned}\tag{8} \right.

那么对易关系成为：

i=[x^,p^]=−i2[a^+a^†,a^−a^†]=i[a^,a^†]⇔[a^,a^†]=1(9)i = [\hat{x},\hat{p}] = -\frac{i}{2}[\hat{a}+\hat{a}^\dagger,\hat{a}-\hat{a}^\dagger] = i[\hat{a},\hat{a}^\dagger] \Leftrightarrow [\hat{a},\hat{a}^\dagger] = 1\tag{9}

这里实际上说明，对易关系 [x^,p^]=i[\hat{x},\hat{p}] = i 与 [a^,a^†]=1[\hat{a},\hat{a}^\dagger] = 1 是等价的，这提示我们，第二式也能作为量子化的出发点。

使用阶梯算子将哈密顿量写为：

H^=−ω4(a^−a^†)2+ω4(a^+a^†)2=ω2(a^a^†+a^†a^)=ω(a^†a^+12[a^,a^†])=ω(a^†a^+12)(10)\begin{aligned} \hat{H} &= -\frac{\omega}{4}(\hat{a}-\hat{a}^\dagger)^2 + \frac{\omega}{4}(\hat{a}+\hat{a}^\dagger)^2\\ &= \frac{\omega}{2}(\hat{a}\hat{a}^\dagger+\hat{a}^\dagger\hat{a})\\ &= \omega(\hat{a}^\dagger\hat{a} + \frac{1}{2} [\hat{a},\hat{a}^\dagger])\\ &= \omega(\hat{a}^\dagger\hat{a} + \frac{1}{2})\\ \end{aligned}\tag{10}

我们现在来求解普朗克振子的本征值问题。

首先来看 n^≡a^†a^\hat{n} \equiv \hat{a}^\dagger\hat{a}，它是厄密算子，其本征值为实数。其与阶梯算子的对易关系容易计算：

[n^,a^]=−a^[n^,a^†]=a^†(11)[\hat{n},\hat{a}] = -\hat{a}\quad [\hat{n},\hat{a}^\dagger] = \hat{a}^\dagger \tag{11}

假定 ∣λ⟩|\lambda\rangle 为 n^\hat{n} 的本征值为 λ\lambda 的本征态，即：

n^∣λ⟩=λ∣λ⟩\hat{n}|\lambda\rangle = \lambda |\lambda\rangle

可以得到：

n^a^†∣λ⟩=(a^†n^+[n^,a†])∣λ⟩=(λ+1)a^†∣λ⟩n^a^∣λ⟩=(a^n^+[n^,a])∣λ⟩=(λ−1)a^∣λ⟩(12)\begin{aligned} \hat{n}\hat{a}^\dagger|\lambda\rangle &= (\hat{a}^\dagger\hat{n} + [\hat{n},a^\dagger])|\lambda\rangle\\ &= (\lambda+1) \hat{a}^\dagger|\lambda\rangle\\ \hat{n}\hat{a}|\lambda\rangle &= (\hat{a}\hat{n} + [\hat{n},a])|\lambda\rangle\\ &= (\lambda-1) \hat{a}|\lambda\rangle\tag{12} \end{aligned}

因此 a†∣λ⟩a^\dagger|\lambda\rangle 为 n^\hat{n} 的本征值为 λ+1\lambda+1 的本征态，a∣λ⟩a|\lambda\rangle 为 n^\hat{n} 的本征值为 λ−1\lambda-1 的本征态，有:

a†∣λ⟩=c+,λ∣λ+1⟩,a∣λ⟩=c−,λ∣λ−1⟩a^\dagger|\lambda\rangle = c_{+,\lambda}|\lambda+1\rangle,\quad a|\lambda\rangle = c_{-,\lambda}|\lambda-1\rangle

计算因子 c±,λc_{\pm,\lambda}：

⟨λ∣a^a^†∣λ⟩=⟨λ∣c+,λ∗c+,λ∣λ⟩=∣c+,λ∣2⟨λ∣a^a^†∣λ⟩=⟨λ∣n^∣λ⟩=λ\begin{aligned} &\langle \lambda|\hat{a}\hat{a}^\dagger|\lambda\rangle = \langle \lambda|c_{+,\lambda}^*c_{+,\lambda}|\lambda\rangle = |c_{+,\lambda}|^2\\ &\langle \lambda|\hat{a}\hat{a}^\dagger|\lambda\rangle = \langle \lambda|\hat{n}|\lambda\rangle =\lambda \end{aligned}

此处可以得到本征值 λ⩾0\lambda \geqslant 0，可以取：

c+,λ=λc_{+,\lambda} = \sqrt{\lambda}

同理有：

c−,λ=λ−1c_{-,\lambda} = \sqrt{\lambda-1}

由于本征值大于等于零，而每次 a^\hat{a} 作用到 ∣λ⟩|\lambda\rangle 上得到本征值减一的本征态。那么可以得到 λ\lambda 应当只能取非负整数，我们于是将本征态为 ∣n⟩|n\rangle。且有：

a^∣0⟩=0\hat{a}|0\rangle = 0

∣0⟩|0\rangle 称为 基态 或 真空态。
综上，我们得到任意本征态：

∣n⟩=1n−1a†∣n−1⟩=1(n−1)!(a†)n∣0⟩|n\rangle = \frac{1}{\sqrt{n-1}}a^\dagger|n-1\rangle = \frac{1}{\sqrt{(n-1)!}}(a^\dagger)^n|0\rangle

Klein-Gordon 场的量子化

Klein-Gordon 场 ϕ(x,t)\phi(\bm{x},t) 满足方程：

−∂2∂t2ϕ(x,t)=(m2−∇2)ϕ(x,t)(13)-\frac{\partial^2}{\partial t^2}\phi(\bm{x},t) = (m^2-\nabla^2)\phi(\bm{x},t) \tag{13}

此处特别标注 ϕ\phi 的自变量为 x\bm{x}，表示其在坐标空间内取值。本质上说我们是在坐标表象下写出方程 (13)(13)，而 ϕ(x,t)=⟨x∣ϕ(t)⟩\phi(\bm{x},t) = \langle \bm{x}|\phi(t)\rangle。

ϕ\phi 为实值场要求：

ϕ(x,t)=ϕ∗(x,t)(14)\phi(\bm{x},t) = \phi^*(\bm{x},t) \tag{14}

现在我们期望在动量表象中重写 Klein-Gordon 方程，首先波函数可以写为：

ϕ(x,t)=⟨x∣ϕ(t)⟩=∫d3p(2π)3⟨x∣p⟩⟨p∣ϕ(t)⟩=∫d3p(2π)3eip⋅xϕ(p,t)(15)\begin{aligned} \phi(\bm{x},t) &= \langle \bm{x}|\phi(t)\rangle = \int \frac{d^3p}{(2\pi)^3} \langle \bm{x}|\bm{p}\rangle \langle \bm{p}|\phi(t)\rangle\\ &= \int \frac{d^3p}{(2\pi)^3} e^{i\bm{p}\cdot\bm{x}}\phi(\bm{p},t)\\ \end{aligned}\tag{15}

其中 ϕ(p,t)\phi(\bm{p},t) 就是动量表象下的波函数。式 (15)(15) 在形式上看就是一个傅里叶变换。此处 ϕ(x,t)\phi(\bm{x},t) 为实值场等价要求：

ϕ∗(p,t)=ϕ(−p,t)(16)\phi^*(\bm{p},t) = \phi(-\bm{p},t)\tag{16}

ϕ∗(x,t)=∫d3p(2π)3e−ip⋅xϕ∗(p,t)=∫d3p(2π)3eip⋅xϕ∗(−p,t)ϕ(x,t)=∫d3p(2π)3eip⋅xϕ(p,t)⇒ϕ∗(p,t)=ϕ(−p,t)\begin{aligned} \phi^*(\bm{x},t) &= \int \frac{d^3p}{(2\pi)^3} e^{-i\bm{p}\cdot\bm{x}}\phi^*(\bm{p},t)\\ &= \int \frac{d^3p}{(2\pi)^3} e^{i\bm{p}\cdot\bm{x}}\phi^*(-\bm{p},t)\\ \phi(\bm{x},t)&= \int \frac{d^3p}{(2\pi)^3} e^{i\bm{p}\cdot\bm{x}}\phi(\bm{p},t)\\ \Rightarrow & \phi^*(\bm{p},t) = \phi(-\bm{p},t) \end{aligned}

将 (15)(15) 式代入 (13)(13)，由此动量表象中的 Klein-Gordon 方程成为：

[∂2∂t2+(∣p∣2+m2)]ϕ(p,t)=0(17)[\frac{\partial^2}{\partial t^2} + (|\bm{p}|^2+m^2)] \phi(\bm{p},t) = 0 \tag{17}

上述方程与一个频率为 ωp=∣p∣2+m2\omega_{\bm{p}} = \sqrt{|\bm{p}|^2 + m^2} 的简谐振子的振动方程形式一样。对应的哈密顿量为：

Hp=12π2(p,t)+12ωp2ϕ2(p,t),π=∂ϕ∂t(18)H_{\bm{p}} = \frac{1}{2}\pi^2(\bm{p},t) + \frac{1}{2}\omega_{\bm{p}}^2\phi^2(\bm{p},t), \quad \pi = \frac{\partial \phi}{\partial t} \tag{18}

回忆我们处理简谐振子进行量子化的方法，通过引入阶梯算子，我们可以很轻松的计算谐振子的本征态与能级。现在，我们也想对上述问题应用相同的技巧。不过我们现在有一点疑问需要说明：我们明确我们所讨论问题的 绘景 picture。我们现在一直在 薛定谔绘景 Schrödinger picture 讨论问题：即认为算子不变，而波函数进行演化。在对简谐振子量子化的式 (6)(6) 中，我们将物理量直接用算子代替。而在 (17)(17) 式中，物理量 π,ϕ\pi,\phi 却是一个随时间演化的量！在这里，我们的做法是：只在一个固定的时刻论问题，因此 π,ϕ\pi,\phi 只是一个取值在特定时间的物理量。也就是说，现在我们已经能在固定时间对 (17)(17) 进行量子化了，下一篇我们能看到，如果要给出场的演化信息，必须要换到 海森堡绘景 Heisenberg 中进行讨论。

类比 (8)(8) 式，引入阶梯算子：

{ϕ^(p)=12ωp(a^p+a^−p†)π^(p)=−iωp2(a^p−a^−p†)(19)\left\{ \begin{aligned} \hat{\phi}(\bm{p}) &= \frac{1}{\sqrt{2\omega_{\bm{p}}}}(\hat{a}_{\bm{p}}+\hat{a}^\dagger_{-\bm{p}})\\ \hat{\pi}(\bm{p}) &= -i\sqrt{\frac{\omega_{\bm{p}}}{2}}(\hat{a}_{\bm{p}}-\hat{a}^\dagger_{-\bm{p}})\\ \end{aligned}\tag{19} \right.

注意为了保证 ϕ(x,t)\phi(\bm{x},t) 为实值场，条件 (16)(16) 需要满足，因此我们为阶梯算子标上不同的下标。

坐标表象中的场量和动量可以表示为：

ϕ^(x)=∫d3p(2π)312ωp(a^p+a^−p†)eip⋅x=∫d3p(2π)312ωp(a^peip⋅x+a^p†e−ip⋅x)π^(x)=∫d3p(2π)3(−i)ωp2(a^p−a^−p†)eip⋅x=∫d3p(2π)3(−i)ωp2(a^peip⋅x−a^p†e−ip⋅x)(20)\begin{aligned} \hat{\phi}(\bm{x}) &= \int \frac{d^3p}{(2\pi)^3} \frac{1}{\sqrt{2\omega_{\bm{p}}}}(\hat{a}_{\bm{p}}+\hat{a}_{-\bm{p}}^\dagger)e^{i\bm{p}\cdot\bm{x}}\\ &= \int \frac{d^3p}{(2\pi)^3} \frac{1}{\sqrt{2\omega_{\bm{p}}}}(\hat{a}_{\bm{p}}e^{i\bm{p}\cdot\bm{x}}+\hat{a}_{\bm{p}}^\dagger e^{-i\bm{p}\cdot\bm{x}}) \\ \hat{\pi}(\bm{x}) &= \int \frac{d^3p}{(2\pi)^3} (-i)\sqrt{\frac{\omega_{\bm{p}}}{2}}(\hat{a}_{\bm{p}}-\hat{a}_{-\bm{p}}^\dagger)e^{i\bm{p}\cdot\bm{x}}\\ &= \int \frac{d^3p}{(2\pi)^3} (-i)\sqrt{\frac{\omega_{\bm{p}}}{2}}(\hat{a}_{\bm{p}}e^{i\bm{p}\cdot\bm{x}}-\hat{a}_{\bm{p}}^\dagger e^{-i\bm{p}\cdot\bm{x}}) \\ \end{aligned}\tag{20}

上式子中的含有 eip⋅xe^{i\bm{p}\cdot\bm{x}} 与 e−ip⋅xe^{-i\bm{p}\cdot\bm{x}} 的项称为 正频项 positive frequency 与 负频项 negative frequency。

现在我们需要引入对易关系，作为对 Klein-Gordon 场量子化的出发点。根据 (9)(9) 式，我们给定阶梯算子的对易关系作为量子化条件

首先我们有基本的观察：

  1. [a^p,a^q]=[a^p†,a^q†]=0[\hat{a}_{\bm{p}},\hat{a}_{\bm{q}}] = [\hat{a}^\dagger_{\bm{p}},\hat{a}^\dagger_{\bm{q}}] = 0

  2. [a^p,a^q†]=0,∀ p≠q[\hat{a}_{\bm{p}},\hat{a}^\dagger_{\bm{q}}] =0 ,\forall\ \bm{p}\neq \bm{q}

只有形如 [ap,ap†][a_{\bm{p}},a_{\bm{p}}^\dagger] 的项才不为零。这提示我们可以采用下式作为量子化条件：

[a^p,a^q†]=(2π)3δ(3)(p−q)(21)[\hat{a}_{\bm{p}},\hat{a}^\dagger_{\bm{q}}] = (2\pi)^3\delta^{(3)}(\bm{p}-\bm{q}) \tag{21}

利用 (19)(19) 可得：

[ϕ^(p),π^(q)]=−iωq4ωp[a^p+a^−p†,a^q−a^−q†]=−iωq4ωp(−[a^p,a^−q†]+[a^−p†,a^q])=(2π)3iδ(3)(p+q)(22)\begin{aligned} [\hat{\phi}(\bm{p}),\hat{\pi}(\bm{q})] &= -i\sqrt{\frac{\omega_{\bm{q}}}{4\omega_{\bm{p}}}} [\hat{a}_{\bm{p}}+\hat{a}^\dagger_{-\bm{p}},\hat{a}_{\bm{q}}-\hat{a}^\dagger_{-\bm{q}}]\\ &= -i\sqrt{\frac{\omega_{\bm{q}}}{4\omega_{\bm{p}}}} (-[\hat{a}_{\bm{p}},\hat{a}^\dagger_{-\bm{q}}]+[\hat{a}^\dagger_{-\bm{p}},\hat{a}_{\bm{q}}])\\ &= (2\pi)^3i\delta^{(3)}(\bm{p}+\bm{q})\\ \end{aligned} \tag{22}

由此：

[ϕ^(x),π^(y)]=∫d3pd3q(2π)6ei(p⋅x+q⋅y)[ϕ^(p),π^(q)]=∫d3pd3q(2π)6ei(p⋅x+q⋅y)(2π)3iδ(3)(p+q)=i∫d3p(2π)3eip⋅(x−y)=iδ(3)(x−y)(23)\begin{aligned} [\hat{\phi}(\bm{x}),\hat{\pi}(\bm{y})] &= \int \frac{d^3pd^3q}{(2\pi)^6}e^{i(\bm{p}\cdot\bm{x}+\bm{q}\cdot\bm{y})}[\hat{\phi}(\bm{p}),\hat{\pi}(\bm{q})]\\ &= \int \frac{d^3pd^3q}{(2\pi)^6}e^{i(\bm{p}\cdot\bm{x}+\bm{q}\cdot\bm{y})}(2\pi)^3i\delta^{(3)}(\bm{p}+\bm{q})\\ &= i\int \frac{d^3p}{(2\pi)^3}e^{i\bm{p}\cdot(\bm{x}-\bm{y})}\\ &=i\delta^{(3)}(\bm{x}-\bm{y})\\ \end{aligned}\tag{23}

这正是对易关系 [x^,p^]=i[\hat{x},\hat{p}] = i 在场论中的推广！到这里，我们已经完成了对 Klein-Gordon 场进行量子化的过程。

哈密顿量、动量的对角化

现在我们希望用阶梯算子去表示体系的哈密顿量与动量，这称为算子的 对角化 过程。

我们先对哈密顿量进行对角化。Klein-Gordon 场的哈密顿量为：

H(x)=12π2+12(∇ϕ)2+12m2ϕ2(24)\mathcal{H}(\bm{x}) = \frac{1}{2}\pi^2 + \frac{1}{2}(\nabla\phi)^2 + \frac{1}{2}m^2\phi^2\tag{24}

得到：

H^=∫d3xH^=∫d3x[12π^2+12(∇ϕ^)2+12m2ϕ^2]=∫d3x∫d3pd3q(2π)6ei(p+q)⋅x{−ωpωq4(a^p−a^−p†)(a^q−a^−q†)+−p⋅q+m24ωpωq(a^p+a^−p†)(a^q+a^−q†)}=∫d3pd3q(2π)3δ(3)(p+q)ei(p+q)⋅x{−ωpωq4(a^p−a^−p†)(a^q−a^−q†)+−p⋅q+m24ωpωq(a^p+a^−p†)(a^q+a^−q†)}=∫d3p(2π)3{−ωp2(a^p−a^−p†)(a^q−a^−q†)+ωp2(a^p+a^−p†)(a^q+a^−q†)}=∫d3p(2π)3ωp2(a^pa^p†+a^−p†a^−p)=∫d3p(2π)3ωp2(a^pa^p†+a^p†a^p)=∫d3p(2π)3ωp(a^p†a^p+12[a^p,a^p†])\begin{aligned} \hat{H} &= \int d^3x \mathcal{\hat{H}} \\ &= \int d^3x[\frac{1}{2}\hat{\pi}^2 + \frac{1}{2}(\nabla\hat{\phi})^2 + \frac{1}{2}m^2\hat{\phi}^2] \\ &=\int d^3x \int \frac{d^3pd^3q}{(2\pi)^6}e^{i(\bm{p}+\bm{q})\cdot\bm{x}} \{-\frac{\sqrt{\omega_{\bm{p}}\omega_{\bm{q}}}}{4}(\hat{a}_{\bm{p}}-\hat{a}^\dagger_{-\bm{p}})(\hat{a}_{\bm{q}}-\hat{a}^\dagger_{-\bm{q}}) + \frac{-\bm{p}\cdot\bm{q}+m^2}{4\sqrt{\omega_{\bm{p}}\omega_{\bm{q}}}} (\hat{a}_{\bm{p}}+\hat{a}^\dagger_{-\bm{p}})(\hat{a}_{\bm{q}}+\hat{a}^\dagger_{-\bm{q}}) \}\\ &=\int \frac{d^3pd^3q}{(2\pi)^3}\delta^{(3)}(\bm{p}+\bm{q})e^{i(\bm{p}+\bm{q})\cdot\bm{x}} \{-\frac{\sqrt{\omega_{\bm{p}}\omega_{\bm{q}}}}{4}(\hat{a}_{\bm{p}}-\hat{a}^\dagger_{-\bm{p}})(\hat{a}_{\bm{q}}-\hat{a}^\dagger_{-\bm{q}}) + \frac{-\bm{p}\cdot\bm{q}+m^2}{4\sqrt{\omega_{\bm{p}}\omega_{\bm{q}}}} (\hat{a}_{\bm{p}}+\hat{a}^\dagger_{-\bm{p}})(\hat{a}_{\bm{q}}+\hat{a}^\dagger_{-\bm{q}}) \}\\ &=\int \frac{d^3p}{(2\pi)^3}\{-\frac{\omega_{\bm{p}}}{2}(\hat{a}_{\bm{p}}-\hat{a}^\dagger_{-\bm{p}})(\hat{a}_{\bm{q}}-\hat{a}^\dagger_{-\bm{q}}) + \frac{\omega_{\bm{p}}}{2} (\hat{a}_{\bm{p}}+\hat{a}^\dagger_{-\bm{p}})(\hat{a}_{\bm{q}}+\hat{a}^\dagger_{-\bm{q}}) \}\\ &=\int \frac{d^3p}{(2\pi)^3} \frac{\omega_{\bm{p}}}{2} (\hat{a}_{\bm{p}}\hat{a}^\dagger_{\bm{p}}+\hat{a}^\dagger_{-\bm{p}}\hat{a}_{-\bm{p}})\\ &=\int \frac{d^3p}{(2\pi)^3} \frac{\omega_{\bm{p}}}{2} (\hat{a}_{\bm{p}}\hat{a}^\dagger_{\bm{p}}+\hat{a}^\dagger_{\bm{p}}\hat{a}_{\bm{p}})\\ & = \int \frac{d^3 p}{(2\pi)^3} \omega_{\bm{p}} (\hat{a}_{\bm{p}}^\dagger \hat{a}_{\bm{p}} + \frac{1}{2}[\hat{a}_{\bm{p}}, \hat{a}^\dagger_{\bm{p}}]) \end{aligned}

上式第二项正比于 δ(0)\delta(0)，是一个无限大的常量，它是所有振动模式零点能的总和。由于实验中只能观测到能量的变化（相对于基态而言），因此我们实际上可以忽略这一项。那么哈密顿量为：

H^=∫d3p(2π)3ωpa^p†a^p(25)\hat{H} =\int \frac{d^3 p}{(2\pi)^3} \omega_{\bm{p}} \hat{a}_{\bm{p}}^\dagger \hat{a}_{\bm{p}} \tag{25}

另外，容易给出哈密顿量与阶梯算子的对易关系：

[H^,a^p†]=ωpa^p†[H^,a^p]=−ωpa^p(26)[\hat{H}, \hat{a}_{\bm{p}}^\dagger] = \omega_{\bm{p}}\hat{a}_{\bm{p}}^\dagger\quad [\hat{H}, \hat{a}_{\bm{p}}] = -\omega_{\bm{p}}\hat{a}_{\bm{p}} \tag{26}

由此，我们同样用 ∣0⟩|0\rangle 表示 基态（真空态）。满足：

a^p∣0⟩=0,∀ p(27)\hat{a}_{\bm{p}}|0\rangle =0,\quad \forall\ \bm{p} \tag{27}

那么真空态的能量为零。那么态 a^p†∣0⟩\hat{a}_{\bm{p}}^\dagger|0\rangle 的能量为：

H^a^p†∣0⟩=(a^p†H^+[H^,a^p†])∣0⟩=ωpa^p†∣0⟩\hat{H}\hat{a}_{\bm{p}}^\dagger|0\rangle = (\hat{a}_{\bm{p}}^\dagger\hat{H}+[\hat{H},\hat{a}_{\bm{p}}^\dagger])|0\rangle = \omega_{\bm{p}}\hat{a}_{\bm{p}}^\dagger|0\rangle

那么态 a^p†∣0⟩\hat{a}_{\bm{p}}^\dagger|0\rangle 的能量为 ωp\omega_{\bm{p}}。我们得到：将产生算子 a^p†\hat{a}^\dagger_{\bm{p}} 作用于真空态将得到其他能量本征值的态，例如：

a^p†a^q†∣0⟩\hat{a}_{\bm{p}}^\dagger \hat{a}_{\bm{q}}^\dagger|0\rangle

表示能量为 ωp+ωq\omega_{\bm{p}}+\omega_{\bm{q}} 的态。

在介绍能量-动量张量时，我们给出了场的物理动量：

P=−∫d3xπ(x)∇ϕ(x)(28)\bm{P}=-\int d^3x \pi(\bm{x})\nabla \phi(\bm{x}) \tag{28}

同样的方法，可以对动量对角化：

P^=−∫d3xπ^(x)∇ϕ^(x)=−∫d3x∫d3pd3q(2π)6(−iωp4ωq)ei(p+q)⋅xiq(a^p−a^−p†)(a^q+a^−q†)=−∫d3pd3q(2π)3δ(3)(p+q)(−iωp4ωq)iq(a^p−a^−p†)(a^q+a^−q†)=∫d3p(2π)312p(a^p−a^−p†)(a^−p+a^p†)=∫d3p(2π)312p(a^pa^−p−a^−p†a^−p+a^pa^p†−a^−p†a^p†)(29)\begin{aligned} \hat{\bm{P}}&=-\int d^3x \hat{\pi}(\bm{x})\nabla \hat{\phi}(\bm{x})\\ &=-\int d^3x \int \frac{d^3pd^3q}{(2\pi)^6} (-i\sqrt{\frac{\omega_{\bm{p}}}{4\omega_{\bm{q}}}})e^{i(\bm{p}+\bm{q})\cdot\bm{x}}i\bm{q}(\hat{a}_{\bm{p}}-\hat{a}^\dagger_{-\bm{p}})(\hat{a}_{\bm{q}}+\hat{a}^\dagger_{-\bm{q}})\\ &=-\int \frac{d^3pd^3q}{(2\pi)^3}\delta^{(3)}(\bm{p}+\bm{q}) (-i\sqrt{\frac{\omega_{\bm{p}}}{4\omega_{\bm{q}}}})i\bm{q}(\hat{a}_{\bm{p}}-\hat{a}^\dagger_{-\bm{p}})(\hat{a}_{\bm{q}}+\hat{a}^\dagger_{-\bm{q}})\\ &=\int \frac{d^3p}{(2\pi)^3}\frac{1}{2}\bm{p}(\hat{a}_{\bm{p}}-\hat{a}^\dagger_{-\bm{p}})(\hat{a}_{-\bm{p}}+\hat{a}^\dagger_{\bm{p}})\\ &=\int \frac{d^3p}{(2\pi)^3}\frac{1}{2}\bm{p}(\hat{a}_{\bm{p}}\hat{a}_{-\bm{p}}-\hat{a}^\dagger_{-\bm{p}}\hat{a}_{-\bm{p}}+\hat{a}_{\bm{p}}\hat{a}^\dagger_{\bm{p}}-\hat{a}^\dagger_{-\bm{p}}\hat{a}^\dagger_{\bm{p}})\\ \end{aligned}\tag{29}

考虑到：

∫d3p(2π)3pa^pa^−p=−∫d3p(2π)3pa^−pa^p=−∫d3p(2π)3pa^pa^−p\int \frac{d^3p}{(2\pi)^3}\bm{p}\hat{a}_{\bm{p}}\hat{a}_{-\bm{p}} = -\int \frac{d^3p}{(2\pi)^3}\bm{p}\hat{a}_{-\bm{p}}\hat{a}_{\bm{p}} = -\int \frac{d^3p}{(2\pi)^3}\bm{p}\hat{a}_{\bm{p}}\hat{a}_{-\bm{p}}

所以：

∫d3p(2π)3pa^pa^−p=0\int \frac{d^3p}{(2\pi)^3}\bm{p}\hat{a}_{\bm{p}}\hat{a}_{-\bm{p}} = 0

于是 (29)(29) 式称为：

P^=∫d3p(2π)312p(−a^−p†a^−p+a^pa^p†)=∫d3p(2π)312p(a^p†a^p+a^pa^p†)=∫d3p(2π)3p(a^p†a^p+12[a^p,a^p†])\begin{aligned} \hat{\bm{P}} &= \int \frac{d^3p}{(2\pi)^3}\frac{1}{2}\bm{p}(-\hat{a}^\dagger_{-\bm{p}}\hat{a}_{-\bm{p}}+\hat{a}_{\bm{p}}\hat{a}^\dagger_{\bm{p}})\\ &=\int \frac{d^3p}{(2\pi)^3}\frac{1}{2}\bm{p}(\hat{a}^\dagger_{\bm{p}}\hat{a}_{\bm{p}}+\hat{a}_{\bm{p}}\hat{a}^\dagger_{\bm{p}})\\ &= \int \frac{d^3p}{(2\pi)^3}\bm{p}(\hat{a}^\dagger_{\bm{p}}\hat{a}_{\bm{p}}+\frac{1}{2}[\hat{a}_{\bm{p}},\hat{a}^\dagger_{\bm{p}}])\\ \end{aligned}

其中第二项表示真空的动量，这一项是无法被观测的，去掉这一项后我们得到：

P^=∫d3p(2π)3pa^p†a^p\hat{\bm{P}} = \int \frac{d^3p}{(2\pi)^3} \bm{p}\hat{a}_{\bm{p}}^\dagger \hat{a}_{\bm{p}}

容易得到下列对易关系：

[P^,a^p†]=pa^p†[P^,a^p]=−pa^p(26)[\hat{\bm{P}}, \hat{a}_{\bm{p}}^\dagger] = \bm{p}\hat{a}_{\bm{p}}^\dagger\quad [\hat{\bm{P}}, \hat{a}_{\bm{p}}] = -\bm{p}\hat{a}_{\bm{p}} \tag{26}

同理，将产生算子 a^p†\hat{a}^\dagger_{\bm{p}} 作用于真空态 ∣0⟩|0\rangle，得到的态 a^p†∣0⟩\hat{a}^\dagger_{\bm{p}}|0\rangle 对应的动量为 p\bm{p}。

于是我们进行以下总结：将产生算子 a^p†\hat{a}^\dagger_{\bm{p}} 作用于真空态 ∣0⟩|0\rangle 会得到能量为 ωp\omega_{\bm{p}}、动量为 p\bm{p} 的态 a^p†∣0⟩\hat{a}_{\bm{p}}^\dagger|0\rangle。我们将其看作 a^p†\hat{a}_{\bm{p}}^\dagger 激发出了一个具有相应能量、动量的 粒子。将湮灭算子 a^p†\hat{a}^\dagger_{\bm{p}} 作用于真空态 ∣0⟩|0\rangle 进行作用会使能量下降 ωp\omega_{\bm{p}}、动量减少 p\bm{p}，我们可以看作 a^p\hat{a}_{\bm{p}} 湮灭了一个对应粒子。

考虑到 ap†,aq†a^\dagger_{\bm{p}},a^\dagger_{\bm{q}} 是对易的，由此 ap†aq†∣0⟩a_{\bm{p}}^\dagger a_{\bm{q}}^\dagger|0\rangle 与 aq†ap†∣0⟩a_{\bm{q}}^\dagger a_{\bm{p}}^\dagger|0\rangle 表示同一个两粒子态；并且一个模式 p\bm{p} 上可以占据任意多个粒子。由此可以得到 Klein-Gordon 场的粒子服从 玻色-爱因斯坦统计。对应描述的粒子为 玻色子 boson。

单粒子态

现在我们考虑表示一个粒子的 单粒子态。对于真空态，我们有 ⟨0∣0⟩=1\langle 0|0\rangle = 1。考虑一个含有动量为 p\bm{p} 的粒子的单粒子态 ∣p⟩|\bm{p}\rangle，有:

∣p⟩∝a^p†∣0⟩|\bm{p}\rangle \propto \hat{a}_{\bm{p}}^\dagger|0\rangle

如果定义 ∣p⟩=a^p†∣0⟩|\bm{p}\rangle = \hat{a}_{\bm{p}}^\dagger|0\rangle，我们得到：

⟨q∣p⟩=⟨0∣aqap†∣0⟩=⟨0∣[aq,ap†]∣0⟩=(2π)3δ(3)(p−q)\langle\bm{q}|\bm{p}\rangle = \langle 0|a_{\bm{q}} a_{\bm{p}}^\dagger |0\rangle = \langle 0|[a_{\bm{q}},a_{\bm{p}}^\dagger] |0\rangle = (2\pi)^3\delta^{(3)}(\bm{p}-\bm{q})

但是这是不合适的，因为上述条件并不是洛伦兹不变的。

洛伦兹不变：即在洛伦兹变换下不发生变化。我们之后将仔细讨论。

我们建议取：

∣p⟩=2Epap†∣0⟩(27)|\bm{p}\rangle = \sqrt{2E_{\bm{p}}} a^\dagger_{\bm{p}} |0\rangle \tag{27}

如此给出的归一化条件将是洛伦兹不变的：

⟨q∣p⟩=(2π)32Epδ(3)(p−q)\langle\bm{q}|\bm{p}\rangle = (2\pi)^3 2E_{\bm{p}}\delta^{(3)}(\bm{p}-\bm{q})

证明：我们可以考虑一个特定的洛伦兹变换，首先 rotation 是显然保证上式的不变性的。下面考虑 boost，例如对 p3p_3 的 boost：

p3′=γ(p3+βE)E′=γ(E+βp3)\begin{aligned} &p_3' = \gamma(p_3+\beta E)\\ &E' = \gamma(E+\beta p_3)\\ \end{aligned}

可得：

E′δ(3)(p′−q′)=E′δ(p1−q1)δ(p2−q2)δ(p3′−q3′)=E′δ(p1−q1)δ(p2−q2)δ(p3′−q3′)=E′δ(p1−q1)δ(p2−q2)δ(p3−q3)(dp3′dp3)−1=E′δ(3)(p−q)(γ(1+βdEdp3))−1=E′δ(3)(p−q)(γ(1+βp3E))−1=Eδ(3)(p−q)\begin{aligned} E' \delta^{(3)}(\bm{p}'-\bm{q}') &= E' \delta(p_1-q_1)\delta(p_2-q_2)\delta(p'_3-q'_3)\\ &= E' \delta(p_1-q_1)\delta(p_2-q_2)\delta(p'_3-q'_3)\\ &= E' \delta(p_1-q_1)\delta(p_2-q_2)\delta(p_3-q_3) (\frac{dp_3'}{dp_3})^{-1}\\ &= E' \delta^{(3)}(\bm{p}-\bm{q}) (\gamma(1+\beta \frac{dE}{dp_3}))^{-1}\\ &= E' \delta^{(3)}(\bm{p}-\bm{q}) (\gamma(1+\beta \frac{p_3}{E}))^{-1}\\ &= E \delta^{(3)}(\bm{p}-\bm{q})\\ \end{aligned}

上述推导中利用以下公式：

δ(f(x)−f(x0))=1∣f′(x0)∣δ(x−x0)E2=p2+m2⇒2EdE=2pdp\begin{aligned} &\delta(f(x)-f(x_0)) = \frac{1}{|f'(x_0)|}\delta(x-x_0)\\ &E^2 = p^2 + m^2 \Rightarrow 2EdE = 2pdp\\ \end{aligned}

考虑对波函数的洛伦兹变换 Λ\Lambda，这等价于用一个幺正算子作用于波函数。首先真空是洛伦兹不变的：

U(Λ)∣0⟩=∣0⟩U(\Lambda)|0\rangle = |0\rangle

对于单粒子态有：

U(Λ)∣p⟩=∣Λp⟩U(\Lambda)|\bm{p}\rangle = |\Lambda\bm{p}\rangle

由此可得：

U(Λ)∣p⟩=U(Λ)2Epap†∣0⟩=2EpU(Λ)ap†U−1(Λ)∣0⟩∣Λp⟩=2EΛpaΛp†∣0⟩\begin{aligned} &U(\Lambda)|\bm{p}\rangle = U(\Lambda)\sqrt{2E_{\bm{p}}} a_{\bm{p}}^\dagger|0\rangle = \sqrt{2E_{\bm{p}}} U(\Lambda)a_{\bm{p}}^\dagger U^{-1}(\Lambda) |0\rangle\\ &|\Lambda\bm{p}\rangle =\sqrt{2E_{\Lambda\bm{p}}} a_{\Lambda\bm{p}}^\dagger|0\rangle\\ \end{aligned}

得到产生算子在洛伦兹变化下的形式：

U(Λ)ap†U−1(Λ)=EΛpEpaΛp†(28)U(\Lambda)a_{\bm{p}}^\dagger U^{-1}(\Lambda) = \sqrt{\frac{E_{\Lambda\bm{p}}}{E_{\bm{p}}}} a_{\Lambda\bm{p}}^\dagger \tag{28}

所有单粒子态构成一组正交完备基，这就是 完备性关系：

(1)one−particle=∫d3p(2π)3∣p⟩12Ep⟨p∣(29)(1)_{one-particle} = \int \frac{d^3p}{(2\pi)^3} |\bm{p}\rangle\frac{1}{2E_{\bm{p}}} \langle \bm{p}| \tag{29}

可以得到完备性关系是洛伦兹不变的。具体来说，只要注意到以下积分是洛伦兹不变的：

∫d3p(2π)312Ep=∫d4p(2π)32πδ(p2−m2)∣p0>0\int \frac{d^3p}{(2\pi)^3} \frac{1}{2E_{\bm{p}}} = \int \frac{d^4p}{(2\pi)^3} 2\pi\delta(p^2-m^2)|_{p^0>0}

另外我们使用 ϕ(x)\phi(\bm{x}) 作用于 ∣0⟩|0\rangle 也会得到一个单粒子态：

ϕ(x)∣0⟩=∫d3p(2π)312ωp(apeip⋅x+ap†e−ip⋅x)∣0⟩=∫d3p(2π)312ωpap†e−ip⋅x∣0⟩=∫d3p(2π)312Epe−ip⋅x∣p⟩\begin{aligned} \phi(\bm{x})|0\rangle &=\int \frac{d^3p}{(2\pi)^3} \frac{1}{\sqrt{2\omega_{\bm{p}}}}(a_{\bm{p}}e^{i\bm{p}\cdot\bm{x}}+a_{\bm{p}}^\dagger e^{-i\bm{p}\cdot\bm{x}})|0\rangle\\ &=\int \frac{d^3p}{(2\pi)^3} \frac{1}{\sqrt{2\omega_{\bm{p}}}}a_{\bm{p}}^\dagger e^{-i\bm{p}\cdot\bm{x}}|0\rangle\\ &=\int \frac{d^3p}{(2\pi)^3} \frac{1}{2E_{\bm{p}}}e^{-i\bm{p}\cdot\bm{x}}|\bm{p}\rangle\\ \end{aligned}

这是一些具有确定动量的单粒子态的叠加。我们解释为：ϕ(x)\phi(\bm{x}) 作用于 ∣0⟩|0\rangle 在的效果相当于在位置 x\bm{x} 产生了一个粒子。

我们作如下验证：

⟨0∣ϕ(x)∣p⟩=∫d3p(2π)312Eqeiq⋅x⟨q∣p⟩=eip⋅x\langle 0|\phi(\bm{x})|\bm{p}\rangle = \int \frac{d^3p}{(2\pi)^3}\frac{1}{2E_{\bm{q}}}e^{i\bm{q}\cdot\bm{x}} \langle \bm{q}|\bm{p}\rangle =e^{i\bm{p}\cdot\bm{x}}

我们发现其结果正为平面波，即可以认为：

ϕ(x)∣0⟩∼∣x⟩\phi(\bm{x})|0\rangle \sim |\bm{x}\rangle