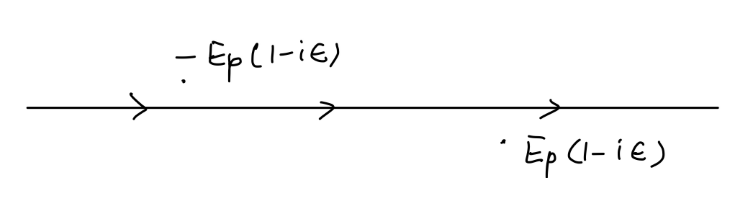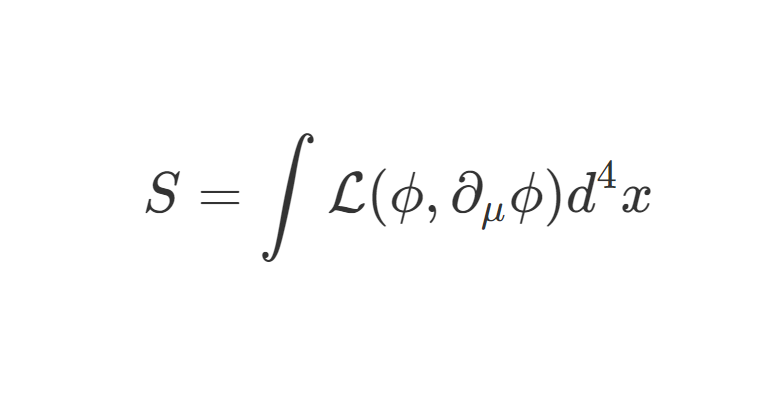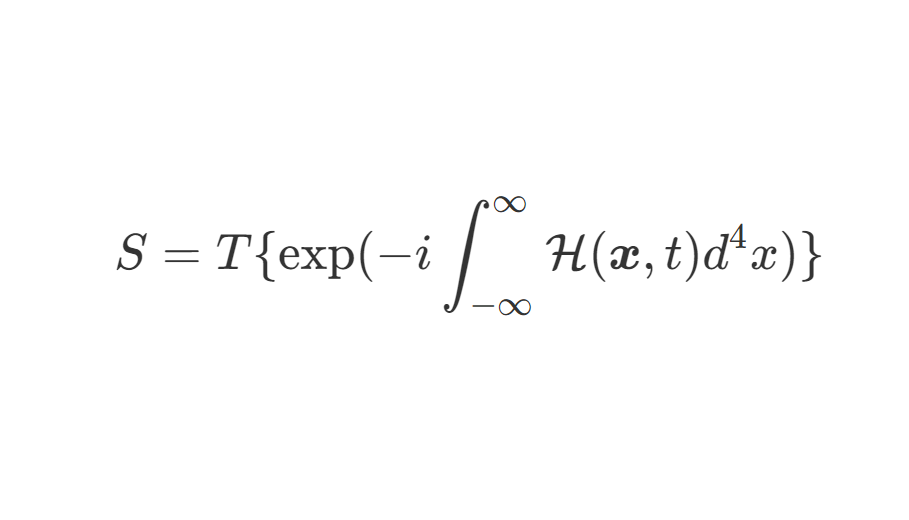海森堡绘景
我们之前一直在 薛定谔绘景 Schrödinger picture 中讨论问题,在薛定谔绘景中:
-
态矢 ∣ψ⟩ 随时间演化。
-
算子 A^ 不 随时间演化。
态矢随时间的演化满足薛定谔方程:
i∂t∂∣ψ(t)⟩=H∣ψ(t)⟩(1)
上式若在特定的表象下写出(例如坐标表象):
i∂t∂ψ(x,t)=Hψ(x,t)
这是我们所熟悉的形式。
方程 (1) 的形式解为:
∣ψ(t)⟩=exp(−iHt)∣ψ(0)⟩(2)
若哈密顿量含时(例如含有依赖时间的势能项),那么 (1) 的形式解为:
∣ψ(t)⟩=exp(−i∫0tH(t′)dt′)∣ψ(0)⟩
若哈密顿量在不同时刻的值并不对易,还要引入 时序符号 time-ordered symbol:
∣ψ(t)⟩=T{exp(−i∫0tH(t′)dt′)}∣ψ(0)⟩
我们不做过多讨论,以下默认哈密顿量不含时,我们直接应用 (2)。
我们引入一个算子 U,其定义为:
U(t,0)≡exp(−iHt)
一般来说:
U(t1,t2)≡exp(−iH(t1−t2))
不难得到 U 具有以下性质:
-
U(t1,t2)U†(t1,t2)=1 幺正性
-
U†(t1,t2)=U(t2,t1)
-
U(t1,t2)U(t2,t3)=U(t1,t3)
-
[H,U]=0
那么在薛定谔绘景下,态矢的演化可以用 U 表示为:
∣ψ(t)⟩S=U(t,0)∣ψ(0)⟩S(3)
取共轭,得到左矢量的演化规则:
S⟨ψ(t)∣=S⟨ψ(0)∣U†(t,0)(4)
这里我们使用下标 S 表示薛定谔绘景,以下相应会用下标 H 表示海森堡绘景。
现在我们在 海森堡绘景 Heisenberg picture 中进行讨论。在海森堡绘景中:
-
态矢 ∣ψ⟩ 不 随时间演化。
-
算子 A^ 随时间演化。
我们假设在 t=0 时,所有绘景中算子和态矢的取值相同。而根据海森堡绘景中的定义,其态矢为:
∣ψ(t)⟩H≡∣ψ(0)⟩H=∣ψ(0)⟩S(4)
物理量的观测值是 绘景无关 的。这意味着:
⟨A^⟩=H⟨ψ∣A^H(t)∣ψ⟩H=S⟨ψ(t)∣A^S∣ψ(t)⟩S(5)
其中:
H⟨ψ∣A^H(t)∣ψ⟩H=S⟨ψ(0)∣A^H(t)∣ψ(0)⟩S=S⟨ψ(t)∣U(t,0)A^H(t)U†(t,0)∣ψ(t)⟩S=S⟨ψ(t)∣A^S∣ψ(t)⟩S
得到:
A^H(t)=U†(t,0)A^SU(t,0)(6)
海森堡绘景中,算子满足的运动方程为:
∂t∂A^H(t)=(∂t∂U†(t,0))A^SU(t,0)+U†(t,0)A^S(∂t∂U(t,0))=iHU†(t,0)A^SU(t,0)−U†(t,0)A^SU(t,0)iH=iHA^H(t)−iA^H(t)H=i[H,A^H(t)](7)
这就是 海森堡方程 Heisenberg equation ,即海森堡绘景下的运动方程。
海森堡绘景下的 Klein-Gordon 场
现在,我们需要在海森堡绘景下讨论 Klein-Gordon 场。
首先,场量、动量应当依赖于时间,根据 (6) 式,有:
ϕ^(x)π^(x)=ϕ^(x,t)=eiHtϕ^(x)e−iHt=π^(x,t)=eiHtπ^(x)e−iHt
我们这里的表示:x 指四维坐标,x 指空间坐标。注意这里已经进行过一次量子化了,所以才可以谈论相应的绘景:ϕ^(x) 对应于海森堡绘景,ϕ^(x) 对应于薛定谔绘景。
在海森堡绘景中,有 等时对易关系:
[ϕ^(x,t),π^(x′,t)]=e−iHt[ϕ^(x),π^(x′)]eiHt=iδ(x−x′)(8)
对应的运动方程为:
∂t∂ϕ^(x,t)=i[H,ϕ^(x,t)]=i[∫d3x′(21π^2(x′,t)+21(∇′ϕ^(x′,t))2+21m2ϕ^2(x′,t),ϕ^(x,t)]=i[∫d3x′21π^2(x′,t),ϕ^(x,t)]=2i∫d3x′[π^2(x′,t),ϕ^(x,t)]=∫d3x′π^(x′,t)δ(3)(x−x′)=π^(x,t)(9)
∇′ 表示对 x′ 求偏导。
以及:
∂t∂π^(x,t)=i[H,π^(x,t)]=i[∫d3x′(21π^2(x′,t)+21(∇′ϕ^(x′,t))2+21m2ϕ^2(x′,t),π^(x,t)]=i[∫d3x′(21(∇′ϕ^(x′,t))2+21m2ϕ^2(x′,t),π^(x,t)](10)
考虑到:
∫d3x21[(∇′ϕ^(x′,t))2,π^(x,t)]=∫d3x′∇′ϕ^(x′,t)[∇′ϕ^(x′,t),π^(x,t)]=∫d3x′∇′ϕ^(x′,t)∇′[ϕ^(x′,t),π^(x,t)]=−∫d3x′∇′ϕ^(x′,t)∇′δ(x′−x)=−∫d3x′∇′(∇′ϕ^(x′,t)δ(x′−x))−δ(x′−x)∇′2ϕ^(x′,t)=−∫ΣdS⋅∇′ϕ^(x′,t)δ(x′−x)+∫d3x′δ(x′−x)∇′2ϕ^(x′,t)=∇2ϕ^(x,t)
倒数第二行中第一项为零,因为可以选取 Σ 使,x∈/Σ。
代入 (10) 式中,得到:
∂t∂π^(x,t)=(∇2−m2)ϕ^(x,t)(11)
方程 (9)(11) 实际上就会给出 Klein-Gordon 方程:
∂t2∂2ϕ^(x,t)=(∇2−m2)ϕ^(x,t)(12)
在量子化的过程中,我们引入了阶梯算子,在海森堡绘景下它们也应当是随时间演化的:
考虑到:
[H,a^p]=−Epa^p⇒Ha^p=a^p(H−Ep)
由此:
eiHta^p=n=0∑∞n!(it)nHna^p=a^pn=0∑∞n!(it)n(H−Ep)n=a^pei(H−Ep)t
于是得到以下关系,给出了海森堡绘景中的阶梯算子表达式:
{eiHta^pe−iHt=a^pe−iEpteiHta^p†e−iHt=a^p†eiEpt(13)
Klein-Gordon 场可以用阶梯算子表示为:
ϕ^(x,t)=eiHtϕ^(x)e−iHt=eiHt[∫(2π)3d3p2Ep1(a^peip⋅x+a^p†e−ip⋅x)]e−iHt=∫(2π)3d3p2Ep1(eiHta^pe−iHteip⋅x+eiHta^p†e−iHte−ip⋅x)=∫(2π)3d3p2Ep1(a^pe−i(Ept−p⋅x)+a^p†ei(Ept−p⋅x))=∫(2π)3d3p2Ep1(a^pe−ip⋅x+a^p†eip⋅x)(14)
利用运动方程 (9),可以得到:
π^(x,t)=∂t∂ϕ^(x,t)=∫(2π)3d3p(−i)2Ep(a^pe−ip⋅x+a^p†eip⋅x)
注意到对易关系:
[P^,a^p]=−pa^p(15)
注意 P^ 为动量算子,p 为动量算子的一个本征值。
可以得到:
⎩⎨⎧e−iP^⋅xa^peiP^⋅x=a^peip⋅xe−iP^⋅xa^p†eiP^⋅x=a^p†e−ip⋅x(16)
此时,注意到 (14) 式的形式,可以写为:
ϕ^(x,t)=∫(2π)3d3p2Ep1(a^pe−ip⋅x+a^p†eip⋅x)=ei(Ht−P^⋅x)ϕ^(0)e−i(Ht−P^⋅x)=eiP⋅xϕ^(0)e−iP⋅x(17)
传播子与因果性
在薛定谔绘景中,态矢 ∣y⟩ 在演化 t 时间后与态矢 ∣x⟩ 的重叠程度为:
⟨x∣e−iHt∣y⟩
这可以解释为一个粒子从 y 传播到 x 的概率幅,这总是一个非零值。在场论中,我们也可以构造一个类似的 传播子 propagator(假设 x0>y0):
⟨x∣e−iHt∣y⟩∼⟨0∣ϕ^(x)e−iHtϕ^(y)∣0⟩=⟨0∣eiHx0ϕ^(x)e−iHx0eiHy0ϕ^(y)e−iHy0∣0⟩=⟨0∣ϕ^(x)ϕ^(y)∣0⟩≡D(x−y)
对于 Klein-Gordon 场的情形,有
D(x−y)=⟨0∣ϕ^(x)ϕ^(y)∣0⟩=∫(2π)6d3pd3q4EpEq1e−i(p⋅x−q⋅y)⟨0∣a^pa^q†∣0⟩=∫(2π)6d3pd3q4EpEq1e−i(p⋅x−q⋅y)⟨0∣[a^p,a^q†]∣0⟩=∫(2π)3d3p2Ep1e−ip⋅(x−y)(18)
可以看出,D(x−y) 是一个洛伦兹不变的量。进一步的,我们想讨论如下物理量:
⟨0∣[ϕ^(x),ϕ^(y)]∣0⟩=∫(2π)3d3p2Ep1(e−ip⋅(x−y)−eip⋅(x−y))=D(x−y)−D(y−x)(19)
我们对这个 (19) 式的结果做一些分析。
- 当间隔 x−y 是 类空 space like((x−y)2<0)时,我们总可以找到如下连续的洛伦兹变换:
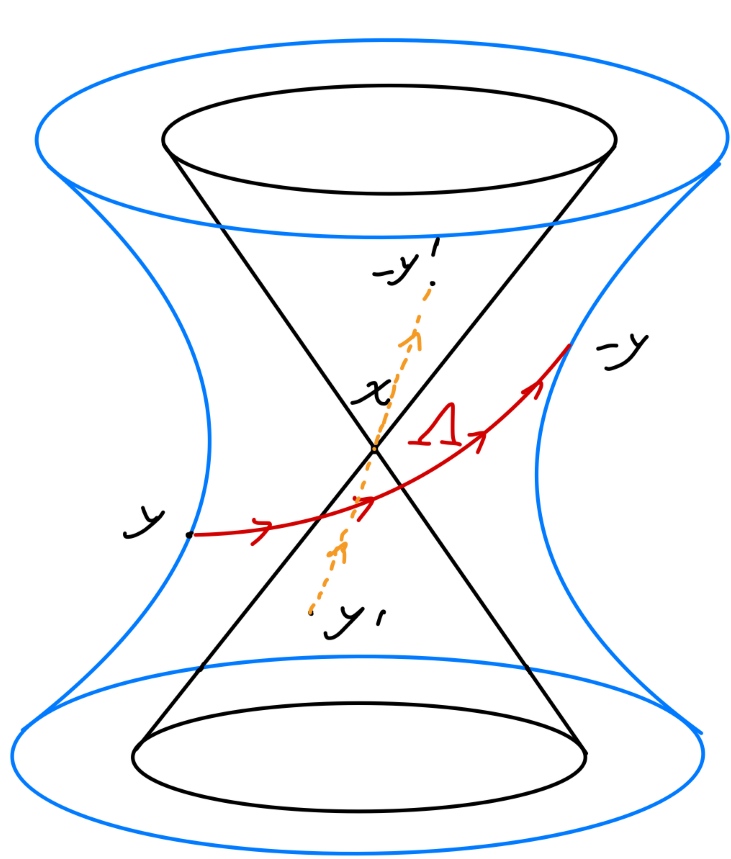
x−y→Λy−x
立刻得到:
D(x−y)=D(y−x)⇒⟨0∣[ϕ^(x),ϕ^(y)]∣0⟩=0,∀ (x−y)2<0(20)
- 当间隔是 类时 time like((x−y)2>0)时,并不存在这样的一个连续洛伦兹变换。一般来说:
D(x−y)=D(y−x)⇒⟨0∣[ϕ^(x),ϕ^(y)]∣0⟩=0
我们不妨停下来思考一下两个物理量对易意味着什么。在薛定谔绘景中,若两个物理量对易,那么它们是可以被同时测量的,彼此不可能相互影响。推广到海森堡绘景中,若两个物理量对易,那么我们断言:这两个物理量并不会存在因果关系。狭义相对论告诉我们,两个具有类时间隔的事件不可能有 因果关系 causality。
对于两个可观测量 H(x),H(x′),因果性要求:
[H(x),H(x′)]=0,∀ (x−x′)2<0(21)
可观测量一般由偶数个场量构成,可以证明只要场量满足 (20),那么因果性,即 (21) 将满足。下面举例说明:
对于 H(x)=21m2ϕ2(x),有:
∀ (x−x′)2<0[H(x),H(x′)]===41m4[ϕ2(x),ϕ2(x′)]41m4(ϕ(x)ϕ(x′)[ϕ(x),ϕ(x′)]+ϕ(x)[ϕ(x),ϕ(x′)]ϕ(x′)+ϕ(x′)[ϕ(x),ϕ(x′)]ϕ(x)+[ϕ(x),ϕ(x′)]ϕ(x)ϕ(x′))0
在非相对论量子力学中,即使对于类空间隔,粒子传播的概率幅总是非零的。而以上我们对因果性的解释也反映了我们从 “场” 的观点出发的必要性。
我们再来看 ⟨0∣[ϕ^(x),ϕ^(y)]∣0⟩,x0>y0 的物理解释。其中 ⟨0∣ϕ^(x)ϕ^(y)∣0⟩ 为粒子从 y 传播到 x 的概率幅。那么:
⟨0∣eiHy0ϕ^(y)e−iHy0eiHx0ϕ^(x)e−iHx0∣0⟩=⟨0∣ϕ(y)eiHtϕ(x)∣0⟩∼⟨y∣eiHt∣x⟩
注意到演化算子形式的差异:它是逆着时间方向进行演化的。我们解释为这是一个从 x 传播到 y 的 反粒子 的概率幅。为了保证因果性,我们必须引入反粒子,对于 Klein-Gordon 场,其反粒子就是本身。
有关反粒子、因果性,我们以后会专门讨论。
Klein-Gordon 传播子
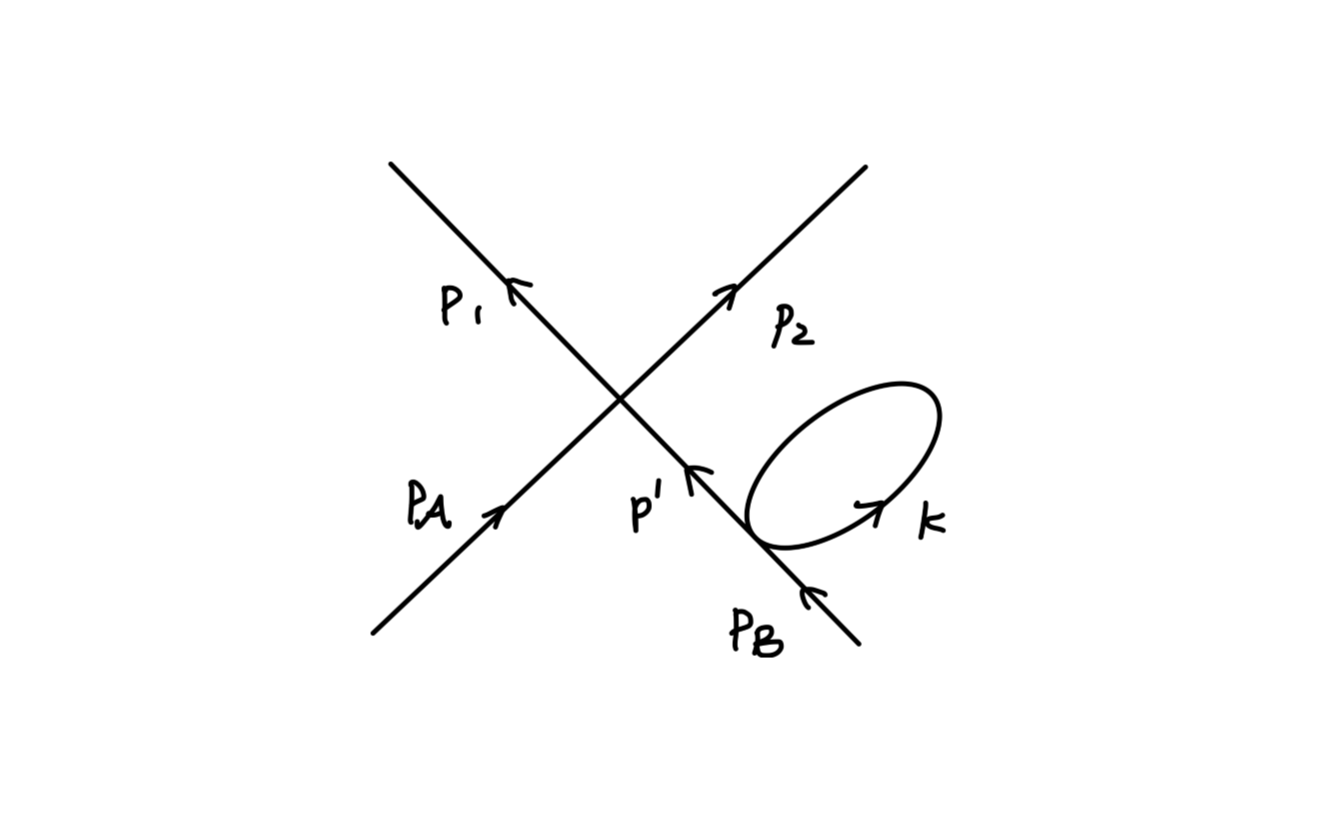
利用 留数定理 可以将 (19) 写为:
⟨0∣[ϕ^(x),ϕ^(y)]∣0⟩=∫(2π)3d3p2Ep1(e−ip⋅(x−y)−eip⋅(x−y))=∫(2π)3d3p(2Ep1e−ip⋅(x−y)∣p0=Ep−2Ep1e−ip⋅(x−y)∣p0=−Ep)x0>y0=∫(2π)3d3p∮2πidp0p2−m2−1e−ip⋅(x−y)=∫(2π)4d4pp2−m2ie−ip⋅(x−y)(22)
倒数第二行应用了留数定理,对应的极点为 p0=±Ep,选取的围线如下图所示。
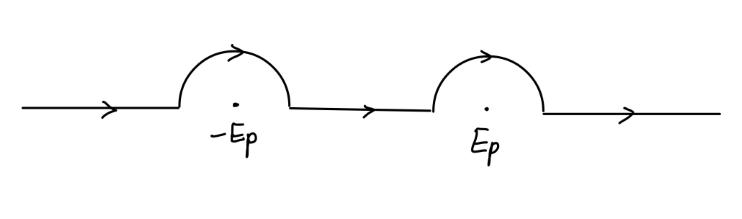
对于该路径在 y0>x0 的取值,我们可以选取围线向上闭合,此时围线中并不包含任何极点,容易得到:
∫(2π)4d4pp2−m2ie−ip⋅(x−y)x0<y0=0
我们定义 Klein-Gordon 传播子 为:
DR≡θ(x0−y0)⟨0∣[ϕ^(x),ϕ^(y)]∣0⟩(23)
其中
θ(x0−y0)={10x0>y0x0<y0
为 Heviside 函数(单位阶跃函数)。
(23) 式的定义就与选取特定路径后的 (22) 式等价。
我们用 Klein-Gordon 算子作用于 Klein-Gordon 传播子:
====(∂2+m2)DR(x−y)(∂2+m2)(θ(x0−y0)⟨0∣[ϕ^(x),ϕ^(y)]∣0⟩)(∂2θ(x0−y0))⟨0∣[ϕ^(x),ϕ^(y)]∣0⟩+2∂μθ(x0−y0)⟨0∣∂μ[ϕ^(x),ϕ^(y)]∣0⟩+(θ(x0−y0)(∂2+m2)⟨0∣[ϕ^(x),ϕ^(y)]∣0⟩)−δ(x0−y0)⟨0∣[π^(x),ϕ^(x)]+2δ(x0−y0)⟨0∣[π^(x),ϕ^(x)]−iδ(4)(x−y)
即:
(∂2+m2)DR(x−y)=−iδ(4)(x−y)(24)
考虑在 x0<y0 时,Klein-Gordon 传播子为零。所以 Klein-Gordon 传播子其实就是 Klein-Gordon 场的 推迟格林函数 retarded Green’s function。
在动量空间中有:
DR(x−y)=∫(2π)4d4pe−ip⋅(x−y)D~R(p)(25)
将 (25) 代入 (24) 式中得到:
D~R(p)=p2−m2i(26)
代入 (27) 得到:
DR(x−y)=∫2πid4pe−ip⋅(x−y)p2−m2i(27)
注意,通过以上的推导可知,这里的积分路径实际上有四种不同的选取方法。当我们考虑如下选取积分路径时:
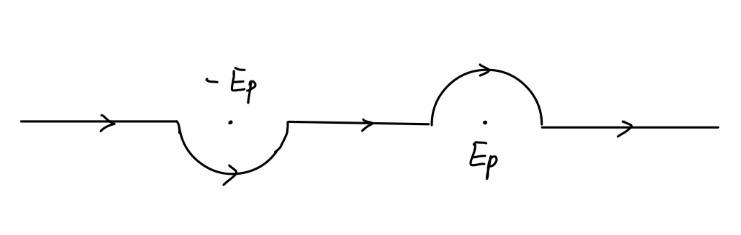
我们可以在传播子的分母添加一很小的虚部,极点成为 p0=±(Ep−iϵ)。那么上述积分可以等价于沿着实轴的积分:
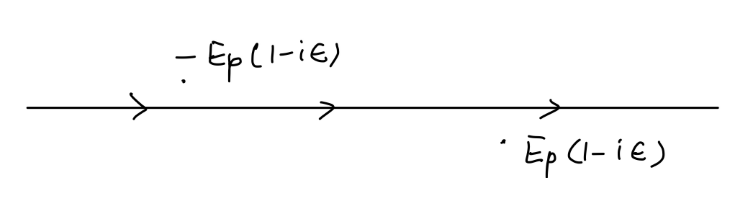
DF(x−y)≡∫(2π)4d4pp2−m2+iϵie−ip⋅(x−y)(28)
这称为 Klein-Gordon 粒子的 费曼传播子 Feynman propagator。在 x0>y0 与 x0<y0 的情况,可以选择不同的闭合围线进行计算:
DF(x−y)={D(x−y)x0>y0D(y−x)x0<y0=θ(x0−y0)⟨0∣ϕ(x)^ϕ(y)^∣0⟩+θ(y0−x0)⟨0∣ϕ(y)^ϕ(x)^∣0⟩≡⟨0∣Tϕ(x)ϕ(y)∣0⟩(29)
上述式子中引入了 时序符号 time-ordering symbol T:表示将时序符号后面的式子按照时间从晚到早排列。容易得到费曼传播子就是 Klein-Gordon 场的 格林函数 Green’s function。在动量空间中的费曼传播子为:
D~F(p)=p2−m2+iϵi(30)
这件事情在后面介绍的费曼规则中很重要。
有源 Klein-Gordon 场
现在考虑一个具有经典源的 Klein-Gordon 场:
(∂2+m2)ϕ(x)=j(x)(31)
对应的拉氏量为:
L=21∂μϕ∂μϕ−21m2ϕ2+j(x)ϕ(x)(32)
(31) 式的解将有两项构成:
ϕ(x)=ϕ0(x)+i∫d4yDR(x−y)j(y)=ϕ0(x)+i∫d4y∫(2π)3d3p2Ep1θ(x0−y0)(e−ip⋅(x−y)−eip⋅(x−y))j(y)
其中 ϕ0(x) 为自由 Klein-Gordon 场的解。我们现在考虑源仅在有限时间内开启。当源关闭后,总有 y0<x0。于是有:
ϕ(x)=ϕ0(x)+i∫d4y∫(2π)3d3p2Ep1(e−ip⋅(x−y)−eip⋅(x−y))j(y)=∫(2π)3d3p2Ep1(a^p+2Epij~(p))e−ip⋅x+h.c(33)
其中
j~(p)=∫d4yeip⋅yj(y)(34)
我们注意到 (33) 与 ϕ(x) 相比只是做了如下替换:
a^p→a^p+2Epij~(p)a^p†→a^p†−2Epij~∗(p)(35)
那么可以得到哈密顿量的形式如下:
H=∫(2π)3d3pEp(a^p†−2Epij~∗(p))(a^p+2Epij~(p))(36)
由于源的影响,系统的基态能量发生变化:
⟨0∣H∣0⟩=∫(2π)3d3p21∣j~(p)∣2(37)
源产生的粒子数目为:
N=∫(2π)3d3p2Ep1∣j~(p)∣2(38)