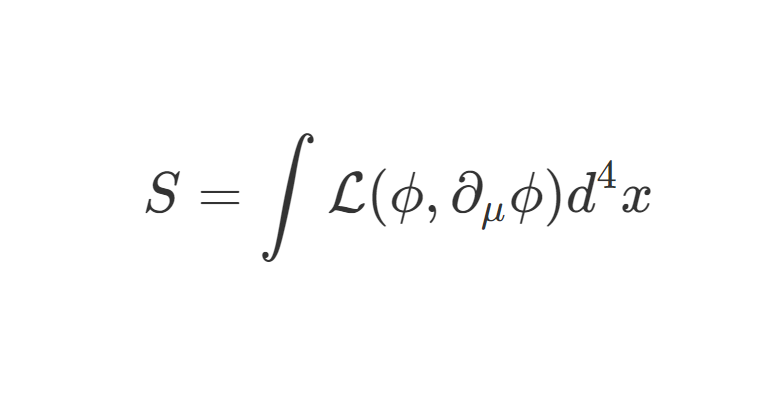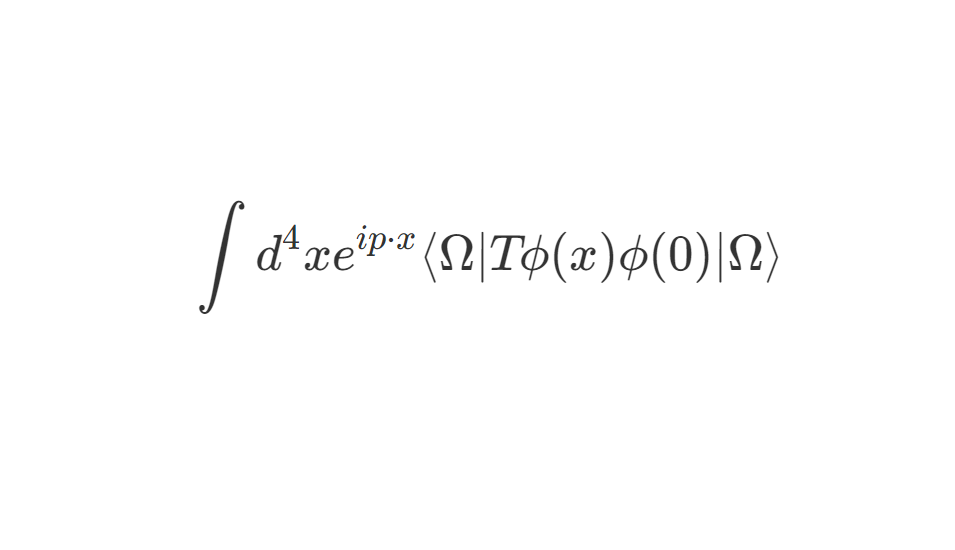量子场论笔记（十）：微扰论

微扰论

上一篇中我们介绍了散射矩阵的概念。但如何计算散射矩阵呢？对于自由场的情形，我们可以很好求解，但相互作用的加入使得问题变得复杂起来。此时哈密顿量可以写为：

$H = H_0 + V$

其中 $H_0$ 为自由场哈密顿量，$V$ 为相互作用项。

现在我们考虑：当相互作用很弱时，可以使用微扰论的方法处理。其主要思想是：得到自由场的解后，将相互作用作为微扰，求近似解。

典型的相互作用的拉格朗日量如下：

• $\phi^4$ 理论

$\begin{aligned} &\mathcal{L} = \frac{1}{2}(\partial_{\mu}\phi)^2 - \frac{1}{2}m^2\phi^2 - \frac{\lambda}{4}\phi^4 \\ &V = \frac{\lambda}{4}\phi^4\\ \end{aligned}\tag{1}$

• 量子电动力学 QED

$\begin{aligned} \mathcal{L}_{QED} &= \bar{\psi}(i\gamma^{\mu}D_{\mu}-m)\psi - \frac{1}{4}(F_{\mu\nu})^2\\ D_{\mu} &\equiv \partial_{\mu} + ieA_{\mu}(x)\\ V &= e\bar{\psi}\gamma^{\mu}\psi A_{\mu}\\ \end{aligned}\tag{2}$

• Yukawa 理论

$\begin{aligned} &\mathcal{L}_{Yukawa} = \mathcal{L}_{Dirac} + \mathcal{L}_{Klein-Gordon} - g\bar{\psi}\psi\phi\\ &V=g\bar{\psi}\psi\phi\\ \end{aligned}\tag{3}$

散射矩阵的微扰展开

对于散射矩阵，我们上一篇 量子场论笔记（九）：散射矩阵 中已经给出：

$\begin{aligned} &S_{\beta\alpha} = \delta(\beta-\alpha) -2i\pi \delta(E_{\beta}-E_{\alpha})T_{\beta\alpha}^+\\ &T_{\beta\alpha}^+ = \langle \Phi_{\beta}|V|\Psi_{\alpha}^+\rangle \end{aligned}\tag{4}$

入射态 $\Psi^+_{\alpha}$ 可以用 Lippmann-Schwinger 方程表示：

$\Psi^+_{\alpha} = \Phi_{\alpha} + \int d\gamma \frac{T_{\gamma\alpha}^+\Phi_{\gamma}}{E_{\alpha}-E_{\gamma}+i\epsilon}\tag{5}$

利用 $(5)$ 式，两边同时使用 $\langle \Phi_{\beta}|V$ 作用，得到：

$T_{\beta\alpha}^+ = V_{\beta\alpha} + \int d\gamma\frac{V_{\beta\gamma}T_{\gamma\alpha}^+}{E_{\alpha}-E_{\gamma}+i\epsilon} \tag{6}$

其中：

$V_{\beta\alpha} = \langle \Phi_{\beta}|V|\Phi_{\alpha}\rangle \tag{7}$

当相互作用很弱时，$\Psi_{\alpha}^{+}\rightarrow \Phi_{\alpha}$，此时 $T_{\beta\alpha} \rightarrow V_{\beta\alpha}$，$(6)$ 式中第一项正对应零阶项，而第二项对应于高阶项。那么反复利用 $(6)$ 式，我们自然地可以将 $T_{\beta\alpha}^+$ 进行微扰展开：

$\begin{aligned} T_{\beta\alpha}^+ =& V_{\beta\alpha} + \int d\gamma \frac{V_{\beta\gamma}V_{\gamma\alpha}}{E_{\alpha}-E_{\gamma}+i\epsilon}\\ &+ \int d\gamma d\gamma' \frac{V_{\beta\gamma}V_{\gamma\gamma'}V_{\gamma'\alpha}}{(E_{\alpha}-E_{\gamma}+i\epsilon)(E_{\alpha}-E_{\gamma'}+i\epsilon)}+\cdots\\ \end{aligned}\tag{8}$

由此，可以求得散射矩阵地微扰展开表达式。这被称为 old-fashioned perturbation theory。其缺点是：散射矩阵的洛伦兹不变性不能直观的得到。现在我们一般采用一个更简单的方法，称为 含时微扰论 time dependent perturbation theory。在上一篇中，我们得到散射矩阵实际上可以表示为：

$S = U(+\infty,-\infty)\tag{9}$

其中：

$U(\tau,\tau_0) = \exp(iH_0\tau) \exp(-iH(\tau-\tau_0))\exp(-iH_0\tau_0)\tag{10}$

由 $(10)$ 推导得到以下表达式：

$\begin{aligned} i\frac{\partial U(\tau,\tau_0)}{\partial \tau} &= \exp(iH_0\tau) (H-H_0) \exp(-iH(\tau-\tau_0))\exp(-iH_0\tau_0)\\ &= \exp(iH_0\tau)V\exp(-iH_0\tau) \exp(iH_0\tau) \exp(-iH(\tau-\tau_0))\exp(-iH_0\tau_0)\\ &= V(\tau)U(\tau,\tau_0) \end{aligned}\tag{11}$

其中：

$V(\tau) \equiv \exp(iH_0\tau)V\exp(-iH_0\tau) \tag{12}$

方程 $(11)$ 的解为：

$U(\tau,\tau_0) = 1 - i\int_{\tau_0}^{\tau} dt V(t)U(t,\tau_0) \tag{13}$

通过迭代，可以将 $U(\tau,\tau_0)$ 写为：

$\begin{aligned} U(\tau,\tau_0) &= 1 - i\int_{\tau_0}^{\tau}dt_1 V(t_1) + (-i)^2\int_{\tau_0}^{\tau}dt_1\int_{\tau_0}^{t_1}dt_2 V(t_1)V(t_2)\\ &\quad + (-i)^3\int_{\tau_0}^{\tau}dt_1\int_{\tau_0}^{t_1}dt_2 \int_{\tau_0}^{t_2}dt_3 V(t_1)V(t_2)V(t_3) + \cdots\\ \end{aligned}\tag{14}$

令 $\tau = \infty,\tau_0 = -\infty$，得到散射矩阵的微扰展开表达式：

$\begin{aligned} S &= U(+\infty,-\infty)\\ &= 1 - i\int_{-\infty}^{\infty}dt_1 V(t_1) + (-i)^2\int_{-\infty}^{\infty}dt_1\int_{-\infty}^{t_1}dt_2 V(t_1)V(t_2)\\ &\quad + (-i)^3\int_{-\infty}^{\infty}dt_1\int_{-\infty}^{t_1}dt_2 \int_{-\infty}^{t_2}dt_3 V(t_1)V(t_2)V(t_3) + \cdots\\ \end{aligned}\tag{15}$

这里利用时序符号，可以将式 $(15)$ 简化。例如：

$\begin{aligned} &\int_{\tau_0}^{\tau}dt_1\int_{\tau_0}^{t_1}dt_2 V(t_1)V(t_2)\\ =&\int_{-\infty}^{\infty}dt_1\int_{-\infty}^{\infty} dt_2 \theta(t_1-t_2) V(t_1)V(t_2)\\ =& \int_{-\infty}^{\infty}dt_1 dt_2 \theta(t_1-t_2) V(t_1)V(t_2)\\ =& \frac{1}{2} (\int_{-\infty}^{\infty}dt_1 dt_2 \theta(t_1-t_2) V(t_1)V(t_2) + \int_{-\infty}^{\infty}dt_2 dt_1 \theta(t_2-t_1) V(t_2)V(t_1))\\ =& \frac{1}{2} \int_{-\infty}^{\infty}dt_1 dt_2 (\theta(t_1-t_2) V(t_1)V(t_2) + \theta(t_2-t_1) V(t_2)V(t_1))\\ =& \frac{1}{2} \int_{-\infty}^{\infty}dt_1 dt_2 T\{V(t_1)V(t_2)\}\\ \end{aligned}$

因此，散射矩阵可以写为：

$\begin{aligned} S &= 1 - i\int_{-\infty}^{\infty} dt_1T\{V_1(t)\} + \frac{(-i)^2}{2}\int_{-\infty}^{\infty} dt_1dt_2T\{V(t_1)V(t_2)\}\\ &\quad + \frac{(-i)^3}{3!}\int_{-\infty}^{\infty} dt_1dt_2dt_3 T\{V(t_1)V(t_2)V(t_3)\} + \cdots\\ &= 1 + \sum_{n=1}^{\infty} \frac{(-i)^n}{n!}\int_{-\infty}^{\infty}dt_1\cdots dt_n T\{V(t_1)\cdots V(t_n)\}\\ &=T\{\exp(-i\int_{-\infty}^{\infty}V(t) dt)\}\\ \end{aligned}\tag{16}$

考虑相互作用可以写为如下形式：

$V = \int d^3x \mathcal{H}(\bm{x},t) \tag{17}$

代入 $(16)$ 式得到：

$\begin{aligned} S &=1 + \sum_{n=1}^{\infty} \frac{(-i)^n}{n!}\int_{-\infty}^{\infty}d^4x_1\cdots d^4x_n T\{\mathcal{H}(\bm{x}_1,t_1)\cdots \mathcal{H}(\bm{x}_n,t_n)\}\\ &=T\{\exp(-i\int_{-\infty}^{\infty}\mathcal{H}(\bm{x},t) d^4 x)\}\\ \end{aligned}\tag{18}$

我们此时希望散射矩阵是洛伦兹不变的。在 $(18)$ 式中，除了时序符号外其余均是洛伦兹不变的。时序在洛伦兹变换下如何变换呢？对于类时间隔的事件来说，洛伦兹变换并不改变时序；对于类空间隔的事件来说，洛伦兹变换确实可能改变时序，但是并不应当影响上述时序积分的结果。这意味着：

$[\mathcal{H}(x),\mathcal{H}(x')] = 0,\quad \forall\ (x-x')^2 \geqslant 0 \tag{19}$

这正是我们之前介绍的 “因果性” 所给出的要求。

在这里我们额外说明：对散射矩阵的上述要求实际上是 簇分解定理 cluster decomposition theorem：即：不同实验室的散射实验结果不相互影响。这点是容易理解的，若我们用 $\alpha_A,\beta_A$ 表示 $A$ 实验室散射实验中的入射粒子与出射粒子的集合，用 $\alpha_B,\beta_B$ 表示 $B$ 实验室散射实验中的入射粒子与出射粒子的集合。所谓不同实验室：这一点实际上是指两个散射事件的间隔是类空的。那么簇分解定理可以写为：

$\begin{aligned} S_{\beta_A\beta_B\alpha_A\alpha_B} &= \langle \Psi^{-}_{\beta_A\beta_B} | \Psi^{+}_{\alpha_A\alpha_B}\rangle\\ &= (\langle \Psi^{-}_{\beta_A}| \otimes \langle\Psi^{-}_{\beta_B}|)(| \Psi^{+}_{\alpha_A}\rangle \otimes |\Psi^{+}_{\alpha_B}\rangle)\\ &= \langle \Psi^{-}_{\beta_A}|\Psi^{+}_{\alpha_A}\rangle \langle \Psi^{-}_{\beta_B}|\Psi^{+}_{\alpha_B}\rangle\\ &= S_{\beta_A\alpha_A}S_{\beta_B\alpha_B}\\ \end{aligned}$

即：

$S_{AB} = S_{A}S_{B}$

利用时序积分写为：

$\begin{aligned} &T\{\exp(-i\int_{-\infty}^{\infty}\mathcal{H}(x_A)\mathcal{H}(x_B) d^4 x_Ad^4 x_B)\}\\ =& T\{\exp(-i\int_{-\infty}^{\infty}\mathcal{H}(x_A) d^4 x_A)\} T\{\exp(-i\int_{-\infty}^{\infty}\mathcal{H}(x_B) d^4 x_B)\}\\ =& T\{\exp(-i\int_{-\infty}^{\infty}\mathcal{H}(x_A) d^4 x_A)\exp(-i\int_{-\infty}^{\infty}\mathcal{H}(x_B) d^4 x_B)\}\\ \end{aligned}$

该式只有在：

$[\mathcal{H}(x_A),\mathcal{H}(x_B)] = 0$

时成立。

给定入射态与散射态后，得到：

$S_{\beta\alpha} = \langle \Psi^{-}_{\beta} | T\exp(-i\int_{-\infty}^{\infty}V(t)dt) |\Psi^{+}_{\alpha}\rangle$

关联函数的微扰展开

我们现在介绍 关联函数 的微扰展开。例如：我们现在尝试对 $\phi^4$ 理论的 两点关联函数 进行计算：

$\langle \Omega | T\phi(x)\phi(y)|\Omega\rangle \tag{20}$

其中 $|\Omega\rangle$ 为引入相互作用之后的基态，与自由情形下的基态 $|0\rangle$ 相区分。$T$ 为 time-ordering 符号，将在之后介绍。关联函数可以理解为粒子在 $y$ 和 $x$ 之间传播/激发的概率幅。对于自由场论情况，它就是费曼传播子：

$\langle 0|T\phi(x)\phi(y)|0\rangle_{free} = D_F(x-y) = \int \frac{d^4p}{(2\pi)^4} \frac{ie^{-ip\cdot (x-y)}}{p^2-m^2+i\epsilon}\tag{21}$

$\phi^4$ 理论的哈密顿量为：

$H = H_{0} + H_{int} = H_{Klein-Gordon} + \int d^3x \frac{\lambda}{4!}\phi^4(\bm{x})\tag{22}$

相互作用项的影响分为两方面：

• 影响物理量的演化
  在海森堡绘景下，有：

$\phi(x) = e^{iHt}\phi(\bm{x})e^{-iHt}$

• 使得本征态发生变化

在微扰论中，我们试图利用自由场论情形下的算子与真空态 $|0\rangle$ 来表示考虑相互作用项后的场量 $\phi(x)$ 与基态 $|\Omega\rangle$。

在固定时刻 $t_0$，$\phi(t_0,x)$ 可以使用阶梯算子展开为：

$\phi(t_0,x) = \int \frac{d^3p}{(2\pi)^3} \frac{1}{\sqrt{2E_{\bm{p}}}}(a_{\bm{p}}e^{i\bm{p}\cdot\bm{x}}+a^\dagger_{\bm{p}}e^{-i\bm{p}\cdot\bm{x}}) \tag{23}$

现在计算 $\phi(t,x),t\neq t_0$：

$\phi(t,x) = e^{iH(t-t_0)}\phi(t_0,\bm{x})e^{-iH(t-t_0)} \tag{24}$

当 $\lambda = 0$ 时，有：

$\phi(t,x)|_{\lambda=0} = e^{iH_0(t-t_0)}\phi(t_0,\bm{x})e^{-iH_0(t-t_0)}\equiv \phi_I(t,x) \tag{25}$

因为 $H_0$ 是可以对角化的，那么 $\phi_I$ 可以表示为：

$\phi_I(t,x) = \int \frac{d^3p}{(2\pi)^3} \frac{1}{\sqrt{2E_{\bm{p}}}}(a_{\bm{p}}e^{-ip\cdot x}+a^\dagger_{\bm{p}}e^{ip\cdot x}) \tag{26}$

利用 $\phi_I(t,x)$ 我们可以得到 $\phi(t,x)$ 的表达式。

$\begin{aligned} \phi(x,t) &= e^{iH(t-t_0)}e^{-iH_0(t-t_0)}\phi_I(t,x)e^{iH_0(t-t_0)} e^{-iH(t-t_0)}\\ &\equiv U^\dagger(t,t_0)\phi_I(t,\bm{x})U(t,t_0) \end{aligned} \tag{27}$

其中 $U$ 是一个幺正算子：

$U(t,t_0) = e^{iH_0(t-t_0)} e^{-iH(t-t_0)} \tag{28}$

计算其随时演化的行为：

$\begin{aligned} i\frac{\partial}{\partial t}U(t,t_0) &= e^{iH_0(t-t_0)} (H-H_0)e^{-iH(t-t_0)}\\ &= e^{iH_0(t-t_0)} H_{int} e^{-iH_0(t-t_0)}e^{iH_0(t-t_0)}e^{-iH(t-t_0)}\\ &= H_I(t) U(t,t_0)\\ \end{aligned}\tag{28}$

其中：

$\begin{aligned} H_I(t) &= e^{iH_0(t-t_0)} H_{int} e^{-iH_0(t-t_0)}\\ &= \int d^3x\frac{\lambda}{4!}\phi_I^4\\ \end{aligned}\tag{29}$

与计算散射矩阵类似的，通过引入时序积分，我们得到：

$U(t,t_0) = T\{\exp(-i\int_{t_0}^{t}dt' H_I(t'))\}$

上述选取了一个参考时 $t_0$，一般来说有：

$U(t,t') = T\{\exp(-i\int_{t'}^{t}dt'' H_I(t''))\}\tag{30}$

其中：

$U(t,t') = U(t,0)U(0,t') = e^{iH_0t}e^{-iH(t-t')}e^{-iH_0t'} \tag{31}$

这与我们之前得到的时间演化算子的形式是一样的。

---

现在我们对基态 $|\Omega\rangle$ 做一些讨论。

考虑以下表达式，因为 $H$ 的本征态 $|n\rangle$ 构成一组完备基底，有：

$\begin{aligned} e^{-iHT}|0\rangle &= \sum_n e^{-iE_nT}|n\rangle\langle n|0\rangle \\ &= e^{-iE_0T}|\Omega\rangle\langle \Omega|0\rangle + \sum_{n\neq 0} e^{-iE_nT}|n\rangle\langle n|0\rangle \\ \end{aligned}$

取极限 $T\rightarrow \infty(1-i\epsilon)$，那么 $E_n>E_0$ 的项将趋于零，得到：

$\begin{aligned} |\Omega\rangle &= \lim_{T\rightarrow \infty(1-i\epsilon)}(e^{-iE_0T}\langle\Omega|0\rangle)^{-1} e^{-iHT}|0\rangle\\ &\overset{T\rightarrow T+t_0}{=} \lim_{T\rightarrow \infty(1-i\epsilon)}(e^{-iE_0(T+t_0)}\langle\Omega|0\rangle)^{-1} e^{-iH(T+t_0)}|0\rangle\\ &= \lim_{T\rightarrow \infty(1-i\epsilon)}(e^{-iE_0(t_0-(-T))}\langle\Omega|0\rangle)^{-1} e^{-iH(t_0-(-T))}e^{-iH_0(-T-t_0)}|0\rangle\\ &= \lim_{T\rightarrow \infty(1-i\epsilon)}(e^{-iE_0(t_0-(-T))}\langle\Omega|0\rangle)^{-1}U(t_0,-T)|0\rangle\\ \end{aligned}\tag{32}$

推导中用到：$H_0|0\rangle = 0$

类似的，得到：

$\begin{aligned} \langle\Omega| &= \lim_{T\rightarrow \infty(1-i\epsilon)}\langle 0|U(T,t_0)(e^{-iE_0(T-t_0)}\langle 0|\Omega\rangle)^{-1} \end{aligned}$

计算两点关联函数（假设 $x^0>y^0>t_0$）：

$\begin{aligned} \langle \Omega|\phi(x)\phi(y)|\Omega\rangle &= \lim_{T\rightarrow \infty(1-i\epsilon)}(e^{-iE_0(T-t_0)}\langle 0|\Omega\rangle)^{-1} \langle 0|U(T,t_0)\\ &\quad \times U^\dagger(x^0,t_0)\phi_I(x)U(x^0,t_0)U^\dagger(y^0,t_0)\phi_I(y)U(y^0,t_0)\\ &\quad \times U(t_0,-T)|0\rangle(e^{-iE_0(t_0-(-T))}\langle\Omega|0\rangle)^{-1}\\ &= \lim_{T\rightarrow \infty(1-i\epsilon)} (|\langle 0|\Omega\rangle|^2e^{-2iE_0T})^{-1}\langle 0|U(T,x^0)\phi_I(x)U(x^0,y^0)\phi_I(y)U(y^0,-T)|0\rangle \end{aligned}$

考虑到：

$\begin{aligned} 1 &= \langle \Omega|\Omega\rangle\\ &= \lim_{T\rightarrow \infty(1-i\epsilon)} (|\langle 0|\Omega\rangle|^2e^{-2iE_0T})^{-1}\langle 0|U(T,t_0)U(t_0,-T)|0\rangle\\ &=\lim_{T\rightarrow \infty(1-i\epsilon)} (|\langle 0|\Omega\rangle|^2e^{-2iE_0T})^{-1}\langle 0|U(T,-T)|0\rangle\\ \end{aligned}$

如此，关联函数可以改写为：

$\begin{aligned} \langle \Omega|\phi(x)\phi(y)|\Omega\rangle &= \lim_{T\rightarrow \infty(1-i\epsilon)}\frac{\langle 0|U(T,x^0)\phi_I(x)U(x^0,y^0)\phi_I(y)U(y^0,-T)|0\rangle}{\langle 0|U(T,-T)|0\rangle} \end{aligned}$

注意到，上述式子中的 $U,\phi$ 均按照时间顺序从大到小排列。引入时序积分符号，可以将关联函数写为：

$\begin{aligned} \langle \Omega|T\{\phi(x)\phi(y)\}|\Omega\rangle = \lim_{T\rightarrow \infty(1-i\epsilon)}\frac{\langle 0|T\{\phi_I(x)\phi_I(y)\exp(-i\int_{-T}^{T}dtH_I(t))|0\rangle}{\langle 0|T\{\exp(-i\int_{-T}^{T}dtH_I(t))\}|0\rangle} \end{aligned}\tag{33}$

或者直接写为：

$\begin{aligned} \langle \Omega|T\{\phi(x)\phi(y)\}|\Omega\rangle = \frac{\langle 0|T\{\phi_I(x)\phi_I(y)\exp(-i\int_{-\infty}^{\infty}dtH_I(t))|0\rangle}{\langle 0|T\{\exp(-i\int_{-\infty}^{\infty}dtH_I(t))\}|0\rangle} \end{aligned}\tag{34}$

Wick 定理

在得到散射矩阵与关联函数的微扰展开式后，现在考虑如何进行具体的计算。现在我们介绍 wick 定理。

我们将 $\phi_I(x)$ 分解为正频项与负频项：

$\phi_I(x) = \phi^{+}_I(x)+\phi^{-}_I(x)$

其中有：

$\begin{aligned} &\phi^{+}_{I}(x) = \int \frac{d^3p}{(2\pi)^3}\frac{1}{\sqrt{2E_{\bm{p}}}}a_{\bm{p}}e^{-ip\cdot x}\\ &\phi^{-}_{I}(x) = \int \frac{d^3p}{(2\pi)^3}\frac{1}{\sqrt{2E_{\bm{p}}}}a^\dagger_{\bm{p}}e^{ip\cdot x}\\ \end{aligned}$

我们计算时序积：

$\begin{aligned} T\phi_I(x)\phi_I(y) &\underset{x^0 > y^0}{=} \phi_I^{+}(x)\phi^{+}_I(y) + \phi_I^{+}(x)\phi_I^{-}(y) + \phi_I^{-}(x)\phi_I^{+}(y) + \phi_I^{-}(x)\phi_I^{-}(y)\\ &= \phi_I^{+}(x)\phi^{+}_I(y) + \phi_I^{-}(y)\phi_I^{+}(x) + \phi_I^{-}(x)\phi_I^{+}(y) + \phi_I^{-}(x)\phi_I^{-}(y) + [\phi_{I}^+(x),\phi_{I}^-(y)]\\ \end{aligned}$

如此，除了对易项之外，所有的项内的阶梯算子乘积项都是 “正规序”，即所有湮灭算子在产生算子右边。我们定义 $N()$ 符号将一个阶梯算子的乘积表示为正规序。那么有例子：

$N(a_{\bm{p}}a_{\bm{k}}^\dagger a_{\bm{q}}) = a_{\bm{k}}^\dagger a_{\bm{p}} a_{\bm{q}}$

对于 $x^0<y^0$ 的情况，上式中只有对易项不同，为 $[\phi_{I}^+(y),\phi_{I}^-(x)]$。为了统一表示，我们定义两个场量的 缩并 contraction：

在 Peskin, An introduction to Quantum Field Theory 中使用折线表示缩并，但那种方法的符号较难在 markdown 中写出，我们使用 wiki 中引入的符号：同样的上标表示进行缩并。

$\begin{aligned} \phi^{\bullet}(x)\phi^{\bullet}(y) &= \left\{\begin{aligned} [\phi^+(x),\phi^{-}(y)],\quad x^0>y^0\\ [\phi^+(y),\phi^{-}(x)],\quad x^0<y^0\\ \end{aligned}\right.\\ &= D_F(x-y)\\ \end{aligned}\tag{35}$

那么可以将时序积表示为：

$T\{\phi(x)\phi(y)\} = N\{\phi(x)\phi(y) + \phi^{\bullet}(x)\phi^{\bullet}(y)\}$

对于更复杂的时序积 $T\{\phi(x_1)\phi(x_2)\cdots\phi(x_m)\}$ 应当表示为 $\phi(x_1)\phi(x_2)\cdots\phi(x_m)$ 的所有可能的缩并的总和，再写为正规序，这就是 wick 定理。例如：

$\begin{aligned} T\{\phi_1\phi_2\phi_3\phi_4\} = N\{\phi_1\phi_2\phi_3\phi_4&+\phi^\bullet_1\phi^\bullet_2\phi_3\phi_4 + \phi^\bullet_1\phi_2\phi_3^\bullet\phi_4 + \phi^\bullet_1\phi_2\phi_3\phi_4^\bullet\\ &+\phi_1\phi^\bullet_2\phi^\bullet_3\phi_4 + \phi_1\phi_2^\bullet\phi_3\phi_4^\bullet + \phi_1\phi_2\phi_3^\bullet\phi_4^\bullet\\ &+\phi^\bullet_1\phi^\bullet_2\phi^{\bullet\bullet}_3\phi^{\bullet\bullet}_4 + \phi^\bullet_1\phi^{\bullet\bullet}_2\phi^\bullet_3\phi^{\bullet\bullet}_4 + \phi^\bullet_1\phi^{\bullet\bullet}_2\phi^{\bullet\bullet}_3\phi^\bullet_4\}\\ \end{aligned}$

这里 $\phi_a$ 是 $\phi(x_a)$ 的简写。

场量缩并可以使用费曼传播子表示，例如：

$N\{\phi^\bullet_1\phi^\bullet_2\phi_3\phi_4\} = D_F(x_1-x_2)\cdot N\{\phi_3\phi_4\}$

显然：一个具有正规序的场量乘积对真空态的期望值为零：

$\langle 0| N\{\cdots\}|0\rangle = 0$

可得：

$\begin{aligned} \langle 0|T\{\phi_1\phi_2\phi_3\phi_4\}|0\rangle &= D_F(x_1-x_2)D_F(x_3-x_4)\\ & + D_F(x_1-x_3)D_F(x_2-x_4)\\ & + D_F(x_1-x_4)D_F(x_2-x_3)\\ \end{aligned}$

现在使用数学归纳法证明 wick 定理：
在 $m=2$ 时，即只有两个场量时，wick 定理显然成立。
假设对于共有 $m-1$ 个场时，wick 定理成立。不失一般性的，我们令 $x_1^0 \geqslant x_2^0 \geqslant \cdots \geqslant x_m^0$，现在对于 $\phi_2,\cdots \phi_m$ 应用 wick 定理。得到：

$\begin{aligned} T\{\phi_1\cdots\phi_m\} &= \phi_1\cdots\phi_m\\ &= \phi_1 T\{\phi_2\cdots\phi_m\}\\ &= \phi_1 N\{\phi_2\cdots\phi_m + \left\{\begin{aligned}&all\ contractions\ \\ & not\ involving\ \phi_1\\ \end{aligned}\right\} \}\\ &= (\phi_1^+ + \phi_1^-) N\{\phi_2\cdots\phi_m +\left\{\begin{aligned}&all\ contractions\ \\ & not\ involving\ \phi_1\\ \end{aligned}\right\} \}\\ \end{aligned}$

其中：

$\begin{aligned} \phi_1^{-}N\{\phi_2\cdots \phi_m\} &= N\{\phi_1^{-}\phi_2\cdots \phi_m\}\\ \phi_1^{+}N\{\phi_2\cdots \phi_m\} &= N\{\phi_2\cdots \phi_m\}\phi_1^{+} + [\phi_1^+,N\{\phi_2\cdots \phi_m\}]\\ &= N\{\phi_1^{+}\phi_2\cdots \phi_m\} + N\{[\phi_1^+,\phi_2^{-}] \cdots \phi_m\} + \cdots + N\{\phi_2 \cdots [\phi_1^+,\phi_m^{-}]\}\\ & = N\{\phi_1^+\phi_2\cdots\phi_m +\left\{\begin{aligned}&all\ contractions\ \\ & involving\ \phi_1\\ \end{aligned}\right\} \}\\ \end{aligned}$

综上可得：

$T\{\phi_1\cdots\phi_m\} = N\{\phi_1\phi_2\cdots\phi_m +\left\{\begin{aligned}&all\ possible\ \\ & contractions \\ \end{aligned}\right\} \}$

那么如何使用 wick 定理去计算散射矩阵与关联函数呢？Feynman 使用了图形化的语言完成了这件事情，我们将在下一篇中做这件有趣的事。