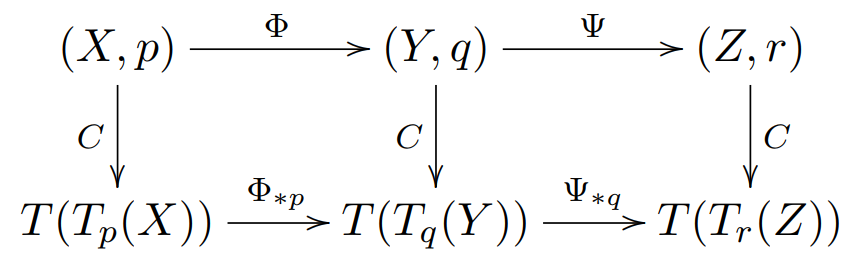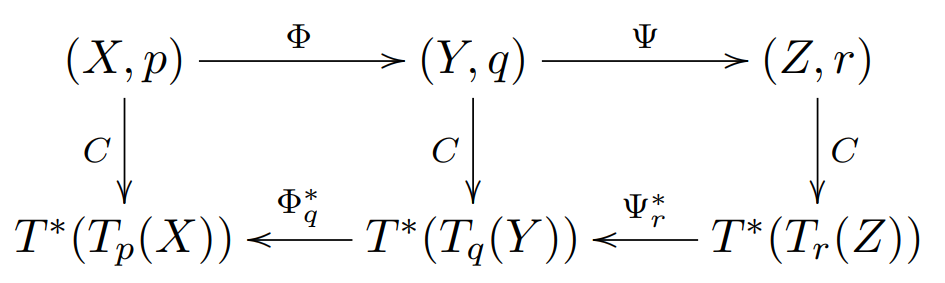广义相对论的数学基础（十二）：张量场

张量场

一点处的张量

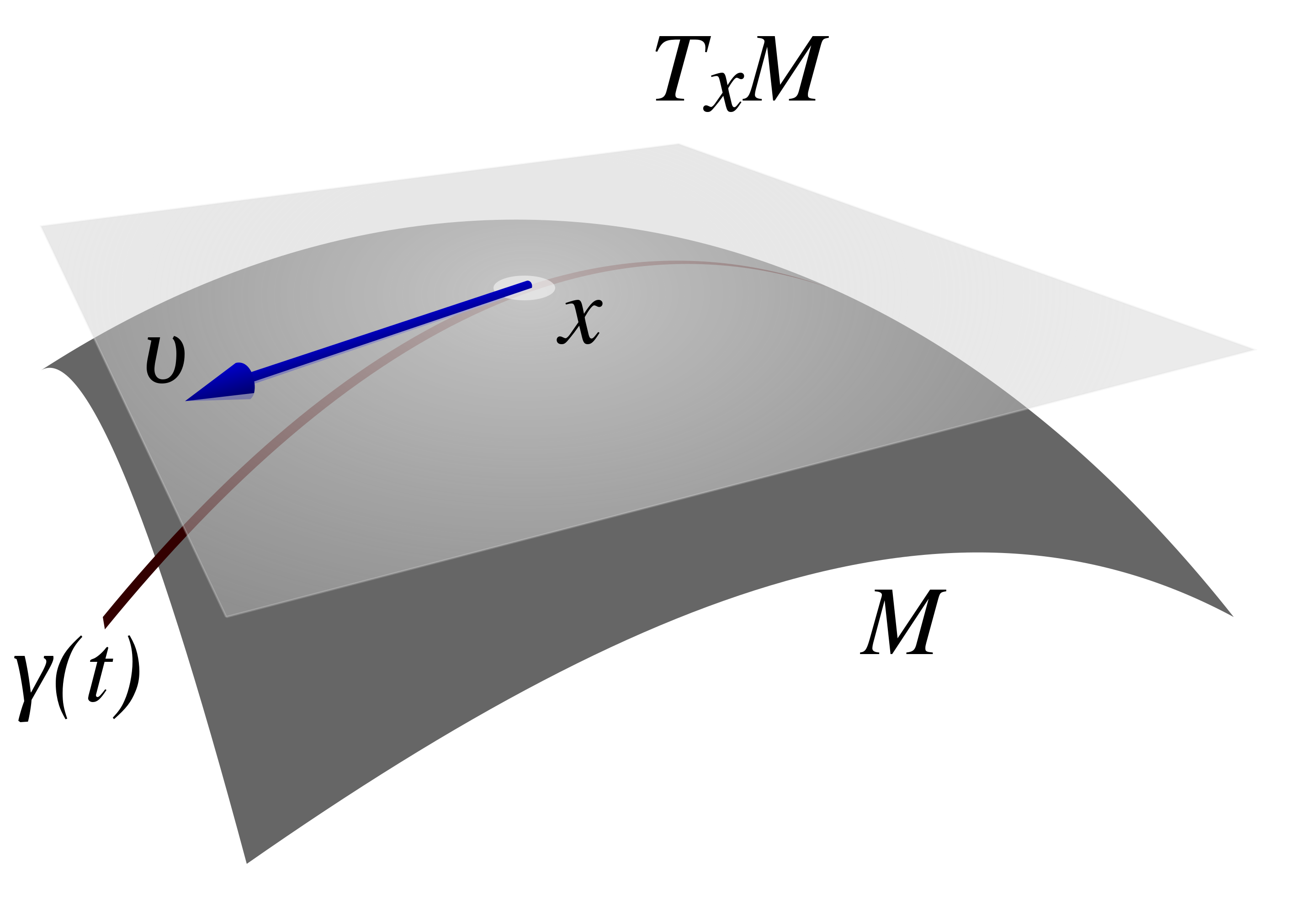
我们在上一篇中知道了：对于流形 $X$ 上的任意一点 $p$ ，有相应的切空间 $T_pX$ 和余切空间 $T_p^*X$ ，它们的维数和流形的维数一致。而且它们的基底分别为：

$\{e_i = \frac{\partial}{\partial x^i}|_p,i=1,\cdots,n\}\quad and\quad \{e^{*i} = dx^i|_p,i=1,\cdots,n\}$

由此我们可以在 $p$ 点定义张量，得到 $(r,s)$ -型张量所形成的线性空间

$T^r_s(p)=\underbrace{T_pX\otimes\cdots\otimes T_pX}_{r}\otimes\underbrace{T^* _ pX\otimes\cdots\otimes T^* _ pX}_{s}$

在某个坐标卡的自然基下，任意一个 $p$ 点的 $(r,s)$ -型张量 $t_p$ 可以展开为：

$t_p = (t_p )^{i_1 \cdots i_r}_{\qquad j_1 \cdots j_s} e_{i_1} \otimes \cdots \otimes e_{i_r} \otimes e^{* j_1} \otimes \cdots \otimes e^{* j_s}$

推前映射

我们在介绍流形间的光滑映射时已经提到了关于光滑函数的拖回映射，并说明了它是光滑流形范畴和线性空间范畴间的一个逆变函子。现在我们来讨论一点处张量的推前和拖回映射。

一点处张量的推前(push forward)
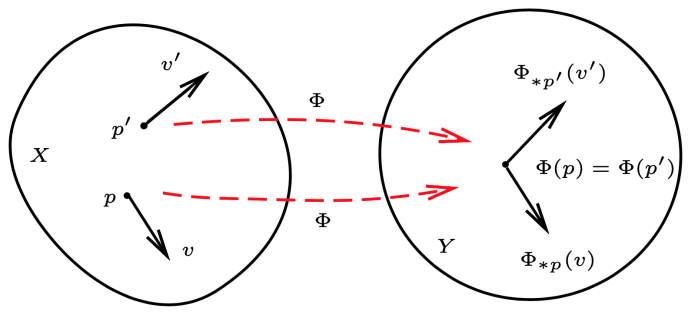
设 $v \in T_p X$ ， $p$ 点的推前映射是一个由 $p$ 点的切空间到 $q = \Phi(p)$ 点的切空间 $T_q Y$ 的映射：

$\Phi_{*p} : T_p X \rightarrow T_q Y , v \mapsto \Phi_{*p}(v)$

定义为：

$\Phi_{*p} (v)(g) = v(\Phi^* g), \forall g \in\mathscr{F}(Y )$

对于映射 $\Phi: X\rightarrow Y$ ， $\Phi^*$ 为 $\Phi$ 诱导出的 $\mathscr{F}(Y) \rightarrow \mathscr{F}(X)$ 的拖回映射：

$\forall g\in \mathscr{F}(Y),\ \forall p\in X\quad \Phi^*(g)(v) := g\circ\Phi(p)$

$\Phi_{*p}$ 是 $T_p X$ 上的一个线性映射。 $\forall g\in \mathscr{F}(Y)$ ，那么 $\Phi^*g \in \mathscr{F}(X)$ ， $v(\Phi^* g) \in \mathbb{R}$ ，来考虑 $\Phi_{*p}(v)$ 将 $Y$ 上的光滑函数 $g$ 映成实数，并且是线性映射，因此其应当是 $q = \Phi(p)\in Y$ 点的切矢量。即： $\Phi_{*p}(v) \in T_qY$ 。

我们称 $\Phi_{*p}$ 为 $\Phi$ 在 $p$ 点的“推前映射”或“切映射”。它将 $p$ 点的切矢量变成 $q = \Phi(p)$ 点的切矢量。

可以将推前映射扩张到整个逆变张量代数 $T(T_pX)$ ，使得：

$\Phi_{*p}(x\otimes y) = \Phi_{*p}(x) \otimes \Phi_{*p}(y),\quad \forall x,y\in T(T_pX)$

可以看出上述过程具有协变函子的特征。可以用以下交换图表示：

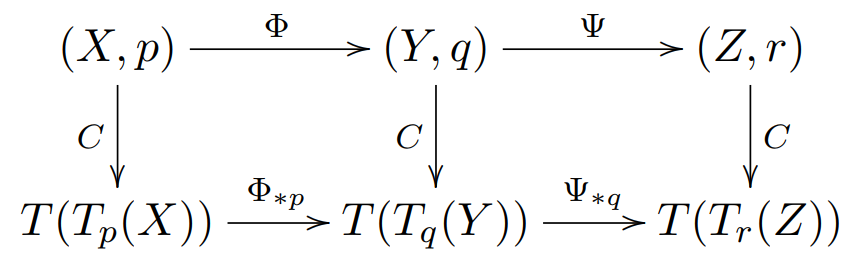
其中：

$q = \Phi(p),\quad r=\Psi\circ\Phi(p)$

另外，我们有：

$(\Psi\circ\Phi)_{*p} = \Psi_{*q}\circ \Phi_{*p}$

为了能更好地理解一点处张量场地推前，我们考虑它在坐标系下地表述：
设 $(U,\varphi)$ 是 $X$ 上包含 $p$ 点的坐标卡，相应的坐标为 $\{x^i,i=1,\cdots,n\}$ ，自然基和其对偶基分别为：

$\frac{\partial}{\partial x^i}|_p\quad dx^i|_p\quad i=1,\cdots,n$

设 $(V,\psi)$ 是 $Y$ 上包含 $q$ 点的坐标卡，相应的坐标为 $\{y^I,I=1,\cdots,m\}$ ，自然基和其对偶基分别为：

$\frac{\partial}{\partial y^I}|_q\quad dy^I|_q\quad i=1,\cdots,m$

下面我们考虑自然基的推前，即：

$\Phi_{*p}\frac{\partial}{\partial x^i}|_p$

这应当是一个 $q$ 点的切矢量，因此可以在基底 $\frac{\partial}{\partial y^I}$ 下展开。其展开系数为：

$\begin{aligned} \Phi_{*p}\frac{\partial}{\partial x^i}|_p(y^I) &= \frac{\partial}{\partial x^i}|_p (\Phi^*y^I)\\ &= \frac{\partial}{\partial x^i}|_p (y^I\circ\Phi)\\ &= \frac{\partial (y^I \circ \Phi \circ \varphi^{-1})}{\partial x^i}|_{\varphi(p)}\\ &= \frac{\partial (y^I \circ \psi^{-1}(\psi \circ \Phi \circ \varphi^{-1}))}{\partial x^i}|_{\varphi(p)}\\ \end{aligned}$

即有：

$\Phi_{*p}\frac{\partial}{\partial x^i}|_p = \frac{\partial y^I}{\partial x^i}\frac{\partial}{\partial y^I}|_{q}$

其中：

$\frac{\partial y^I}{\partial x^i} = \frac{\partial (y^I \circ \psi^{-1}(\psi \circ \Phi \circ \varphi^{-1}))}{\partial x^i}|_{\varphi(p)}$

对于任意一个 $(r,0)$ -型张量 $t_p$ ：

$t_p = t_p^{i_1\cdots i_r} \frac{\partial}{\partial x^{i_1}}|_p\otimes \cdots \otimes \frac{\partial}{\partial x^{i_r}}|_p$

可以得到：

$\Phi_{*p}t_p = t_p^{i_1\cdots i_r}\frac{\partial y^{I_1}}{\partial x^{i_1}}\cdots \frac{\partial y^{I_r}}{\partial x^{i_r}} \frac{\partial}{\partial y^{I_1}}|_p\otimes \cdots \otimes \frac{\partial}{\partial y^{I_r}}|_p$

拖回映射

一点处张量的拖回 (pull back)
推前的转置给出对偶空间 $T^*_qY$ 到对偶空间 $T^*_ p X$ 的一个线性映射。我们记这个线性映射为 $\Phi^ *_q$ ，其具体定义如下：

$\Phi^*_q (\omega) = \omega \circ \Phi_{*p} ,\ \forall \omega \in T^*_ q Y$

可以给出有关拖回映射的如下交换图：

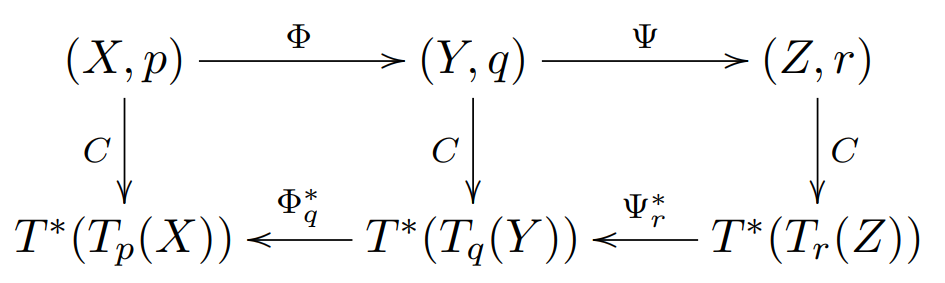
其中的拖回映射的复合满足：

$(\Psi\circ\Phi)_{r}^* = \Phi_q^*\circ \Psi_r^*$

这样我们得到了两个范畴之间的一个逆变函子。

类似于推前的情况，我们可以得到拖回映射在基底下的表示：

$\Phi_q^*dy^I = \frac{\partial y^I}{\partial x^i}dx^i|_p$

我们可以将拖回映射扩张到整个协变张量代数 $T (T^*_ pX)$ 。

特殊地，当 $\Phi : X \rightarrow Y$ 是微分同胚时，可以证明 $\Phi_{* p}$ 是同构映射. 因此它存在逆，由此我们可以考虑这个逆映射的拖回。而对协变张量拖回映射能够很好地定义。这样按照我们前面关于同构映射张量积的讨论，我们可以将这个推前映射推广到整个张量代数 $\mathcal{T}(T_p X)$ 。

张量场

张量场粗略的说就是在流形的每一点上指定一个张量。

光滑流形 $X$ 上的 $(r,s)$ -型 光滑张量场 (smooth tensor field) $t$ 是指在 $X$ 的每一点都指定一个 $(r,s)$ -型张量 $t_p$ 。并且，对于每一点 $p \in X$ ，都有一个局部坐标系 $(U,\varphi)$ 使得 $t$ 可表示为：

$t = t^{i_1 \cdots i_r}_{\qquad j_ 1 \cdots j_ s}\frac{\partial}{\partial x^{i_1}} \otimes\cdots\otimes\frac{\partial}{\partial x^{i_r}}\otimes dx^{j_1} \otimes\cdots \otimes dx^{j_s}$

其中 $t^{i_1 \cdots i_r}_{\qquad j_ 1 \cdots j_ s}$ 是坐标域 $U$ 上的光滑函数。

使用抽象指标，可以将光滑张量场 $t$ 记为：

$t^{a_1\cdots a_r}_{\qquad b_1\cdots b_s}$

这个表达式是不依赖于基底选取的，张量场也是不依赖于基底的。

$(0,0)$ -型张量场就是流形上的 光滑函数，所有光滑函数的集合记为 $\mathscr{F}(X)$ 。
$(1,0)$ -型光滑张量场称为 $X$ 上的 光滑切矢量场。所有光滑切矢量场的集合通常记为 $\mathscr{X} (X)$ 。
$(0,1)$ -型光滑张量场也称为 $1$ -形式场。所有 $1$ -形式场的集合通常记为 $\Lambda_1 (X)$ 。
我们用 $\mathscr{T}^r_s(X)$ 表示流形 $X$ 上所有光滑 $(r,s)$ -型张量场的集合。于是得到：

$\mathscr{F}(X) = \mathscr{T}_{0}^{0};\quad \mathscr{X}(X) = \mathscr{T}_{0}^{1};\quad \Lambda_1(X)=\mathscr{T}_{1}^{0}$

在一点处张量的引入中，光滑流形 $X$ 上 $p$ 点的 $(r,s)$ -型张量 $t_p$ 是一个 $(r+s)$ -重线性函数：

$t_p:\underbrace{T_p^*X\times\cdots\times T_p^*X}_{r}\times\underbrace{T_pX\times\cdots\times T_pX}_{s} \rightarrow \mathbb{R}$

那么流形 $X$ 上的 $(r,s)$ -型光滑张量场 $t$ 是如下 $(r+s)$ -重线性映射：

$t:\underbrace{\Lambda_1(X)\times\cdots\times \Lambda_1(X)}_{r}\times\underbrace{\mathscr{X}(X)\times\cdots\times \mathscr{X}(X)}_{s} \rightarrow \mathscr{F}(X)$

即：流形 $X$ 上 $(r,s)$ -型光滑张量场可以定义为 $\mathscr{F}(X)$ 取值的 $(r+s)$ -重线性映射，且对于每个变量是 $\mathscr{F}(X)$ -线性的。

我们之前已经在流形的每一点上构造出了所谓的张量代数，现在把直和与张量积进行逐点的推广，我们可以得到 张量场模：

$\mathscr{T}(X)=\bigoplus_{r,s=0}^\infty \mathscr{T}_s^r(X)$

形成环 $\mathscr{F}(X)$ 上的模。

张量场的推前与拖回

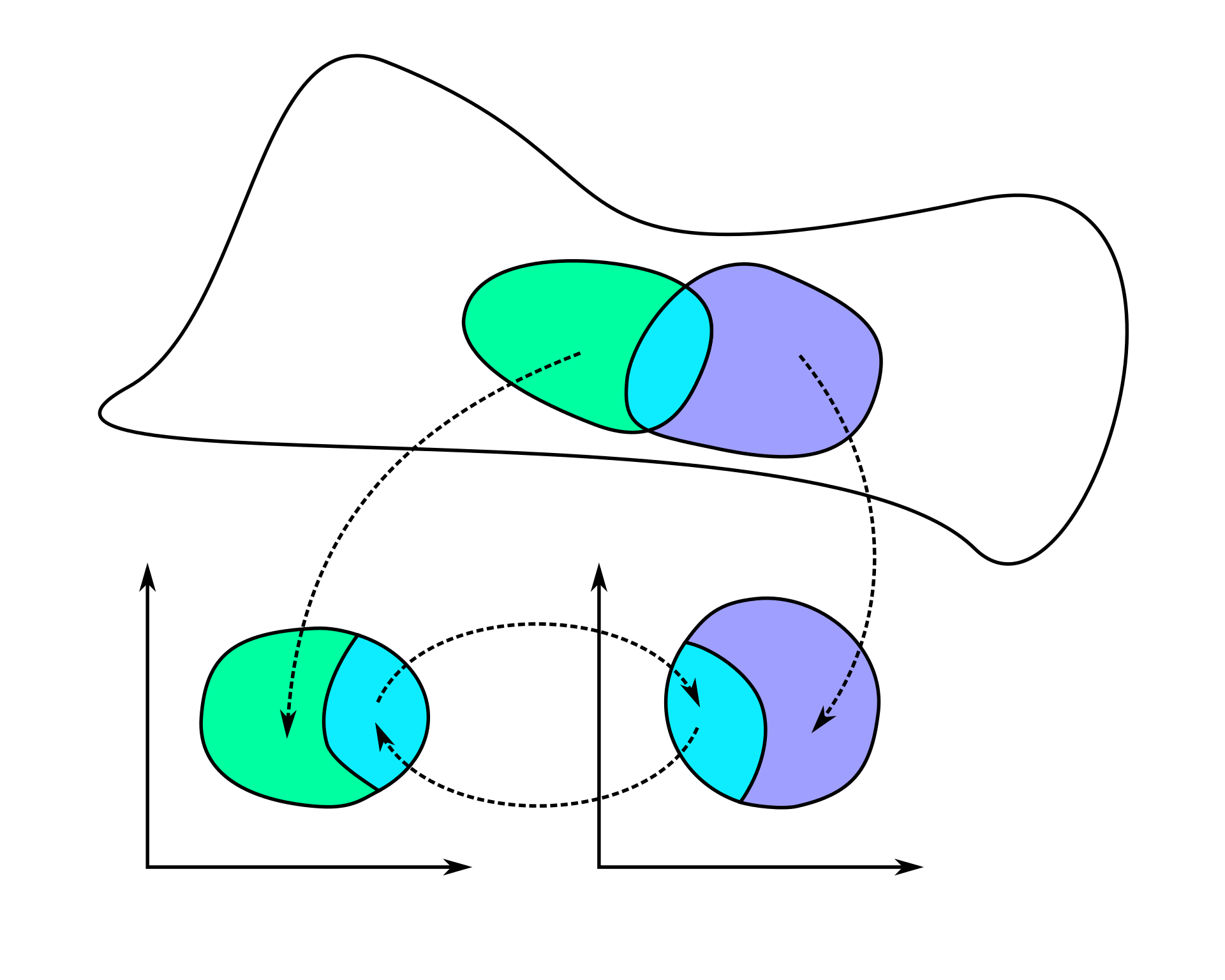
我们是否可以将推前映射也逐点地推广到一个一般的逆变光滑张量场呢？一般情况下，答案是否定的。

不难有以下观察：

非单射的情况
当映射 $\Phi$ $X\rightarrow Y$ 是多对一的情况，若 $X$ 上的矢量场在 $p$ 和 $p'$ 点的矢量被映为 $Y$ 在 $\Phi(p)$ 点的两个矢量。这样 $\Phi(p)$ 点被我们这个假定的推前映射指定了两个矢量，不能够在 $Y$ 上形成矢量场。

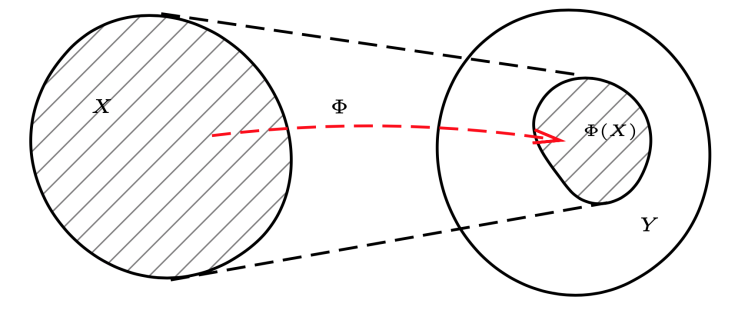
非满射的情况
若 $\Phi$ 不是满射，至多给出 $\Phi(X)$ 上的矢量场。

对于拖回映射，我们可以逐点地将拖回映射推广到光滑的协变张量场。

$\Phi^*: \mathscr{T}_s^0(Y) \rightarrow \mathscr{T}_s^0(X)$

若这两个流形是微分同胚的，这时我们可以逐点定义它的推前映射 $\Phi_*$ 。更进一步的，对于 $(0,s)$ -型张量，我们可以定义：

$\Phi_* := (\Phi^{-1})^*$

切矢量场

现在我们考虑光滑流形 $X$ 上的光滑切矢量场的集合 $\mathscr{X}(X)$ 。它是实数域 $\mathbb{R}$ 上的线性空间，也是光滑函数环 $\mathscr{F}(X)$ 上的模。另外，我们知道 $X$ 上任意一点 $p$ 处的切矢量 $v_p$ 是一个导子，即：

$v_p : \mathscr{F}(X) \rightarrow \mathbb{R}$

满足 $\mathbb{R}$ - 线性和 Leibniz 法则。光滑切矢量场在 $X$ 的每一点（光滑地）指定了一个切矢。因此光滑切矢量场 $v$ 形成了 $\mathscr{F}(X)$ 到 $\mathscr{F}(X)$ 的一个映射，这可以看作矢量场的另一种定义，即我们有：

$v : \mathscr{F}(X) \rightarrow \mathscr{F}(X),$

容易验证，光滑切矢量场满足 $\mathbb{R}$ -线性与 Leibniz 律。反之，满足 $\mathbb{R}$ -线性与 Leibniz 律的 $\mathscr{F}(X)\rightarrow \mathscr{F}(X)$ 映射为光滑切矢量场。

李括号

设 $u,v\in\mathscr{X}(X)$ ，它们也可以看作映射： $\mathscr{F}(X) \rightarrow \mathscr{F}(X)$ 。复合映射 $u\circ v$ 也是 $\mathscr{F}(X) \rightarrow \mathscr{F}(X)$ 的映射，但其并不满足 Leibniz 法则：

$\begin{aligned} (u\circ v)(fg) &= u(v(fg)) = u(fv(g)+ gv(f))\\ &= f(u\circ v)(g) + f(u\circ v)(g) + u(g)v(f) u(f)v(g)\\ \end{aligned}$

因此 $u\circ v$ 不是 $X$ 上的切矢量场（虽然满足 $\mathbb{R}$ -线性，但不满足 Leibniz 法则），所以 $u\circ v\notin \mathscr{X}(X)$ 。

我们定义如下矢量场的 李括号：

$[u,v] = u \circ v - v \circ u$

容易发现 $[u,v]$ 是 $X$ 上的切矢量场。

李括号具有的性质：

分配律

$\begin{aligned} [\lambda_1u_1 + \lambda_2u_2,v] &= \lambda_1[u_1,v] + \lambda_2[u_2,v]\\ [u,\lambda_1v_1 + \lambda_2v_2] &= \lambda_1[u,v_1] + \lambda_2[u,v_2]\\ \end{aligned}$