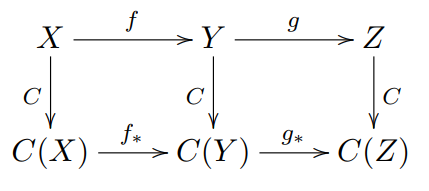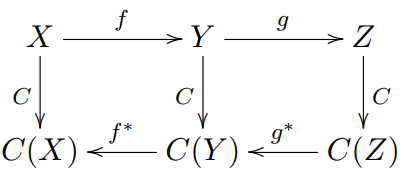广义相对论的数学基础（二）：范畴与关系

范畴

范畴论 (Category theory) 是数学的一门学科，以抽象的方法处理数学概念，将这些概念形式化成一组组的“对象”及“态射”。数学中许多重要的领域可以形式化为范畴。使用范畴论可以令这些领域中许多难理解、难捉摸的数学结论更容易叙述证明。

范畴的概念

在范畴论中，范畴 (category) 代表着一堆数学实体和存在于这些实体间的关系。

一个范畴 $\mathcal{C}$ 包含如下内容：

• 一个由一些 对象 (objects) 所构成的类 $\mathrm{ob} (\mathcal{C})$

• 对象间的 态射(morphism) 所构成的类 $\mathrm{Hom} (\mathcal{C})$

  态射是指从一个“源物件”对象 $a$ 到“目标对象” $b$ 的映射 $f:a\mapsto b$，其中 $a,b\in\mathrm{ob} (\mathcal{C})$。所有从 $a$ 到 $b$ 的态射组成的类称为 态射类，记为 $\mathrm{Hom} (a,b)$

• 对任三个对象 $a,b,c$，有二元运算：

$\mathrm{Hom} (a,b)\times\mathrm{Hom} (b,c)\rightarrow \mathrm{Hom} (a,c)$

称为 态射的复合。该二元运算将满足如下两个条件：

• 结合律
  若 $f \in \mathrm{Hom} (a,b), g \in \mathrm{Hom} (b,c),h \in \mathrm{Hom} (c,d)$，则：

$h\circ (g\circ f) = (h\circ g)\circ f$

• 存在 恒等态射
  对任意一个对象 $a$，$\mathrm{Hom} (a,a)$ 中存在唯一元素，记为 $\mathrm{Id}_a$，使得:

  $\begin{aligned} &f\circ \mathrm{Id}_a = f,\ \forall f \in \mathrm{Hom} (a,b)\\ &\mathrm{Id}_a \circ g = g,\ \forall g \in \mathrm{Hom} (b,a)\\ \end{aligned}$

同构态射 (isomorphism)
一个态射 $f ∈ \mathrm{Hom} (a,b)$ 称为 同构，若存在一个 $g\in \mathrm{Hom} (b,a)$，使得：

$f\circ g = \mathrm{Id}_b,\ g\circ f = \mathrm{Id}_a .$

如何将范畴的概念对应到具体实体中呢？我们举一个例子：
以集合为对象，以集合之间的映射为态射。那么态射的复合是很好定义的，且满足上述提到的两点性质。我们可以说：则所有的集合与它们之间的映射形成一个范畴。这时候集合间的双射就是同构态射。

通常我们将一个范畴记为 $(\mathscr{A},\mathrm{Mor}(\mathscr{A}))$，其中 $\mathscr{A}$ 表示一个类，$\mathrm{Mor}(\mathscr{A})$ 表示其上的所有态射。

函子

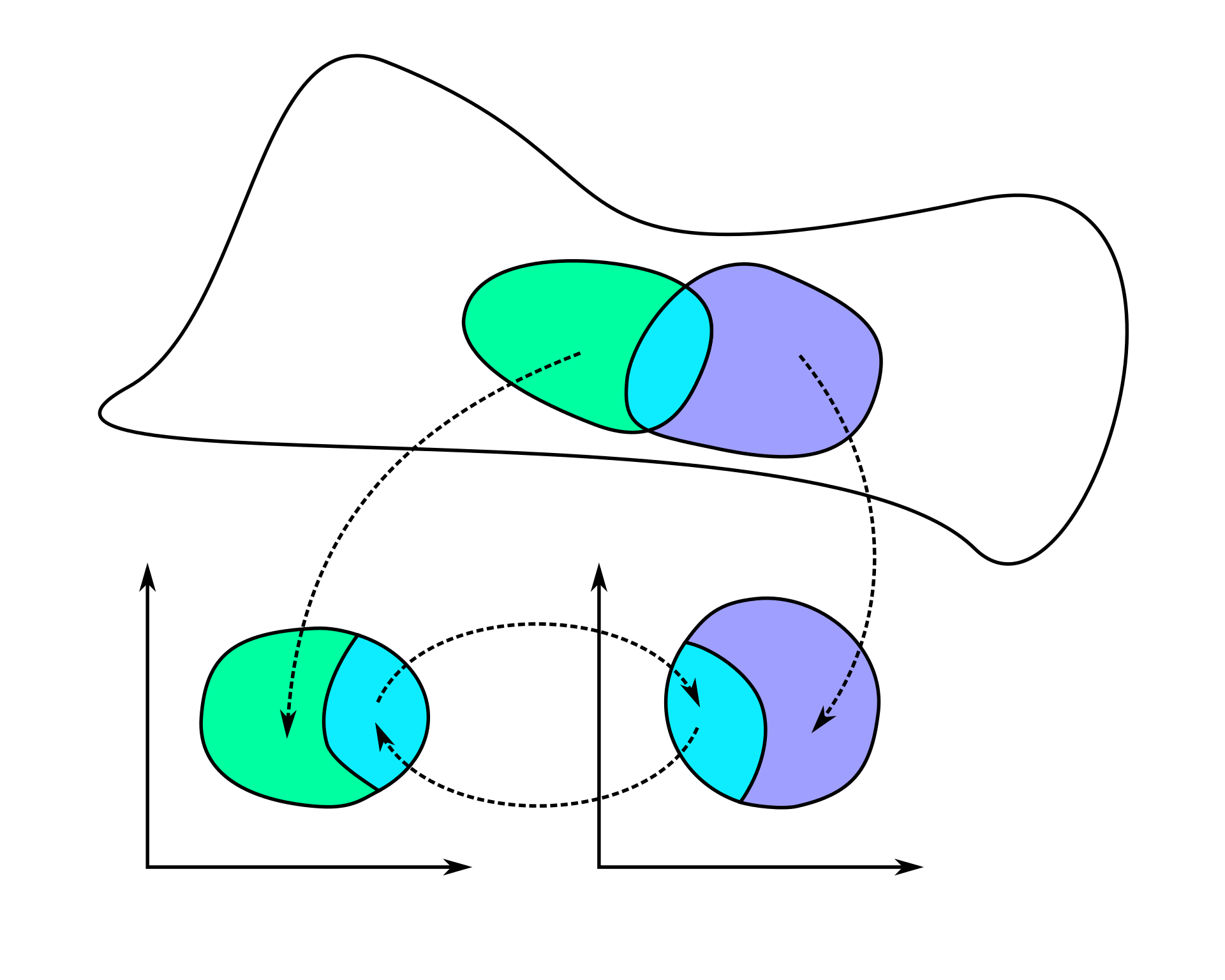
利用函子，我们可以描述不同数学实体之间的关系。在范畴论中，函子 (functor) 是范畴间的一类映射。

设 $(\mathscr{A},\mathrm{Mor}(\mathscr{A}))$ 与 $(\mathscr{B},\mathrm{Mor}(\mathscr{B}))$ 为范畴，从 $(\mathscr{A},\mathrm{Mor}(\mathscr{A}))$ 到 $(\mathscr{B},\mathrm{Mor}(\mathscr{B}))$ 的函子是一个映射 $C$：

$C: (\mathscr{A},\mathrm{Mor}(\mathscr{A})) \rightarrow (\mathscr{B},\mathrm{Mor}(\mathscr{B}))$

$C$ 是一个范畴间的映射。
它可以将一个对象映射成另一个对象：若 $X \in \mathscr{A}$，则有 $C(X) \in \mathscr{B}$
可以将一个态射映射成另一个态射：若 $f \in \mathrm{Mor}(\mathscr{A})$，则有 $C(f) \in \mathrm{Mor}(\mathscr{B})$

并且要求具有以下性质：

• 若 $f: X \rightarrow Y$ 是一个态射，那么 $C(f)$ 为如下态射：

$C(f):C(X)\rightarrow C(Y)$

• 若 $f,g\in\mathrm{Mor}(\mathscr{A})$，且它们可以复合，则有：

$C(f)\circ C(g) = C(f\circ g)$

• 保持恒元：

$C(\mathrm{Id}_X) = \mathrm{Id}_{C(X)}$

按照以上定义的函子又称为 协变函子 (covariant functor)，通常我们将 $C (f)$ 记为 $f_∗$。

我们可以用以下示意图理解协变函子的性质：

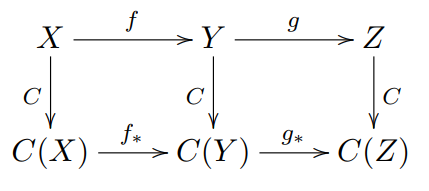
我们还有 逆变函子 (contravariant functor)。与协变函子唯一不同的是，逆变函子的态射复合定义为：

• 若 $f,g\in\mathrm{Mor}(\mathscr{A})$，且它们可以复合，则有：

$C(f)\circ C(g) = C(g\circ f)$

对于逆变函子，我们将 $C(f)$ 记为 $f^*$。我们可以用以下示意图理解协变函子的性质：

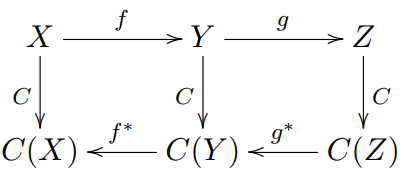
关系

关系 (relations)
两个集合 $X$ 和 $Y$ 之间的关系 $R$ 是卡氏积 $X\times Y$ 的一个子集。
若 $ (x,y) ∈ R$，则称 $x \in X$ 和 $y \in Y$ 称为是 “$R$− 相关的”，记为 $xRy$。

等价关系

等价关系 (equivalent relations)
关系 $R ⊂ X × X$ 称为 $X$ 中的等价关系，若有：

• 自反性：$(x,x) \in R,\ \forall x \in X$
• 对称性：$(x,y) \in R \Rightarrow (y,x) \in R,\ \forall x,y \in X$
• 传递性：$(x,y) \in R\ and \ (y,z) \in R ⇒ (x,z) \in R,\ \forall x,y,z \in X$

若 $x$ 和 $y$ 之间存在等价关系，记为 $x\sim y$ 。

等价类 (equivalent class)
$x$ 所在的等价类，记为 $[x]$。它是 $X$ 的一个子集，定义为:

$[x] \equiv \{y|y ∼ x\}.$

不同的等价类之间没有交集，这些等价类的并集是 $X$。所有等价类形成的集合可以记为 $X/R$ 或 $X/\sim$。

偏序关系

偏序 (partial order)
关系 $R \subset X \times X$ 称为集合 $X$ 中的偏序，若

• 自反性：$(x,x) \in R,\ \forall x \in X$
• 反对称性：$(x,y) \in R\ and \ (y,x) \in R \Rightarrow x = y, \ \forall x,y \in X$
• 传递性：$(x,y) \in R \ and\ (y,z)\in R\Rightarrow (x,z)\in R,\ \forall x,y,z\in R$

若 $x$ 和 $y$ 由偏序 $R$ 相关，我们可以将其记为 $x \preccurlyeq y$。
有了偏序后，我们可以在某个集合中定义上限、上确界、下限、下确界、极大等概念。

全序集 (totally ordered, linear ordered)
若一个偏序集其中的任两个元素$x$ 和 $y$，要么 $x \preccurlyeq y$，要么 $y \preccurlyeq x$，则称这个偏序集为 全序集 或 线性序集。

对一堆事件点所成的集合，引入某种偏序，可以在这个集合上引入因果结构，成为因果集 (Penrose, 1950s)。在一定的假设下，这种因果结构意味着某种洛伦兹结构.

佐恩引理 (Zorn’s lemma)
对一个非空偏序集，若其任意全序子集都有上确界，则该偏序集至少具有一个极大元。