广义相对论的数学基础（三）：群、环、模

代数结构

有了集合之后，便可以考虑集合间的映射。某些集合以及与这些集合相关的映射可以给出一些特殊的结构。在泛代数中 代数结构 是在一种或多种运算下封闭的一个或多个集合。一个代数结构包含集合及符合某些公理的运算或关系。

对于集合 $X$，其上的运算分为两类：

• 内部操作 (internal operation)
  由 $X \times X$ 到 $X$ 的映射。
• 外部操作 (external operation)
  由 $A\times X$ 到 $X$ 的映射。其中 $A$ 是一个集合。

接下来，我们为一个集合添加一些运算，逐步得到群、环、域等代数结构。

群

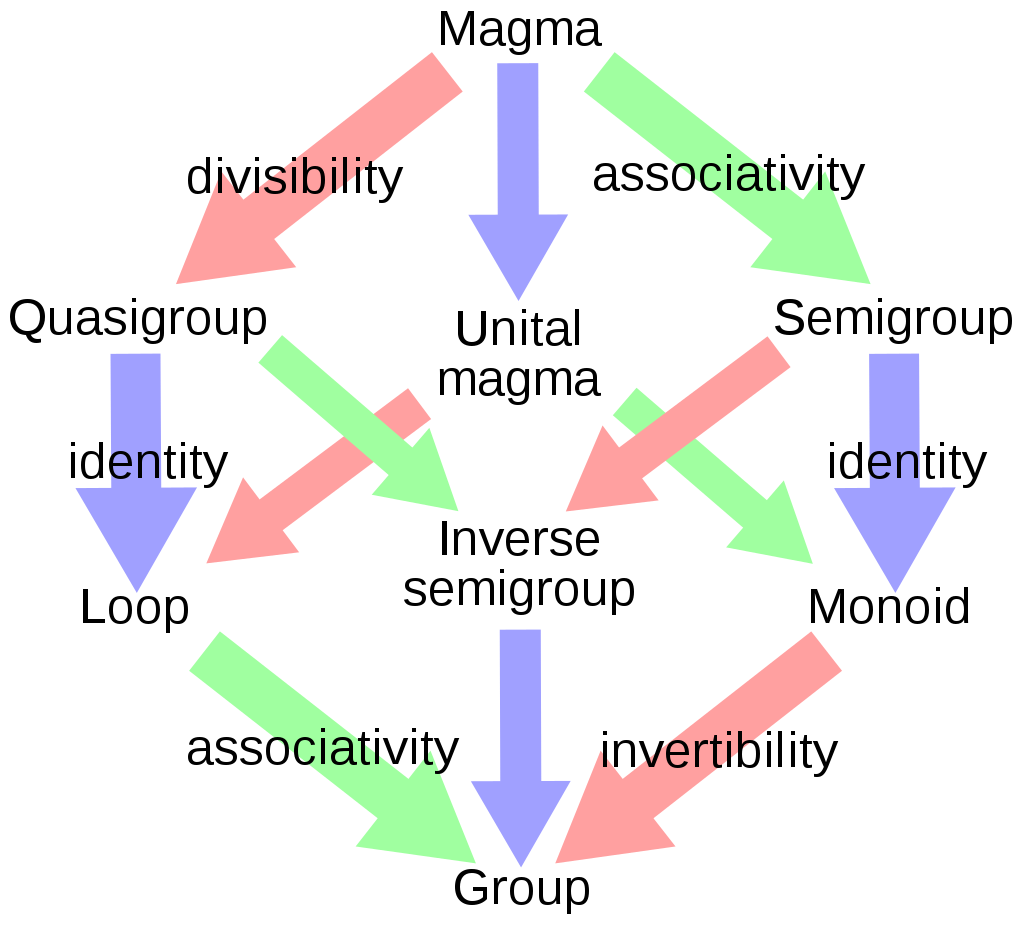
Fig1：从 Magma (一个集合与一个封闭的内部操作) 到 Group 的代数结构

半群 (semigroup)
半群是一个集合 $X$ 和其上的一个内部操作：

$X \times X \rightarrow X,\ (x,y) \mapsto xy$

并要求这个操作满足结合律

$(xy)z = x(yz),\ \forall x,y,z \in X$

用 “$\cdot$” 代表这个内部操作。这个操作也称为 乘法。

幺半群 (monoid)
幺半群是一个集合 $X$ 和其上的一个内部操作：

$X \times X \rightarrow X,\ (x,y) \mapsto xy$

并要求这个操作满足：

• 结合律

$(xy)z = x(yz),\ \forall x,y,z \in X$

• 存在恒元 $e$：

$xe = ex = x,\ \forall x \in X$

群 (group)
群是一个集合 $X$ 和其上的一个内部操作：

$X \times X \rightarrow X,\ (x,y) \mapsto xy$

并要求这个操作满足

• 结合律：

$(xy)z = x(yz),\ \forall x,y,z \in X$

• 存在恒元 $e$：

$xe = ex = x,\ \forall x \in X$

• 存在逆元：
  $\forall x \in X$，集合 $X$ 中存在一个元素，记为 $x^{−1}$，使得

$x ^{−1} x = xx^{−1} = e$

所有的群和群同态，形成一个范畴。群同态(homomorphisms) 是保持群结构的映射：

$f \in \mathrm{Hom}(G_1 ,G_2 ) \Leftrightarrow f(g_1,h_1 ) = f(g_1 )f(h_1 ),\ \forall g_1 ,h_1 \in G_1 .$

阿贝尔群 (abelian, commutative)
若 $ xy = yx,\ \forall x,y \in X$，则称这个群为阿贝尔群。这时候我们可以将群乘法写成加法的形式，即：

$xy \rightarrow x + y$

此时，恒元也可以用 “$0$” 来表示。

环

环 (ring)
环是一个集合 $X$ 和其上的两个内部操作：

$(x,y) \mapsto xy ,\ (x,y) \mapsto x + y$

这两个操作分别称为乘法和加法。并要求它们满足:

• 对于加法，$X$ 是一个阿贝尔群。
• 乘法要求满足结合律 (成半群)，且满足相对于加法的分配律：
  即 $\forall x,y,z \in X$，有：

$\begin{aligned} &(xy)z = x(yz) \\ &x(y + z) = xy + xz \\ &(y + z)x = yx + zx \\ \end{aligned}$

一些特殊的环对乘法做出进一步的要求：

• 阿贝尔环 (abelian ring)
  乘法可交换

• 幺环 (ring with identity)
  （乘法成幺半群）存在乘法恒元，即存在 $e \in X$，使得

$xe = ex = x,\ \forall x \in X$

设 $X$ 是一个幺环，元素 $x\in X$ 有逆（对于乘法），则称元素 $x$ 是 可逆的 (regular, invertible, non singular)。

对于一个幺环 $X$，若除了零（加法群的恒元）之外，其他所有元素都是可逆的，则称这个环为 域 (field)。

模

模 (module)
环 $R$ 上的模 $X$ 为一个阿贝尔群，以及一个称为标量乘积的外部操作：

$R \times X \rightarrow X,\ (\alpha,x) \mapsto \alpha x$

使得 $\forall \alpha,\beta \in R,\ x,y \in X$，有

$\begin{aligned} &\alpha (x + y) = \alpha x + \alpha y\\ &(\alpha + \beta)x = \alpha x + \beta x\\ &(\alpha\beta)x = \alpha(\beta x)\\ \end{aligned}$

（若 $R$ 有恒元，还要求标量乘积满足：$ex = x,\ \forall x \in X$）

一个模上有四个操作：

• 环 $R$ 中有两个内部操作：环的加法和乘法。
• $X$ 自身还有一个内部的操作：阿贝尔群的加法。
• 将这些内部操作联系起来的外部操作：标量乘积。

代数

结合代数
代数 (Algebra) $X$ 首先是一幺环 $R$ 上的模。其次，在 $X$ 内还要求有另一个内部操作，通常称为乘积，使得:

• $X$ 自身形成一个环
• 外部操作 $R \times X \rightarrow X,\ (\alpha,x) \mapsto \alpha x$ 满足:

$\alpha(xy) = (\alpha x)y = x(\alpha y)$

因此，一个代数上有五种操作：

• 环 $R$ 上的乘法和加法。
• 环 $X$ 上的乘法和加法。
• 将这些内部操作联系起来的外部操作：标量乘积。