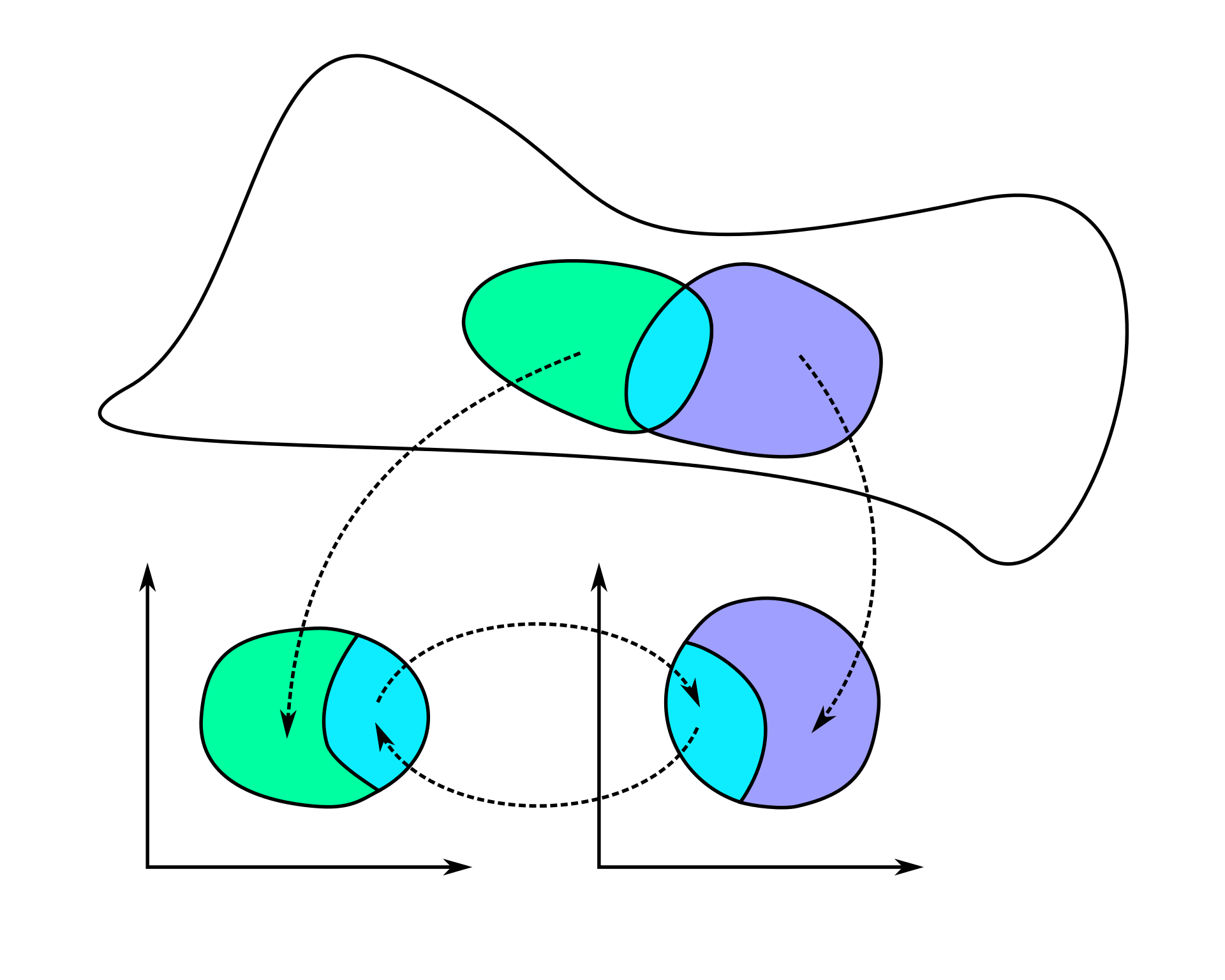
本组笔记主要为中国科学技术大学曹利明教授广义相对论与宇宙学的课程笔记。广义相对论对数学的要求比较高,我们首先从最基础开始,介绍集合与映射的概念。
集合
集合与类
集合
什么是集合?如何定义集合?实际上,严格地定义集合在数学上是一个非常复杂的问题。
简单来说,所谓的一个集合,就是将数个对象归类而分成为一个或数个形态各异的大小整体。 一般来讲,集合是具有某种特性的事物的整体,或是一些确认对象的汇集 (这只是一个描述性质的定义)。集合里的事物,叫作 元素。一个不包含任何元素的集合称为 空集 (null, empty or void set),记作:∅。
为了避免 罗素悖论,人们建立了公理化集合论,如 Zermelo 及 Fraenkel 建立的 ZF 系统,即 ZF 公理化集合论 (Zermelo-Fraenkel Set Theory)。
罗素悖论的一个通俗版本——理发师悖论:某理发师声称他给所有不给自己理发的人理发。问这位理发师给不给他自己理发?这显然会导致一个矛盾的结果。
对应到集合论中,是不是所有“具有某种特定性质的事物的总体”都能称作“集合”呢?将所有集合分为两类:P={A∣A∈A},Q={A∣A∈/Q},那么:Q∈P 还是 Q∈Q ?。
在 ZF 公理化集合论中,分类公理 通过对集合进行“限制”来避免罗素悖论。
类
在公理化集合论的研究中,人们发现数学概念 类 (classes) 比较重要。在集合论及其数学应用中:类是集合 (或其他数学物件)的搜集 (collection),可以依所有成员所共享的性质被无歧定义。
直观地说,类是一个比集合更普遍、更大的概念。
例如:所有可能的具备一定代数结构的对象 (群、环、模等)都形成一个类,但不是一个集合。一个不是集合的类被称为 真类 (proper class) ,一个是集合的类被称为“小类”。
集合的关系与运算
集合间的关系
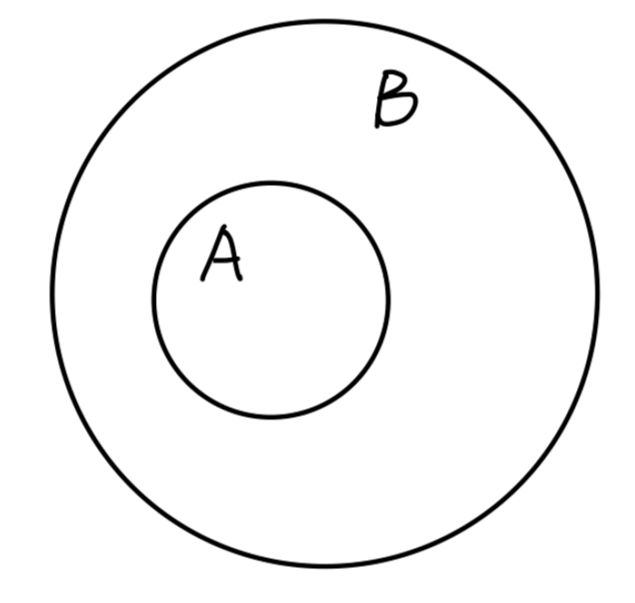
Fig: A 是 B 的子集
对于集合 A,B,若满足:
∀ a∈A, s.t. a∈B
则称 A 是 B 的 子集,记作:
A⊂B
读作:A ** (包)含于** B,B 包含 A。若 A⊂B 且 $ A\neq B$,则称 A 为 B 的 真子集,记作:
A⊊B
读作:A 真 (包)含于 B,B 真包含 A。
包含关系 ⊂ 是集合间的一个 非严格偏序关系,真包含关系 ⊊ 是集合间的一个 严格偏序关系 (在之后的“关系”中会阐述)。
集合的运算
A∪B≡{x∣x∈A or x∈B}
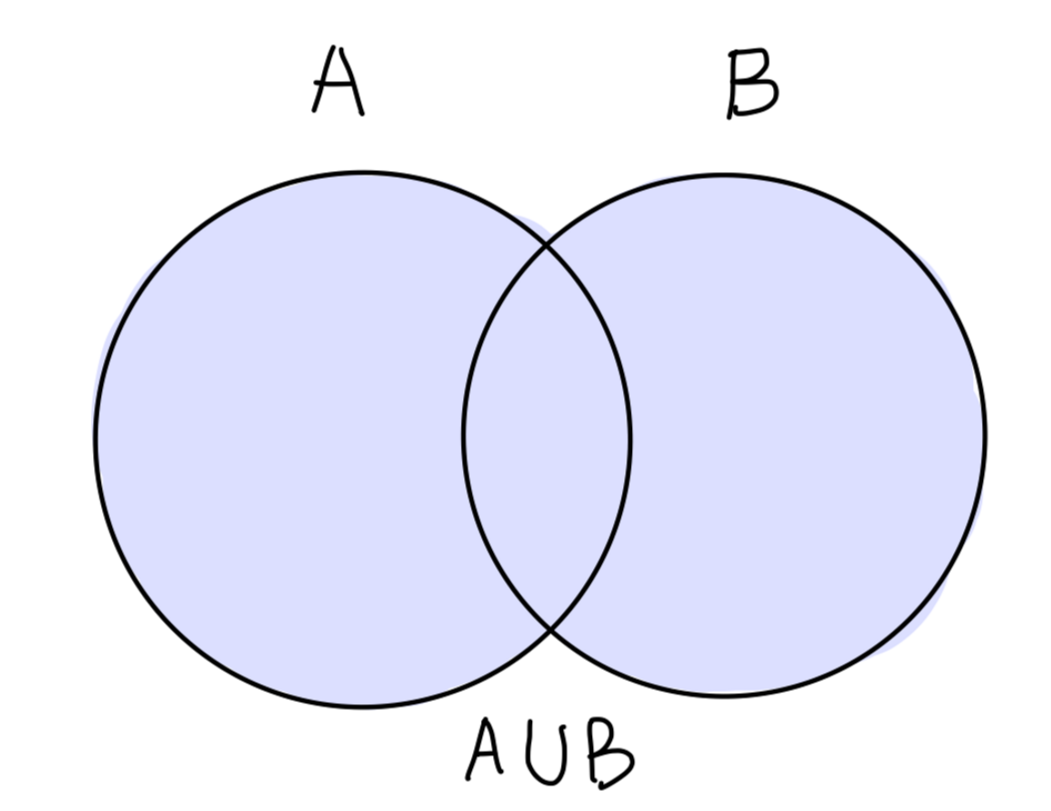
Fig:A 和 B 的并集
A∩B≡{x∣x∈A and x∈B}

Fig:A 和 B 的交集
若 A∩B=∅,称 A,B 无交集 (disjoint)。
- 补集 (complement)
若 A⊂U,A 关于全集 U 的补集为:
∁UA≡{x∣x∈/A and x∈U}
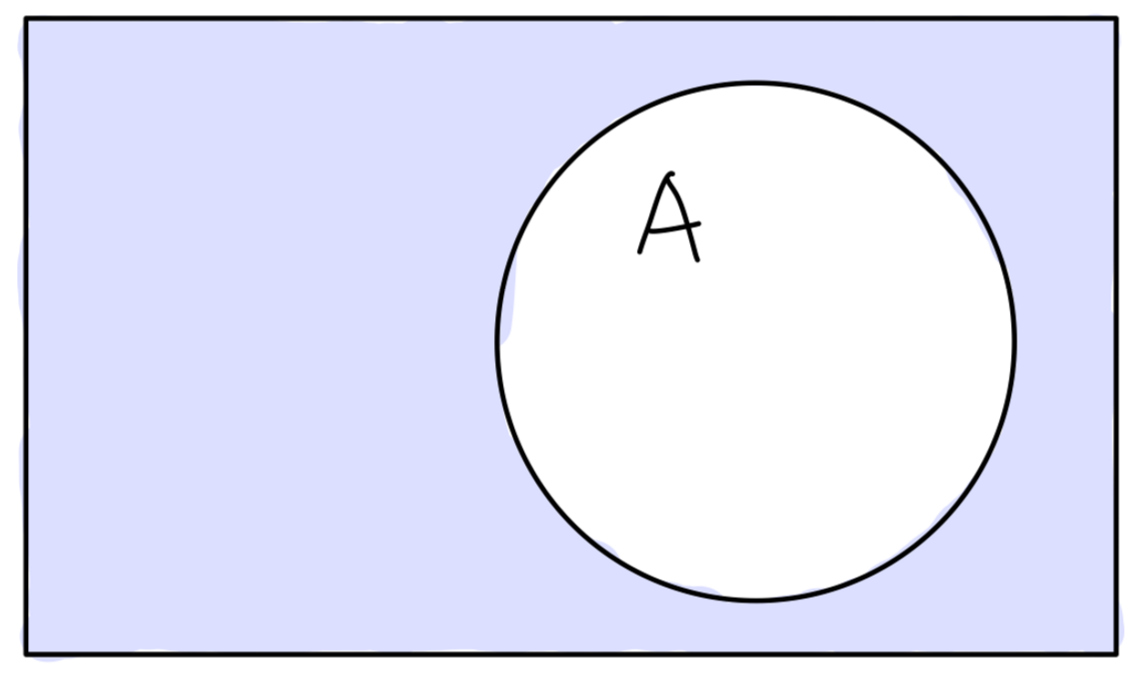
Fig:A 关于全集 U 的补集
- 差集 (difference):
两个集合也可以相"减"。A 在 B 中的 相对补集 (差集) 定义为:
A∖B≡{x∣x∈A and x∈/B}
若 A⊂U,B⊂U,则有:
A∖B=A∩∁UB
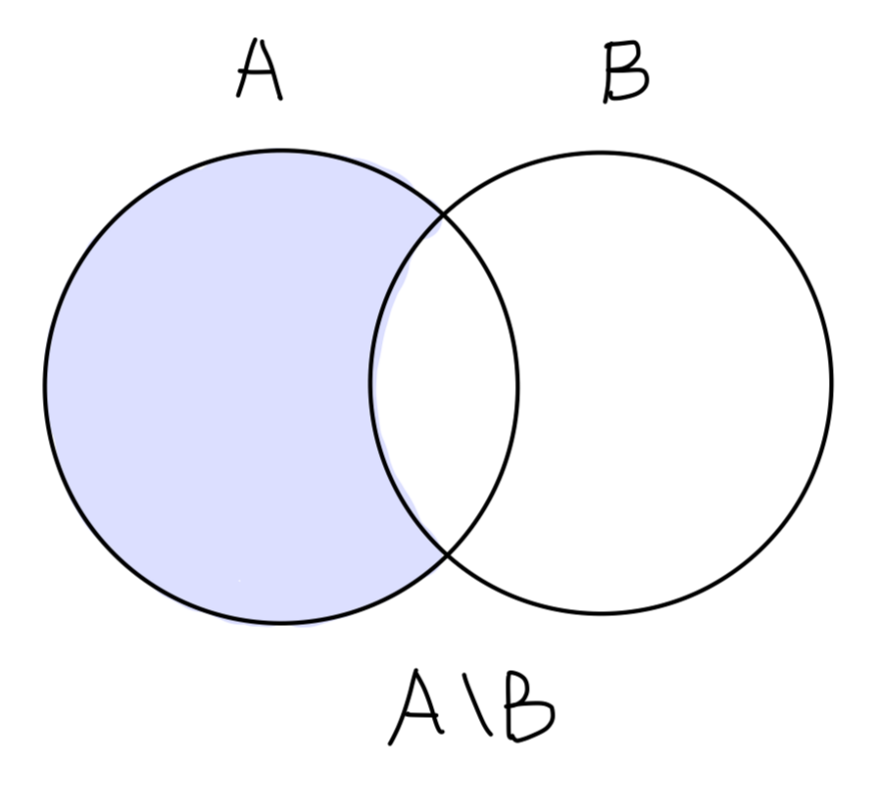
Fig:相对补集 A∖B
利用差集,则对于补集,有:
∁UA=U∖A
- 对称差集 (symmetric difference)
若 A⊂U,B⊂U,则其对称差运算如下:
A△B≡(A−B)∪(B−A)
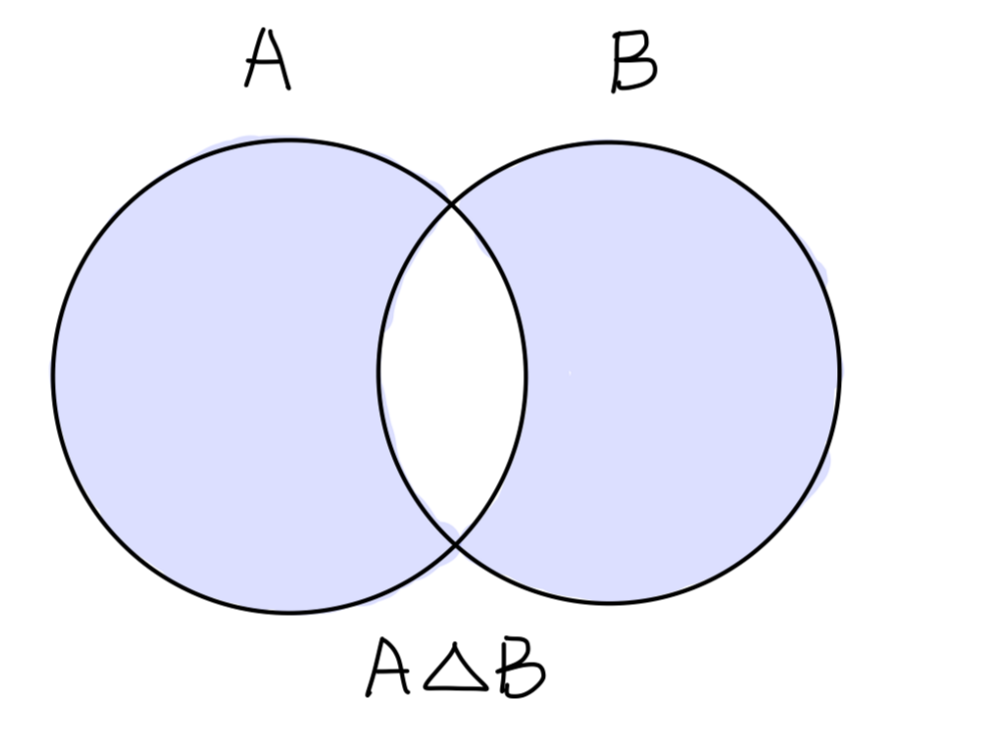
Fig:对称差集 A△B
- 集合的 卡氏积 (直积) (Cartisian product):
X×Y≡{(x,y)∣x∈X,y∈Y}
- 幂集 (power set)
X 的幂集为其所有子集的集合,记为 2X:
2X≡{A∣A⊂X}
对于交并补运算,它们具有如下基本性质,可以利用它们简化集合间的运算:
X∪Y=Y∪X,X∩Y=Y∩X
(X∪Y)∪Z=X∪(Y∪Z)(X∩Y)∩Z=X∩(Y∩Z)
(X∩Y)∪Z=(X∪Z)∩(Y∪Z)(X∪Y)∩Z=(X∩Z)∪(Y∩Z)
X∖(Y∪Z)=(X∖Y)∩(X∖Z)X∖(Y∩Z)=(X∖Y)∪(X∖Z)
若 Y,Z⊂X:
∁X∖(Y∪Z)=(∁X∖Y)∩(∁X∖Z)∁X∖(Y∩Z)=(∁X∖Y)∪(∁X∖Z)
有关 De Morgan 律,我们不妨尝试对第一式给出一个证明:
⇔⇔⇔⇔⇔∀x(x∈X∖(Y∪Z))∀x((x∈X)∧(x∈/Y∪Z))∀x((x∈X)∧((x∈/Y)∧(x∈/Z)))∀x(((x∈X)∧(x∈/Y))∧((x∈X)∧(x∈/Z))))∀x((x∈X∖Y)∧(x∈X∖Z))∀x(x∈(X∖Y)∩(X∖Z))
即得到:
∀x((x∈X∖(Y∪Z))⇔(x∈(X∖Y)∩(X∖Z)))
因此有:
X∖(Y∪Z)=(X∖Y)∩(X∖Z)
映射
映射的基本概念
映射 (mapping)
设 A 和 B 是两个非空集合,若对 A 中的任一元素 x,依照某种规律 (或法则)f,恒有 B 中的唯一确定的元素 y 与之对应,则称对应规律 f 为一个从 A 到 B 的 映射$。记作:
f:A→B
若侧重于表示为 A 中元素 x 到 B 中元素 y 的映射,常记作:
f:x↦y
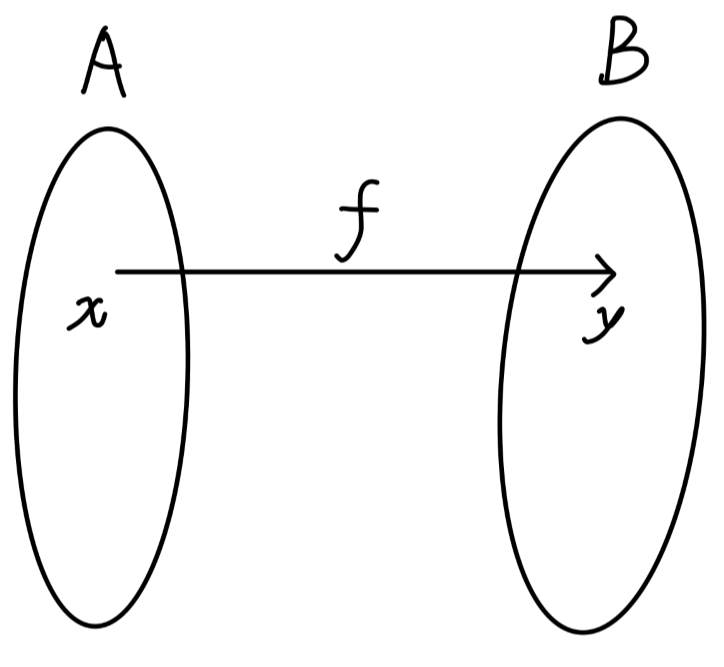
上述定义中。称 y 为 x 的 像(image),记作 y=f(x);称 x 为 y 的 原像;集合 A 为映射 f 的 定义域 (domain),记作 D(f)=A;集合 B 称为 f 的 培域 (codomain);集合 Rf={f(x)∣x∈A} 称为f 的 值域(range),或称为 A 在 f 作用下的 像。对 B 的某一子集 Y,集合 {x∣f(x)∈B} 称为 Y 的 逆像(inverse image)。
单射、满射与双射
我们根据定义域和陪域的关联方式将映射分为三类。
-
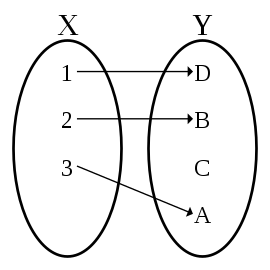
单射 (one-to-one mapping, injection)
对每一个 y∈f(X),存在一个唯一的 x∈X 使得 f(x)=y。
-
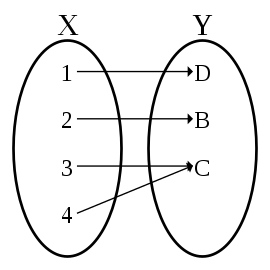
满射 (onto mapping, surgection)
对任意一个 y∈Y 都有逆。
-
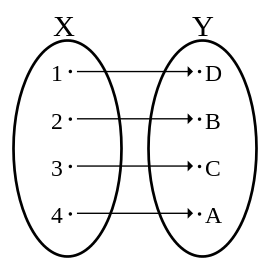
双射 (bijection)
既是单射又是满射。
映射的其他概念
- 复合映射 (composite mappings):
设 f 和 g 是两个映射:
f:X→Y, g:Y→Z
则称 g∘f:X→Z,x↦g(f(x)) 为 f 和 g 的复合映射。
- 映射的限制 (restriction)
映射 f 在某个子集 U 上的限制记为 f∣U,对应法则不变而定义域发生了变化。即:
f∣U:U→Y, x↦f(x)
- 映射的扩张 (extension)
映射 f 称为映射 g 的扩张,若:
D(f)⊃D(g),且对于任意 x∈D(g),有 f(x)=g(x)。
反过来有:
g=f∣U(g)
-
常映射 (constant mapping)
映射 f 称为常映射,若:
∀x,x′∈D(f),有 f(x)=f(x′)。
-
恒等映射 (identity mapping)
映射 f:X→X, x↦x 称为恒等映射. 通常记为 Id。它显然是个双射。即:
IdX:X→X,x↦x
- 子集的 序列 (sequence)
集合 X 的一些子集 {An} 称为一个序列,若由它可构造一个映射
N↦2X,n↦An
就是将其子集按照一定顺序排列