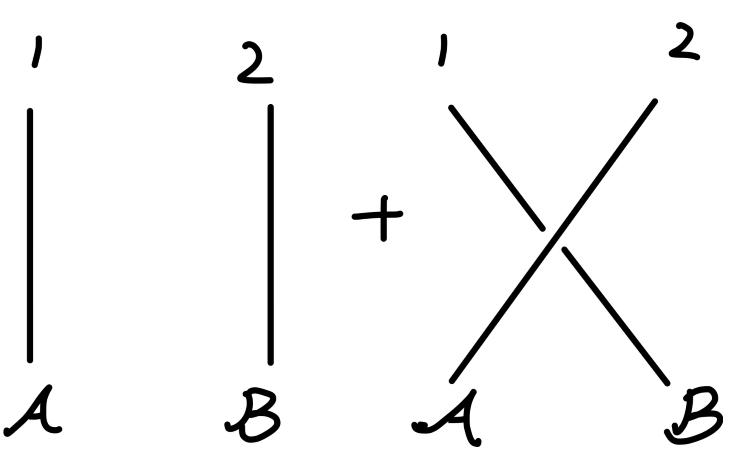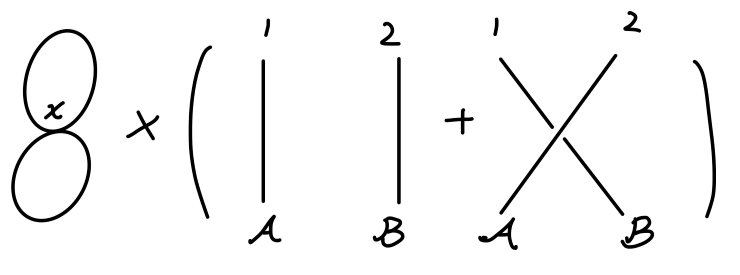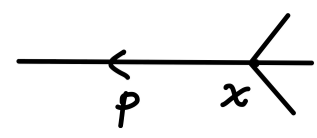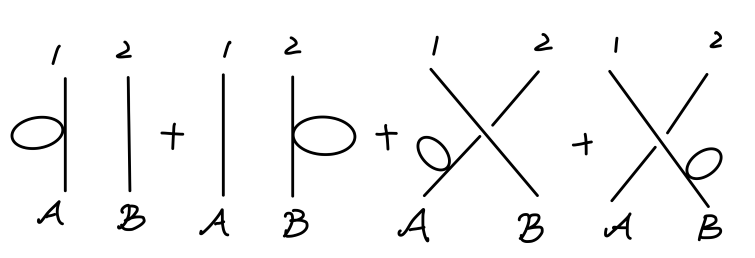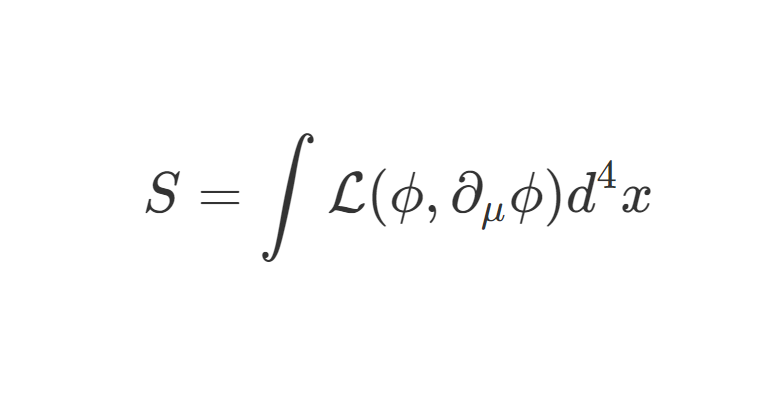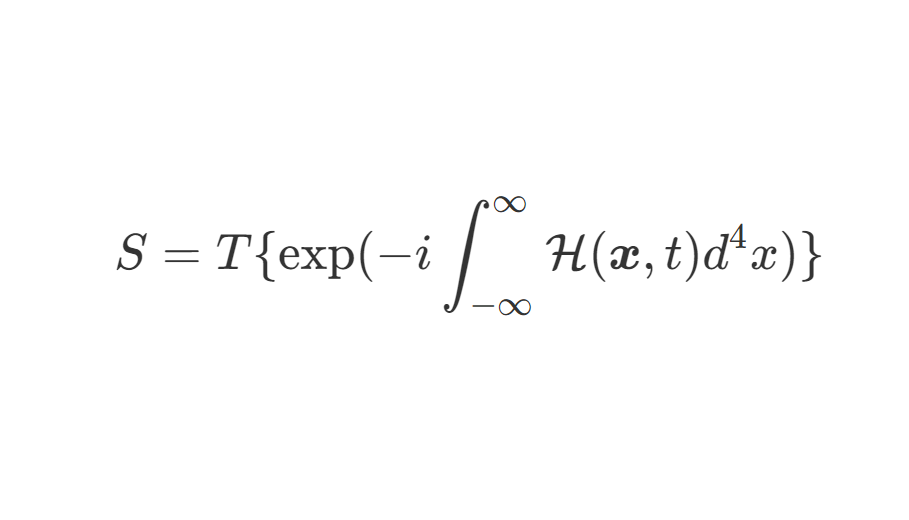现在尝试用费曼图进行散射矩阵的计算。考虑散射过程:A , B → 1 , ⋯ , n \mathcal{A},\mathcal{B}\rightarrow 1,\cdots,n A , B → 1 , ⋯ , n
⟨ p 1 ⋯ p n ∣ S ∣ p A p B ⟩ = ⟨ p 1 ⋯ p n ∣ T { exp [ − i ∫ − ∞ ∞ d t H I ( t ) ] } ∣ p A p B ⟩ (1) \langle \bm{p}_1\cdots \bm{p}_n|S|\bm{p}_{\mathcal{A}}\bm{p}_{\mathcal{B}}\rangle = \langle \bm{p}_1\cdots \bm{p}_n|T\{\exp[-i\int_{-\infty}^{\infty}dtH_I(t)]\}|\bm{p}_{\mathcal{A}}\bm{p}_{\mathcal{B}}\rangle \tag{1}
⟨ p 1 ⋯ p n ∣ S ∣ p A p B ⟩ = ⟨ p 1 ⋯ p n ∣ T { exp [ − i ∫ − ∞ ∞ d t H I ( t ) ] } ∣ p A p B ⟩ ( 1 )
最简单情况,考虑末态仅有两粒子(考虑均为 Klein-Gordon 玻色子的情形,对于不同粒子、自旋不为零的情形,我们只需要引入更多的 δ \delta δ
⟨ p 1 p 2 ∣ T { exp [ − i ∫ − ∞ ∞ d t H I ( t ) ] } ∣ p A p B ⟩ (2) \langle \bm{p}_1\bm{p}_2|T\{\exp[-i\int_{-\infty}^{\infty}dtH_I(t)]\}|\bm{p}_{\mathcal{A}}\bm{p}_{\mathcal{B}}\rangle \tag{2}
⟨ p 1 p 2 ∣ T { exp [ − i ∫ − ∞ ∞ d t H I ( t ) ] } ∣ p A p B ⟩ ( 2 )
零阶项为:
⟨ p 1 p 2 ∣ p A p B ⟩ = 2 E 1 2 E 2 2 E A 2 E B ⟨ 0 ∣ a ^ p 1 a ^ p 2 a ^ p A † a ^ p B † ∣ 0 ⟩ = 2 E A 2 E B ( δ ( 3 ) ( p A − p 1 ) δ ( 3 ) ( p B − p 2 ) + δ ( 3 ) ( p A − p 2 ) δ ( 3 ) ( p B − p 1 ) ) \begin{aligned}
\langle \bm{p}_1\bm{p}_2|\bm{p}_{\mathcal{A}}\bm{p}_{\mathcal{B}}\rangle &= \sqrt{2E_12E_22E_{\mathcal{A}}2E_{\mathcal{B}}}\langle 0| \hat{a}_{\bm{p}_1}\hat{a}_{\bm{p}_2}\hat{a}^\dagger_{\bm{p}_{\mathcal{A}}}\hat{a}^\dagger_{\bm{p}_{\mathcal{B}}}|0\rangle \\
&= 2E_{\mathcal{A}}2E_{\mathcal{B}}(\delta^{(3)}(\bm{p}_{\mathcal{A}}-\bm{p}_1)\delta^{(3)}(\bm{p}_{\mathcal{B}}-\bm{p}_2) + \delta^{(3)}(\bm{p}_{\mathcal{A}}-\bm{p}_2)\delta^{(3)}(\bm{p}_{\mathcal{B}}-\bm{p}_1))
\end{aligned}
⟨ p 1 p 2 ∣ p A p B ⟩ = 2 E 1 2 E 2 2 E A 2 E B ⟨ 0 ∣ a ^ p 1 a ^ p 2 a ^ p A † a ^ p B † ∣ 0 ⟩ = 2 E A 2 E B ( δ ( 3 ) ( p A − p 1 ) δ ( 3 ) ( p B − p 2 ) + δ ( 3 ) ( p A − p 2 ) δ ( 3 ) ( p B − p 1 ) )
其中的 δ \delta δ δ ( α − β ) \delta(\alpha-\beta) δ ( α − β )
S = 1 + i T (3) S = 1 + iT \tag{3}
S = 1 + i T ( 3 )
我们更关心相互作用的带来的影响,这体现在 i T iT i T
一阶项为:
⟨ p 1 p 2 ∣ T { − i ∫ d t H I ( t ) } ∣ p A p B ⟩ (4) \langle \bm{p}_1\bm{p}_2|T\{-i\int dtH_I(t)\} |\bm{p}_{\mathcal{A}}\bm{p}_{\mathcal{B}}\rangle \tag{4}
⟨ p 1 p 2 ∣ T { − i ∫ d t H I ( t ) } ∣ p A p B ⟩ ( 4 )
对于 ϕ 4 \phi^4 ϕ 4
⟨ p 1 p 2 ∣ T { − i ∫ d 4 z ϕ 4 ( z ) } ∣ p A p B ⟩ = ⟨ p 1 p 2 ∣ N { − i ∫ d 4 z ϕ 4 ( z ) + c o n t r a c t i o n s } ∣ p A p B ⟩ (5) \begin{aligned}
&\langle \bm{p}_1\bm{p}_2|T\{-i\int d^4z \phi^4(z)\} |\bm{p}_{\mathcal{A}}\bm{p}_{\mathcal{B}}\rangle\\
=& \langle \bm{p}_1\bm{p}_2|N\{-i\int d^4z \phi^4(z) + contractions\} |\bm{p}_{\mathcal{A}}\bm{p}_{\mathcal{B}}\rangle\\
\end{aligned}\tag{5}
= ⟨ p 1 p 2 ∣ T { − i ∫ d 4 z ϕ 4 ( z ) } ∣ p A p B ⟩ ⟨ p 1 p 2 ∣ N { − i ∫ d 4 z ϕ 4 ( z ) + c o n t r a c t i o n s } ∣ p A p B ⟩ ( 5 )
第二步应用了 wick 定理,不同的是:现在并非是只有场量完全缩并的项才对散射矩阵有贡献。我们可以将零阶项的计算看做是初态与末态的缩并:
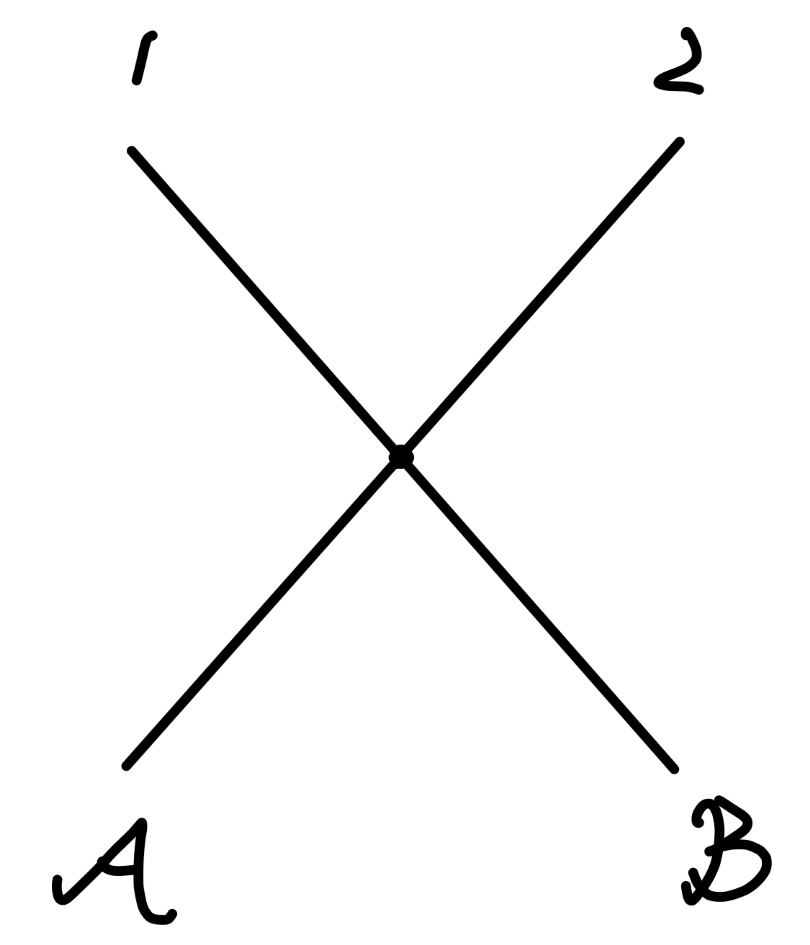
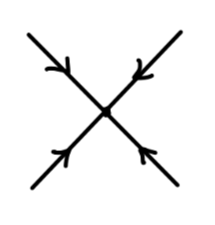
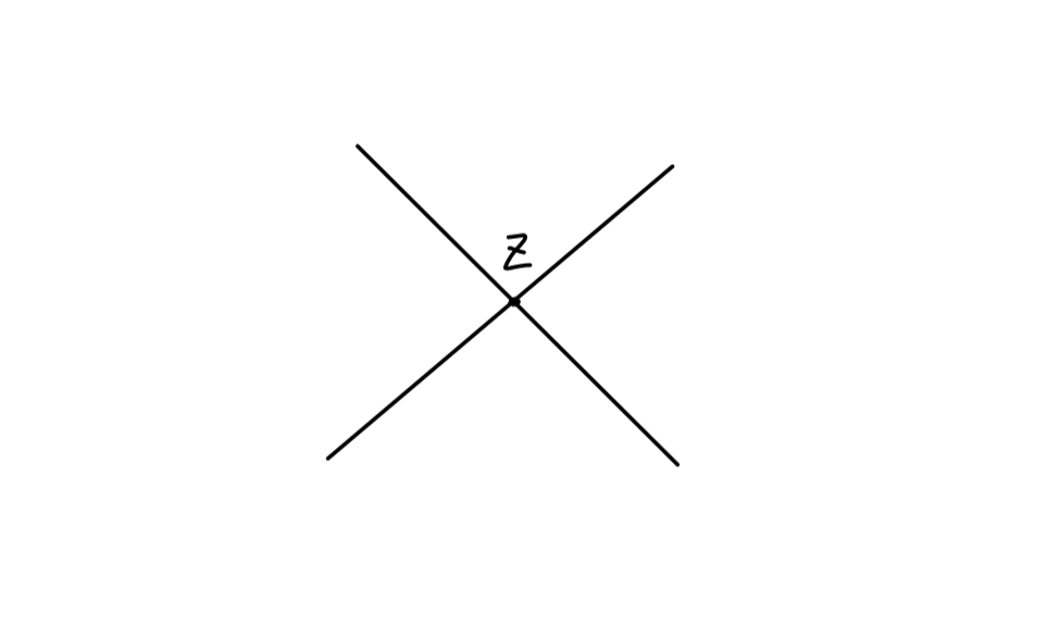
⟨ p 1 p 2 ∣ p A p B ⟩ = ⟨ p 1 ∙ p 2 ⋆ ∣ p A ∙ p B ⋆ ⟩ + ⟨ p 1 ∙ p 2 ⋆ ∣ p A ⋆ p B ∙ ⟩ \begin{aligned}
\langle \bm{p}_1\bm{p}_2|\bm{p}_{\mathcal{A}}\bm{p}_{\mathcal{B}}\rangle = \langle \bm{p}^{\bullet}_1\bm{p}^{\star}_2|\bm{p}^{\bullet}_{\mathcal{A}}\bm{p}^{\star}_{\mathcal{B}}\rangle + \langle \bm{p}^{\bullet}_1\bm{p}^{\star}_2|\bm{p}^{\star}_{\mathcal{A}}\bm{p}^{\bullet}_{\mathcal{B}}\rangle
\end{aligned}
⟨ p 1 p 2 ∣ p A p B ⟩ = ⟨ p 1 ∙ p 2 ⋆ ∣ p A ∙ p B ⋆ ⟩ + ⟨ p 1 ∙ p 2 ⋆ ∣ p A ⋆ p B ∙ ⟩
用费曼图表示为:
Fig1:散射矩阵零阶项
类似的,我们可以也可以考虑场量与初态/末态的缩并。通过计算:
ϕ I + ( x ) ∣ p ⟩ = ∫ d 3 k ( 2 π ) 3 1 2 E k a ^ k e − i k ⋅ x 2 E p a ^ p † ∣ 0 ⟩ = ∫ d 3 k 1 2 E k e − i k ⋅ x 2 E p δ ( k − p ) ∣ 0 ⟩ = e − i p ⋅ x ∣ 0 ⟩ (6) \begin{aligned}
\phi^{+}_I(x)|\bm{p}\rangle &= \int \frac{d^3k}{(2\pi)^3} \frac{1}{\sqrt{2E_{\bm{k}}}} \hat{a}_{\bm{k}}e^{-ik\cdot x} \sqrt{2E_{\bm{p}}} \hat{a}_{\bm{p}}^\dagger |0\rangle\\
&= \int d^3k \frac{1}{\sqrt{2E_{\bm{k}}}} e^{-ik\cdot x} \sqrt{2E_{\bm{p}}} \delta(\bm{k}-\bm{p}) |0\rangle\\
&= e^{-ip\cdot x} |0\rangle\\
\end{aligned}\tag{6}
ϕ I + ( x ) ∣ p ⟩ = ∫ ( 2 π ) 3 d 3 k 2 E k 1 a ^ k e − i k ⋅ x 2 E p a ^ p † ∣ 0 ⟩ = ∫ d 3 k 2 E k 1 e − i k ⋅ x 2 E p δ ( k − p ) ∣ 0 ⟩ = e − i p ⋅ x ∣ 0 ⟩ ( 6 )
同理,ϕ I − ( x ) \phi_{I}^-(x) ϕ I − ( x )
⟨ p ∣ ϕ I − ( x ) = ⟨ 0 ∣ e i p ⋅ x (7) \langle \bm{p}|\phi^{-}_I(x) = \langle 0|e^{ip\cdot x} \tag{7}
⟨ p ∣ ϕ I − ( x ) = ⟨ 0 ∣ e i p ⋅ x ( 7 )
那么我们定义场量与入射态/出射态的缩并为:
ϕ I ∙ ( x ) ∣ p ∙ ⟩ = e − i p ⋅ x ∣ 0 ⟩ ⟨ p ∙ ∣ ϕ I ∙ ( x ) = ⟨ 0 ∣ e i p ⋅ x (8) \begin{aligned}
\phi^{\bullet}_I(x)|\bm{p}^{\bullet}\rangle &= e^{-ip\cdot x} |0\rangle\\
\langle \bm{p}^{\bullet}|\phi^{\bullet}_I(x) &= \langle 0|e^{ip\cdot x}\\
\end{aligned}\tag{8}
ϕ I ∙ ( x ) ∣ p ∙ ⟩ ⟨ p ∙ ∣ ϕ I ∙ ( x ) = e − i p ⋅ x ∣ 0 ⟩ = ⟨ 0 ∣ e i p ⋅ x ( 8 )
因此在 ( 5 ) (5) ( 5 )
那么考虑到 ( 5 ) (5) ( 5 )
ϕ ϕ ϕ ϕ ; ϕ ∙ ϕ ∙ ϕ ϕ ; ϕ ∙ ϕ ∙ ϕ ∙ ∙ ϕ ∙ ∙ ; \phi\phi\phi\phi;\quad \phi^{\bullet}\phi^{\bullet}\phi\phi;\quad \phi^{\bullet}\phi^{\bullet}\phi^{\bullet\bullet}\phi^{\bullet\bullet};
ϕ ϕ ϕ ϕ ; ϕ ∙ ϕ ∙ ϕ ϕ ; ϕ ∙ ϕ ∙ ϕ ∙ ∙ ϕ ∙ ∙ ;
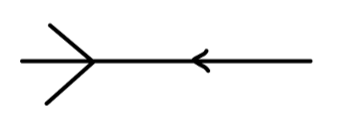
第三种类型 :场量完全缩并,可以用如下费曼图表示:
Fig2:散射矩阵一阶项:类型3
它仍然保证初态等于末态,因此不对 T T T
第二种类型 :需要考虑场量与初态\末态之间的缩并。
我们给出场量与初态\末态之间的缩并的费曼图:
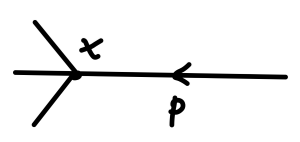
ϕ I ∙ ( x ) ∣ p ∙ ⟩ \phi_I^{\bullet}(x)|\bm{p}^{\bullet}\rangle ϕ I ∙ ( x ) ∣ p ∙ ⟩
Fig3:场量与末态缩并
⟨ p ∙ ∣ ϕ I ∙ ( x ) \langle \bm{p}^\bullet|\phi_I^{\bullet}(x) ⟨ p ∙ ∣ ϕ I ∙ ( x )
Fig4:场量与初态缩并
初态/末态对应的元素为 外部线 external line 。一般来说,我们通常规定费曼图从左到右为时间增加的方向,因此可以根据时间顺序区分初态/末态。
对应的费曼图为:
Fig5:散射矩阵一阶项:类型2
由于顶点保证四动量守恒,因此初态与末态也是一样的,这些图不对 T T T
第一种类型 :没有场量间的缩并,只有场量与初态/末态的缩并。
其费曼图为:
Fig6:散射矩阵一阶项:类型1
其值为:
( 4 ! ) ⋅ ( − i λ 4 ! ) ∫ d 4 x e − i ( p A + p B − p 1 − p 2 ) ⋅ x = − i λ ( 2 π ) 4 δ ( 4 ) ( p A + p B − p 1 − p 2 ) \begin{aligned}
&(4!)\cdot(-i\frac{\lambda}{4!})\int d^4x e^{-i(p_{\mathcal{A}}+p_{\mathcal{B}}-p_1-p_2)\cdot x}\\
=& -i\lambda (2\pi)^4 \delta^{(4)}(p_{\mathcal{A}}+p_{\mathcal{B}}-p_1-p_2)
\end{aligned}
= ( 4 ! ) ⋅ ( − i 4 ! λ ) ∫ d 4 x e − i ( p A + p B − p 1 − p 2 ) ⋅ x − i λ ( 2 π ) 4 δ ( 4 ) ( p A + p B − p 1 − p 2 )
其中 4 ! 4! 4 !
它对 T T T
那么我们现在可以得到:只有那些 完全连通 fully connected (四个外部线彼此相连)的图才对 T T T
现在我们要问,考虑到所有的高阶项之后,是否 T T T
⟨ p 1 p 2 ∣ i T ∣ p A p B ⟩ \langle \bm{p}_1 \bm{p}_2|iT|\bm{p}_{\mathcal{A}}\bm{p}_{\mathcal{B}}\rangle
⟨ p 1 p 2 ∣ i T ∣ p A p B ⟩
等于那些 具有完全连通部分的费曼图的总和 ?
用费曼图表示为:
Fig:散射矩阵
我们根据图的特点将这些图分为三类,分别写到三行。第一类图有贡献是容易理解的。而根据对关联函数的讨论,第一第二类图的总贡献等价于乘以一个因子:
exp ( ∑ i V i ) \exp(\sum_{i} V_i)
exp ( i ∑ V i )
其中 V i V_i V i
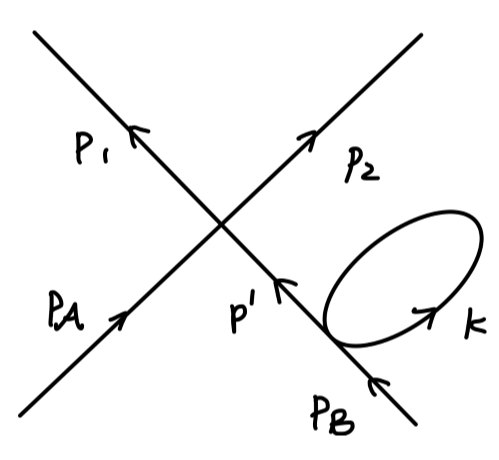
对于第三类图,我们不妨以其中一个图为例作以下计算:
其值为:
1 2 ∫ d 4 p ′ ( 2 π ) 4 i p ′ 2 − m 2 ∫ i k 2 − m 2 × ( − i λ ) ( 2 π ) 4 δ ( 4 ) ( p A + p ′ − p 1 − p 2 ) × ( − i λ ) ( 2 π ) 4 δ ( 4 ) ( p B − p ′ ) \begin{aligned}
&\frac{1}{2}\int \frac{d^4p'}{(2\pi)^4} \frac{i}{p'^2 - m^2} \int \frac{i}{k^2-m^2}\\
&\times(-i\lambda)(2\pi)^4\delta^{(4)}(p_\mathcal{A} + p' - p_1 -p_2)\\
&\times (-i\lambda)(2\pi)^4\delta^{(4)}(p_\mathcal{B} - p')\\
\end{aligned}
2 1 ∫ ( 2 π ) 4 d 4 p ′ p ′ 2 − m 2 i ∫ k 2 − m 2 i × ( − i λ ) ( 2 π ) 4 δ ( 4 ) ( p A + p ′ − p 1 − p 2 ) × ( − i λ ) ( 2 π ) 4 δ ( 4 ) ( p B − p ′ )
利用第 2 2 2 δ \delta δ p ′ p' p ′
i p ′ 2 − m 2 ∣ p ′ = p B = i p B 2 − m 2 = i 0 \frac{i}{p'^2-m^2}|_{p' = p_{\mathcal{B}}} = \frac{i}{p_{\mathcal{B}}^2 - m^2} = \frac{i}{0}
p ′ 2 − m 2 i ∣ p ′ = p B = p B 2 − m 2 i = 0 i
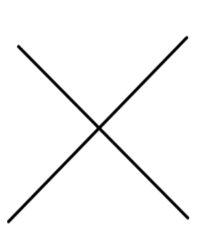
这会导致发散!现在我们不能想象费曼图发散这件事情。更糟糕的,对于任意一个看起来很好的费曼图,例如:
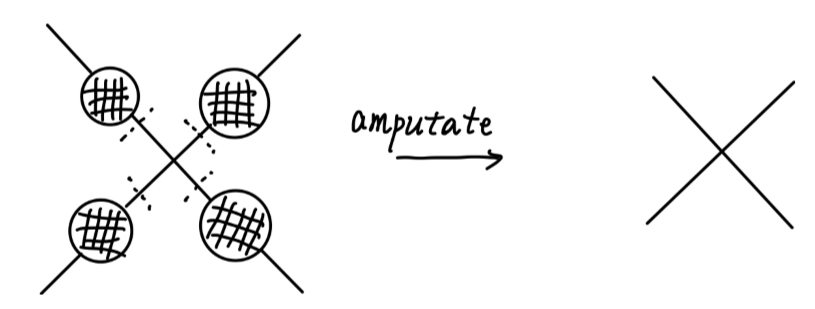
我们都可以在上添加一个 bubble 使得它的性质变差。
我们称前一个图为 amputated diagram 。一般的图可以表示为,通过 amputation ,可以得到对应的 amputated diagram 。
例如:
左图中的黑色 bubble 表示所有可能的连通费曼图。
那么如何解决无穷大的问题呢?
我们先想:对于一个费曼图:哪些量是可以被观测的,而那些并不是可观测量?
那些初态与末态是我们观测到的,而中间发生的过程我们其实并没有观测到。所有我们观测到的物理量:例如电荷、质量等,并没有出现无穷大的情况。而这些发散的图显然也对电荷、质量的测量有贡献,这必然说明在拉格朗日量中出现的电荷、质量、耦合常数等参数只能是 裸参数 bare parameters ,并不对应测量得到的物理量。
如何确定这些裸参数?通过引入能量截断,可以使得那些本来发散的费曼图的值成为一个依赖于截断的量,我们再根据计算的精度,将需要考虑的费曼图进行求和,这也是依赖于截断的,再令此时的测量值正好等于真实的物理量,就能得到那些依赖于截断的裸参数。这就是 重整化 Renormalization 的方法。我们将在以后进行详细讨论。
那么现在,我们只要将裸参数换成对应的真实物理量,就只需要考虑那些 amputated diagram 的贡献了。
于是得到:
⟨ p 1 p 2 ∣ i T ∣ p A p B ⟩ = ∑ { f u l l y c o n n e c t e d a m p u t a t e d d i a g r a m } (9) \langle \bm{p}_1 \bm{p}_2|iT|\bm{p}_{\mathcal{A}}\bm{p}_{\mathcal{B}}\rangle = \sum \left\{ \begin{aligned}
&fully\ connected\ \\
&utated\ diagram\ \\
\end{aligned}\right\} \tag{9}
⟨ p 1 p 2 ∣ i T ∣ p A p B ⟩ = ∑ { f u l l y c o n n e c t e d a m p u t a t e d d i a g r a m } ( 9 )
根据以上的讨论,我们总结坐标空间的费曼规则:
值为:
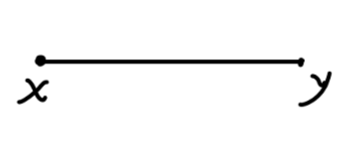
D F ( x − y ) D_F(x-y)
D F ( x − y )
值为:
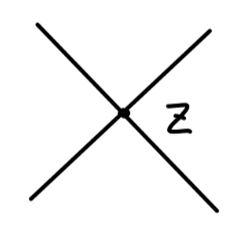
( − i λ ) ∫ d 4 z (-i\lambda) \int d^4z
( − i λ ) ∫ d 4 z
值为:
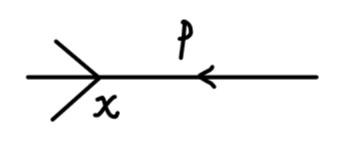
e − i p ⋅ x e^{-ip\cdot x}
e − i p ⋅ x
类似的,我们容易得到动量空间中的费曼规则:
值为:
i p 2 − m 2 + i ϵ \frac{i}{p^2 - m^2 + i\epsilon}
p 2 − m 2 + i ϵ i
值为:
− i λ -i\lambda
− i λ
值为:
1 1
1
∫ d 4 p ( 2 π ) 4 \int \frac{d^4p}{(2\pi)^4}
∫ ( 2 π ) 4 d 4 p