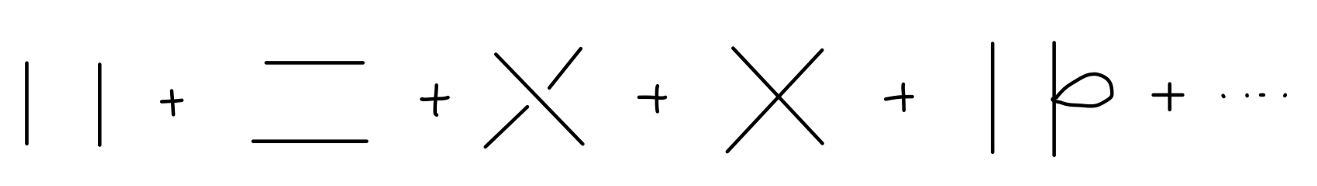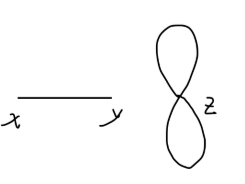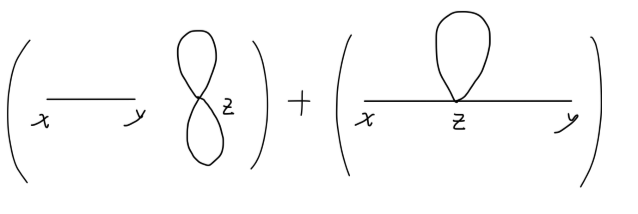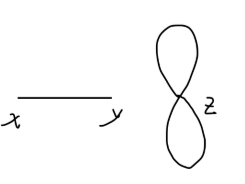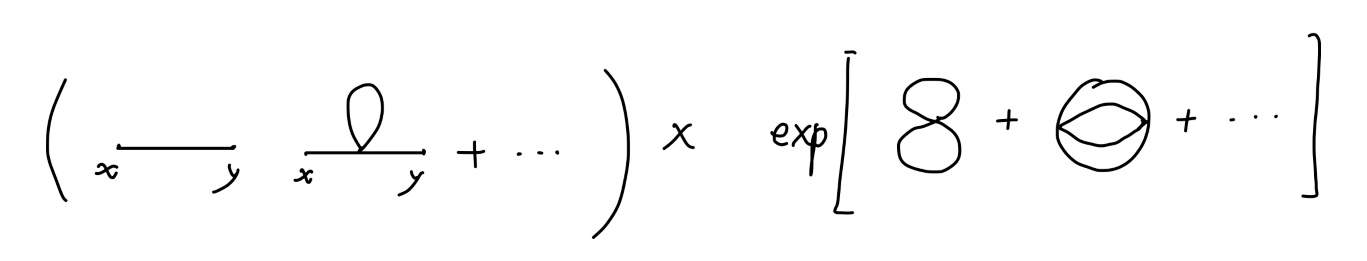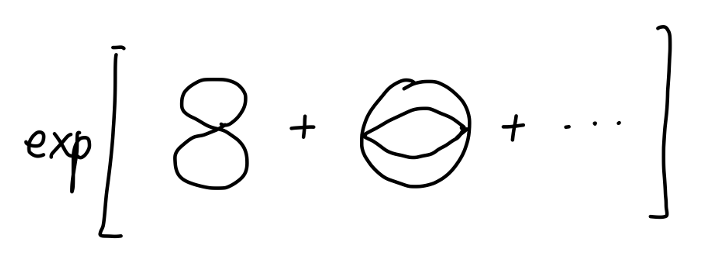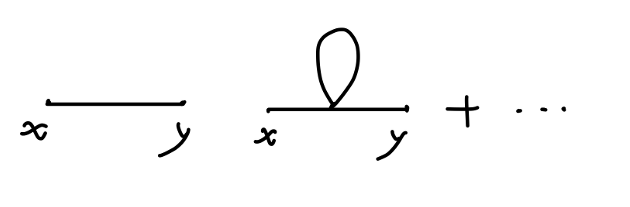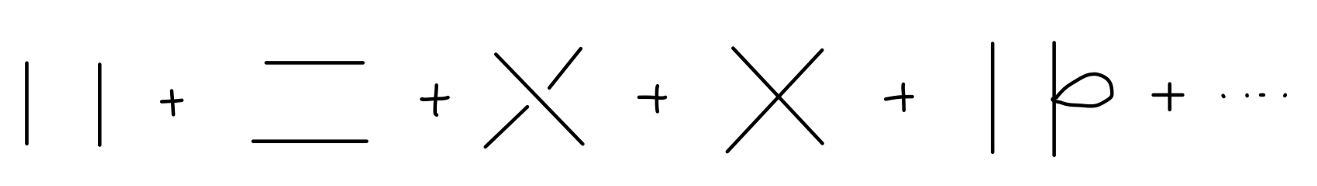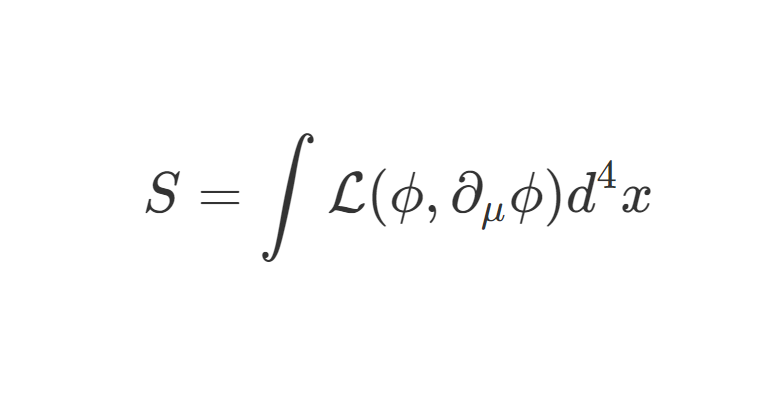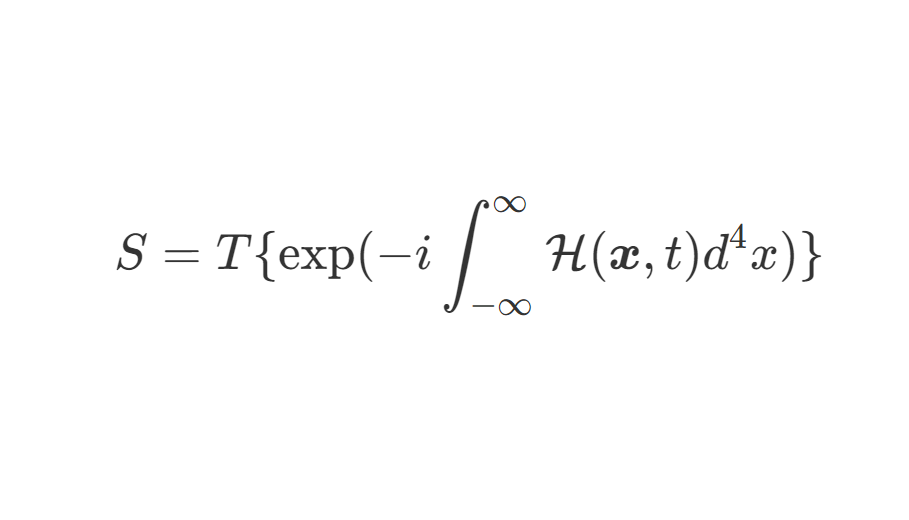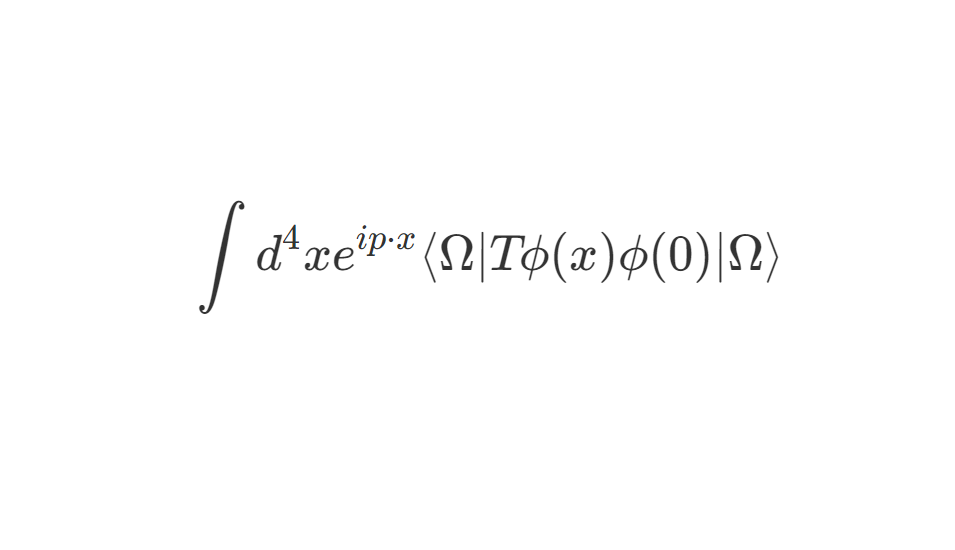费曼图与费曼规则
费曼图
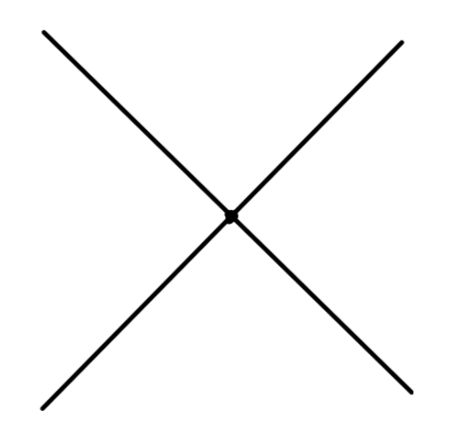
现在我们着手使用图形语言来计算关联函数。最简单的例子:
⟨0∣T{ϕ(x)ϕ(y)}∣0⟩=DF(x−y)(1)
我们表示为:

Fig1:自由两点关联函数
这就是 费曼图 Feynman diagram,这个图的值就是 (1)。我们现在将抽象的公式用直观的图表示,我们将会看到这种图形语言具有很多好处。
考虑更复杂一点的情况:
⟨0∣T{ϕ1ϕ2ϕ3ϕ4}∣0⟩=DF(x1−x2)DF(x3−x4)+DF(x1−x3)DF(x2−x4)+DF(x1−x4)DF(x2−x3)
这里 ϕ1 是 ϕ(x1) 的简写。
我们表示为:
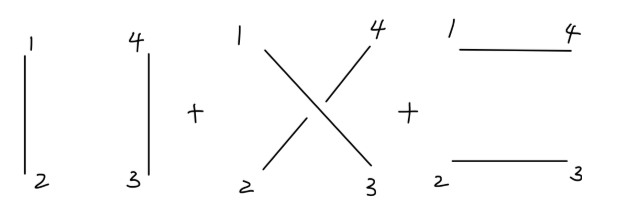
Fig2:自由四点关联函数
现在我们考虑存在相互作用后的关联函数:
⟨Ω∣T{ϕ(x)ϕ(y)}∣Ω⟩=⟨0∣T{exp(−i∫−∞∞dtHI(t))}∣0⟩⟨0∣T{ϕI(x)ϕI(y)exp(−i∫−∞∞dtHI(t))∣0⟩(2)
我们现在暂时忽略分母部分,仅仅讨论分子部分的计算。当相互作用很弱时,我们可以将分子中的指数部分作幂级数展开:
⟨0∣T{ϕ(x)ϕ(y)+ϕ(x)ϕ(y)[−i∫dtHI(t)]+⋯}∣0⟩(3)
对于 ϕ4 理论,相互作用形式为:
HI=∫4!λϕ4(z)d3z(4)
(3) 中的零阶项就是自由两点关联函数。一阶项为:
==⟨0∣T{ϕ(x)ϕ(y)(−i)∫dt∫4!λϕ4(z)d3z}∣0⟩⟨0∣T{ϕ(x)ϕ(y)(−i)∫4!λϕ4(z)d4z}∣0⟩⟨0∣T{ϕ(x)ϕ(y)(4!−iλ)∫ϕ(z)ϕ(z)ϕ(z)ϕ(z)d4z}∣0⟩(5)
只有其中的场量全部进行缩并,才可能得到非零的真空期望值。利用 wick 定理可得:共有以下两类有贡献的缩并方式:
- ϕ(x),ϕ(y) 缩并,ϕ(z) 间两两缩并。例如:
=⟨0∣ϕ∙(x)ϕ∙(y)(4!−iλ)∫ϕ∙∙(z)ϕ∙∙(z)ϕ(3∙)(z)ϕ(3∙)(z)d4z}∣0⟩4!−iλDF(x−y)∫d4zDF(z−z)DF(z−z)
等价的缩并方式数目为:
C22A22C24=3
可以使用费曼图表示为:
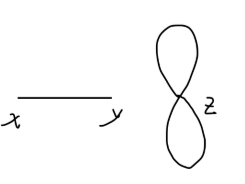
Fig3:ϕ4 两点关联函数一阶项:第一种缩并方式
- ϕ(x),ϕ(y) 分别与 ϕ(z) 缩并,剩下的两个 ϕ(z) 缩并。例如:
=⟨0∣ϕ∙(x)ϕ∙∙(y)(4!−iλ)∫ϕ∙(z)ϕ∙∙(z)ϕ(3∙)(z)ϕ(3∙)(z)d4z}∣0⟩4!−iλ∫d4zDF(x−z)DF(y−z)DF(z−z)
等价的缩并方式数目为:
C14C13=12
可以使用费曼图表示为:
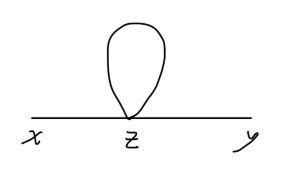
Fig4:ϕ4 两点关联函数一阶项:第二种缩并方式
那么 (5) 式可以用费曼图表示为:
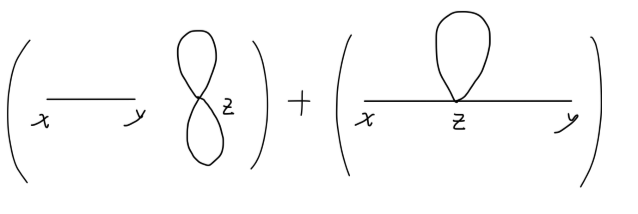
Fig5:ϕ4 两点关联函数一阶项
掌握这种方法后,我们可以用费曼图去计算微扰论任意阶的结果。例如 ϕ4 理论三阶微扰如下缩并:
⟨0∣ϕ∙(x)ϕ⋆(y)3!1(4!−iλ)3∫d4zϕ∙ϕ∙∙ϕ∙∙ϕ(3∙)∫d4wϕ(3∙)ϕ⋆ϕ⋆⋆ϕ(3⋆)∫d4uϕ⋆⋆ϕ⋆⋆ϕ(4⋆)ϕ(4⋆)
等价的缩并方式数目为:
A33C14C23C14C13C24C12=10368
其中 A33 代表了三个顶点 z,w,u 之间的置换。
利用费曼图表示为:
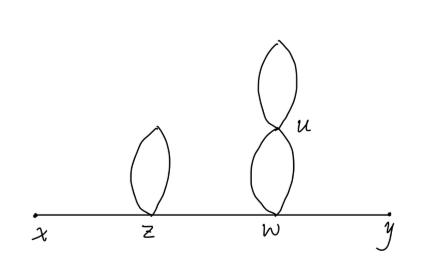
Fig6:ϕ4 两点关联函数三阶项的一种贡献
所有具有该结构的图都是等价的。现在我们来看,费曼图的结构是比某种具体的缩并方式更为普遍的东西。
费曼规则
我们已经介绍了从解析表达式到费曼图,那么我们现在反过来问:如何从费曼图得到解析表达式?我们以 ϕ4 理论为例回答这个问题。
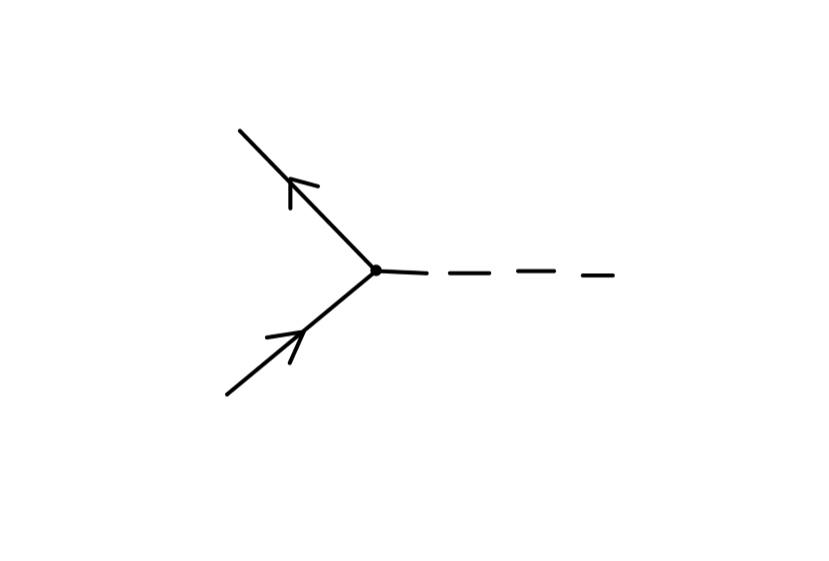
首先观察 ϕ4 理论的费曼图,如 Fig6 中出现的元素:
- 顶点 vertex
- 传播子 propagator
- 外部点 external point
Fig6 的值中出现的元素为:
- 积分 ∫d4z
- 耦合常数 λ/4!
- 传播子 DF(x−y)
- 对称因子 symmetry factor
现在我们想把费曼图中的元素与解析表达式关联起来。
首先来看对称因子。这应当体现为费曼图的对称度,即费曼图在某种操作下所体现出来的不变性,我们用 S 表示。不妨先考虑只有一个顶点的情况。若这个费曼图的对称因子为 1,也就是说:任意交换两条线我们发现,总共有 4! 种不同的缩并方式,但它们都对应于同一个费曼图,也就是有 4! 种等价的缩并方式。
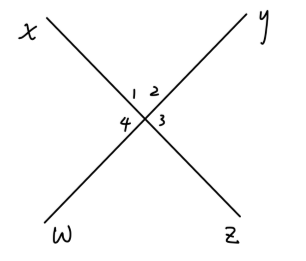
Fig7:对称度例1
再来看一些简单的例子:
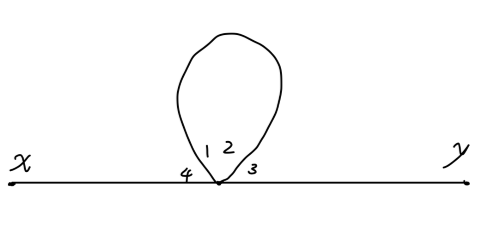
Fig8:对称度例2
交换线 1,2,图并不变化:有 S=2。此时,对于一种特定的缩并方式:交换线 1,2 已经不能给出新的缩并。所以:所有不同的缩并方式为 4!/2=12 种,它们对应的费曼图是相同的。
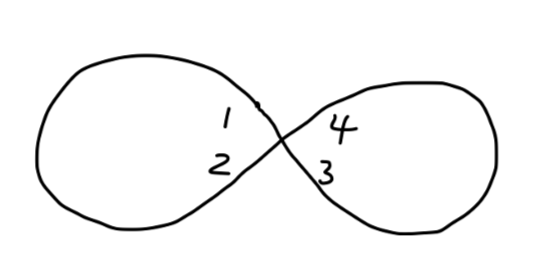
Fig9:对称度例3
分别交换线 1,2 或 3,4,图并不变化;另外整体交换 1,2 与 3,4,图均不变化:有 S=2×2×2=8。所有不同的缩并方式为 4!/8=3 种,它们对应的费曼图是相同的。
对于含有多个顶点的图来说,总的对称度应当为多个顶点对称度的乘积。
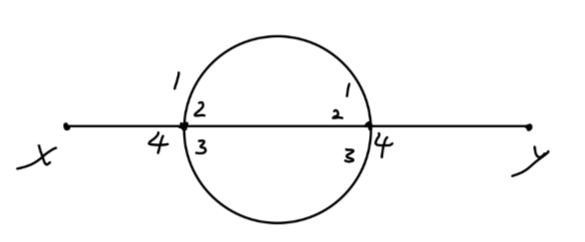
Fig10:对称度例4
交换线 1,2,3,图并不变化:有 S=3!=6。这个图包含两个顶点:若两个顶点的对称度为 1,得到的不同的缩并方式共有 4!×4! 种;额外的:需要考虑到交换这些顶点,也会给出不同的缩并方式。所以共有:
4!×4!×2!=1152
种缩并方式。而该图所对应等价的缩并数目为:
1152/6=192
一般来说:一个含有 n 个顶点的图所可能具有的最大不同的缩并方式数目为:
(4!)nn!
对于一个对称度为 S 的图,那么其对应的等价缩并数目为:
(4!)nn!/S
对所有不同结构的费曼图求和后,得到所有可能的缩并数目为:
(4!)nn!i∑Si−1(6)
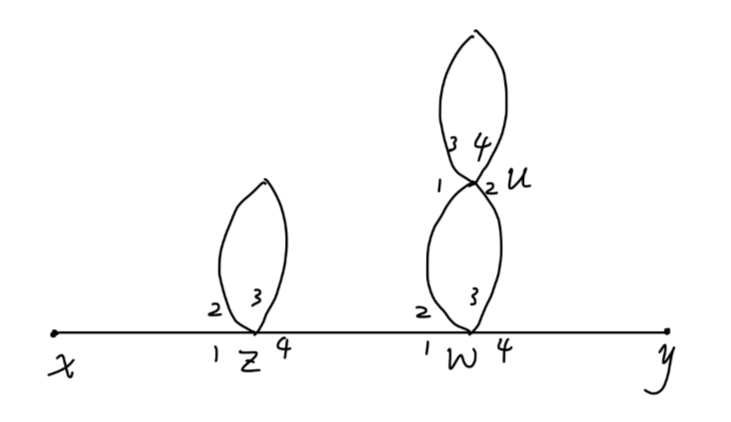
Fig11:对称度例5
以下操作均不改变图:
- 交换 z 顶点线 2,3:S1=2
- 交换 w 顶点线 2,3:S2=2
- 交换 u 顶点线 2,3:S3=2
得到:
S=S1S2S3=8
另外顶点数 n=3,于是等价缩并数目为:
8(4!)3×3!=10368
传播子的对应关系是最明显的,即

Fig12:传播子
其值为:
DF(x−y)
再来看顶点:
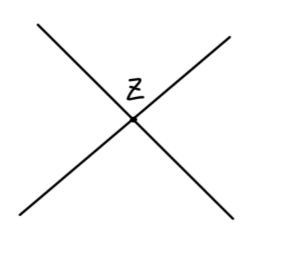
Fig13:顶点
在 ϕ4 理论中,顶点应当对应于:
∫4!−iλd4z(7)
由于最后我们要乘以等价缩并数,而 (6) 中正好包含 n 个 4! 因子。因此我们可以将这个因子吸收进入顶点对应的数学表达式:
∫−iλd4z(8)
则最后乘以的因子要修改为:
Sn!
若不认为顶点可以交换(提前标好了字母),此时只需除以对称因子 S。
对于外部点:

Fig14:外部点
我们简单规定其值为 1。
我们将以上讨论总结为 ϕ4 理论的 费曼规则 Feynman rules:
- 传播子

值为:
DF(x−y)
- 顶点

值为:
∫−iλd4z
- 外部点

值为:
1
我们称之前的费曼规则为 坐标空间中的费曼规则 position-space Feynman rules。现在我们来推导 动量空间中的费曼规则 momentum-space Feynman rules。我们需要重新赋予费曼图中各个元素的意义。
考虑到Klein-Gordon 场的费曼传播子的形式为:
DF(x−y)=∫(2π)4d4pp2−m2+iϵie−ip(x−y)
我们首先规定:
传播子
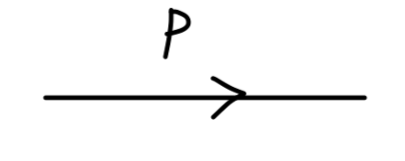
Fig15:传播子
的值为
p2−m2+iϵi
我们先将对动量的积分放在一边。对于费曼传播子中出现的指数项:
e−ip(x−y)=e−ipxeipy
我们将其与传播子所连接起的两点 x,y 关联起来。
那么对于外部点
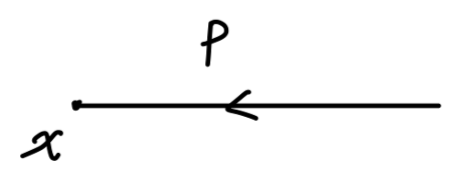
Fig16:外部点
其值为:
e−ipx
对于顶点来说,需要对坐标进行积分
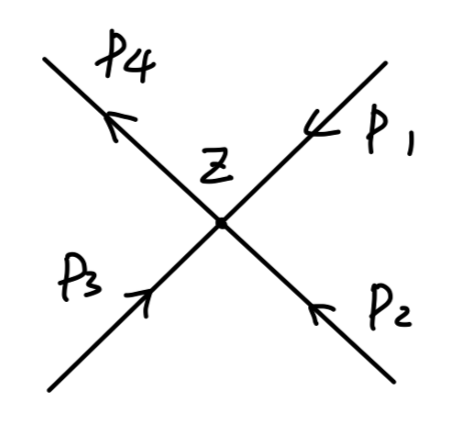
Fig17:顶点
可得其值为:
=−iλ∫d4ze−ip1ze−ip2ze−ip3ze+ip4z−iλ(2π)4δ(−p1−p2−p3+p4)
可得:顶点保证动量守恒。其中每个 δ 函数可以消去一个对动量的积分,最后我们只需要对那些未确定的动量进行积分,再除以对称因子。
我们将以上讨论总结为:
ϕ4 理论动量空间中的费曼规则

值为:
p2−m2+iϵi
值为:
−iλ

值为:
e−ip⋅x
∫(2π)4d4p
两点关联函数的计算
接下来,我们要利用费曼图去推导一个很有用的等式。我们先将遇到的费曼图进行分类:
- 连通图 connected diagram:图中任意两点都是连通的。
- 非连通图 disconnected diagram:存在两点不相连通。
例如:

是连通图。
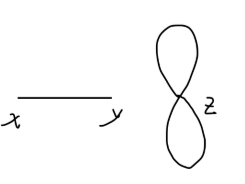
是非连通图,它由两个连通的部分组成。
在 ϕ4 理论两点关联函数的计算中,一个费曼图总有两个外部点。那么一般情况下,一个典型的两点关联函数的费曼图为:

Fig18:两点关联函数的费曼图
它是由一个具有两个外部点的连通部分与任意个不包含外点的连通部分组成的非连通图。对于第二部分,我们设其值为 Vi,i 表示某一种无外部点连通图。设该费曼图由一个两外部点连通部分和 ni 个值为 Vi 的无外点连通部分组成。那么,该费曼图的值为:
(value of connected piece)⋅i∏ni!1(Vi)ni
两点关联函数的值是对所有如此的费曼图的求和:
connected pieces∑all {ni}∑{value ofconnected piece}×i∏ni!1(Vi)ni=(∑connected)×all {ni}∑i∏ni!1(Vi)ni=(∑connected)×i∏ni∑ni!1(Vi)ni=(∑connected)×i∏exp(Vi)=(∑connected)×exp(i∑Vi)
其中 ∑connected 是对所有具有两个外部点的连通图的求和。
两点关联函数(准确说是分子部分):
⟨0∣T{ϕ(x)ϕ(y)exp[−i∫−∞∞dtHI(t)]}∣0⟩
可以用费曼图表示为:
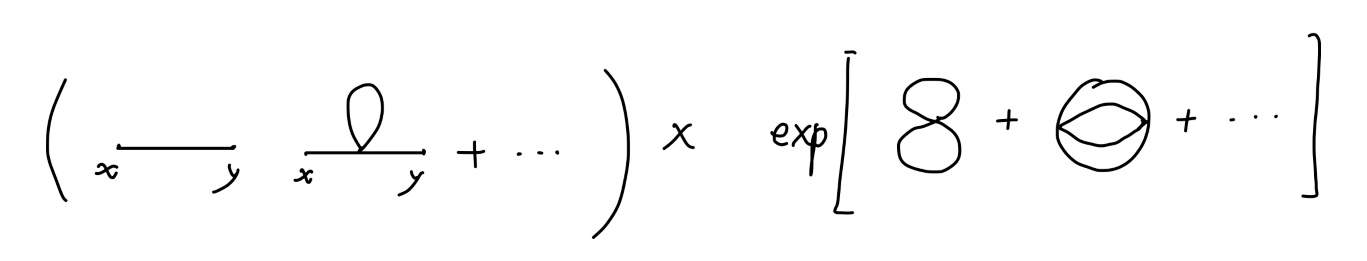
我们之前一直忽略的两点关联函数分母部分:
⟨0∣T{exp[−i∫−∞∞dtHI(t)]}∣0⟩
不难得到其值为:
exp(i∑Vi)
可以用费曼图表示为:
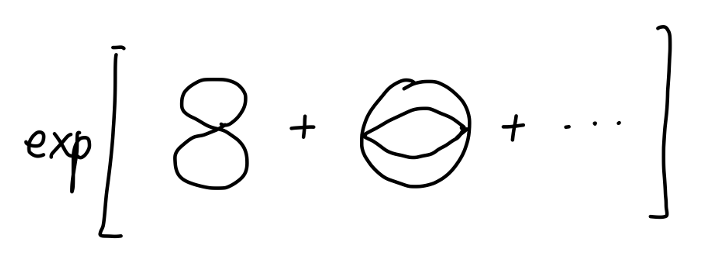
于是两点关联函数的值为:
⟨Ω∣T{ϕ(x)ϕ(y)}∣Ω⟩=∑connected(9)
可以用费曼图表示为:
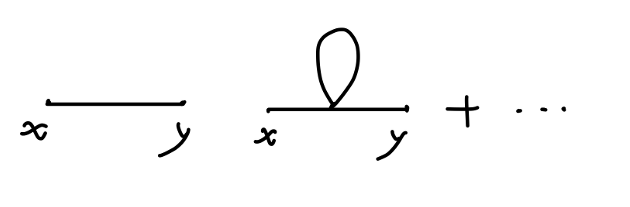
我们可以推到更高阶的关联函数上去。所有的奇数阶关联函数显然为零。对于偶数阶,例如四阶关联函数。它的值应当是那些:总共具有四个外部点(且不包含没有外部点的连通部分)的费曼图的总和。即: