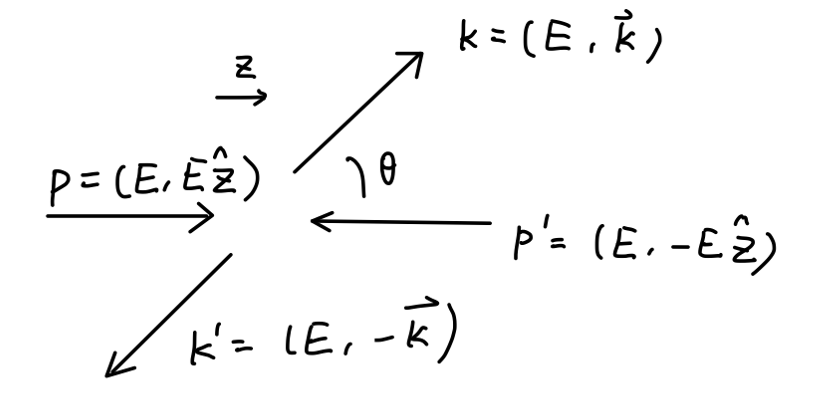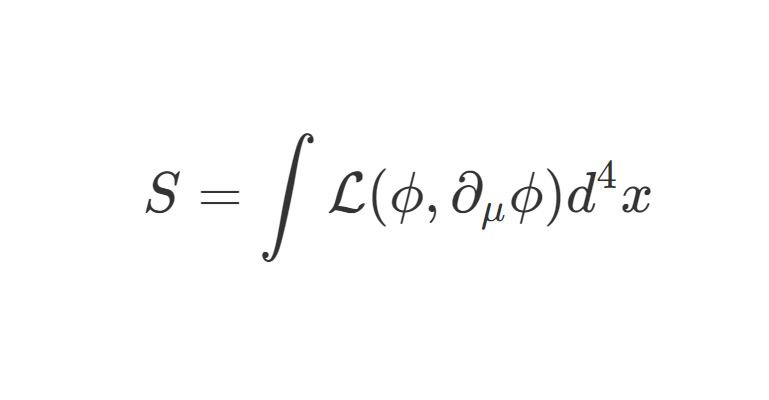现在，我们着手进行一些 QED 的计算。为了方便之后的计算，我们首先介绍 Trace Technology，即有关 Dirac 矩阵及其乘积的迹的计算。

Trace Technology

Dirac 矩阵的性质为：

{γμ,γν}=2gμν×1\{\gamma^{\mu},\gamma^{\nu}\} = 2g^{\mu\nu}\times \bm{1}

现在进行迹的计算：

  • tr(1)=4\mathrm{tr}(\bm{1}) = 4

  • tr(γμ)\mathrm{tr}(\gamma^{\mu})

tr(γμ)=tr(γ5γ5γμ)=−tr(γ5γμγ5)=−tr(γ5γ5γμ)=−tr(γμ)⇒tr(γμ)=0\begin{aligned} \mathrm{tr}(\gamma^{\mu}) &= \mathrm{tr}(\gamma^5\gamma^5\gamma^{\mu})\\ &=-\mathrm{tr}(\gamma^5\gamma^{\mu}\gamma^5)\\ &=-\mathrm{tr}(\gamma^5\gamma^5\gamma^{\mu})\\ &= - \mathrm{tr}(\gamma^{\mu}) \Rightarrow \mathrm{tr}(\gamma^{\mu})=0\\ \end{aligned}

上述推导应用了反对易关系：{γ5,γμ}=0\{\gamma^5,\gamma^{\mu}\}=0 与迹的性质：tr(ABC)=tr(CAB)\mathrm{tr}(ABC) = \mathrm{tr}(CAB)

  • tr(γμγν)\mathrm{tr}(\gamma^{\mu}\gamma^{\nu})

tr(γμγν)=tr(2gμν⋅1−γνγμ)=8gμν−tr(γμγν)\begin{aligned} \mathrm{tr}(\gamma^{\mu}\gamma^{\nu}) &= \mathrm{tr}(2g^{\mu\nu}\cdot\bm{1} - \gamma^{\nu}\gamma^{\mu})\\ &= 8g^{\mu\nu} - \mathrm{tr}(\gamma^{\mu}\gamma^{\nu})\\ \end{aligned}

推得：

tr(γμγν)=4gμν\mathrm{tr}(\gamma^{\mu}\gamma^{\nu}) = 4g^{\mu\nu}

任何偶数个 γ\gamma 矩阵的缩并都可以通过类似技巧得到，例如：

tr(γμγνγργσ)=tr(2gμνγργσ−γνγμγργσ)=tr(2gμνγργσ−γν2gμργσ+γνγργμγσ)=tr(2gμνγργσ−γν2gμργσ+γνγρ2gμσ−γνγργσγμ)=8(gμνgρσ−gμρgνσ+gνρgμσ)−tr(γμγνγργσ)\begin{aligned} \mathrm{tr}(\gamma^{\mu}\gamma^{\nu}\gamma^{\rho}\gamma^{\sigma}) &= \mathrm{tr}(2g^{\mu\nu}\gamma^{\rho}\gamma^{\sigma} - \gamma^{\nu}\gamma^{\mu}\gamma^{\rho}\gamma^{\sigma})\\ &=\mathrm{tr}(2g^{\mu\nu}\gamma^{\rho}\gamma^{\sigma} - \gamma^{\nu}2g^{\mu\rho}\gamma^{\sigma} + \gamma^{\nu}\gamma^{\rho}\gamma^{\mu}\gamma^{\sigma})\\ &=\mathrm{tr}(2g^{\mu\nu}\gamma^{\rho}\gamma^{\sigma} - \gamma^{\nu}2g^{\mu\rho}\gamma^{\sigma} + \gamma^{\nu}\gamma^{\rho}2g^{\mu\sigma}-\gamma^{\nu}\gamma^{\rho}\gamma^{\sigma}\gamma^{\mu})\\ &= 8(g^{\mu\nu}g^{\rho\sigma} - g^{\mu\rho}g^{\nu\sigma} + g^{\nu\rho}g^{\mu\sigma}) - \mathrm{tr}(\gamma^{\mu}\gamma^{\nu}\gamma^{\rho}\gamma^{\sigma}) \end{aligned}

得到：

tr(γμγνγργσ)=4(gμνgρσ−gμρgνσ+gνρgμσ)\mathrm{tr}(\gamma^{\mu}\gamma^{\nu}\gamma^{\rho}\gamma^{\sigma}) = 4(g^{\mu\nu}g^{\rho\sigma} - g^{\mu\rho}g^{\nu\sigma} + g^{\nu\rho}g^{\mu\sigma})

可以得到：

tr(γ5)=tr(iγ0γ1γ2γ3)=0\mathrm{tr}(\gamma^5) = \mathrm{tr}(i\gamma^0\gamma^1\gamma^2\gamma^3) = 0

  • tr(γμγνγργσγ5)=−4iϵμνρσ\mathrm{tr}(\gamma^{\mu}\gamma^{\nu}\gamma^{\rho}\gamma^{\sigma}\gamma^5) = -4i\epsilon^{\mu\nu\rho\sigma}

ϵμνρσ\epsilon^{\mu\nu\rho\sigma} 对于参数 (μνρσ)=(0123)(\mu\nu\rho\sigma)=(0123) 及其偶置换取 +1+1，其奇置换取 −1-1。并且具有以下性质：

ϵαβγδϵαβγδ=−24ϵαβγμϵαβγν=−6δ  νμϵαβμνϵαβρσ=−2(δ  ρμδ  σν−δ  σμδ  ρν)\begin{aligned} &\epsilon^{\alpha\beta\gamma\delta}\epsilon_{\alpha\beta\gamma\delta} = -24\\ &\epsilon^{\alpha\beta\gamma\mu}\epsilon_{\alpha\beta\gamma\nu} = -6\delta^{\mu}_{\ \ \nu}\\ &\epsilon^{\alpha\beta\mu\nu}\epsilon_{\alpha\beta\rho\sigma} = -2(\delta^{\mu}_{\ \ \rho}\delta^{\nu}_{\ \ \sigma}-\delta^{\mu}_{\ \ \sigma}\delta^{\nu}_{\ \ \rho}) \end{aligned}

注意：

ϵαβγδ=gαα′gββ′gγγ′gδδ′ϵα′β′γ′δ′=−ϵαβγδ\epsilon_{\alpha\beta\gamma\delta} = g_{\alpha\alpha'}g_{\beta\beta'} g_{\gamma\gamma'} g_{\delta\delta'} \epsilon^{\alpha'\beta'\gamma'\delta'} = - \epsilon^{\alpha\beta\gamma\delta}

另外一个有用的关系让我们可以调换迹中 γ\gamma 矩阵的顺序，即

tr(γμγν⋯ )=tr(⋯γνγμ)\begin{aligned} \mathrm{tr}(\gamma^{\mu}\gamma^{\nu}\cdots) &= \mathrm{tr}(\cdots\gamma^{\nu}\gamma^{\mu}) \end{aligned}

我们可以利用电荷共轭变换的性质：

C2=1,CγμC=−(γμ)TC^2=1,\quad C\gamma^{\mu}C = -(\gamma^{\mu})^T

可得：

tr(γμγν⋯ )=tr(CγμCCγνC⋯ )=(−1)ntr[(γμ)T(γν)T⋯ ]=tr(⋯γνγμ)\begin{aligned} \mathrm{tr}(\gamma^{\mu}\gamma^{\nu}\cdots) &= \mathrm{tr}(C\gamma^{\mu}CC\gamma^{\nu}C\cdots)\\ &=(-1)^n\mathrm{tr}[(\gamma^{\mu})^T(\gamma^{\nu})^T\cdots]\\ &=\mathrm{tr}(\cdots\gamma^{\nu}\gamma^{\mu})\\ \end{aligned}

在求迹运算前，提前处理一些缩并可以简化计算。

  • γμγμ\gamma^{\mu}\gamma_{\mu}

γμγμ=γμγνgμν=12γμγνgμν+12γνγμgνμ=12γμγνgμν+12γνγμgμν=12{γμ,γν}gμν=gμνgμν=4\begin{aligned} \gamma^{\mu}\gamma_{\mu} &= \gamma^{\mu}\gamma^{\nu}g_{\mu\nu}\\ &= \frac{1}{2}\gamma^{\mu}\gamma^{\nu}g_{\mu\nu} + \frac{1}{2}\gamma^{\nu}\gamma^{\mu}g_{\nu\mu}\\ &=\frac{1}{2}\gamma^{\mu}\gamma^{\nu}g_{\mu\nu} + \frac{1}{2}\gamma^{\nu}\gamma^{\mu}g_{\mu\nu}\\ &=\frac{1}{2}\{\gamma^{\mu},\gamma^{\nu}\}g_{\mu\nu}\\ &=g^{\mu\nu}g_{\mu\nu}\\ &= 4\\ \end{aligned}

  • γμγνγμ\gamma^{\mu}\gamma^{\nu}\gamma_{\mu}

γμγνγμ=(2gμν−γνγμ)γμ=2γν−4γν=−2γν\begin{aligned} \gamma^{\mu}\gamma^{\nu}\gamma_{\mu} &= (2g^{\mu\nu} - \gamma^{\nu}\gamma^{\mu})\gamma_{\mu}\\ &= 2\gamma^{\nu} - 4\gamma^{\nu} = -2\gamma^{\nu}\\ \end{aligned}

  • γμγνγργμ\gamma^{\mu}\gamma^{\nu}\gamma^{\rho}\gamma_{\mu}

γμγνγργμ=(2gμν−γνγμ)γργμ=2γργν−γν(2gμρ−γργμ)γμ=2γργν−2γνγρ+4γνγρ=2{γρ,γν}=4gρν\begin{aligned} \gamma^{\mu}\gamma^{\nu}\gamma^{\rho}\gamma_{\mu} &= (2g^{\mu\nu}-\gamma^{\nu}\gamma^{\mu})\gamma^{\rho}\gamma_{\mu}\\ &=2\gamma^{\rho}\gamma^{\nu} - \gamma^{\nu} (2g^{\mu\rho} - \gamma^{\rho}\gamma^{\mu})\gamma_{\mu}\\ &= 2\gamma^{\rho}\gamma^{\nu} - 2\gamma^{\nu}\gamma^{\rho} + 4\gamma^{\nu}\gamma^{\rho}\\ &=2\{\gamma^{\rho},\gamma^{\nu}\}\\ &=4g^{\rho\nu} \end{aligned}

  • γμγνγργσγμ\gamma^{\mu}\gamma^{\nu}\gamma^{\rho}\gamma^{\sigma}\gamma_{\mu}

γμγνγργσγμ=(2gμν−γνγμ)γργσγμ=2γργσγν−4γνgρσ=2γργσγν−2(γργσ+γσγρ)γν=−2γσγργν\begin{aligned} \gamma^{\mu}\gamma^{\nu}\gamma^{\rho}\gamma^{\sigma}\gamma_{\mu} &= (2g^{\mu\nu}-\gamma^{\nu}\gamma^{\mu})\gamma^{\rho}\gamma^{\sigma}\gamma_{\mu}\\ &=2\gamma^{\rho}\gamma^{\sigma}\gamma^{\nu} - 4\gamma^{\nu} g^{\rho\sigma}\\ &=2\gamma^{\rho}\gamma^{\sigma}\gamma^{\nu} - 2(\gamma^{\rho}\gamma^{\sigma} + \gamma^{\sigma}\gamma^{\rho})\gamma^{\nu}\\ &= -2\gamma^{\sigma}\gamma^{\rho}\gamma^{\nu}\\ \end{aligned}

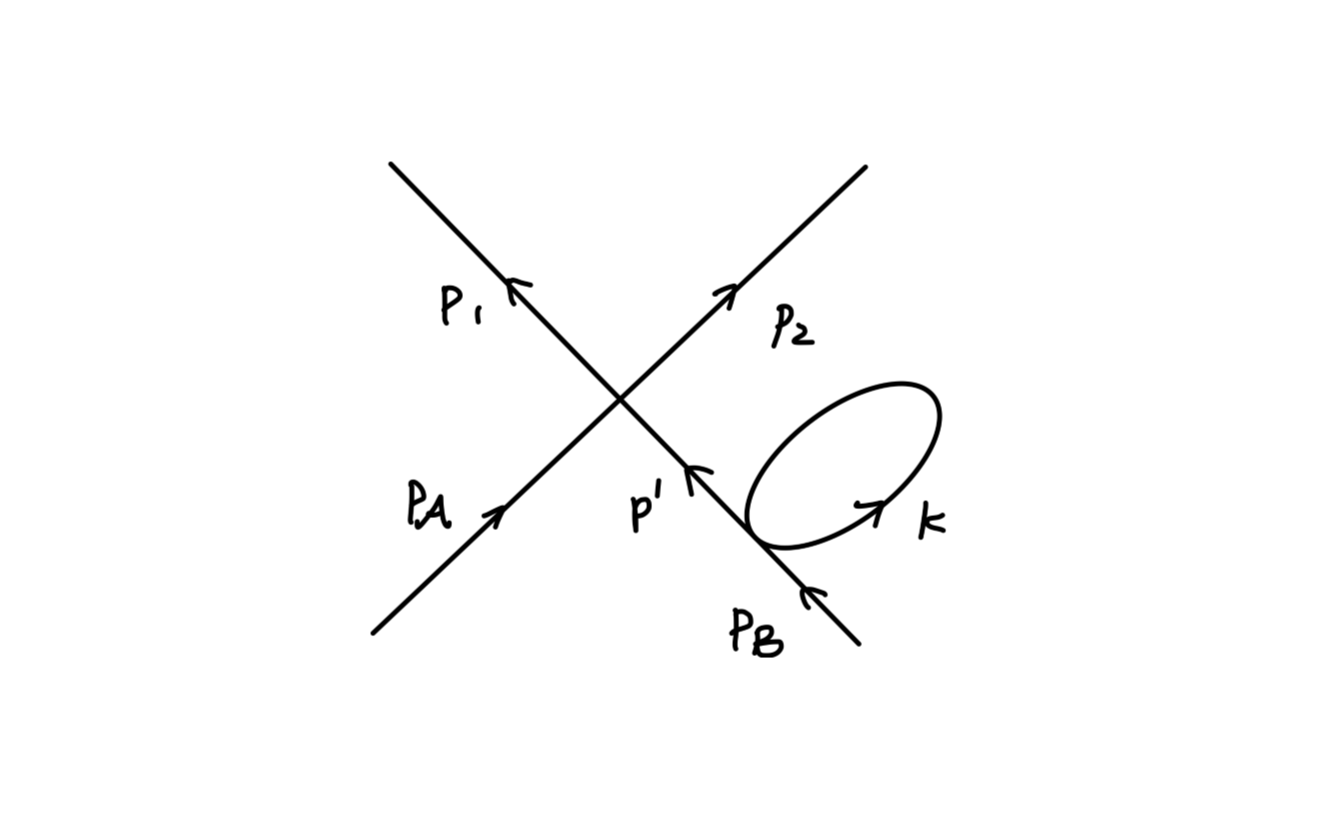
e+e−→μ+μ−e^{+}e^{-}\rightarrow \mu^{+}\mu^{-}

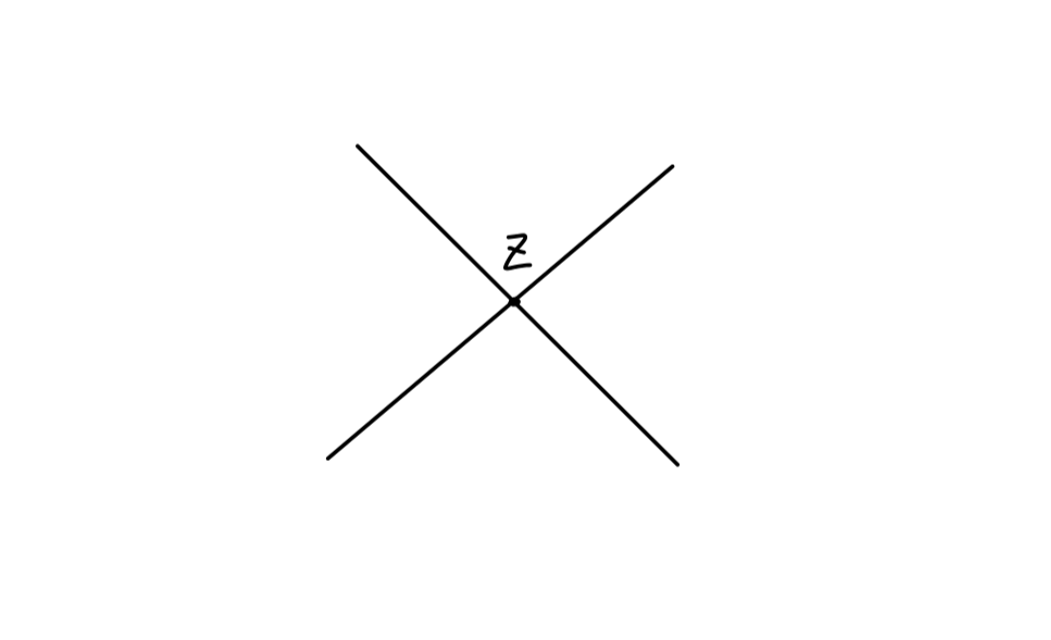
e+e−→μ+μ−e^{+}e^{-}\rightarrow \mu^{+}\mu^{-} 是最简单的 QED 过程。其费曼图为：

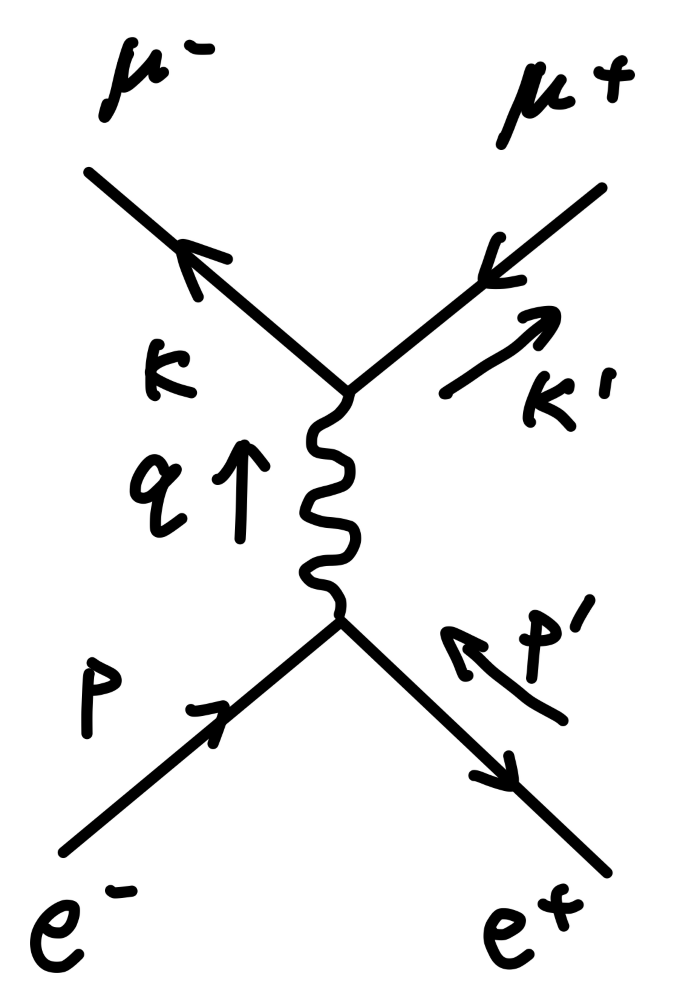
其跃迁矩阵元为：

iM=vˉs(p′)(−ieγμ)us(p)(−igμνq2)uˉr(k)(−ieγν)vr′(k′)\begin{aligned} i\mathcal{M} = \bar{v}^s(p')(-ie\gamma^{\mu})u^s(p)(-\frac{ig_{\mu\nu}}{q^2})\bar{u}^r(k)(-ie\gamma^\nu)v^{r'}(k') \end{aligned}

整理得到：

M(e−(p)e+(p′)→μ−(k)μ+(k′))=ie2q2(vˉ(p′)γμu(p))(uˉ(k)γμv(k′))\mathcal{M}(e^{-}(p)e^{+}(p')\rightarrow \mu^-(k)\mu^+(k'))= \frac{ie^2}{q^2}(\bar{v}(p')\gamma^{\mu}u(p))(\bar{u}(k)\gamma_{\mu}v(k'))

跃迁矩阵元的模方为：

∣M∣2=e4q4(vˉ(p′)γμu(p)uˉ(p)γνv(p′))(uˉ(k)γμv(k′)vˉ(k′)γνu(k))(1)\begin{aligned} |\mathcal{M}|^2 = \frac{e^4}{q^4}(\bar{v}(p')\gamma^{\mu}u(p)\bar{u}(p)\gamma^{\nu}v(p'))(\bar{u}(k)\gamma_{\mu}v(k')\bar{v}(k')\gamma_{\nu}u(k)) \end{aligned}\tag{1}

在实验中，我们很难控制自旋态。在大多数实验中，我们通常是制备一些未极化的初态，这意味着它处于任何自旋的概率是一样的。我们应当对所有可能的自旋态求平均。对应求得的散射截面称为 非极化截面 unpolarized cross section。

这意味着我们要计算以下物理量：

12∑s12∑s′∑r∑r′∣M(s,s′→r,r′)∣2(2)\frac{1}{2}\sum_{s}\frac{1}{2}\sum_{s'}\sum_{r}\sum_{r'}|\mathcal{M}(s,s'\rightarrow r,r')|^2 \tag{2}

利用完备性关系：

∑sus(p)uˉs(p)=γ⋅p+m∑svs(p)vˉs(p)=γ⋅p−m\begin{aligned} &\sum_s u^s(p)\bar{u}^s(p) = \gamma\cdot p + m\\ &\sum_s v^s(p)\bar{v}^s(p) = \gamma\cdot p - m\\ \end{aligned}

可得：

∑ss′(vˉs′(p′)γμus(p)uˉs(p)γνvs′(p′))=∑s′(vˉs′(p′)γμ(∑sus(p)uˉs(p))γνvs′(p′))=∑s′(vˉas′(p′)γabμ(γ⋅p+m)bcγcdνvds′(p′))=∑s′((vds′(p′)vˉas′(p′))γabμ(γ⋅p+m)bcγcdν)=(γ⋅p′−m)daγabμ(γ⋅p+m)bcγcdν=tr[(γ⋅p′−m)γμ(γ⋅p+m)γν](3)\begin{aligned} &\sum_{ss'}(\bar{v}^{s'}(p')\gamma^{\mu}u^s(p)\bar{u}^s(p)\gamma^{\nu}v^{s'}(p')) \\ &= \sum_{s'}(\bar{v}^{s'}(p')\gamma^{\mu}(\sum_{s} u^s(p)\bar{u}^s(p))\gamma^{\nu}v^{s'}(p'))\\ &=\sum_{s'}(\bar{v}^{s'}_a(p')\gamma^{\mu}_{ab}(\gamma\cdot p + m)_{bc}\gamma^{\nu}_{cd}v^{s'}_{d}(p'))\\ &=\sum_{s'}((v^{s'}_{d}(p')\bar{v}^{s'}_a(p'))\gamma^{\mu}_{ab}(\gamma\cdot p + m)_{bc}\gamma^{\nu}_{cd})\\ &=(\gamma\cdot p' - m)_{da}\gamma^{\mu}_{ab}(\gamma\cdot p + m)_{bc}\gamma^{\nu}_{cd}\\ &=\mathrm{tr}[(\gamma\cdot p' - m)\gamma^{\mu}(\gamma\cdot p + m)\gamma^{\nu}] \end{aligned}\tag{3}

代入 (2)(2) 式可得：

14∑ss′rr′∣M∣2=14e4q4(vˉ(p′)γμu(p)uˉ(p)γνv(p′))(uˉ(k)γμv(k′)vˉ(k′)γνu(k))=e44q2tr[(γ⋅p′−me)γμ(γ⋅p+me)γν]tr[(γ⋅k+mμ)γμ(γ⋅k′−mμ)γν]\begin{aligned} \frac{1}{4}\sum_{ss'rr'}|\mathcal{M}|^2 &= \frac{1}{4}\frac{e^4}{q^4}(\bar{v}(p')\gamma^{\mu}u(p)\bar{u}(p)\gamma^{\nu}v(p'))(\bar{u}(k)\gamma_{\mu}v(k')\bar{v}(k')\gamma_{\nu}u(k))\\ &= \frac{e^4}{4q^2}\mathrm{tr}[(\gamma\cdot p' - m_e)\gamma^{\mu}(\gamma\cdot p + m_e)\gamma^{\nu}]\mathrm{tr}[(\gamma\cdot k + m_{\mu})\gamma_{\mu}(\gamma\cdot k' - m_{\mu})\gamma_{\nu}] \end{aligned}

现在我们来计算式 (3)(3)，可以得到：

tr[(γ⋅p′−me)γμ(γ⋅p+me)γν]=tr[(γρpρ′−me)γμ(γσpσ+me)γν]=tr(γργμγσγνpρ′pσ+γργμγνpσ′me−γμγσγνpσme−me2γμγν)=4(gρμgσν−gρσgμν+gρνgμσ)pρ′pσ−4me2gμν=4(p′μpν+p′νpμ−gμν(p′⋅p+me2))\begin{aligned} &\mathrm{tr}[(\gamma\cdot p' - m_e)\gamma^{\mu}(\gamma\cdot p + m_e)\gamma^{\nu}]\\ &=\mathrm{tr}[(\gamma^{\rho} p'_{\rho} - m_e)\gamma^{\mu}(\gamma^{\sigma} p_{\sigma} + m_e)\gamma^{\nu}]\\ &= \mathrm{tr}(\gamma^{\rho}\gamma^{\mu}\gamma^{\sigma}\gamma^{\nu}p'_{\rho}p_{\sigma} + \gamma^{\rho}\gamma^{\mu}\gamma^{\nu}p'_{\sigma}m_e - \gamma^{\mu}\gamma^{\sigma}\gamma^{\nu}p_{\sigma}m_e - m_e^2 \gamma^{\mu}\gamma^{\nu})\\ &= 4(g^{\rho\mu}g^{\sigma\nu} - g^{\rho\sigma}g^{\mu\nu}+ g^{\rho\nu}g^{\mu\sigma})p'_{\rho}p_{\sigma} - 4m_e^2g^{\mu\nu}\\ &=4(p'^{\mu}p^{\nu}+p'^{\nu}p^{\mu} - g^{\mu\nu}(p'\cdot p + m_e^2)) \end{aligned}

近似认为 me=0m_e =0，那么可得：

14∑spins∣M∣2=4e4q4(p′μpν+p′νpμ−gμν(p′⋅p+me2))(kμkν′+kνkμ′−gμν(k⋅k′+mμ2))=8e4q4((p′⋅k)(p⋅k′)+(p⋅k)(p′⋅k′)+mμ2(p⋅p′))(4)\begin{aligned} \frac{1}{4}\sum_{spins}|\mathcal{M}|^2&=\frac{4e^4}{q^4}(p'^{\mu}p^{\nu}+p'^{\nu}p^{\mu} - g^{\mu\nu}(p'\cdot p + m_e^2))(k_{\mu}k'_{\nu}+k_{\nu}k'_{\mu} - g_{\mu\nu}(k\cdot k' + m_{\mu}^2))\\ &= \frac{8e^4}{q^4}((p'\cdot k)(p\cdot k') + (p\cdot k)(p'\cdot k') + m_{\mu}^2(p\cdot p') ) \end{aligned}\tag{4}

考虑初态为正负电子对撞的情况。

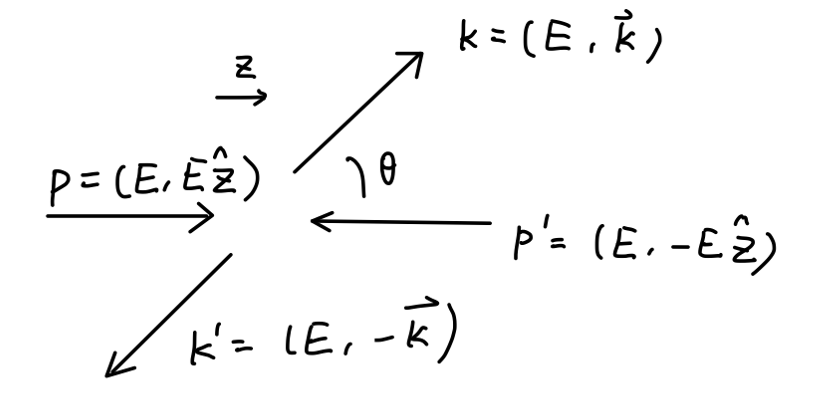
得到：

p′⋅k=p⋅k′=E2+E∣k∣cos⁡θp⋅k=p′⋅k′=E2−E∣k∣cos⁡θp⋅p′=2E2,q2=(p+p′)2=4E2(5)\begin{aligned} &p'\cdot k = p\cdot k' = E^2 + E|\bm{k}|\cos\theta\\ &p\cdot k = p'\cdot k' = E^2 - E|\bm{k}|\cos\theta\\ &p\cdot p' = 2E^2,\quad q^2 = (p+p')^2 = 4E^2 \end{aligned}\tag{5}

代入得到：

14∑spins∣M∣2=8e4q4((E2+E∣k∣cos⁡θ)2+(E2−E∣k∣cos⁡θ)2+2mμ2E2)=8e416E4(2E4+2E2(E2−mμ2)cos⁡2θ+2mμ2E2)=e4[(1+mμ2E2)+(1−mμ2E2)cos⁡2θ](6)\begin{aligned} \frac{1}{4}\sum_{spins}|\mathcal{M}|^2 &= \frac{8e^4}{q^4}((E^2 + E|\bm{k}|\cos\theta)^2 + (E^2 - E|\bm{k}|\cos\theta)^2 + 2m_{\mu}^2E^2 )\\ &= \frac{8e^4}{16E^4}(2E^4 + 2E^2(E^2-m_{\mu}^2)\cos^2\theta + 2m_{\mu}^2E^2)\\ &= e^4[(1+\frac{m_{\mu}^2}{E^2})+(1-\frac{m_{\mu}^2}{E^2})\cos^2\theta] \end{aligned}\tag{6}

相应的微分散射截面为：

dσdΩ=12Ecm2∣k∣16π2Ecm2⋅14∑spins∣M∣2=α24Ecm21−mμ2E2[(1+mμ2E2)+(1−mμ2E2)cos⁡2θ](7)\begin{aligned} \frac{d\sigma}{d\Omega} &= \frac{1}{2E_{cm}^2}\frac{|\bm{k}|}{16\pi^2E_{cm}^2}\cdot \frac{1}{4}\sum_{spins} |\mathcal{M}|^2\\ &= \frac{\alpha^2}{4E_{cm}^2}\sqrt{1-\frac{m_{\mu}^2}{E^2}}[(1+\frac{m_{\mu}^2}{E^2})+(1-\frac{m_{\mu}^2}{E^2})\cos^2\theta] \end{aligned}\tag{7}

通过积分得到总散射截面：

σtotal=4πα23Ecm21−mμ2E2(1+12mμ2E2)(8)\sigma_{total} = \frac{4\pi\alpha^2}{3E_{cm}^2}\sqrt{1-\frac{m_{\mu}^2}{E^2}}(1+\frac{1}{2}\frac{m^2_{\mu}}{E^2}) \tag{8}

在高能极限时（E≫mμE\gg m_{\mu}），相应的微分散射截面与总散射截面为：

dσdΩ=α24Ecm2(1+cos⁡2θ)σtotal=4πα23Ecm2(1−38(mμE)4−⋯ )(9)\begin{aligned} &\frac{d\sigma}{d\Omega} = \frac{\alpha^2}{4E_{cm}^2}(1+\cos^2\theta)\\ &\sigma_{total} = \frac{4\pi\alpha^2}{3E_{cm}^2}(1-\frac{3}{8}(\frac{m_{\mu}}{E})^4-\cdots) \end{aligned}\tag{9}

螺旋度结构

高能极限下 e+e−→μ+μ−e^{+}e^{-} \rightarrow \mu^+\mu^- 的微分散射截面是容易计算的，但却不好理解其中出现的 1+cos⁡2θ1+\cos^2\theta 因子。现在我们通过来计算各个自旋态对应的散射截面，即 极化截面 polarized cross section 来理解这件事。

对于无质量费米子，以下矩阵将 Dirac 旋量映射成 右手/左手旋量：

1+γ52=(0001)1−γ52=(1000)(10)\frac{1+\gamma^5}{2} = \begin{pmatrix} 0 & 0\\ 0 & 1\\ \end{pmatrix} \quad \frac{1-\gamma^5}{2} = \begin{pmatrix} 1 & 0\\ 0 & 0\\ \end{pmatrix}\tag{10}

我们现在对包含 Dirac 旋量跃迁矩阵元做如下替换，以用来计算对于右手旋量的跃迁矩阵元。

vˉ(p′)γμu(p)→vˉ(p′)γμ(1+γ52)u(p)(11)\bar{v}(p')\gamma^{\mu}u(p) \rightarrow \bar{v}(p')\gamma^{\mu}(\frac{1+\gamma^5}{2})u(p)\tag{11}

这里：

(1+γ52)u(p)(\frac{1+\gamma^5}{2})u(p)

成为一右手旋量。

(11)(11) 式还可以写为：

vˉ(p′)γμ(1+γ52)u(p)=v†(p′)(1+γ52)γ0γμu(p)(12)\bar{v}(p')\gamma^{\mu}(\frac{1+\gamma^5}{2})u(p) = v^\dagger(p')(\frac{1+\gamma^5}{2})\gamma^{0}\gamma^{\mu}u(p) \tag{12}

此时：

v†(p′)(1+γ52)v^\dagger(p')(\frac{1+\gamma^5}{2})

成为一右手旋量。于是我们得到：对于 u(p),v(p)u(p),v(p)，改变左手旋量的值对结果并无影响。

而注意到右手旋量 v(p)v(p) 对应于左手反粒子。因此我们说：只有正反粒子具有相反的螺旋度时，该项才对跃迁矩阵元有贡献。

考虑一个右手态电子与左手态反电子的贡献：

∑spins∣vˉ(p′)γμ(1+γ52)u(p)∣2=∑spins[vˉ(p′)γμ(1+γ52)u(p)][uˉ(p)γν(1+γ52)v(p′)]=tr((p′⋅γ)γμ(1+γ52)(p⋅γ)γν(1+γ52))=tr((p′⋅γ)γμ(p⋅γ)γν(1+γ52)2)=tr((p′⋅γ)γμ(p⋅γ)γν(1+γ52))=2(p′μpν+p′νpμ−gμνp⋅p′−iϵαμβνpα′pβ)\begin{aligned} \sum_{spins} |\bar{v}(p')\gamma^{\mu}(\frac{1+\gamma^5}{2})u(p)|^2&= \sum_{spins} [\bar{v}(p')\gamma^{\mu}(\frac{1+\gamma^5}{2})u(p)][\bar{u}(p)\gamma^{\nu}(\frac{1+\gamma^5}{2})v(p')]\\ &= \mathrm{tr}((p'\cdot\gamma)\gamma^{\mu}(\frac{1+\gamma^5}{2})(p\cdot\gamma)\gamma^{\nu}(\frac{1+\gamma^5}{2}))\\ &= \mathrm{tr}((p'\cdot\gamma)\gamma^{\mu}(p\cdot\gamma)\gamma^{\nu}(\frac{1+\gamma^5}{2})^2)\\ &= \mathrm{tr}((p'\cdot\gamma)\gamma^{\mu}(p\cdot\gamma)\gamma^{\nu}(\frac{1+\gamma^5}{2}))\\ &= 2(p'^{\mu}p^{\nu} + p'^{\nu}p^{\mu} -g^{\mu\nu}p\cdot p' - i\epsilon^{\alpha\mu\beta\nu}p'_{\alpha}p_{\beta}) \end{aligned}

考虑末态为右手态 μ−\mu^{-} 与左手态 μ+\mu^{+}：

∑spins∣uˉ(k)γμ(1+γ52)v(k′)∣2=2(kμkν′+kνkμ′−gμνk⋅k′−iϵρμσνkρk′σ)\sum_{spins} |\bar{u}(k)\gamma_{\mu}(\frac{1+\gamma^5}{2})v(k')|^2 = 2(k_{\mu}k'_{\nu} + k_{\nu}k'_{\mu} -g_{\mu\nu}k\cdot k' - i\epsilon_{\rho\mu\sigma\nu}k^{\rho}k'^{\sigma})

得到跃迁矩阵元为：

∣M∣2=4e4q4[2(p′μpν+p′νpμ−gμνp⋅p′−iϵαμβνpα′pβ)][2(kμkν′+kνkμ′−gμνk⋅k′−iϵρμσνkρk′σ)]=4e4q4[2(p⋅k)(p′⋅k′)+2(p⋅k′)(p′⋅k)−ϵαμβνϵαμβνpα′pβkρk′σ]=16e4q4(p⋅k′)(p′⋅k)=e4(1+cos⁡θ)2\begin{aligned} |\mathcal{M}|^2 &= \frac{4e^4}{q^4}[2(p'^{\mu}p^{\nu} + p'^{\nu}p^{\mu} -g^{\mu\nu}p\cdot p' - i\epsilon^{\alpha\mu\beta\nu}p'_{\alpha}p_{\beta})][2(k_{\mu}k'_{\nu} + k_{\nu}k'_{\mu} -g_{\mu\nu}k\cdot k' - i\epsilon_{\rho\mu\sigma\nu}k^{\rho}k'^{\sigma})]\\ &= \frac{4e^4}{q^4}[2(p\cdot k)(p'\cdot k') + 2(p\cdot k')(p'\cdot k) - \epsilon^{\alpha\mu\beta\nu}\epsilon_{\alpha\mu\beta\nu} p'_{\alpha} p_{\beta} k^{\rho} k'^{\sigma} ]\\ &= \frac{16e^4}{q^4}(p\cdot k')(p'\cdot k)\\ &= e^4(1+\cos\theta)^2\\ \end{aligned}

得到对应的微分散射截面为：

dσdΩ(eR−eL+→μR−μL+)=α24Ecm2(1+cos⁡θ)2(13)\frac{d\sigma}{d\Omega}(e^{-}_Re^+_{L} \rightarrow \mu^{-}_{R}\mu^{+}_{L}) = \frac{\alpha^2}{4E_{cm}^2}(1+\cos\theta)^2\tag{13}

同理，可以计算剩下三种情况的微分散射截面：

dσdΩ(eR−eL+→μL−μR+)=α24Ecm2(1−cos⁡θ)2dσdΩ(eL−eR+→μR−μL+)=α24Ecm2(1−cos⁡θ)2dσdΩ(eL−eR+→μL−μR+)=α24Ecm2(1+cos⁡θ)2(14)\begin{aligned} \frac{d\sigma}{d\Omega}(e^{-}_Re^+_{L} \rightarrow \mu^{-}_{L}\mu^{+}_{R}) = \frac{\alpha^2}{4E_{cm}^2}(1-\cos\theta)^2\\ \frac{d\sigma}{d\Omega}(e^{-}_Le^+_{R} \rightarrow \mu^{-}_{R}\mu^{+}_{L}) = \frac{\alpha^2}{4E_{cm}^2}(1-\cos\theta)^2\\ \frac{d\sigma}{d\Omega}(e^{-}_Le^+_{R} \rightarrow \mu^{-}_{L}\mu^{+}_{R}) = \frac{\alpha^2}{4E_{cm}^2}(1+\cos\theta)^2\\ \end{aligned}\tag{14}

现在我们考虑直接代入波函数的表达式计算跃迁矩阵元。

M=e2q2(vˉ(p′)γμu(p))(uˉ(k)γμv(k′))(15)\mathcal{M} = \frac{e^2}{q^2}(\bar{v}(p')\gamma^{\mu}u(p))(\bar{u}(k)\gamma_{\mu}v(k'))\tag{15}

在高能极限下：

u(p)=(p⋅σξp⋅σˉξ)⟶E→∞2E(12(1−p⋅σ)ξ12(1+p⋅σ)ξ)v(p)=(p⋅σξ−p⋅σˉξ)⟶E→∞2E(12(1−p⋅σ)ξ−12(1+p⋅σ)ξ)(16)\begin{aligned} u(p) &= \begin{pmatrix} \sqrt{p\cdot \sigma}\xi\\ \sqrt{p\cdot \bar{\sigma}}\xi\\ \end{pmatrix}\underset{E\rightarrow\infty}{\longrightarrow} \sqrt{2E}\begin{pmatrix} \frac{1}{2}(1-\bm{p}\cdot\bm{\sigma})\xi\\ \frac{1}{2}(1+\bm{p}\cdot\bm{\sigma})\xi\\ \end{pmatrix}\\ v(p) &= \begin{pmatrix} \sqrt{p\cdot \sigma}\xi\\ -\sqrt{p\cdot \bar{\sigma}}\xi\\ \end{pmatrix}\underset{E\rightarrow\infty}{\longrightarrow} \sqrt{2E}\begin{pmatrix} \frac{1}{2}(1-\bm{p}\cdot\bm{\sigma})\xi\\ -\frac{1}{2}(1+\bm{p}\cdot\bm{\sigma})\xi\\ \end{pmatrix}\\ \end{aligned}\tag{16}

p^⋅σ\hat{\bm{p}}\cdot\bm{\sigma} 正是螺旋度算符，对于右手正粒子来说：(p⋅σ)ξ=+ξ(\bm{p}\cdot\bm{\sigma})\xi = + \xi；对于左手正粒子来说：(p⋅σ)ξ=−ξ(\bm{p}\cdot\bm{\sigma})\xi = - \xi。对于反粒子来说会相反。

现在选取一个特定的初态。电子和反电子的动量 p,p′p,p' 分别指向 zz 轴的正、负方向，对于右手电子来说，自旋为：ξ=(10)\xi = \begin{pmatrix}1\\ 0\\ \end{pmatrix}；对于左手反电子来说，自旋为：ξ=(01)\xi = \begin{pmatrix}0\\ 1\\ \end{pmatrix}。

得到正/反粒子旋量为：

u(p)=2E(0010)v(p′)=2E(000−1)(17)\begin{aligned} u(p) = \sqrt{2E}\begin{pmatrix} 0 \\ 0 \\ 1 \\ 0 \\ \end{pmatrix}\qquad v(p') = \sqrt{2E}\begin{pmatrix} 0 \\ 0 \\ 0 \\ -1 \\ \end{pmatrix} \end{aligned} \tag{17}

得到：

vˉ(p′)γμu(p)=2E(0,−1)σμ(10)=−2E(0,1,i,0)(18)\bar{v}(p')\gamma^{\mu}u(p) = 2E\begin{pmatrix} 0,-1\\ \end{pmatrix}\sigma^{\mu}\begin{pmatrix} 1\\ 0\\ \end{pmatrix} = -2E(0,1,i,0) \tag{18}

考虑末态为：

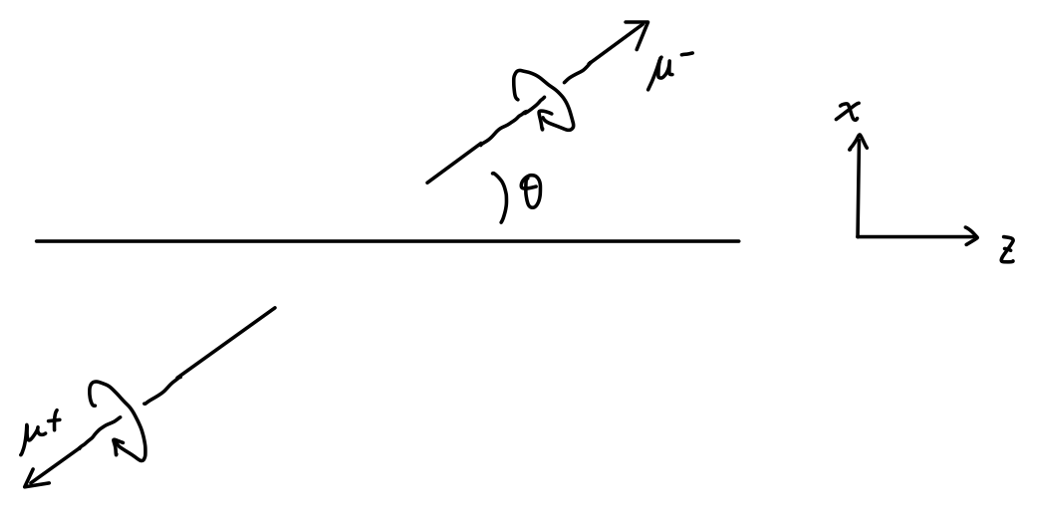
只需要在 xzxz 平面内做一个角度为 θ\theta 的旋转即可，可得：

uˉ(k)γμv(k′)=[vˉ(k′)γμu(k)]∗=[−2E(0,cos⁡θ,i,−sin⁡θ)]∗=−2E(0,cos⁡θ,−i,−sin⁡θ)(19)\begin{aligned} \bar{u}(k)\gamma^{\mu}v(k') &= [\bar{v}(k')\gamma^{\mu}u(k)]^*\\ &= [-2E(0,\cos\theta,i,-\sin\theta)]^*\\ &= -2E(0,\cos\theta,-i,-\sin\theta)\\ \end{aligned}\tag{19}

将 (18)(19)(18)(19) 代入 (15)(15) 得到：

M(eR−eL+→μR−μL+)=−e2(1+cos⁡θ)(20)\mathcal{M}(e^{-}_{R}e^+_L\rightarrow \mu_R^-\mu_L^+) = -e^2(1+\cos\theta) \tag{20}

类似的计算得到剩下三个跃迁矩阵元：

M(eL−eR+→μL−μR+)=−e2(1+cos⁡θ)M(eL−eR+→μL−μR+)=M(eR−eL+→μR−μL+)=−e2(1−cos⁡θ)(21)\begin{aligned} &\mathcal{M}(e^{-}_{L}e^+_R\rightarrow \mu_L^-\mu_R^+) = -e^2(1+\cos\theta)\\ &\mathcal{M}(e^{-}_{L}e^+_R\rightarrow \mu_L^-\mu_R^+)=\mathcal{M}(e^{-}_{R}e^+_L\rightarrow \mu_R^-\mu_L^+) = -e^2(1-\cos\theta)\\ \end{aligned} \tag{21}

非相对论极限

现在讨论在能量稍大于 mμm_{\mu} 时的散射截面。

dσdΩ=α24Ecm21−mμ2E2[(1+mμ2E2)+(1−mμ2E2)cos⁡2θ]⟶∣k∣→0α24Ecm2∣k∣E⋅2 =α22Ecm2∣k∣E\begin{aligned} \frac{d\sigma}{d\Omega} &= \frac{\alpha^2}{4E_{cm}^2}\sqrt{1-\frac{m_{\mu}^2}{E^2}}[(1+\frac{m_{\mu}^2}{E^2})+(1-\frac{m_{\mu}^2}{E^2})\cos^2\theta]\\ &\underset{|\bm{k}|\rightarrow 0}{\longrightarrow} \frac{\alpha^2}{4E_{cm}^2}\frac{|\bm{k}|}{E}\cdot 2\ = \frac{\alpha^2}{2E_{cm}^2}\frac{|\bm{k}|}{E}\\ \end{aligned}

利用初态得到：

vˉ(p′)γμu(p)=−2E(0,1,i,0)\bar{v}(p')\gamma^{\mu}u(p) = -2E(0,1,i,0)

末态为：

u(k)=m(ξξ)v(k′)=m(ξ′−ξ′)u(k) = \sqrt{m}\begin{pmatrix} \xi\\ \xi\\ \end{pmatrix}\quad v(k') = \sqrt{m}\begin{pmatrix} \xi'\\ -\xi'\\ \end{pmatrix}

其中 ξ′\xi' 表示反粒子翻转后的自旋。

得到：

uˉ(k)γμv(k′)=m(ξ†,ξ†)(σˉμ00σμ)(ξ′−ξ′)={0μ=0−2mξ†σiξ′μ=i\begin{aligned} \bar{u}(k)\gamma^{\mu}v(k') &= m(\xi^\dagger,\xi^\dagger)\begin{pmatrix} \bar{\sigma}^{\mu} & 0\\ 0 & \sigma^{\mu}\\ \end{pmatrix}\begin{pmatrix} \xi' \\ -\xi'\\ \end{pmatrix}\\ &= \left\{\begin{aligned} &0\quad & \mu = 0\\ &-2m\xi^\dagger \sigma^i \xi'\quad & \mu = i\\ \end{aligned}\right. \end{aligned}

可得：

M(eR−eL+→μ−μ+)=−2e2ξ†(0100)ξ′(22)\mathcal{M}(e^{-}_{R}e^+_L\rightarrow \mu^-\mu^+) = -2e^2\xi^\dagger\begin{pmatrix} 0 & 1\\ 0 & 0\\ \end{pmatrix}\xi'\tag{22}

这是一个与角度无关的量。对末态可能的自旋求和后得到：

M2=4e2(23)\mathcal{M}^2 = 4e^2 \tag{23}

可以得到微分散射截面为：

dσdΩ(eR−eL+→μ+μ−)=α2Ecm2∣k∣E(24)\frac{d\sigma}{d\Omega}(e_R^-e_L^+ \rightarrow \mu^+\mu^-) = \frac{\alpha^2}{E_{cm}^2} \frac{|\bm{k}|}{E} \tag{24}

束缚态

由于 μ−μ+\mu^{-}\mu^{+} 之间存在库伦相互作用，因此在能量低于阈值时，此仍然可能发生 e−e+→μ−μ+e^{-}e^{+}\rightarrow\mu^{-}\mu^{+} 的反应，并最后生成 μ−μ+\mu^{-}\mu^{+} 的束缚态。我们现在就来处理这样的问题。

对于反应后生成的两个粒子 1,21,2，首先定义以下物理量：

R=12(r1+r2)r=r1−r2K=k1+k2k=12(k1−k2)(25)\begin{aligned} &\bm{R} = \frac{1}{2}(\bm{r}_1+\bm{r}_2)\\ &\bm{r} = \bm{r}_1-\bm{r}_2\\ &\bm{K} = \bm{k}_1 + \bm{k}_2\\ &\bm{k} = \frac{1}{2}(\bm{k}_1-\bm{k}_2) \end{aligned}\tag{25}

反应后生成的束缚态可以用自由态的线性叠加表示。我们考虑反应后的束缚态 M≈2m,K=0M\approx 2m,\bm{K}=0，自旋为 11，方向向上。那么这个束缚态可以表示为：

∣B⟩=2M∫d3k(2π)3ψ~(k)12m12m∣k↑,−k↑⟩(26)\begin{aligned} |B\rangle = \sqrt{2M}\int \frac{d^3k}{(2\pi)^3}\tilde{\psi}(\bm{k})\frac{1}{\sqrt{2m}}\frac{1}{\sqrt{2m}}|\bm{k}\uparrow,-\bm{k}\uparrow\rangle \end{aligned}\tag{26}

其中 ψ~(k)\tilde{\psi}(\bm{k}) 满足：

ψ~(k)=∫d3xeik⋅xψ(r)∫d3k(2π)3∣ψ~(k)∣2=1\begin{aligned} &\tilde{\psi}(\bm{k}) = \int d^3x e^{i\bm{k}\cdot\bm{x}}\psi(\bm{r})\\ &\int \frac{d^3k}{(2\pi)^3}|\tilde{\psi}(\bm{k})|^2 =1\\ \end{aligned}

跃迁到这个束缚态的矩阵元为：

M(↑↑→B)=2M∫d3k(2π)3ψ~(k)12m12mM(↑↑→k↑,−k↑)=2M(−2e2)∫d3k(2π)3ψ~(k)=2M(−2e2)ψ∗(0)(27)\begin{aligned} \mathcal{M}(\uparrow\uparrow\rightarrow B) &= \sqrt{2M}\int \frac{d^3k}{(2\pi)^3}\tilde{\psi}(\bm{k})\frac{1}{\sqrt{2m}}\frac{1}{\sqrt{2m}}\mathcal{M}(\uparrow\uparrow\rightarrow\bm{k}\uparrow,-\bm{k}\uparrow)\\ &= \sqrt{\frac{2}{M}} (-2e^2) \int \frac{d^3k}{(2\pi)^3} \tilde{\psi}(\bm{k})\\ &= \sqrt{\frac{2}{M}}(-2e^2)\psi^*(0)\\ \end{aligned}\tag{27}