晶体X射线衍射
1895 伦琴发现 X射线,对应波长范围为:0.01∼100A∘。其中波长为 0.5∼2.5A∘ 被称为硬 X 射线;波长为 1∼100A∘ 的被称为软X射线。
产生X射线的最简单方法是用加速后的电子撞击金属靶。撞击过程中,电子突然减速,其损失的动能会以光子形式放出,形成X射线光谱的连续部分,称之为轫致辐射。通过加大加速电压,电子携带的能量增大,则有可能将金属原子的内层电子撞出。于是内层形成空穴,外层电子跃迁回内层填补空穴,同时放出波长在0.1纳米左右的光子。由于外层电子跃迁放出的能量是量子化的,所以放出的光子的波长也集中在某些部分,形成了X射线谱中的特征线,此称为特性辐射。
此外,高强度的X射线亦可由同步加速器或自由电子激光产生。同步辐射光源,具有高强度、连续波长、光束准直、极小的光束截面积并具有时间脉波性与偏振性,因而成为科学研究最佳之X射线光源[1]。
Laue 意识到 X射线波长与晶体模型中偶极子阵列量级相近(当时还没有证据表明晶体的微观结构)。Laue 最终照出了 CuSO4 晶体的衍射斑并给出了正确的理论解释。

Fig1:晶体X射线衍射斑[2]
晶体X衍射现象的解释
解释晶体的X射线衍射现象可以分别在实、倒空间进行。
Bragg 公式
在X射线波段,几乎所有物体的折射率 ∼1。如果垂直入射,反射率 ∼0。
假设:
- 光子发生 弹性散射 :ℏω=ℏ′ω′,∣k∣=∣k′∣
- 将晶面当做 镜面:每一平面反射很少一部分(10−3∼10−5)。
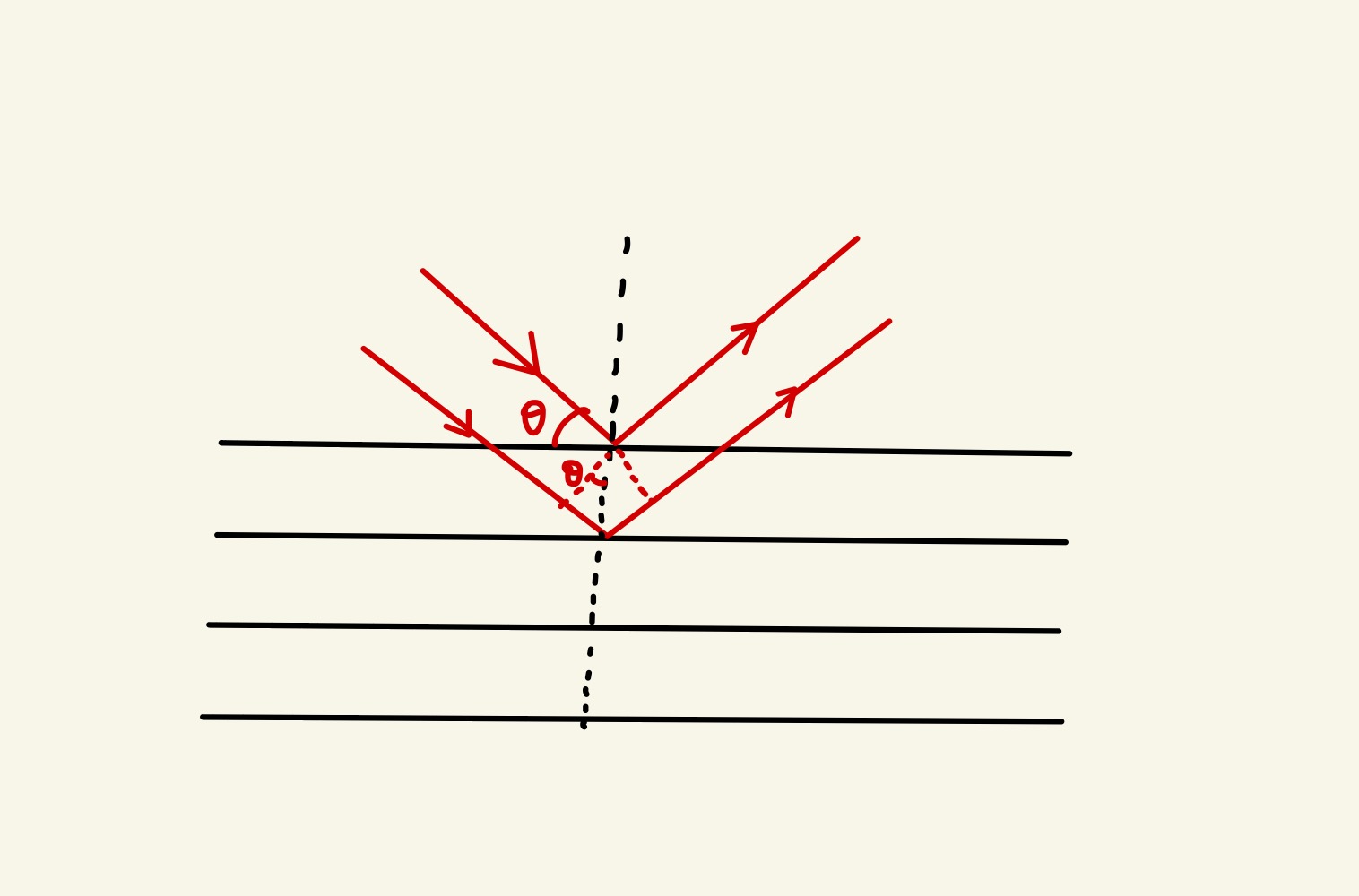
要求多个晶面的反射光干涉加强:
2dsinθ=nλ,n=1,2,3⋯
这就是 Bragg 公式。
容易发现:2d⩾nλ,由此要求实验体系的参数 θ,λ,d 能够匹配,才能观测到衍射斑。
Bragg 公式的原理是很容易理解的,但也存在一些不足之处:
- 镜面假定的物理图像不清楚
- 只能给出衍射角,不能给出光强。
Laue 方程

晶体的X射线衍射主要是X射线与核外电子相互作用的结果。假设散射势正比于电子数密度 V(r)=cn(r)。根据微扰论,初态 ψk 与末态 ψk′ 的跃迁矩阵元为:
μk′k=⟨k′∣V(r)∣k⟩
根据 Born 近似,将初末态看做平面波态:
ψk=eik⋅r;ψk′=eik′⋅r
散射振幅应当正比于跃迁概率,得到:
u=c∫n(r)ei(k−k′)⋅rdr
若取 n(r)=δ(r)
可得:
u=c
所以该比例常数相当于一个点电荷的散射幅。
由周期性条件:
n(r)=n(r+Rl)
可以把电子数密度用倒格矢展开:
n(r)=V1Kh∑n(Kh)eiKh⋅r
可得:
n(Kh)=∫Vdrn(r)e−iKh⋅r
u=cKh∑n(Kh)V1∫drei(k−k′+Kh)⋅r
可以证明,当 V→∞ 时,有:
V1∫drei(k−k′+Kh)⋅r=δk′−k,Kh={1k′−k=Kh0k′−k=Kh
于是得到 Laue 方程
u=cKh∑n(Kh)δk′−k,Kh
可得:
- 衍射加强条件:k′−k=Kn
- 衍射强度:I=u2=c2n2(Kh)
Laue 定理:一组倒点阵矢量 Kh 确定可能的X射线反射、衍射强度比例于电子密度函数的傅里叶系数。
利用 Laue 方程导出 Bragg 公式
考虑到弹性散射条件:
{k′2=k2k′=k+Kh
2k⋅Kh+∣Kh∣2=0
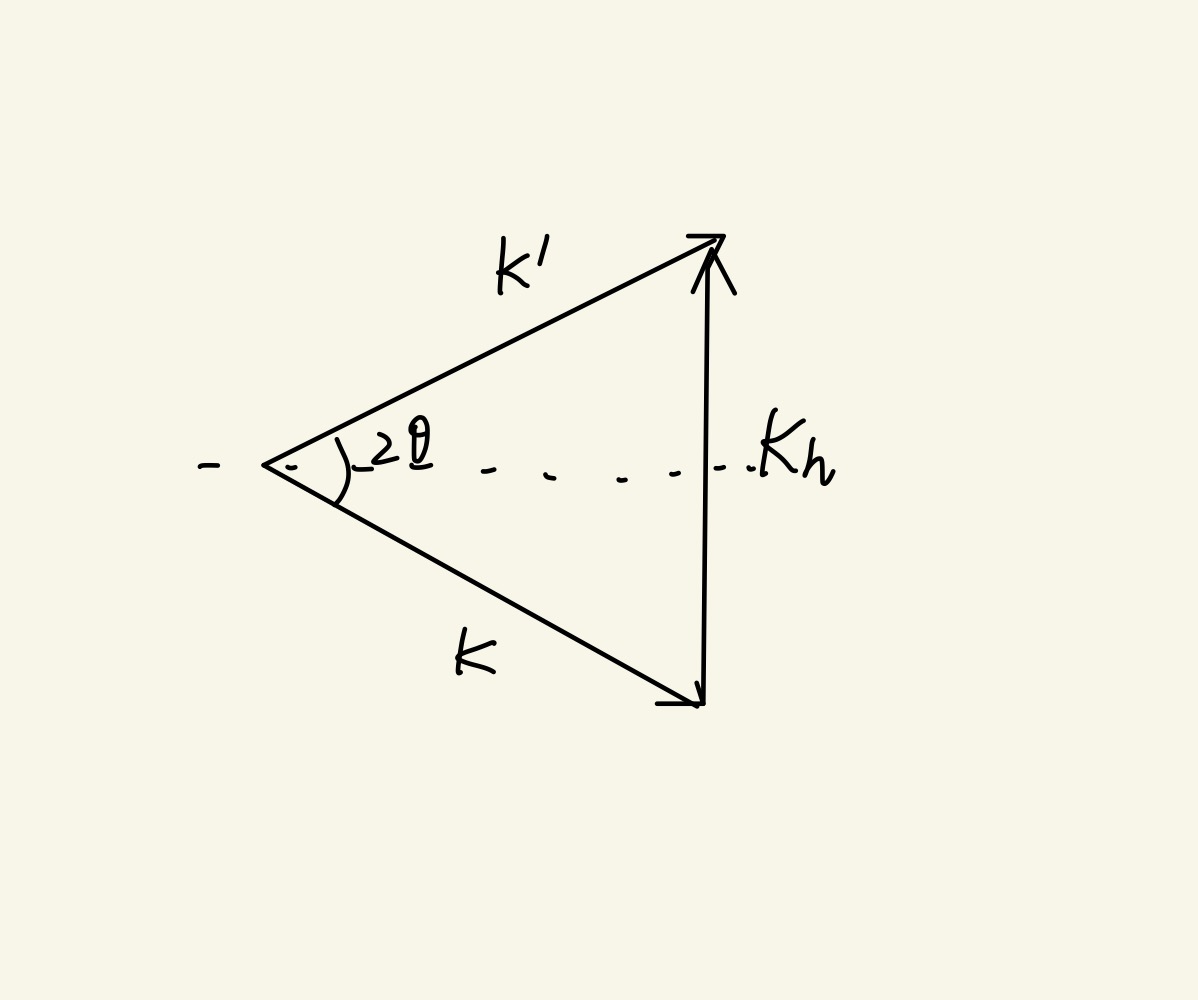
根据几何关系得到:
∣Kh∣2sinθ=∣k∣1
考虑到
∣Kh∣=n∣Kh′∣; d=∣Kh′∣2π; ∣k∣2π=λ
最终导出 Bragg 公式
2dsinθ=nλ
X衍射晶体学分析方法
反射球(厄瓦德球)
以入射波矢为半径在倒空间作球面,球面上的点能够反应衍射波矢。
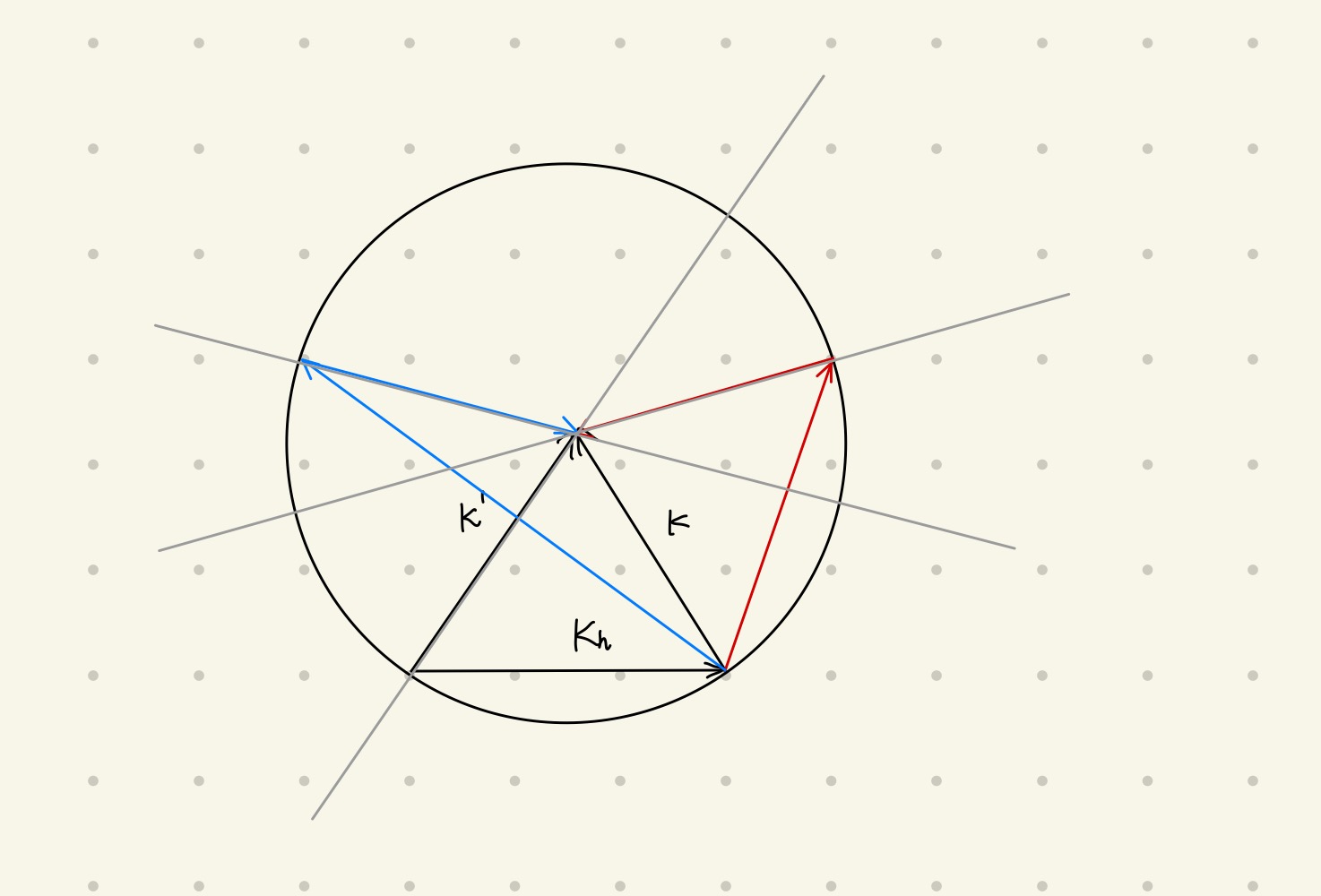
- Laue 法
用连续谱照到固定单晶。
位于最大反射球和最小反射球之间的每个倒格点对应一个衍射波。
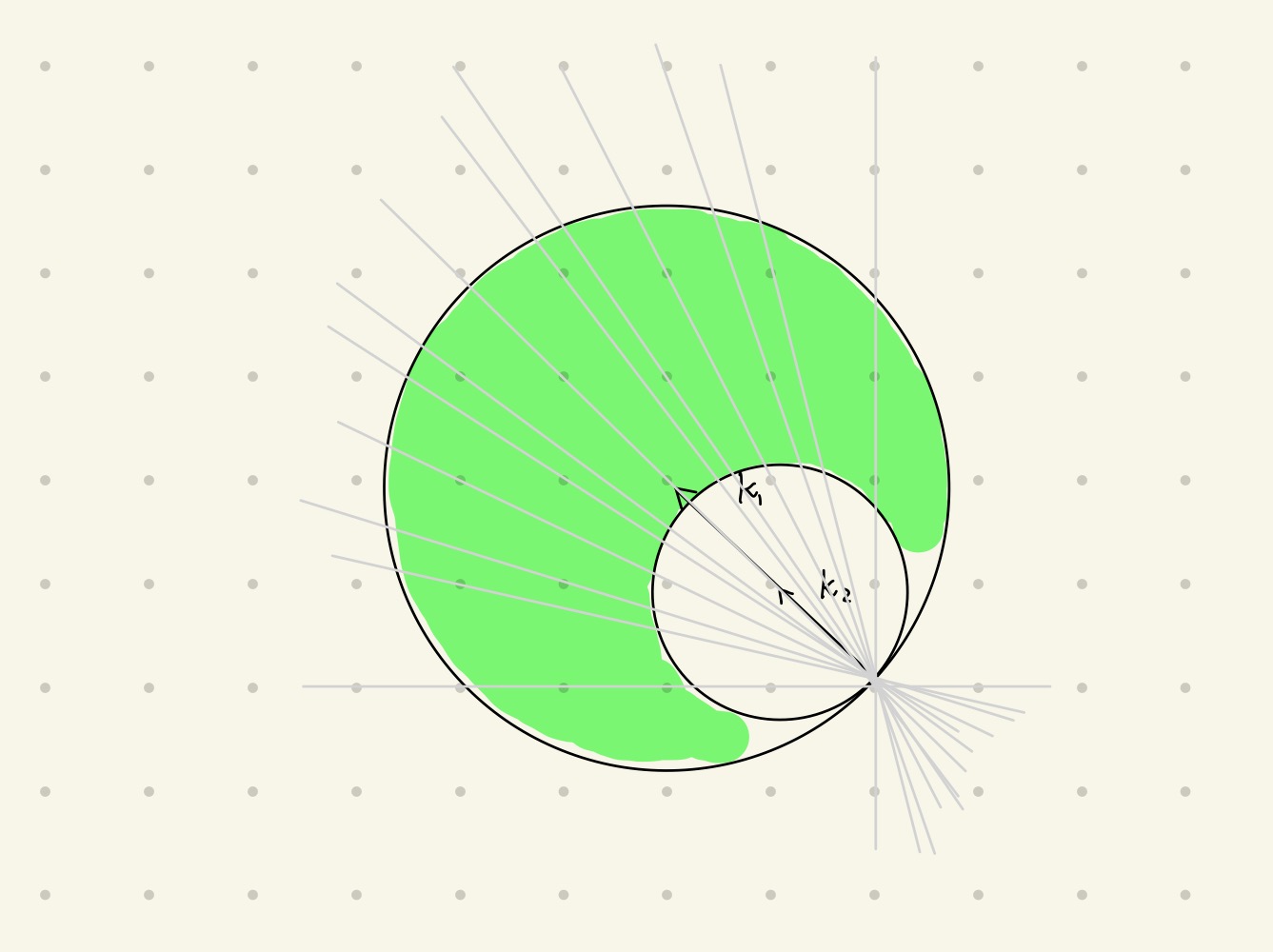
- 转动晶体法
旋转照射单晶。
相当于过固定轴旋转反射球,反射球面掠过倒格点。

- 粉末法
采用平行单色光,使用粉末或多晶样品(比原子尺度仍然大很多)。
大量晶粒的晶轴随机取向,,相当于三维空间中过固定点自由旋转反射球。
形状因子和几何结构因子
现在我们再来考虑 Laue 方程。衍射光强由以下电子数密度的傅里叶变换决定:
n(Kh)=∫Vn(r)e−iKh⋅rdr
这个系数显然与我们所采取的散射模型有关。其中最简单的为:点散射模型:
n(r)=l∑δ(r−Rl)
可得:
n(Kh)=N
u=Kh∑cNδk−k′,Kh
为了考虑电子分布情况的影响,我们引入以下的 形状因子 与 几何结构因子
形状因子
形状因子又称为 原子散射因子。现在我们考虑用 ρ(r−Rl) 来描述节点附近的局域电子密度分布。可得:
n(r)=l∑ρ(r−Rl)
计算傅里叶系数:
n(Kh)=l∑∫drρ(r−Rl)e−iKh⋅r=l∑∫dξρ(ξ)e−i(ξ+Rl)⋅Kh=l∑e−iRl⋅Kh∫dξρ(ξ)e−iξ⋅Kh=l∑e−iRl⋅Khf=Nf
可得:
u=Kh∑cNfδk−k′,Kh
上述中 f 就是原子散射因子:
f=∫dξρ(ξ)e−iξ⋅Kh
原子散射因子代表一个原子内所有电子的散射幅的矢量和与一个电子散射幅之比。
例:氢原子基态电子数密度:
ρ(r)=πa031e−a02r
a0 玻尔半径。
计算原子散射因子:
f=∫drρ(r)exp(−iKh⋅r)=∫0∞∫0π∫02ππa031exp(−a02r−iKhrcosθ)r2sinθdrdθdφ=iKha032∫0∞e−a02r(eiKhr−e−iKhr)rdr=iKha02[(2−iKha0)21−(2+iKha0)21]=(4+Kh2a02)216
几何结构因子
考虑对于复式晶格,基元中不止一个原子,这对应最一般的情况。
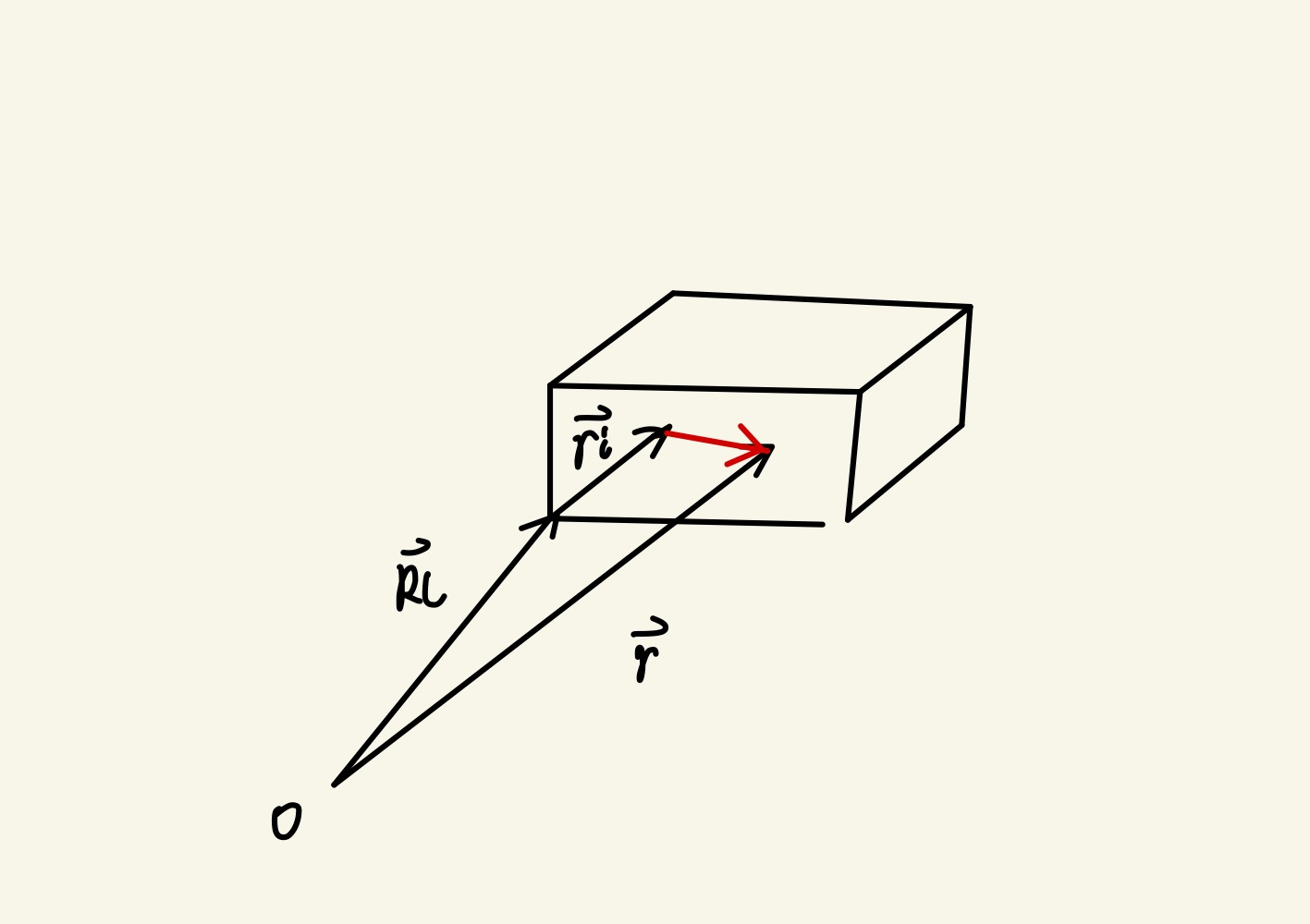
我们用 ρ(r−Rl−ri) 表示第 Rl 个元胞中第 i 个原子的局域电子分布。此时总体的电子数密度分布为:
n(r)=l∑i∑ρi(r−Rl−ri)
计算傅里叶系数:
n(Kh)=l,i∑∫drρi(r−Rl−ri)e−iKh⋅r=l,i∑∫dξρi(ξ)e−i(ξ+Rl+ri)⋅Kh=l,i∑e−i(Rl+ri)⋅Kh∫dξρi(ξ)e−iξ⋅Kh=Ni∑e−iri⋅Khfi=NF(Kh)
F 为几何结构因子
F=i∑fie−iKh⋅ri
衍射光强与几何结构因子的关系:
I∝∣u∣2∝∣F∣2
几何结构因子的物理意义:基元中所有质子的散射幅与一个点电荷散射幅之比。
现在用初基元胞基矢和其倒格矢的展开式代入几何结构因子中,得到:
ri=xi1a1+xi2a2+xi3a3Kh=h1b1+h2b2+h3b3
F(Kh)=i∑fiexp(−2πi(h1xi1+h2xi2+h3xi3))
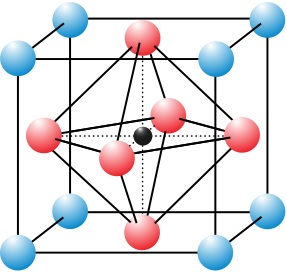
例:CsCl
CsCl 有两个简单立方套构而成。
取 ri:(0,0,0),(21,21,21)
F(h1,h2,h3)=i∑fiexp(−2πi(h1xi1+h2xi2+h3xi3))=fA+fBe−iπ(h1+h2+h3)={fA+fBh1+h2+h3=2nfA−fBh1+h2+h3=2n+1n∈Z
我们发现,当三个面指数相加为奇数时,光强减弱,称为 消光。
上述 消光条件 称为 不完全消光。所谓消光,是指:结构因子能够使空间点阵所允许的某些衍射相互抵消。再来考虑一个例子:
例:Na 晶体
Na 晶体点阵为 bcc结构。我们从两个方面考虑:
-
选取初基元胞进行计算。由于只有一种原子,几何结构因子退化到形状因子。
-
选取单胞进行计算,类比 CsCl,认为 Na 是由两个立方点阵套构而成。我们得到:
F(h,k,l)={2fh+k+l=2n0h+k+l=2n+1n∈Z
我们发现密勒指数和为奇数的倒格点对应的几何结构因子为零,这被称为 完全消光。这些倒格点并不对应衍射。
仔细思考上例中的两种观点,其实它们计算的结果都是正确的。回忆我们在 倒点阵 中所讲述的:若单胞中的结点数不为1,那么选取单胞基矢计算得到的倒点阵会扩大。消光条件正好消去了那些本来并不存在的倒格点。
这件事情需要认真理解,我们再用以下图示说明。下面两组图分别为选取了初基元胞基矢、单胞基矢形成的点阵与倒点阵。注意观察对应倒点阵的元胞大小,由于单胞的体积是初基元胞的两倍,单胞倒格子元胞的体积为初基元胞的一半。根据消光条件,消去淡紫色对应的倒格点,剩余的倒格点与根据初基元胞计算得到的结果一致。
选取初基元胞基矢
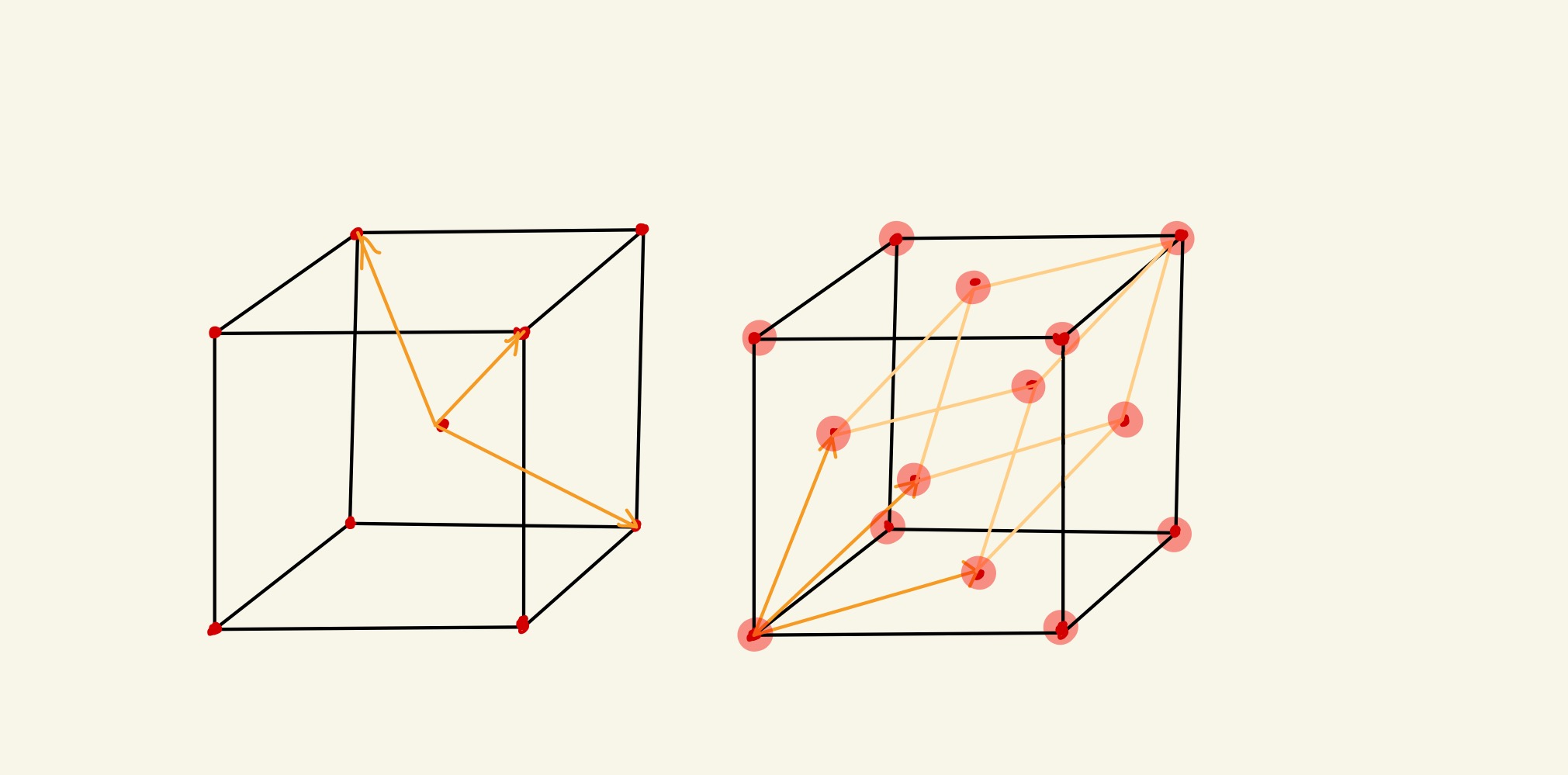
选取单胞基矢
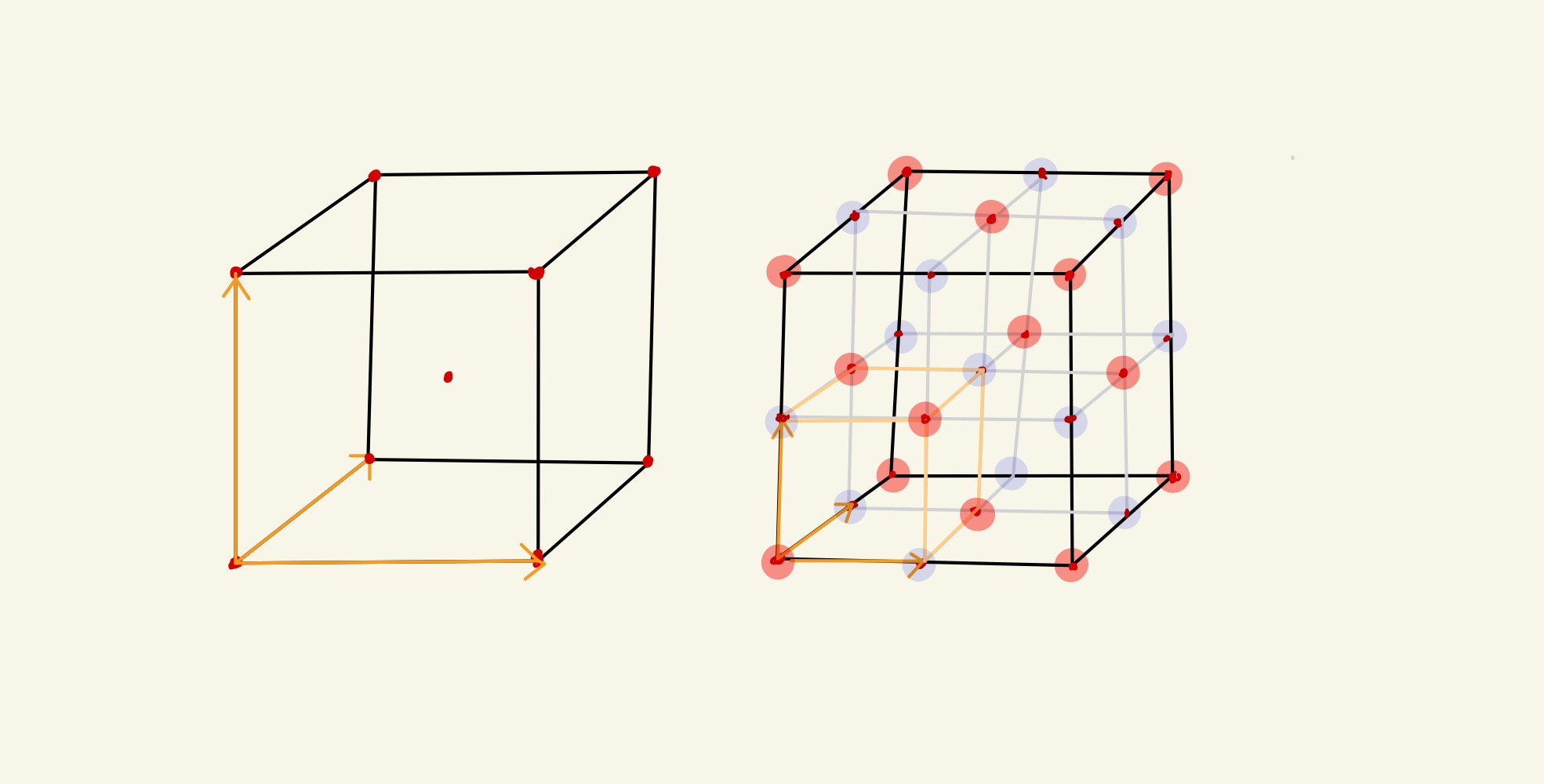
在X射线衍射里习惯使用单胞基矢 a,b,c 建立坐标系。对应的倒格矢为 a∗,b∗,c∗,Laue 方程为:
k′−k=KhklI∝∣F∣2
将由 a,b,c 构成的倒点阵使用消光条件,去掉消光条件对应的格点,得到真实的倒点阵。
a1,a2,a3 坐标系中的衍射条件 ⟺ a,b,c 坐标系中的衍射条件 + 消光条件
参考资料
- 维基百科编者. X射线[G/OL]. 维基百科, 202120210304. https://zh.wikipedia.org/w/index.php?title=X射线&oldid=64608178.
- By Jeff Dahl - Own work, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=3020011
- 胡安,固体物理学