固体物理笔记（四）：晶体结合

晶体结合

晶体中原子的聚集是原子间相互作用的结果，这种使原子发生聚集的强烈的相互作用就是 化学键 $^{[2]}$ 。本篇笔记将会讨论不同类型的键合，如金属键、共价键、离子键、范德瓦耳斯键、氢键等。不同的键合导致了凝聚态物质结构形式的差别（但注意，我们区分不同的键只是为思考的便利，实际上，有很多化学键呈现混合或过渡的特征）。

晶体的内聚力来自于原子核、核外电子之间的静电相互作用。对于两原子系统，我们可以将体系的能量写为：

$E_{tot} = \frac{P_1^2}{2m_1} + \frac{P_2^2}{2m_2} + \frac{q_1q_2}{4\pi\varepsilon_0 R} + E(R)$

其中前三项表示两原子核的动能、原子核之间的静电势能。最后一项为电子的能量。在两原子相互靠近时，不仅会受到核间的库伦斥力，价电子的重新排布也会影响作用力。价电子的重新分布情况取决于原子本身束缚电子的能力，所以，我们以下首先介绍电负性 $^{[1]}$ 。

原子的电负性

电负性（electronegativity，简写EN），也译作离子性、负电性及阴电性，综合考虑了电离能和电子亲合能，首先由莱纳斯·鲍林于1932年提出 $^{[3]}$ 。

以下分别介绍电离能与亲和能。

电离能
电离能（Ionization energy），常简记为 $E_I$ 。指的是将一个电子自一个孤立的原子、离子或分子移至无限远处所需的能量。更广义的用法，第一电离能定义为气态原子失去一个电子成为一价气态正离子所需的最低能量，记作 $I_1$ ；气态一价正离子失去一个电子成为气态二价正离子所需的能量称为第二电离能，记作 $I_2$ 。依此类推 $^{[4]}$ 。

Fig:第一电离能的周期性变化 $^{[5]}$

电离能衡量一个原子对价电子束缚能量的强弱。

亲和能
电子亲合能（electron affinity， $E_{ea}$ ）的定义是，将使一个电子脱离一个气态的离子或分子所需耗费（释放）的能量。亲和能衡量一个原子束缚外来电子的能力 $^{[6]}$ 。

电负性综合了电离能与亲和能，Mulliken 建议采用：

$\chi = \frac{1}{2eV}(|E| + |I_1|)$

我们常常做一定的线性变换，取用最后得到的相对值。这个相对大小表示元素原子在分子中对成键电子的吸引能力。元素电负性数值越大，原子在形成化学键时对成键电子的吸引力越强。

Pauling，Allred、Rochow 也提出了标度电负性的方法。比较电负性时，注意使用的标度要相同。以下为Pauling标度。
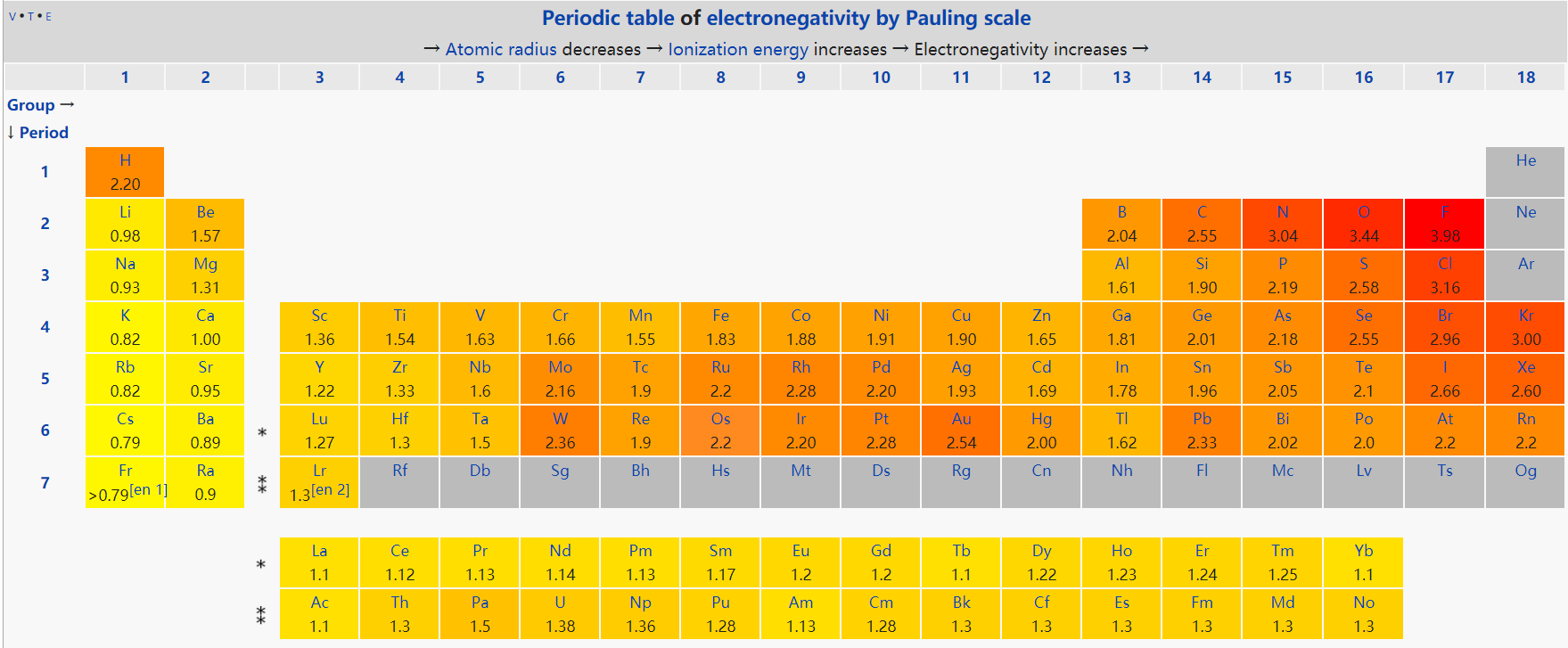
电负性的周期性变化，Pauling

Fig:电负性的周期性变化，Pauling $^{[7]}$

电负性的周期性变化规律为：

在一个周期内电负性由左向右不断增强。
周期表由上到下电负性逐渐减弱。
周期表越往下，一个周期内的电负性差别越小。

晶体结合的类型

介绍完电负性的概念之后，谈论晶体结合的分类是容易理解的。

金属结合

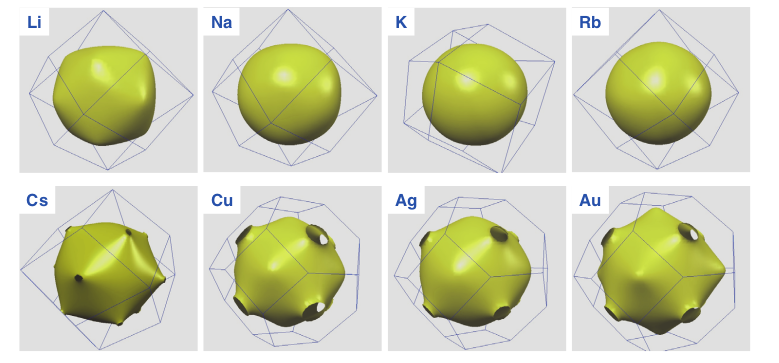
金属分为碱金属、过渡金属、贵金属。这类元素的电负性通常较小，对价电子的束缚能力很弱，在金属晶体中，价电子呈现出 退局域化 的特征，价电子为整个金属晶体所共有。价电子的公有化将使得电子的能量减小，这也是吸引力的来源。这种键合方式称为 金属键。

Fig: 金属键示例 $^{[8]}$

以一个简单例子来理解退局域化使得电子能量降低：

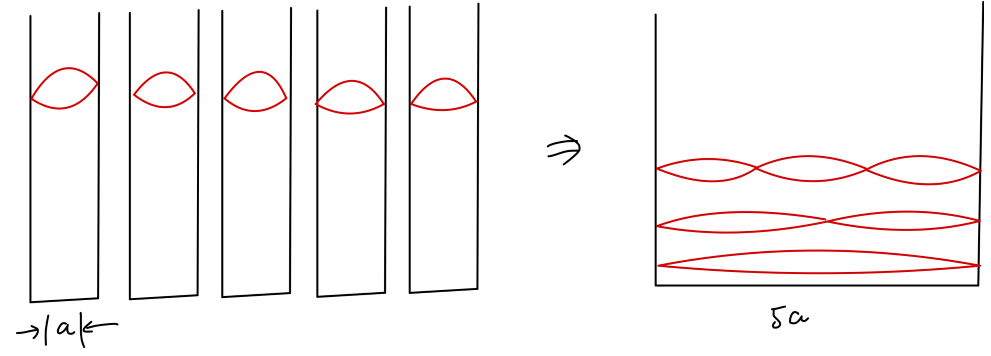
假设退局域化前，五个电子分别被限制在五个宽度为 $a$ 的无穷势阱中，那么得到基态能量为：

$E = \frac{5\hbar^2\pi^2}{2ma^2}$

退局域化之后，五个电子被限制在一个宽度为 $5a$ 的无穷势阱中，考虑到泡利不相容原理，基态能量为：

$E' = \frac{\hbar^2\pi^2}{2m(5a)^2}(2+2\cdot 4 + 9) = \frac{19\hbar^2\pi^2}{50ma^2} < E$

通过这样一个简单模型的计算，我们得到了认识——退局域化确实能够使得电子能量降低。

金属结合的特点
无方向性

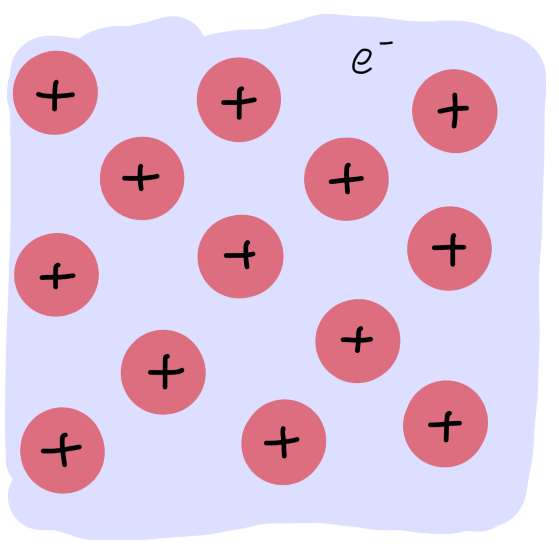
Fig: 凝胶模型

金属晶体的排斥力来自于费米能：

$E_F = \frac{\hbar^2}{2m}(3\pi^2 n_0)^{2/3}$

$n_0$ 电子数密度。体积越小，电子云密度越大，系统的动能增加，同时正离子间的排斥也增大，表现出排斥作用。

金属结合是一种体积效应，对原子排列并无特殊要求，很多金属晶体采取密堆结构(fcc，hcp)，配位数为12；体心立方结构(bcc)也是一种常见的结构，配位数为8。

金属的很多特性，如高导电性、高导热性、范性（延展性）、金属光泽都与金属结合的电子公有化具有密切关系。

共价结合

电负性较强（ $\mathrm{IVA}\sim \mathrm{VIIA}$ ）的元素，结合成晶体时，多采用共价结合。

首先介绍共价键。

共价键

当中性原子依靠共价电子结合时，必须从每个原子中取一个电子成键，现在我们考虑最简单的例子——氢分子。海特勒（Heitler），伦敦（London）近似求了氢分子的基态能量。

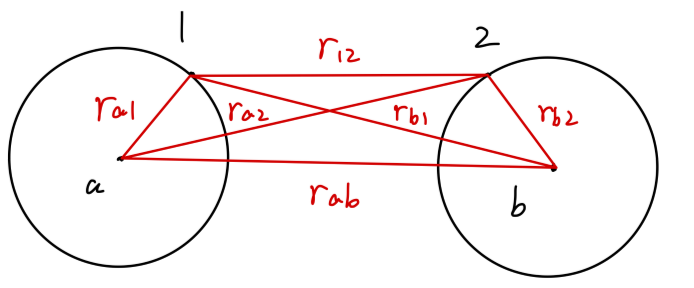
体系的哈密顿量为：

$\hat{H} = -\frac{\hbar^2}{2m}(\nabla_1^2+\nabla_2^2) -\frac{e^2}{r_{a1}}-\frac{e^2}{r_{a2}}-\frac{e^2}{r_{b1}}-\frac{e^2}{r_{b2}}+\frac{e^2}{r_{12}}+\frac{e^2}{r_{ab}}$

求解这个方程是非常困难（现在还没求出解析解，只有一些近似求出数值解的方法）。总之我们若得到了本征波函数 $\Phi$ ，就可以得到体系能量：

$E(R_{ab}) = \int \Phi^* \hat{H} \Phi d\bm{r}$

考虑这个波函数的轨道部分，有两种情况：轨道部分对称对应自单态；轨道部分反对称对应自旋三重态。

$\begin{aligned} \Phi_S &= \frac{1}{\sqrt{2}} [\varphi_{a}^{(1)}\varphi_{b}^{(2)} + \varphi_{a}^{(2)}\varphi_{b}^{(1)}]\\ \Phi_A &= \frac{1}{\sqrt{2}} [\varphi_{a}^{(1)}\varphi_{b}^{(2)} - \varphi_{a}^{(2)}\varphi_{b}^{(1)}]\\ \end{aligned}$

将上述波函数代入，计算对应的能量，可以得到：

$E_S = K+J,E_A = K-J$

其中：

$\begin{aligned} K &=\langle \varphi_a^{(1)}\varphi_b^{(2)}|\hat{H}| \varphi_a^{(1)}\varphi_b^{(2)}\rangle \\ J &= \mathrm{Re}(\langle \varphi_a^{(1)}\varphi_b^{(2)}|\hat{H}| \varphi_a^{(2)}\varphi_b^{(1)}\rangle) \\ \end{aligned}$

上式中 $K$ 表示两个原子间的库伦相互作用能， $J$ 为交换能，对于氢分子情况， $J<0$ 。由此，单态能量较低，对应成键态，能构成稳定分子；三重态能量较高，对应反键态，不能构成稳定分子。形成共价键后，这两个电子由两个原子共享，且成 反平行排列。

Fig: 氢分子 $^{[9]}$

共价键的特点：

饱和性
一个原子只能形成一定数目的共价键，这决定于未成对电子的数目。
方向性
成键方向取决于形成共价键的两个电子轨道的相互重叠程度。

杂化理论

在金刚石中，每一个 $\mathrm{C}$ 原子和周围的4个 $\mathrm{C}$ 原子形成共价键。基态碳原子的电子组态为： $1s^22s^22p^2$ 。只有2个未成对电子，为何会形成四根共价键呢？

Pauling 以量子力学为基础提出了杂化轨道理论。其核心思想是将不同原子轨道的叠加重组，从而成为数目相同，能量相等的新轨道。对于金刚石中的 $\mathrm{C}$ 原子来说，经历了如下过程：

从基态 $1s^22s^22p^{2}$ $\rightarrow$ 激发态 $1s^22s^12p^{3}$ 需要能量 $4\mathrm{eV}$ 。

这样就产生了四个未配对电子，其中3个在 $2p$ 轨道上，1个在 $2s$ 轨道上，这四个轨道叠加形成一个4个等价的 $sp^3$ 杂化轨道。

成键放出能量 $7.6\mathrm{eV}$ 。因此，净释放能量 $\Delta E=3.6\mathrm{eV}$ 。

我们发现这种成键方式确实使得体系能量降低了。

这四个 $sp^3$ 轨道为：

$\begin{aligned} \Psi_1 = \frac{1}{2}(\varphi_{2s}+\varphi_{2p_x}+\varphi_{2p_y}+\varphi_{2p_z})& \quad [111]\\ \Psi_2 = \frac{1}{2}(\varphi_{2s}+\varphi_{2p_x}-\varphi_{2p_y}-\varphi_{2p_z})& \quad [1\bar{1}\bar{1}]\\ \Psi_3 = \frac{1}{2}(\varphi_{2s}-\varphi_{2p_x}+\varphi_{2p_y}-\varphi_{2p_z})& \quad [\bar{1}1\bar{1}]\\ \Psi_4 = \frac{1}{2}(\varphi_{2s}-\varphi_{2p_x}-\varphi_{2p_y}+\varphi_{2p_z})& \quad [\bar{1}\bar{1}1]\\ \end{aligned}$

这四个 $sp^3$ 轨道的夹角为 $109.5\degree$ 。

Fig: $sp^3$ 杂化 $^{[10]}$

$\mathrm{C},\mathrm{Si},\mathrm{Ge}$ 晶体均采用 $sp^3$ 杂化。其配位数为4，一个中心原子与周围4个原子形成一个四面体。

除了 $sp^3$ 杂化之外，还有 $sp,sp^2, sp^3d$ 等杂化方式，此处不做介绍。

共价键的极性

上述介绍的金刚石和氢分子，形成共价键的原子相同，自然电负性一样，两原子对成键电子对的吸引能力相同，可以预期共价键的正电中心与负电中心重合，我们称这种共价键为 非极性共价键。对应若形成共价键的两原子的电负性不同，如 $\mathrm{HCl}$ 分子， $\mathrm{Cl}$ 对电子的吸引力更强，所以成键电子对向 $\mathrm{Cl}$ 偏移，此时共价键的正、负电荷中心并不重合，我们称这种为 极性共价键。

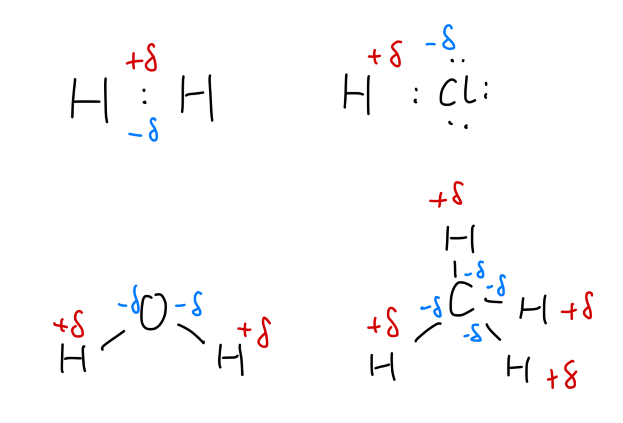
Fig：共价键的极性&分子的极性

我们要把分子的极性与共价键的极性区分开来，分子的极性取决与整体的正、负电荷中心是否重合。非极性共价键构成的分子一定是非极性分子；极性共价键可以形成极性分子，如 $\mathrm{H_2O}$ ，也可以形成非极性分子，如 $\mathrm{CH_4}$ 。

原子晶体

内部原子以共价键的形式连的晶体为 原子晶体。典型的物质有：金刚石、硅、二氧化硅、碳化硅等。特点是熔沸点很高，硬度大。

离子结合

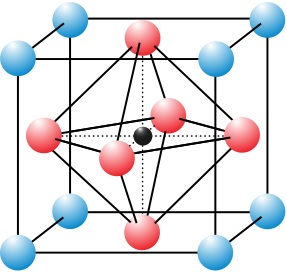
当两个电负性相差很大的元素，例如 $\mathrm{IA}:\mathrm{Li},\mathrm{Na}$ 与 $\mathrm{VIIA}:\mathrm{F},\mathrm{Cl}$ 结合时，电负性强的元素会完全夺走成键电子对，形成负离子；失去电子的元素成为正离子。其以离子而不是以原子为结合单元。在离子晶体中，正负离子交替排列。

Fig：NaCl晶体，其中绿色代表 $Cl^{-}$ ，其中紫色代表 $Na^{+}$ $^{[11]}$

随着成键原子相差电负性的增加，成键也发生变化：
共价键 $\rightarrow$ 极性共价键 $\rightarrow$ 离子键
需要指出，这种过渡并没有严格的界限。

范德瓦尔斯结合

上述提到的金属键、共价键、离子键都是很强的键，其平均每个原子的结合能大约为几个电子伏特的量级。除此之外，我们发现具有满壳层电子结构的惰性气体原子在形成晶体时，电子结构基本不变，但原子之间也存在一种很弱的相互作用力。称为 范德瓦尔斯 力。

电子的零点运动会产生一个瞬时的电偶极矩，典型的由此下列两种情况：

电偶极矩同向。原子相互吸引。
电偶极矩反向。原子相互排斥。

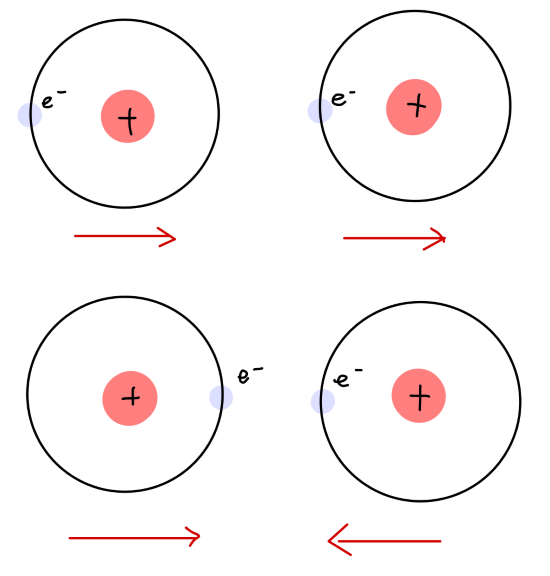
从统计意义上来说，发生情况1的概率要大于2的概率，因此吸引力占优势，这种吸引力就是范德瓦尔斯力。

现在使用一个简化的模型去理解这件事
考虑无耦合时的哈密顿量为：

$H_0 = \frac{1}{2m}p_1^2 + \frac{1}{2}cx_1^2 + \frac{1}{2m}p_2^2 + \frac{1}{2}cx_2^2$

特征频率：

$\omega_0 =\sqrt{\frac{c}{m}}$

耦合的哈密顿量：

$H_1 \approx -\frac{2e^2x_1x_2}{R^3}$

引入简正坐标：

$x_a = \frac{1}{\sqrt{2}}(x_1 + x_2),\quad x_a = \frac{1}{\sqrt{2}}(x_1-x_2)$

可得

$H = [\frac{1}{2m}p_s^2 + \frac{1}{2}(c-\frac{2e^2}{R^3}) x_s^2] + [\frac{1}{2m}p_a^2 + \frac{1}{2}(c+\frac{2e^2}{R^3}) x_a^2]$

耦合系统的特征频率为：

$\omega = \sqrt{\frac{C\pm \frac{2e^2}{R^3}}{m}}$

系统零点能：

$\begin{aligned} \Delta E(R) &= \frac{1}{2}\hbar(\omega_s+\omega_a)-\hbar\omega\\ &=-\hbar\omega \frac{1}{4}(\frac{2e^2}{cR^3})^2= -\frac{A}{R^6} \end{aligned}$

由此得到的正比于 $R^{-6}$ 的吸引势就是范德瓦尔斯力的来源。并且，我们看到该项中出现了普朗克常数，从这个意义上来说，范德瓦尔斯力是一种量子效应。

范德瓦尔斯键是一种弱键，无方向性，无饱和性。惰性原子晶体的结构类似于金属，多采取密堆积结构，除了 $\mathrm{He^3},\mathrm{He^4}$ 外，全部采取 fcc 结构。

氢键

$\mathrm{H}$ 属于 $\mathrm{IA}$ 族元素，但与其他 $\mathrm{IA}$ 族元素，如锂、钠等相比，电离能要大很多。因此，氢原子难以形成离子键。

元素	第一电离能
氢	$13.6 \mathrm{eV}$
锂	$5.39 \mathrm{eV}$
钠	$5.14 \mathrm{eV}$

在一定条件下，氢原子可以与一个电负性很强的原子形成极性共价键的同时，再与另一个电负性很强（例如 $\mathrm{O,F,N}$ ）的原子形成氢键。

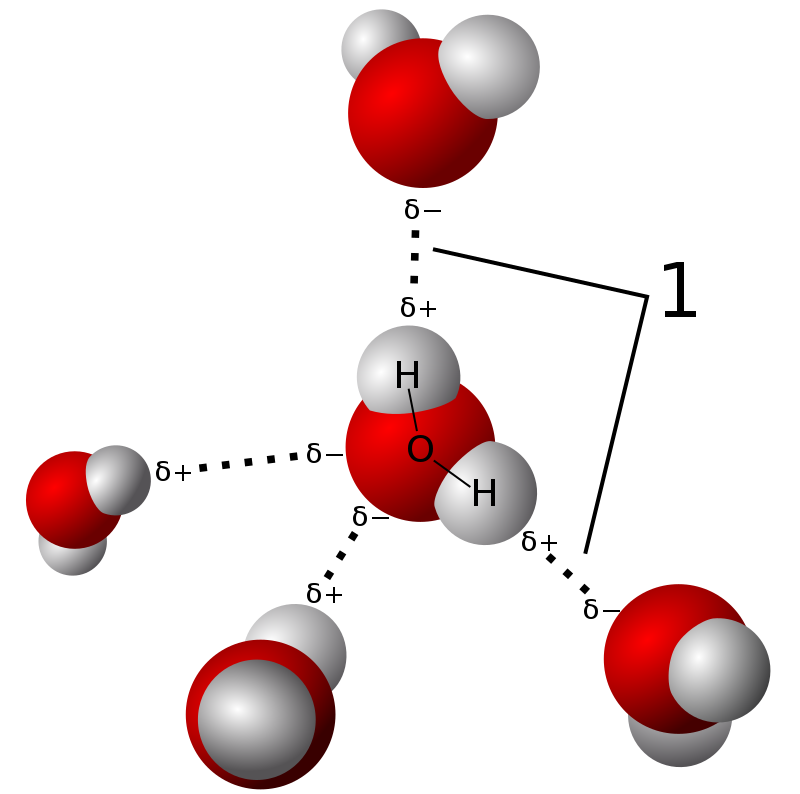
Fig：冰中水分子间的氢键

一个典型的例子是水。氧的价电子组态为 $2s^22p^4$ ，水分子中的氧原子是 $sp^3$ 杂化，形成 4 个 $sp^3$ 杂化轨道。其中两个轨道上各有一个未成对电子，另外两个轨道上各有一对电子。其中未成对电子与氢原子形成共价键，这个共价键的极性很强。正电中心向氢原子偏移，近乎裸露的质子对相邻氧原子的孤对电子有吸引力，形成了氢键，键能约为 $0.1\mathrm{eV}$ 。

氢键具有饱和性与方向性。在冰以及很多有机分子材料中起重要的作用。

混合键

有很所分子或晶体的键合不单纯的属于上述五种键合方式，而是综合性的。我们以石墨为例进行介绍。

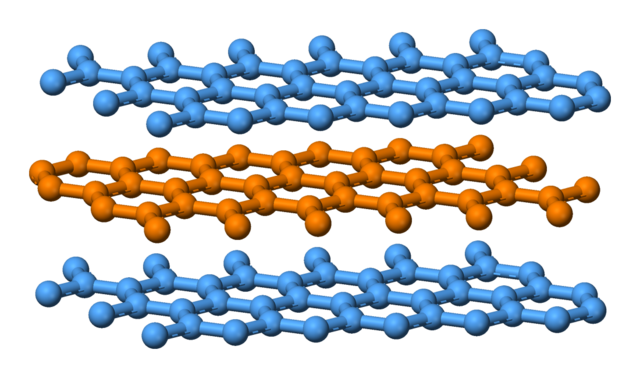
Fig：石墨的结构 $^{[12]}$

石墨中的 $\mathrm{C}$ 原子电子组态为 $1s^22s^22p^2$ ，采取 $sp^2$ 杂化，得到 $3$ 个 $sp^2$ 杂化轨道与 $1$ 个 $2p_z$ 轨道。三个杂化轨道共面，一个 $\mathrm{C}$ 原子与平面内三个相邻的 $\mathrm{C}$ 原子分别形成共价键。每层 $\mathrm{C}$ 原子多余的 $2p_z$ 电子，其轨道垂直于杂化轨道形成的平面，这些电子退局域化，形成金属键。层与层之间靠范德瓦尔斯键，结合成三维石墨晶体。

石墨晶体这种复杂的键合方式可以解释其许多性质：在平面内具有良好导电性；层与层之间的作用弱，具有润滑性。

$sp^2$ 轨道杂化

Fig： $sp^2$ 杂化 $^{[13]}$

$\mathrm{C}$ 基态 $1s^22s^22p^2\rightarrow 1s^22s^12p^3$

$\begin{aligned} \Psi_1 &= \frac{1}{\sqrt{3}}(\varphi_{2s}+\sqrt{2}\varphi_{2p_x})\\ \Psi_2 &= \frac{1}{\sqrt{3}}\varphi_{2s}+\frac{1}{\sqrt{2}}\varphi_{2p_y}-\frac{1}{\sqrt{6}}\varphi_{2p_x}\\ \Psi_3 &= \frac{1}{\sqrt{3}}\varphi_{2s}-\frac{1}{\sqrt{2}}\varphi_{2p_y}-\frac{1}{\sqrt{6}}\varphi_{2p_x}\\ \end{aligned}$

结合能

严格的从薛定谔方程出发求解，求解薛定谔方程是一件很困难的事情。我们在这里期望用唯象方法去对晶体的结合能做一些讨论。

我们考虑内能函数与宏观可观测量之间的关系。根据热力学第一定律：

$dU = TdS - pdV$

在零温时，有：

$dU = -pdV$

可得

$\frac{dU}{dV}|_{V_0} = -p\approx 0$

考虑到外压强 $p$ 与晶体的内压强相比是很小的，所以在上式中近似有 $p\approx 0$ 。 $V_0$ 为平衡体积。
计算晶体的体积弹性模量模量

$\kappa = -\frac{dp}{(dV/V)} = V \frac{d^2 U}{dV^2}$

如果我们能够给出一个晶体内能的表达式，那么通过实验测量平衡体积与弹性模量，就可以确定表达式中的待定参数，这是该唯象理论的研究思路。

下面以离子晶体、惰性气体为例进行说明。

离子晶体的结合能

静电吸引势
离子晶体由交错排列的正负离子构成。以 $\mathrm{NaCl}$ 晶体为例，设原点有一个正离子，正负离子间距为 $r$ ，任意一离子距离原点的距离为：

$d = \sqrt{n_1^2+n_2^2+n_3^2}$

其中 $n_1,n_2,n_3\in \mathbb{N}$ ， $n_1+n_2+n_3$ 为奇数代表负离子，为偶数代表正离子。

这个正离子的库伦能为：

$\frac{1}{2}\sum_{n_1n_2n_3} \frac{(-1)^{n_1+n_2+n_3}e^2}{\sqrt{n_1^2+n_2^2+n_3^2}r}$

一对离子的平均库伦能：

$\frac{e^2}{4\pi\varepsilon_0 r}\sum_{n_1n_2n_3} \frac{(-1)^{n_1+n_2+n_3}}{\sqrt{n_1^2+n_2^2+n_3^2}} = -\frac{\alpha e^2}{4\pi\varepsilon_0 r}$

$\alpha$ 为 Madelung 常数，与晶体结构有关，总是一个正数：

$\alpha = -\sum_{n_1n_2n_3} \frac{(-1)^{n_1+n_2+n_3}}{\sqrt{n_1^2+n_2^2+n_3^2}}$

离子晶体中的静电吸引势也被称作 Madelung 能。

对于不同的晶体结构，可得到 Madelung 常数的值：

晶体结构	Madelung 常数
$\mathrm{NaCl}$	$1.7476$
$\mathrm{CsCl}$	$1.7627$
$\mathrm{ZnS}$	$1.6381$

关于 Madelung 常数的数值计算，我们可以将单胞取为中性单元，这样上述的级数收敛是很快的。

重叠排斥能
离子的晶体的排斥能起因于满壳层离子之间电子云的重叠。排斥力是一种短程力，我们考虑其形式为：

$\frac{b}{r^n}$

对于 $\mathrm{NaCl}$ 晶体来说，每个离子的配位数为6，由此每对离子的平均排斥能为：

$\frac{6b}{r^n}$

离子晶体结合能
考虑上述Madelung能与重叠排斥能，晶体的内能可以写为：

$U = N[-\frac{\alpha e^2}{4\pi \varepsilon_0 r} + \frac{6b}{r^n}] = N[-\frac{A}{r} + \frac{B}{r^n}]$

晶体的总体积与粒子数存在以下关系：

$V = N\cdot 2r^3$

考虑晶体的平衡体积为 $V_0$ ，可以得到：

$\begin{aligned} \frac{d U}{d V}|_{V_0} = \frac{1}{6r_0^2}[\frac{A}{r_0^2} - \frac{nB}{r_0^{n+1}}]=0 \end{aligned}$

体积弹变模量可以写为：

$\kappa = V(\frac{d^2 U}{d V^2})|_{V_0} = \frac{(n-1)\alpha e^2}{(4\pi\varepsilon_0)18r_0^4}$

可以得到晶体的结合能

$W = \frac{N\alpha e^2}{4\pi\varepsilon_0r_0}(1-\frac{1}{n})$

通常 $n \approx 8\sim10$

对弹性模量与结合能的计算，我们发现：

结合能主要取决于吸引势。
体积弹性模量主要来自于排斥力。

惰性气体晶体的结合能

考虑惰性气体的内能。主要为两部分组成：

吸引势为范德瓦尔斯势，与原子间距的六次方成反比。
排斥势为原子间距足够近时电子云的交叠导致的泡利排斥势。

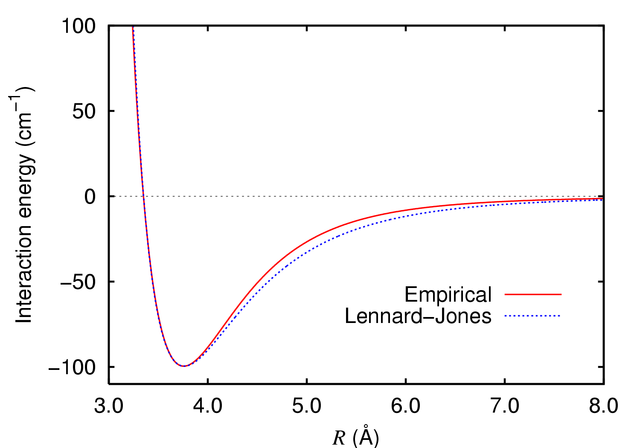
Fig：Lennard-Jones 势 $^{[14]}$

我们经验性的给出一个与原子间距十二次方成反比的排斥势能（这个是一个近似的公式），由此给出的势能为 Lennard-Jones 势：

$\begin{aligned} U(R)&=-\frac{A}{R^6} + \frac{B}{R^{12}}\\ &= 4\epsilon [(\frac{\sigma}{R})^{12} - (\frac{\sigma}{R})^6] \end{aligned}$

上式最后进行了变量替换，替换后参量的物理意义更加清晰：

$\sigma$ 为势能为零时的原子间距。

$\epsilon$ 为势阱深度。
具体来说，我们可以计算 Lennard-Jones 势的极小值：

$\frac{dU}{dR}|_{R_0} = -\frac{4\epsilon}{R_0}[12(\frac{\sigma}{R_0})^{12} - 6(\frac{\sigma}{R_0})^6)]=0\Rightarrow R_0 = 2^{1/6} \sigma$

由此：

$U(R_0) = -\epsilon$

计算总内能（惰性气体晶体多为fcc结构，此处取fcc结构进行计算）：

$\begin{aligned} U_{tot} &= \frac{1}{2}4\epsilon \sum_{j} [(\frac{\sigma}{p_{ij}R})^{12} - (\frac{\sigma}{p_{ij}R})^6]\\ &=2\epsilon [ A_{12}(\frac{\sigma}{R})^{12} - A_6(\frac{\sigma}{R})^6] \end{aligned}$