固体物理笔记（十）：费米统计与电子比热

费米统计与电子比热

基态的费米分布函数和费米能

一般的金属问题往往主要只涉及导带中的电子。因此，下面的讨论只考虑导带中的电子。导带中的电子可以看作 自由费米气体，即：自由的、无相互作用的、遵从泡利不相容原理的电子气。

这样的一个使用单电子近似描述的系统的宏观态可以用电子在这些本征态间的统计分布来描述。对于系统的平衡态，费米统计的基本原理可以归结为一个完全确定的 费米统计分布函数。

$f(E) = \frac{1}{1 + e^{(E - E_F)/k_BT}} \tag{1}$

$E_F$ 为化学势，对于费米子系统来说，称为 费米能。

所有态上分布的总粒子数当然等于 $N$ ，即：

$\int_{0}^{\infty} f(E)N(E)dE = N \tag{2}$

当 $E = E_F$ 时，得到：

$f(E_F) = \frac{1}{2}$

考虑基态 $(T=0K)$ 的分布函数和费米能 $E_F^0$ 。由 $(1)$ 可得：在零温度时，所有 $E < E_F^0$ 的本征态都将被完全填满，所有 $E > E_F^0$ 的本征态都是空缺的。 $E_F^0$ 为零温时的费米能。分布函数成为一个阶跃函数。

$f^0(E) = H(E_F^0-E) \tag{3}$

我们使用上标 $0$ 来表示零温。

此时下列关系成立：

$-\frac{\partial f^0}{\partial E} = \delta(E-E_F^0) \tag{4}$

对于自由电子气，有：

$\frac{\hbar^2}{2m}{k_F^{0}}^{2} = E_F^0 \tag{5}$

我们称 $E = E_F^0$ 的等能面为 费米面。在零温时，费米面就是电子填充能态的边界。

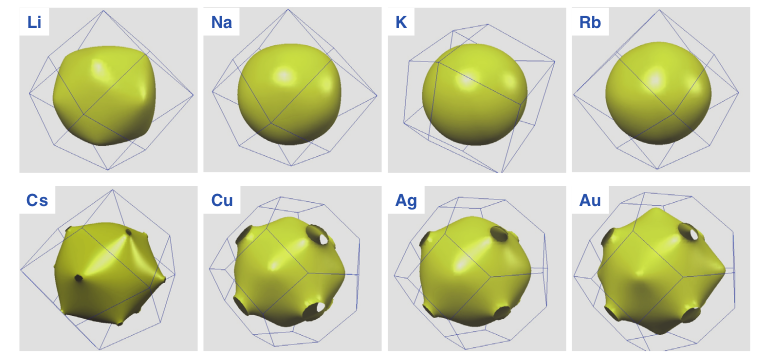
Fig：碱金属的费米面

根据 $(2)$ 式得到：

$\begin{aligned} \int_{0}^{\infty}f^0(E)N(E)dE = \int_{0}^{E_F^0} \frac{2V}{(2\pi)^2}(\frac{2m}{\hbar})^{3/2}E^{1/2}dE =N \end{aligned}$

可以从中得到费米能为：

$\begin{aligned} E_F^0 &= \frac{\hbar^2}{2m}(\frac{3\pi^2 N}{V})^{2/3}\\ & = \frac{\hbar^2}{2m} (3\pi^2n_0)^{2/3},\quad n_0 = \frac{N}{V}\\ \end{aligned} \tag{6}$

对于一般的金属来说

$\begin{aligned} &E_F^0 \sim 1.5\sim 7 \mathrm{eV}\\ &k_F^0 \sim 10^8 \mathrm{cm}^{-1}\\ \end{aligned}$

在绝对零度下，晶格的动量为零。如此电子的准动量与真实动量相等。

$mv_F = \hbar k_F^0 \tag{7}$

基态能量：

$\begin{aligned} U_0 &= \int_{0}^{\infty} E f^0(E) N(E)dE \\ &= \int_{0}^{E_F} \frac{V}{2\pi^2}(\frac{2m}{\hbar^2})^{3/2} E^{3/2} dE\\ &= \frac{2}{5}\frac{V}{2\pi^2}(\frac{2m}{\hbar^2}) {E_{F}^{0}}^{5/2}\\ & = \frac{3}{5}NE_F^0 \end{aligned}$

每个电子的平均能量为：

$\frac{U_0}{N} = \frac{3}{5}E_F^0 \tag{8}$

体弹模量：

$\begin{aligned} B &= \frac{1}{\kappa} = -V \frac{\partial p}{\partial V} = V^2 \frac{\partial^2 U_0}{\partial V^2}\\ & = \frac{2}{3}n_0E_F^0\\ \end{aligned} \tag{9}$

注意以上计算得到的体弹模量和实验测量值具有较大差距：因为没有考虑势能项。

激发态的分布函数和费米能

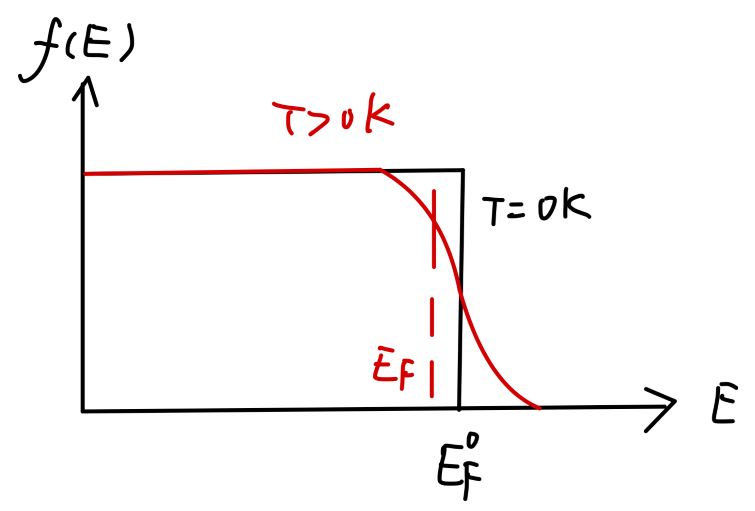
Fig：基态和激发态的分布函数

$T = 0, E_F^0 \sim 5 \mathrm{eV}$

可以定义费米温度：

$k_BT = E_F^0 \Rightarrow T_F = \frac{E_F^0}{k_B} \sim 5\times 10^4 \mathrm{K}$

室温的量级为 $T:10^2\sim 10^3 \mathrm{K}$ ，如此可以得到：

$T/T_F \sim 10^{-2}$

因此，在室温下的激发态的分布函数相比零温分布函数来说，其变化不大，且偏离仅仅限于费米能附近。

我们仍然定义 $E = E_F$ 的等能面为费米面。

分布函数为：

$f(E) = \frac{1}{1 + e^{(E - E_F)/k_BT}}$

有：

$-\frac{\partial f}{\partial E} = \frac{1}{k_BT} \frac{1}{(e^{(E-E_F)/k_BT} + 1)(e^{-(E-E_F)/k_BT} + 1)}$

考虑在远离费米面处有 $|E-E_F| \gg k_BT$

分布函数可以近似为：

$f(E) = \frac{1}{e^{(E-E_F)/k_BT}-1} \approx \left\{ \begin{aligned} & 1 & E-E_F \ll -k_BT\\ & \frac{1}{2} & E= E_F\\ & 0 & E-E_F \gg k_BT\\ \end{aligned} \right.$

并且有：

$-\frac{\partial f}{\partial E} \approx \delta(E-E_F)$

现在我们考虑费米能随温度的变化。先做一个定性的说明：对于三维系统来说，态密度在能量高处更大，在有限温度下，有更多粒子占据高能量，若费米能不变，使用该分布函数计算得到粒子数必然时增加的，由此可以得到三位体系的费米能必定随着温度升高而下降。

下面我们来定量计算费米能随温度的变化。
由：

$N = \int_{0}^{\infty}f(E)N(E)dE$

引入：

$\begin{aligned} &Q(E) = \int_{0}^{E} N(E)dE\\ &Q'(E) = N(E)\\ \end{aligned}$

得到：

$\begin{aligned} N =& \int_{0}^{\infty} f(E)Q'(E)dE\\ =& f(E)Q(E)|_{0}^{\infty} + \int_{0}^{\infty} Q(E) (-\frac{\partial f}{\partial E}) dE\\ =& \int_{0}^{\infty} Q(E) (-\frac{\partial f}{\partial E}) dE\\ =& Q(E_F) \int_{-\infty}^{\infty} (-\frac{\partial f}{\partial E})dE + Q'(E_F) \int_{-\infty}^{\infty} (E-E_F)(-\frac{\partial f}{\partial E}) dE\\ &+ \frac{1}{2}Q''(E_F) \int_{-\infty}^{\infty} (E-E_F)^2 (-\frac{\partial f}{\partial E})dE + \cdots \end{aligned}$

得到：

$N = Q(E_F) + \frac{1}{2}Q''(E_F) \int_{-\infty}^{\infty} (E-E_F)^2(-\frac{\partial f}{\partial E}) dE + \cdots$

令 $\xi = \frac{E-E_F}{k_BT}$ ，那么可以从上式得到：

$\begin{aligned} \int_{-\infty}^{\infty} (E-E_F)^2 (-\frac{\partial f}{\partial E})dE &= (k_BT)^2 \int_{-\infty}^{\infty} \frac{\xi^2d\xi}{(e^{\xi}+1)(e^{-\xi}+1)}\\ &= \frac{\pi^2}{3}(k_BT)^2\\ \end{aligned}$

得到下式，并将结果展开在 $E_F^0$ 附近展开：

$\begin{aligned} N &= Q(E_F) + \frac{\pi^2}{6} Q''(E_F)(k_B T)^2\\ &= Q(E_F^0) + Q'(E_F^0)(E_F-E_F^0) + \frac{\pi^2}{6} Q''(E_F^0)(k_B T)^2\\ &= N + Q'(E_F^0)(E_F-E_F^0) + \frac{\pi^2}{6} Q''(E_F^0)(k_B T)^2\\ \end{aligned}\tag{10}$

如此有

$E_F = E_F^0 - \frac{\pi^2}{6}\frac{Q''(E_F^0)}{Q'(E_F^0)}(k_BT)^2 \tag{11}$

在三维情况下， $N \propto E^{1/2}$ ，可以得到：

$E_F = E_F^0\{1 - \frac{\pi^2}{12}(\frac{k_BT}{E_F^0})^2\} \tag{12}$

电子热容量

激发态电子系统的总能量

$\begin{aligned} U &= \int_{0}^{\infty} Ef(E) N(E)dE\\ \end{aligned}$

引入： $R(E) = \int_{0}^{E}EN(E)dE$ 。

类比 $(10)$ 式，内能可以在费米能附近展开为：

$\begin{aligned} U(E) &= R(E_F^0) + (E_F - E_F^0)R'(E_F^0) + \frac{\pi^2}{6}R''(E_F^0)(k_BT)^2 \end{aligned}$

其中：

$\begin{aligned} &R(E_F^0) = U_0\\ & E_F - E_F^0 = - \frac{\pi^2}{12E_F}(k_BT)^2\\ & R'(E_F^0) = E_F^0 N(E_F^0)\\ & R''(E_F^0) = N(E_F^0) + E_F^0N'(E_F^0)\\ \end{aligned}$

最终得到：

$U = U_0 + \frac{\pi^2}{6} N(E_F^0)(k_BT)^2 \tag{13}$

其中第二项就是电子气的激发能，在温度 $T$ ，只有费米面附近 $k_BT$ 的电子被热激发。进一步的，得到自由电子气的比热容为：

$\begin{aligned} C_V &= (\frac{\partial U}{\partial T})|_V \\ &= \frac{\pi^2}{3} N(E_F^0)k_BT \cdot k_B\\ &= N\frac{\pi^2}{2} (\frac{k_BT}{E_F^0}) k_B\\ & = \frac{\pi^2}{2}N k_B (\frac{k_BT}{E_F^0})\\ & = \frac{\pi^2}{2}N k_B (\frac{T}{T_F^0})\\ \end{aligned}\tag{14}$