固体物理笔记（五）：晶格动力学基础

在零温时，晶体位于基态，所有原子都位于平衡位置。实际上，在任何有限温度下（或受到某种弱外场的激发），晶体中的原子都在平衡位置附近作微振动，也就是晶体位于激发态。基态和激发态的性质决定了晶体的宏观物性。从晶体中原子的振动出发去讨论晶体的宏观物性，常称为 晶格动力学 $^{[1]}$ 。

简正模与格波

简正模

设晶体中有 $N$ 个原子。那么总共有 $3N$ 个自由度，可以取 $3N$ 个位移分量 $\mu_i$ 来表示原子相对于平衡位置的偏移。引入约化坐标 $q_i = \sqrt{m_i}\mu_i$ ， $m_i$ 为第 $i$ 个原子的质量。体系的哈密顿量可以表示为：

$\begin{aligned} H &= T + V\\ &= \frac{1}{2}\sum_{i} \dot{q}_i^2 + \sum_i (\frac{\partial V}{\partial q_i})|_0 q_i + \frac{1}{2}\sum_{ij} (\frac{\partial^2 V}{\partial q_i\partial q_j})|_0q_iq_j + \cdots\\ & \approx \frac{1}{2}\sum_i \dot{q}_i^2 + \frac{1}{2}\sum_{ij}\lambda_{ij} q_iq_j \end{aligned} \tag{1}$

考虑到原子位置的偏移应当为一个小量，因此忽略了二阶以上的高阶项。最终得到了一个二次型的哈密顿量。

写做矩阵形式：

$H = \frac{1}{2}\dot{\bm{q}}^T\dot{\bm{q}} + \frac{1}{2}\bm{q}^T\bm{\lambda}\bm{q} \tag{2}$

由理论力学我们知道存在一个正交变换 $\bm{A}$ ，将坐标 $\bm{q}$ 变为简正坐标 $\bm{Q}$ ：

$\bm{q} = \bm{A}\bm{Q} \tag{3}$

对应的哈密顿量是可分的：

$\begin{aligned} H &= \frac{1}{2}\dot{\bm{q}}^T\dot{\bm{q}} + \frac{1}{2}\bm{q}^T\bm{\lambda}\bm{q}\\ &= \frac{1}{2}\dot{\bm{q}}^T\dot{\bm{q}} + \frac{1}{2}\bm{q}^T\bm{\lambda}\bm{q}\\ &= \frac{1}{2}\dot{\bm{Q}}^T\dot{\bm{Q}} + \frac{1}{2}\bm{Q}^T\bm{\omega}^2\bm{Q}\\ &=\frac{1}{2}\sum_{j}(\dot{Q}_j^2+\omega_j^2Q_j^2)\\ &=\frac{1}{2}\sum_{j}(P_j^2+\omega_j^2Q_j^2)=\sum_{j}H_j\\ \end{aligned} \tag{4}$

对应的运动方程为：

$\ddot{Q}_j + \omega_j^2 Q_j = 0\quad i =1,2,\cdots,3N\tag{5}$

得到的解：

$Q_j = Ae^{-i\omega_j t}$

所有的简正模构成一个正交完备基。晶格的任一振动可以表示为它们的线性组合。采用一次量子化方法过渡到量子理论：

一次量子化方法：即用物理量用算子代替（以下为坐标表象）：

$\begin{aligned} & Q_j \rightarrow \hat{Q}_j = Q_j\\ & P_j \rightarrow \hat{P}_j = \frac{\hbar}{i}\frac{\partial}{\partial Q_j}\\ \end{aligned}$

$\sum \frac{1}{2}(-\hbar^2\frac{\partial^2}{\partial Q_j^2} + \omega_j^2Q_j^2) \psi(Q_1,Q_2,\cdots,Q_{3N}) =E\psi(Q_1,Q_2,\cdots,Q_{3N})\tag{7}$

哈密顿变量可分意味着可以薛定谔方程可以进行分离变量 $\psi(Q_1,Q_2,\cdots,Q_{3N}) = \prod_{j=1}^{3N}\varphi(Q_j)$ ：

$\frac{1}{2}(-\hbar^2\frac{\partial^2}{\partial Q_j^2} + \omega_j^2Q_j^2)\varphi(Q_j) = E_j\varphi(Q_j)\tag{6}$

对应的本征能量与本征波函数为：

$\left\{ \begin{aligned} & \varepsilon_j = (n_j + \frac{1}{2})\hbar\omega_j\\ & \varphi_{n_j}(Q_j) = \sqrt{\frac{\omega_j}{\hbar}}\exp(-\frac{\xi^2}{2})H_{n_j}(\xi) \end{aligned}\tag{7} \right.$

其中 $\xi = \sqrt{\frac{\omega_j}{\hbar}}Q_j$ ， $H_n$ 表示厄米多项式。

格波

简正坐标 $Q_j$ 描述的振动为：系统中每个原子均以相同的频率 $\omega_j$ 振动，其对时间的依赖关系为 $\exp(-\omega_j t)$ ，因为它是系统的本征振动，所以其幅度应当不依赖时间。一般地，频率为 $\omega_j$ 的简正模可写为：

$e^{-i\omega_j t}f(\bm{r})$

现在考虑简单晶格。由于晶格的平移对称性，每个格点处的振幅应当是相等的，不同格点处的振动至多相差一个相位。

考虑相邻原子间振动的相位差

$\begin{aligned} & f(\bm{a}_1) = e^{iq_1a_1} f(0)\\ & f(\bm{a}_2) = e^{iq_2a_2} f(0)\\ & f(\bm{a}_3) = e^{iq_3a_3} f(0)\\ \end{aligned}$

引入的物理量 $\bm{q}=(q_1,q_2,q_3)$ 称为波矢。

一般地，任意格点 $\bm{R}_l$ 上原子的振幅为：

$\begin{aligned} f(\bm{R}_l) &= e^{i(l_1q_1a_1+l_2q_2a_2+l_3q_3a_3)}f(0)\\ &=e^{i\bm{q}\cdot\bm{R}_l} f(0)\\ \end{aligned}$

由此可以得到晶体中原子振动的解：

$A_{j\sigma}e^{i(\bm{q}\cdot\bm{R}_l-\omega(\bm{q})t)}\tag{8}$

$A_{j\sigma}$ 是特定振动模式，偏振方向对应的振动幅度。
由于晶格的不连续性，波的振幅只在只在格点上定义，称为格波。一个 $N$ 原子的晶体，总共存在 $3N$ 个自由度，存在 $3N$ 个独立的谐振子，等价于 $3N$ 个独立的格波（ $\omega_j,\bm{q}$ ）。

晶格振动

一维单原子链振动

考虑将两个原子之间的相互作用势作如下形式的展开：

$V(a+\delta) = V(a) + \frac{1}{2}\beta \delta^2 + O(\delta^3)+\cdots$

近似：忽略非简谐项、忽略次近邻原子的作用。

$M\ddot{u}_n = -\beta(u_n-u_{n-1})-\beta(u_n-u_{n+1}) =\beta(u_{n+1}+u_{n-1}-2u_n)$

带入如下试探解：

$u_n = Ae^{i(qna-\omega t)}$

得到 色散关系：

$\omega = 2\sqrt{\frac{\beta}{M}}|\sin(\frac{1}{2}qa)|\tag{9}$

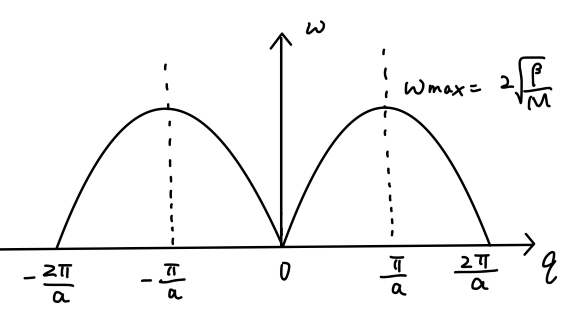
Fig：维单原子链振动的色散关系

对于 $q\rightarrow 0$ （长波极限或连续介质极限），色散关系退化为：

$\omega(q) =\sqrt{\frac{\beta}{M}}aq= cq \tag{10}$

此时，声速 $c$ 不依赖于频率，这与弹性波再连续介质中传播的情形一样。一个确定的 $q$ 与 $\omega(q)$ 就确定一个简正模。根据色散关系 $(9)$ ， $\omega(q)$ 是一个倒空间中的周期函数：

$\omega(q) = \omega(q+\frac{2\pi}{a})$

更一般的，有：

$\omega(q) = \omega(q+K_h) \tag{11}$

这表明 $q,q+K_h$ 表示同一个振动模式。换句话说，独立的波矢在一个倒格子元胞里。我们常常把波矢取在第一布里渊区内。

从一维单原子链的例子中，我们已经可以看到：在周期性结构中传播的波，频谱成带结构。对于单原子链，频率大于 $\omega_{max}$ 的波无法在系统中传播。

Born-Karman 条件

以上讨论的是无穷大的晶体（或无穷长的原子链）。对于有限大晶体，以上讨论不适用，因为对于边界粒子，其运动方程的形式会发生变化。现在我们考虑引入一个边界条件，使得无穷大情况下的方程能够应用于有限大情形。我们引入 Born-Karman 条件，对于一个 $N$ 原子的链，有：

$u_n = u_{n+N} \tag{12}$

通过引入一个周期性边界条件，简化了有限晶体的计算。当然这种方式反映不了晶体表面的特征，但是对于一个晶体来说，往往内部的原子比表面原子多的多，这种简化是适用。形象的来说，对于原子链，Born-Karman 条件将其转化为了一个环。以下我们简称 Born-Karman 条件为 BK 条件。

周期性条件意味着：

$e^{i(qna-\omega t)}=e^{i(q(n+N)a-\omega t)} \Rightarrow e^{iqNa} = 1 \tag{13}$

得到：

$q = \frac{2\pi h}{Na},q\in 1\mathrm{BZ} \tag{14}$

这意味着 $q$ 在 $1\mathrm{BZ}$ 内均匀分布，且只能取 $N$ 个值。

在 BK 条件下，所有的独立振动模式构成正交、完备集：

$\left\{\begin{aligned} &\frac{1}{N} \sum_{q}e^{i(n-n')aq} = \delta_{nn'}\\ &\frac{1}{N} \sum_{n}e^{i(q-q')an} = \delta_{qq'}\\ \end{aligned} \right.\tag{15}$

$U_{nq} = A_q e^{i(qna-\omega t)}$

原子的一般运动为所有格波的叠加：

$U_n = \sum_{l}u_{nq} =\sum_{l}A_q e^{i(naq-\omega_qt)}\tag{16}$

晶格的一般振动是所有独立模式 $\frac{1}{\sqrt{N}}e^{inaq}$ 的线性组合。

一维双原子链振动

考虑如下一维双原子链，总共有 $N$ 个元胞，每个元胞中有两个原子，总共有 $2N$ 个自由度。

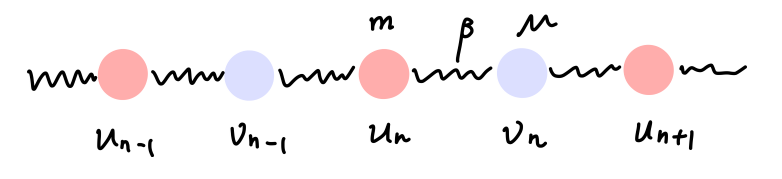
Fig：一维双原子链

运动方程为：

$\left\{ \begin{aligned} &M\frac{d^2v_n}{dt^2} = \beta(u_{n}+u_{n+1}-2v_{n})\\ &m\frac{d^2u_n}{dt^2} = \beta(v_{n-1}+v_{n}-2u_{n})\\ \end{aligned} \right.\tag{17}$

采取试探解为：

$\left\{ \begin{aligned} u_n &= Ae^{i(q\pi a-\omega t)}\\ v_n &= Be^{i(q\pi a-\omega t)}\\ \end{aligned} \right.$

得到色散关系：

$\omega^2 = \beta \frac{m+M}{mM}\{1\pm\sqrt{1-\frac{4mM}{(m+M)^2}\sin^2\frac{1}{2}qa}\}\tag{18}$

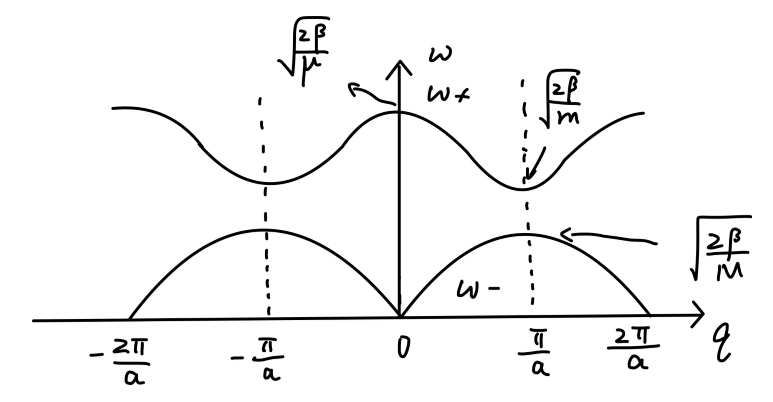
Fig：一维双原子链振动的色散关系

得到的两支色散关系分别为 声频支 与 光频支。

$\omega_{-}$ ：声频支：

$\left\{ \begin{aligned} &q=0,\quad \omega_{min}=0\\ &q=\pm\frac{\pi}{a},\quad \omega_{max}=\sqrt{\frac{2\beta}{M}}\\ \end{aligned} \right.$

$\omega_{+}$ ：光频支：

$\left\{ \begin{aligned} &q=0,\quad \omega_{max}=\sqrt{\frac{2\beta}{\mu}},\mu = \frac{mM}{m+M}\\ &q=\pm\frac{\pi}{a},\quad \omega_{min}=\sqrt{\frac{2\beta}{m}}\\ \end{aligned} \right.$

对于一般晶体，估算 $\omega^{+}(0)\approx 10^{12}\sim 10^{14}\mathrm{Hz}$ 。

现在讨论声学波与光学波的运动特征。可以从 $(17)$ 得到振动的复相位：

$a_{\pm} = (\frac{B}{A})_{\pm} = -\frac{M\omega_{\pm}^2-2\beta}{\beta(1+e^{-iqa})}$

考虑长波近似 $q\rightarrow 0$ ，得到：

长声学波

$\omega_{-}(q\rightarrow 0) = \sqrt{\frac{\beta}{2(M+m)}}aq,\quad \lim_{q\rightarrow 0}a_{-} = 1$

可得长声学波表示元胞中原子的同向运动。

长光学波

$\lim_{q\rightarrow 0}\omega_{+} = \sqrt{\frac{2\beta}{\mu}},\quad \lim_{q\rightarrow 0}a_{+} = -\frac{M}{m}$

我们发现在长光学波中，元胞的质心不动，由此长光学波表示元胞中原子的相对运动。

总结如下：

色散曲线分为两支（每个元胞里由两个自由度）：质心自由度 $(\omega_{-})$ 与相对自由度 $(\omega_{+})$ 。其间存在频率的禁带，不存在处于该区域内的本征振动。
由于晶格的不连续性， $\omega_{\pm}(q)=\omega_{\pm}(q+K_h)$
由 BK 条件， $q$ 在 $1\mathrm{BZ}$ 内取 $N$ 个值。
独立模式数等于系统自由度数。

三维晶格振动

现在将晶格振动推广到三维晶格振动的情形。考虑晶体共有 $N$ 个元胞，每个元胞中 $n$ 个原子，总自由度 $3nN$ 个，每个元胞的自由度为 $3n$ ，其中质心坐标自由度为 $3$ ，元胞内相对运动坐标 $3n-3$ 。

对于 $n$ 个不同的原子，我们列出 $3n$ 个运动方程，得到 $3n-3$ 个光频支（ $2(n-1)$ 支横波， $n-1$ 支纵波）与 $3$ 个声频支（ $2$ 支横波， $1$ 支纵波）。考虑 BK 条件，每一支可以取 $N$ 个 $\bm{q}$ 值（独立的波矢）。由此，总共存在 $3nN$ 个独立的振动模式，这就等于系统的自由度数目。

声子

在三维晶格振动中有如下对应关系：

一个 $\omega_s(\bm{q})$ , $\bm{q}$ 的格波 $\Longleftrightarrow$ 简正坐标 $Q(\bm{q},s)$ 描述的谐振子 $(3nN)$

每个谐振子的能量为：

$\varepsilon_{q,s} = (n_{q,s}+\frac{1}{2})\hbar\omega_s,\quad n=0,1,2,\cdots\tag{19}$

$\omega_s$ 确定的振动模处于 $(n_{qs}+\frac{1}{2})\hbar\omega_s$ 的本征态，称为有 $n_{q,s}$ 个声子， $n_{qs}$ 为声子数。声子是格波的量子。声子是一种准粒子。

现在讨论声子的一些性质：

声子是玻色子

考虑温度为 $T$ 时声子的正则配分函数：

$\beta = (k_BT)^{-1}$

$\begin{aligned} Z &= \sum_{n=0}^{\infty} e^{-\beta n_{q,s}\hbar\omega_{q,s}}\\ &= \frac{1}{1 - e^{-\beta\hbar\omega_{q,s}}}\\ \end{aligned}\tag{20}$

对应一个简正模的平均声子数为：

$\begin{aligned} \langle n \rangle &= -\frac{1}{\hbar\omega_{q,s}}\frac{\partial \mathrm{ln}Z}{\partial \beta}\\ &=\frac{1}{e^{\beta\hbar\omega_{q,s}}-1} \end{aligned}\tag{21}$