固体物理笔记（六）：离子晶体中的长光学波、晶体的热学性质

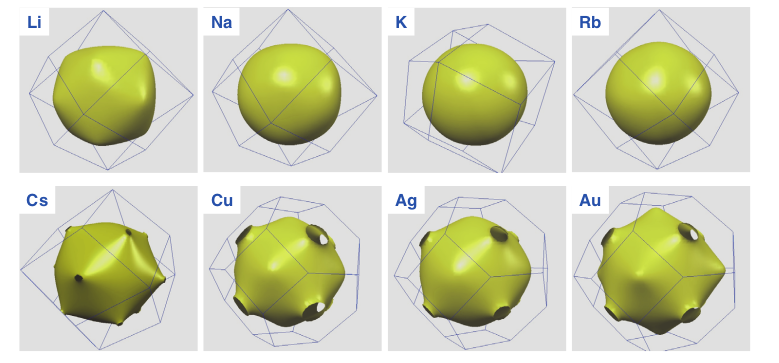
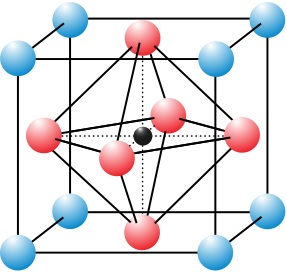
离子晶体中的长光学波

在离子晶体中，长光学波代表元胞内正、负离子的反向运动，这将伴随着 晶体极化，并产生内场。这对离子晶体的电学、光学性质有重要影响。

在离子晶体长光学晶格振动，设正、负离子相对位移为 $\bm{u}_{+},\bm{u}_{-}$ ，这导致的极化强度矢量为：

$\bm{P} = \frac{1}{\Omega} q^* (\bm{u}_{+} - \bm{u}_{-})\tag{1}$

其中 $q^*$ 为离子携带的有效电荷。其大小正比于正负离子相对位移，考虑到正负离子运动的格波解，极化强度也应当随着位置、时间周期性变化，有：

$\bm{P} = \bm{P}_0 e^{i(\bm{q}\cdot\bm{r}-\omega t)}\tag{2}$

由电动力学，可以得到极化产生的宏观内场：

$\bm{E} = \frac{\omega^2/c^2 \bm{P}-\bm{q}(\bm{q}\cdot\bm{P})}{\varepsilon_0(q^2-\omega^2/c^2)} \tag{3}$

以下分纵波与横波具体讨论：

对于纵波来说： $\bm{P} \parallel \bm{q}$
可得

$\bm{E}_L = -\frac{\bm{P}}{\varepsilon_o} \tag{4}$

此时的电场平行于波矢，旋度为零，无伴生磁场。此时宏观电场的作用力使得总的恢复力变大，对应的纵模振动频率 $\omega_{LO}$ 应当变高。

对于横波来说： $\bm{P}\perp \bm{q}$
可得

$\bm{E} = \frac{\omega^2}{\varepsilon_0(q^2c^2-\omega^2)}\bm{P}\tag{5}$

此时电场垂直于波矢，横模伴随的内场是一种由磁场相伴的有旋场。在 $\omega = qc$ 时发生共振。

长光学波的宏观运动方程

定义如下向量来描述正负离子间的相对位移

$\bm{W} = (\bm{u}_{+}-\bm{u}_{-}) (\frac{\mu}{\Omega})^{1/2}\tag{6}$

其中 $\mu$ 为正负离子的折合质量， $\omega$ 为原胞体积。

考虑拉格朗日密度。其中动能密度为：

$T = \frac{1}{2}\dot{\bm{W}}^2 \tag{7}$

势能密度可以写为两部分：

$V = -\int \bm{F}\cdot d\bm{W}-\int \bm{P}\cdot d\bm{E}\tag{8}$

其中 $\bm{F}$ 为弹性恢复力， $(8)$ 式中两项分别表示弹性势能与极化能。在近似下有：

$\bm{F} = b_{11}\bm{W},\bm{P}=b_{12}\bm{W} + b_{22}\bm{E}\tag{9}$

势能可由此算出，结合 $(8),(9)$ ，有：

$V = -\frac{1}{2}b_{11}\bm{W}^2 - b_{12}\bm{W}\cdot\bm{E}-\frac{1}{2}b_{22}\bm{E}^2\tag{10}$

于是得到拉格朗日密度为：

$L = \frac{1}{2}\dot{\bm{W}}^2+\frac{1}{2}b_{11}\bm{W}^2 + b_{12}\bm{W}\cdot\bm{E}+\frac{1}{2}b_{22}\bm{E}^2\tag{11}$

写出对应的运动方程：

$\ddot{\bm{W}}= b_{11}\bm{W} + b_{12} \bm{E}$

该式与 $(9)$ 式可以合写为：

以下有 $b_{21} = b_{12}$

$\left\{ \begin{aligned} \ddot{\bm{W}}&= b_{11}\bm{W} + b_{12} \bm{E}\\ \bm{P}&= b_{21}\bm{W} + b_{22} \bm{E}\\ \end{aligned} \right.\tag{12}$

这称为 黄昆方程，它是描述离子晶体中长光学波的基本方程。其中系数 $b_{11},b_{12},b_{22}$ 被称为 动力学系数。

通过实验测量，可以确定动力学系数。考虑一些极端情况：

$\bm{E}$ 为恒定静电场，对应正负粒子产生恒定位移，并不振动 $(\omega = 0)$ 。此时有：

$\bm{P} = (b_{22}-\frac{b_{12}^2}{b_{11}})\bm{E} \tag{13}$

对应有：

$(\varepsilon(0)-1)\varepsilon_0 = b_{22}-\frac{b_{12}^2}{b_{11}}\tag{14}$

$\varepsilon(\omega)$ 为介电函数，描述离子晶体的介电常量随频率的变化。

$\bm{E}$ 为高频电场， $\omega\gg \omega_{TO},\omega_{LO}$ 。此时离子运动频率远远小于电场频率，可得 $\bm{W}\approx 0$ ，在此近似下有：

$\bm{P} = b_{22}\bm{E} \tag{15}$

对应的：

$(\varepsilon(\infty)-1)\varepsilon_0=b_{22} \tag{16}$

考虑横模的本征振动，其本征频率与电场无关。令 $\bm{E} = 0$ ，得到：

$\ddot{\bm{W}} = b_{11}\bm{W}$

对应有：

$\omega_{TO}^2 = -b_{11} \tag{17}$

综上，通过测量介电常量 $\varepsilon(0)$ 与 $\varepsilon(\infty)$ ，晶格的横模频率 $\omega_{TO}$ ，根据 $(14),(16),(17)$ 就可以计算相应的动力学系数：

$\left\{ \begin{aligned} & b_{11} = -\omega_0^2\\ & b_{12} = b_{21} = [\varepsilon(0)-\varepsilon(\infty)]^{1/2} \varepsilon_0^{1/2} \omega_0\\ & b_{22} = [\varepsilon(\infty)-1]\varepsilon_0\\ \end{aligned} \right.\tag{18}$

离子晶体长光学波的本征频率

现在讨论无横场耦合时系统的本征振动。

不存在外磁场，同时忽略横向极化伴随的有旋场。

将黄昆方程与麦克斯韦方程组联立：

$\left\{ \begin{aligned} &\ddot{\bm{W}} = b_{11}\bm{W} + b_{12}\bm{E}\\ &\bm{P} = b_{21}\bm{W} + b_{22}\bm{E}\\ &\nabla\times\bm{E} = -\mu_0 \frac{\partial}{\partial t} \bm{H},\mu_r =1 \\ & \nabla\times \bm{H} = \frac{\partial}{\partial t}\bm{D}\\ & \nabla\cdot\bm{D}=0\\ & \nabla\cdot\bm{H}=0\\ \end{aligned} \right.\tag{19}$

代入试探解：

$\left\{ \begin{aligned} &\bm{W} = \bm{W}_0 e^{i(\bm{q}\cdot\bm{r}-\omega t)}\\ &\bm{P} = \bm{P}_0 e^{i(\bm{q}\cdot\bm{r}-\omega t)}\\ &\bm{E} = \bm{E}_0 e^{i(\bm{q}\cdot\bm{r}-\omega t)}\\ &\bm{H} = \bm{H}_0 e^{i(\bm{q}\cdot\bm{r}-\omega t)}\\ \end{aligned} \right.\tag{20}$

得到：

$\left\{ \begin{aligned} & -\omega^2 \bm{W}_0 = b_{11}\bm{W}_0 + b_{12}\bm{E}_0\\ &\bm{P}_0 = b_{21}\bm{W}_0 + b_{22}\bm{E}_0\\ & \bm{q}\times \bm{E}_0 = \mu_0\omega\bm{H}_0\\ & \bm{q}\times \bm{H}_0 = -\omega(\varepsilon_0\bm{E}_0+\bm{P})\\ & \bm{q}\cdot(\varepsilon_0\bm{E}_0+\bm{P}) = 0\\ & \bm{q}\cdot\bm{H}_0 = 0\\ \end{aligned} \right.\tag{21}$

由上方程组 $1,2$ 式得到：

$\bm{P}_0 = [-\frac{b_{12}^2}{b_{11}+\omega^2}+b_{22}]\bm{E}_0 \tag{22}$

代入 $(21.5)$ 得到：

$(\bm{q}\cdot\bm{E}_0)(\varepsilon_0 -\frac{b_{12}^2}{b_{11}+\omega^2}+b_{22}) = 0 \tag{23}$

对于纵波（ $\bm{q}\cdot\bm{E}_0\neq 0$ ），有：

$\varepsilon_0 -\frac{b_{12}^2}{b_{11}+\omega^2}+b_{22} = 0 \tag{24}$

对应有：

$\omega^2_{LO} = -(b_{11}-\frac{b_{12}^2}{\varepsilon_0+b_{22}}) = [\frac{\varepsilon(0)}{\varepsilon(\infty)}] \omega_{TO}^2 \tag{25}$

这称为 LST 关系（Lyddane-Sachs-Teller）。静电介电常数 $\varepsilon(0)$ 表示晶体中所有带电粒子的效应，而高频介电常量 $\varepsilon(\infty)$ 表示电子的效应。一般来说， $\varepsilon(0)>\varepsilon(\infty)$ ，因此离子晶体中的长光学纵波频率 $\omega_{LO}$ 总是大于五耦合长光学波横波的频率 $\omega_{TO}$ 。对于非离子晶体，晶格振动不产生位移极化，由此 $b_{12}=0$ ，对应有 $\omega_{TO} = \omega_{LO}$

极化激元

现在讨论光学模声子与电磁波的相互作用，在共振条件下，声子-光子耦合将导致全新的色散关系。耦合声子-光子场的量子称为 极化激元。

我们继续上一节对联立的黄昆方程，麦克斯韦方程 $(21)$ 的求解。继续考虑横波解。此时由 $(21.3-4)$ 得到：

$\left\{ \begin{aligned} & qE_0 -\mu_0\omega H_0 = 0\\ & \omega(\varepsilon_0 -\frac{b_{12}^2}{b_{11}+\omega^2}+b_{22})E_0 - qH_0 = 0\\ \end{aligned}\tag{26} \right.$

利用该方程组有解的条件，得到：

$\frac{q^2}{\mu_0\omega^2} = \varepsilon_0 -\frac{b_{12}^2}{b_{11}+\omega^2}+b_{22} \tag{27}$

利用 LST 关系 $(25)$ 以及动力学系数的表达式 $(18)$ ，可以将上述式子重新写为：

$\frac{c^2q^2}{\omega^2} = \varepsilon(\infty)\frac{\omega_{LO}^2-\omega^2}{\omega_{TO}^2-\omega^2}\tag{28}$

解得：

$\omega_{\pm} = \frac{1}{2}\{\frac{c^2q^2}{\varepsilon(\infty)}+\omega_{LO}^2 \pm [\omega^4_{LO} + \frac{2c^2q^2}{\varepsilon(\infty)}(\omega_{LO}^2-2\omega_{TO}^2)+\frac{c^4q^4}{\varepsilon^2(\infty)}]^{1/2}\} \tag{29}$

极化激元得色散关系分为 $\omega_{\pm}(q)$ 两支。

当 $q\rightarrow 0$

$\begin{aligned} &\omega_{+} \approx \omega_{LO} \\ &\omega_{-} \approx \frac{qc}{\sqrt{\varepsilon(0)}} \\ \end{aligned}\tag{30}$

我们发现在长波段： $\omega_{+}$ 的色散关系类似于声子，称为 类声子； $\omega_{-}$ 的色散关系类似于低频光子，称为 类光子。

当 $q\gg \omega_{LO}\sqrt{\varepsilon_{\infty}}/c$ 时：

$\begin{aligned} &\omega_{+} \approx \omega_{TO} \\ &\omega_{-} \approx \frac{qc}{\sqrt{\varepsilon(\infty)}} \\ \end{aligned}\tag{31}$

我们发现在短波段： $\omega_{-}$ 的色散关系类似于声子，称为 类声子； $\omega_{+}$ 的色散关系类似于高频光子，称为 类光子。

在共振区，出现了光子与声子的混合模式。出现了一个频率传播的禁带，对应频率的电磁波无法在晶体中传播，相应的反射率达到最大。

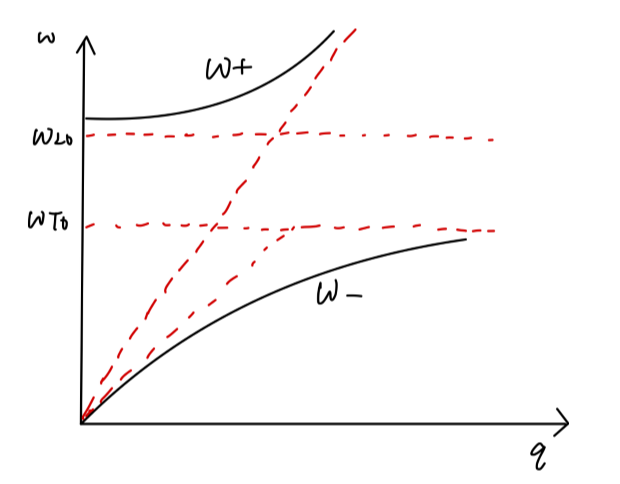
Fig：声光耦合的色散关系

晶体的热学性质

晶格比热容

按照经典统计力学的结论，能量按照自由度均分，对固体来说，每个原子都有三个自由度，且每个自由度的动能与势能相等均为 $\frac{1}{2}k_BT$ ，此时：

$U = 3Nk_BT$

于是固体的比热容为：

$C_V = (\frac{\partial U}{\partial T})_V = 3Nk_B = 3nR$

按照经典理论，比热容应当为一个常数。然而实验发现，在高温时，比热容确实接近一个常数，但当温度趋近于绝对零度时，比热容也趋近于零，且有：

$C_V \propto T^3$

这点是经典物理所不能解释的。接下来，我们对这个问题进行考虑。

声子谱密度

在温度为 $T$ 时，晶格的平均能量为：

$E(T) = \sum_{q,s}(n_{q,s}(T) + \frac{1}{2})\hbar\omega_{s}(\bm{q})\tag{32}$

其中 $n_{q,s} = [e^{\hbar\omega/k_BT}-1]^{-1}$ 表示温度为 $T$ 时，波矢为 $\bm{q}$ 、频率为 $\omega_{s}$ 的平均声子数，对总共 $3nN$ 个模式进行求和。晶格的定容比热容为：

$\begin{aligned} C_V(T) & = \frac{\partial E(T)}{\partial T}|_V \\ & = \sum_{q,s}k_B \frac{[\frac{\hbar\omega_s(\bm{q})}{k_BT}]^2e^{\hbar\omega_s(\bm{q})/k_BT}}{(e^{\hbar\omega_s(\bm{q})/k_BT}-1)^2}\\ & = \sum_{q,s} C(\omega_s(\bm{q})) \end{aligned}\tag{33}$

其中 $C(\omega_s(\bm{q}))$ 表示模式为 $\bm{q},s$ 的声子对晶格比热容的贡献。考虑 $\bm{q}$ 在 $q$ 空间中准连续分布，因此可以将求和改为在 $1BZ$ 内的积分：

$C_V(T) =\frac{V}{(2\pi)^3} \sum_s \int_{\Omega^*} C(\omega_s(\bm{q}))d\bm{q}\tag{34}$

考虑到波矢 $\bm{q}$ 与 $\omega$ 是存在关系的（色散关系），我们考虑将 $(34)$ 式改写为：

$C_V(T) =\sum_s \int_{0}^{\infty}\rho(\omega)C(\omega)d\omega\tag{35}$

其中 $\rho(\omega)$ 为 声子谱密度，这由色散关系决定。通过 $(35)$ 式，我们把在倒格子上的三重积分变为了在频域上的一重积分。我们现在考虑声子谱密度，其定义如下：

$\begin{aligned} \rho(\omega) &= \frac{V}{(2\pi)^3}\sum_s\int_{\Omega^*}d\bm{q}\delta(\omega-\omega_s(q))\\ &= \frac{V}{(2\pi)^3}\sum_s\int_{\Omega^*}dqdS_{\omega}\delta(\omega-\omega_s(q))\\ & = \frac{V}{(2\pi)^3}\sum_s\int \frac{dS_{\omega}}{|\nabla\omega_s(\bm{q})|} \end{aligned}\tag{36}$

容易得到，将 $(36)$ 式代入 $(35)$ 式将得到 $(34)$ 式。且如此选取的声子谱密度具有如下性质：

$\begin{aligned} \int_{0}^{\infty} \rho(\omega)d\omega &= \frac{V}{(2\pi)^3}\sum_s\int_{0}^{\infty}\int_{\Omega^*}\delta(\omega-\omega_s(q)) d\bm{q}d\omega\\ &= \frac{V}{(2\pi)^3}\sum_s\int_{\Omega^*}d\bm{q}\\ & = \frac{V}{(2\pi)^3} \sum_s \Omega^*\\ & = 3nN\\ \end{aligned}\tag{37}$

即所有频率的声子谱密度加起来正好等于系统的自由度数目，这点是很好的。

接下来，我们将考虑具体的色散关系，求出声子谱密度和对应的晶格比热容。我们具体考虑两种模型：

Einstein 模型

晶体中所有原子都以同一频率振动
Debye 模型

连续介质近似

其中，Einstein 模型是比较简单的，但是其能够导出 $C_V$ 随着 $T\rightarrow 0$ 而趋于零的结果。较为复杂的 Debye 模型能够导出正确的热容随温度变化规律（低温或高温时）。接下来，我们来具体说明这件事情。

Einstein 模型

现在考虑 Einstein 模型：晶体中所有原子都以 同一频率振动，相互独立。

$\omega_S(\bm{q}) = \omega_E\tag{38}$

Einstein 模型的声子谱密度为：

$\begin{aligned} \rho(\omega)&=\frac{V}{(2\pi)^3}\sum_s\int_{\Omega^*}d\bm{q}\delta(\omega-\omega_E)\\ &=\frac{V}{(2\pi)^3}\delta(\omega-\omega_E)\sum_s\int_{\Omega^*}d\bm{q}\\ &=3nN\delta(\omega-\omega_E)\\ \end{aligned}\tag{39}$

我们使用 $C^E_V(T)$ 来表示 Einstein 模型给出的比热容。

$\begin{aligned} C_V^E(T) &= \int_{0}^{\omega}\rho_E(\omega)C(\omega)d\omega \\ & = 3nNk_B\frac{(\beta\hbar\omega_E)^2e^{\beta \hbar\omega_E}}{(e^{\beta\hbar\omega_E}-1)^2} \end{aligned}\tag{40}$

定义爱因斯坦温度 $T_E = \hbar\omega_E/k_B$ 。

在高温近似下 $T \gg T_E$ ，有：

$C_V^E(T) = 3nNk_B \tag{41}$

在低温近似下 $T \ll T_E$ ，有：

$C_V^E(T) = 3nNk_B(\beta\hbar\omega_E)^2e^{-\beta\hbar\omega_E}\tag{42}$

与实验数据做对比，进行拟合可以给出 $\omega_E$ 的确定。与经典比热比较，Einstein 模型更正确。 $T\gg T_E$ 时与经典比热一致， $T\ll T_E$ 时： $T\rightarrow 0,C\rightarrow 0$ （尽管不能给出正确的趋近行为）。

显然，Einstein 模型的粗糙之处很明显：它假设所有原子都以同一频率振动，这点当然和实际不相符，实际晶格中存在各种各样的振动频率。

Debye 模型

Debye 将晶体当作连续介质处理，也就是考虑晶体中的长波声学模，此时色散关系为：

$\omega_s(q) = \left\{ \begin{aligned} &c_l q \quad LA\\ &c_t q \quad TA\\ \end{aligned}\tag{43} \right.$

其中 $c_l$ 、 $c_t$ 分别为 纵波声速 与 横波声速（一般来说， $c_l>c_t$ ）。理想的连续介质是一个拥有无穷自由度的体系，因此这样得到的比热容必定是发散的。因此我们考虑截断近似，我们假设所有可能的波矢位于一个半径为 $q_{D}$ 的德拜球内，我们使用这个德拜球去代替布里渊区，由此得到：

$\frac{4\pi}{3}q_D^3 = \Omega^* = \frac{(2\pi)^3}{\Omega} = \frac{(2\pi)^3N}{V}$

得到：

$q_D = (\frac{6\pi^2N}{V})^{1/3} \tag{44}$

Debye 截止频率为：

$\omega_D = (\frac{6\pi^2N}{V})^{1/3} \bar{c} \tag{45}$

其中 $\bar{c}$ 为平均声速：

$\frac{3}{\bar{c}^3} = \frac{1}{c^3_l} + \frac{2}{c^3_t}$

声子谱密度：

$\begin{aligned} \rho_D(\omega) &= \frac{V}{(2\pi)^3} \sum_s\int\frac{dS_\omega}{|\nabla_q\omega_s(\bm{q})|}\\ & = \frac{V}{(2\pi)^3}\sum_s \frac{4\pi q^2}{c_s}\theta(\omega_D-\omega)\\ & = \frac{V\omega^2}{2\pi^2}\theta(\omega_D-\omega)\sum_s \frac{1}{c_s^3}\\ &= \frac{V\omega^2}{2\pi^2}\frac{3}{\bar{c}^3}\theta(\omega_D-\omega)\\ & = \frac{9N\omega^2}{\omega^3_D}\theta(\omega_D-\omega)\\ & = \left\{ \begin{aligned} &\frac{9N\omega^2}{\omega^3_D}\quad & 0 \leqslant \omega \leqslant \omega_D \\ &0&\omega>\omega_D \end{aligned} \right. \end{aligned}\tag{46}$

我们使用 $C^D_V(T)$ 来表示 Debye 模型给出的比热容。

$\begin{aligned} C_V^D(T) &= \int_{0}^{\infty}\rho_D(\omega)C(\omega)d\omega \\ & = \int_{0}^{\omega_D}\frac{9N\omega^2}{\omega^3_D}k_B\frac{(\beta\hbar\omega)^2e^{\beta \hbar\omega}}{(e^{\beta\hbar\omega}-1)^2} d\omega\\ \end{aligned}\tag{47}$

使用无量纲两 $\xi = \hbar\omega/k_BT$ 作代换，并且定义德拜温度 $\theta_D = \hbar\omega/k_B$ ，因此 $(47)$ 给出：

$C_V^D = 9Nk_B (\frac{T}{\theta_D})^3 \int_{0}^{\theta_D/T} \frac{\xi^4e^{\xi}}{(e^{\xi}-1)^2} d\xi \tag{48}$

我们考虑在高温极限与低温极限下，Debye 模型给出的比热容。

高温极限 $T \gg \theta_D\Rightarrow \xi\ll 1$

$\begin{aligned} C^D_V &\approx 9Nk_B (\frac{T}{\theta_D})^3 \int_{0}^{\theta_D/T} \xi^2d\xi\\ &= 9Nk_B (\frac{T}{\theta_D})^3 \frac{1}{3}(\frac{\theta_D}{T})^3\\ & = 3Nk_B = 3nR\\ \end{aligned}\tag{49}$

低温极限 $T \ll \theta_D\Rightarrow \theta_D/T \gg 1$

$\begin{aligned} C^D_V &\approx 9Nk_B (\frac{T}{\theta_D})^3 \int_{0}^{\infty} \frac{\xi^4e^{\xi}}{(e^{\xi}-1)^2} d\xi &= 3Nk_B \frac{4\pi^4}{5}(\frac{T}{\theta_D})^3\\ & = \frac{12}{5}\pi^4 Nk_B(\frac{T}{\theta_D})^3 \\ \end{aligned}\tag{50}$

可以通过声速的测量得到 $\bar{v}$ 。德拜模型给出的结果在低温区与高温区与实验都符合的很好。但在中温区域，德拜模型与实验存在一定差距。原因为在中温区域，德拜模型所考虑的连续介质与实际的晶格的激发模式出现较大差别。我们以一维情况为例，我们比较一维连续介质和一维单原子链的色散关系与声子谱密度。

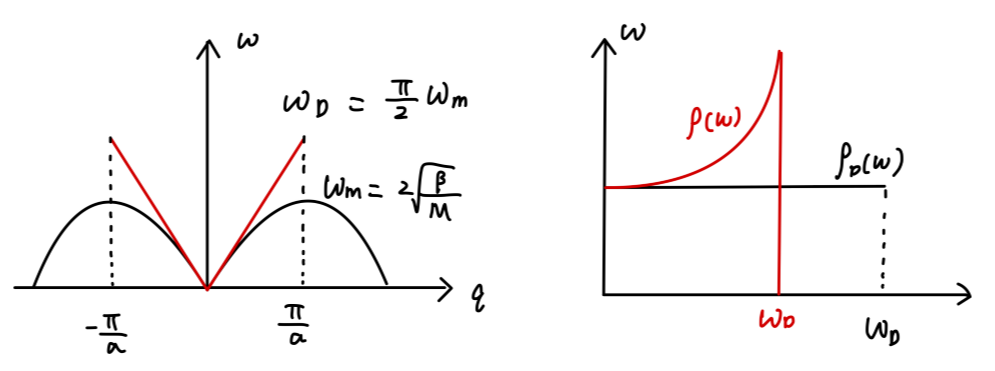
Fig：一维连续介质和一维单原子链的色散关系与声子谱密度

晶格的状态方程

晶体的内能包括基态能量 $U^0$ 和热振动能量 $U^V$ 两部分。

$U(T,V) = U^0 + U^V(T,V)\tag{51}$

$U^0$ 是基态能量，为结合能。只是体积的函数。晶体的平均热振动能量为：

$\begin{aligned} U^V(T,V) &= \sum_{j} (\bar{n}_j+\frac{1}{2})\hbar\omega_j\\ & = \int_{0}^{\infty} \rho(\omega) [\frac{1}{e^{\hbar\omega/k_BT}-1}+\frac{1}{2}]\hbar\omega d\omega\\ \end{aligned}\tag{52}$

系统的自由能为：

$\begin{aligned} F &= U-TS\\ &= U^0(V) + U^V(T,V) - TS\\ & = F^0 + F^V\left\{\begin{aligned} & F^0 = U^0(V)\\ & F^V = U^V(T,V)-TS\\ \end{aligned} \right. \end{aligned}\tag{53}$

其中 $F_V$ 与系统分配分函数有如下关系：

$F^V = -k_BT \mathrm{ln} Z^V\tag{54}$

单谐振子的配分函数为：

$Z_{\bm{q}s}^V = \sum_{n_{qs}=0}^{\infty} e^{-(n_{\bm{q}s}+\frac{1}{2})\hbar\omega_{\bm{q}s}/k_BT} = \frac{e^{-\frac{1}{2}\hbar\omega_{\bm{q}s}/k_BT}}{1-e^{-\hbar\omega_{\bm{q}s}/k_BT}}\tag{55}$

系统总的配分函数为：

$Z^V = \prod_{\bm{q}s} \frac{e^{-\frac{1}{2}\hbar\omega_{\bm{q}s}/k_BT}}{1-e^{-\hbar\omega_{\bm{q}s}/k_BT}}\tag{56}$

$(56)$ 代入 $(54)$ ，得到系统的自由能为：

$\begin{aligned} F^V &= -k_BT\mathrm{ln}\prod_{\bm{q}s} \frac{e^{-\frac{1}{2}\hbar\omega_{\bm{q}s}/k_BT}}{1-e^{-\hbar\omega_{\bm{q}s}/k_BT}}\\ &= k_BT\sum_{\bm{q}s} \{\frac{\hbar\omega_{\bm{q}s}}{2k_BT} + \mathrm{ln}(1-e^{-\hbar\omega_{\bm{q}s}/k_BT}) \}\\ & = k_BT\int_{0}^{\infty} \rho(\omega) [\frac{\hbar\omega}{2k_BT} + \mathrm{ln}(1-e^{-\hbar\omega/k_BT})]d\omega\\ \end{aligned}\tag{57}$

我们注意到， $F^V$ 虽然没有显含 $V$ ，但 $\omega_{\bm{q}s}$ 是与晶体体积有关系的，利用如下公式可以得到压强：

$\begin{aligned} p &= -(\frac{\partial F}{\partial V})|_T\\ &= -\frac{dU^0}{dV} - \sum_{\bm{q}s} \{\frac{1}{2}\hbar + \frac{\hbar e^{-\hbar\omega_{\bm{q}s}/k_BT}}{1-e^{-\hbar\omega_{\bm{q}s}/k_BT}}\}\frac{d\omega_{\bm{q}s}}{dV}\\ &=-\frac{dU^0}{dV} - \sum_{\bm{q}s} \{\frac{1}{2}\hbar\omega_{\bm{q}s} + \frac{\hbar\omega_{\bm{q}s} e^{-\hbar\omega_{\bm{q}s}/k_BT}}{1-e^{-\hbar\omega_{\bm{q}s}/k_BT}}\}\frac{1}{V}\frac{d\ln \omega_{\bm{q}s}}{d\ln V}\\ & = -\frac{dU^0}{dV} + \frac{1}{V}(-\frac{d\ln \omega}{d\ln V})\bar{E} \end{aligned}\tag{58}$

在上式倒数第二步到最后一步中，若考虑各种不同的 $\omega_{\bm{q}s}$ 对 $V$ 的依赖关系不同，这样问题的解是很复杂的。Gruneisen 假定，所有的 $\omega$ 对 $V$ 的依赖关系都相同，并且定义 Gruneisen 常数：

$\gamma = -\frac{d\ln \omega}{d \ln V}\tag{59}$

$\gamma$ 随着 $\omega$ 的增大而变小， $\gamma>0$ ，一般来说 $\gamma$ 在 $1\sim3$ 的范围内。

于是 $(58)$ 可写为：

$p = -\frac{dU^0}{dV} + \gamma\frac{\bar{E}}{V} \tag{60}$

$-\frac{dU^0}{dV}$ 为 内压强，与温度无关
起因于原子间的相互作用。
$\gamma \frac{\bar{E}}{V}$ 为 热压强，是与晶格振动有关的压强。
在温度足够高时，有：

$p^s_{thermal} = \gamma \frac{3Nk_BT}{V_s}$

对比理想气体：

$p^{g}_{internal} = 0$

$p^s_{thermal} V^g = Nk_BT$

得到：

$p^s_{thermal} = 3\gamma p_{thermal}^g \frac{V_g}{V_s}$

假定气体压强为一个大气压，固体约为一千个大气压。

晶格热膨胀

由 $(60)$ 可以得到：

$(\frac{\partial p}{\partial T})_V V= \gamma (\frac{\partial \bar{E}}{\partial T})_V = \gamma C_V \tag{61}$

考虑热膨胀系数与格林奈森系数的关系：

$\begin{aligned} \alpha &= \frac{1}{V}(\frac{\partial V}{\partial T})_p \\ & = -\frac{1}{V}(\frac{\partial V}{\partial p})_T(\frac{\partial p}{\partial T})_V\\ & =\frac{1}{V} \frac{-V(\frac{\partial p}{\partial T})_V}{V(\frac{\partial p}{\partial V})_T}\\ & = \gamma \frac{C_V}{\kappa V} \\ \end{aligned}$