能带理论是目前研究固体中电子运动的一个主要理论基础。作为能带理论的铺垫,我们先介绍经典的 Drude模型。
以解释电子在物质(特别是金属)中的输运性质,Drude 在 1900 年提出了 Drude 模型 [ 1 ] ^{[1]} [ 1 ]
忽略电子与电子之间的相互作用(独立电子近似)
忽略电子与离子之间的相互作用(自由电子近似)
电子只受到均匀外场的作用(平均场)
电子在单位时间内散射的几率为 1 / τ 1/\tau 1 / τ τ \tau τ 电子弛豫时间
电子在各种散射下达到热力学平衡,即电子在碰撞之后的状态是随机的,由热力学平衡决定其分布。
电子的 平均自由程 指的是电子在两次散射之间经过的平均长度。
l = ν ˉ τ l = \bar{\nu}\tau
l = ν ˉ τ
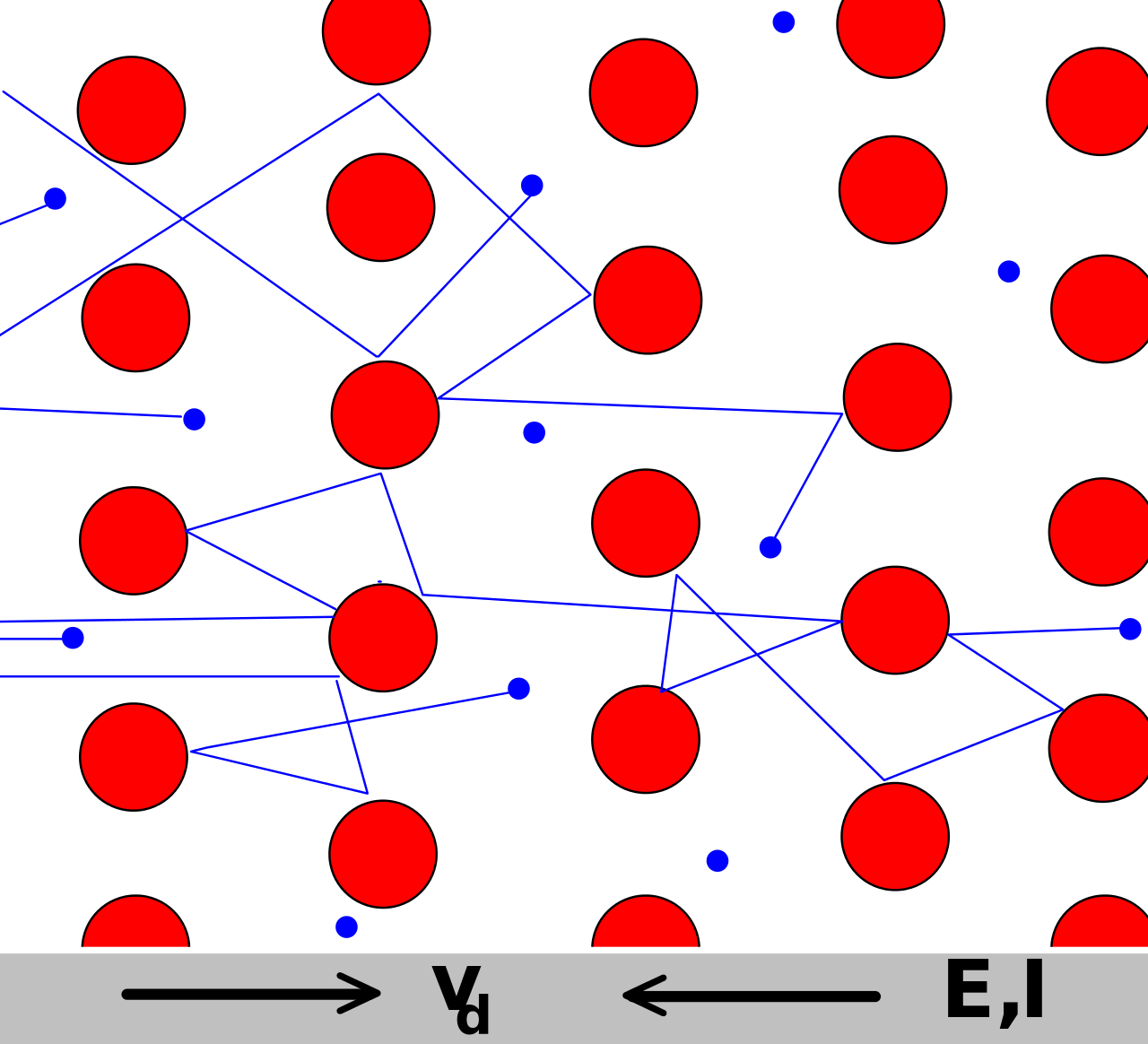
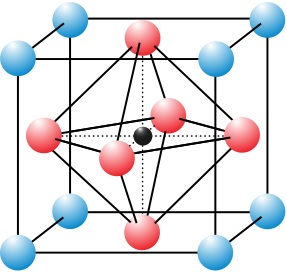
Fig:Drude 模型中的电子(蓝色)不断在较重的、静止的晶体离子中间(红色)徘徊[ 2 ] ^{[2]} [ 2 ]
Drude 模型给出了以下结果:
d d t p ( t ) = q E − p ( t ) τ (1) \frac{d}{dt}\bm{p}(t) = q\bm{E} - \frac{\bm{p}(t)}{\tau} \tag{1}
d t d p ( t ) = q E − τ p ( t ) ( 1 )
电流密度 J \bm{J} J E \bm{E} E
J = ( n q 2 τ m ) E (2) \bm{J} = (\frac{nq^2\tau}{m})\bm{E} \tag{2}
J = ( m n q 2 τ ) E ( 2 )
其中 n n n
Drude 模型使用半定量的语言说明了欧姆定律的正确性。另外,Drude 模型提供了金属中的直流电和交流电传导、霍尔效应,以及热传导非常好的解释。但是在霍尔效应中,Drude 模型并不能预测正电荷载流子的存在(虽然能够应用于正电荷的情况)。
将 Drude 模型进行推广,可以得到其他的模型:
经典力学 → \rightarrow →
自由电子近似 → \rightarrow →
独立电子近似 → \rightarrow →
电子气的局域热平衡 → \rightarrow →
能带理论是一个近似的理论,在固体中存在着大量的电子,它们之间的运动是相互关联着的,每个电子的运动都要受到其他电子运动的影响,该系统的严格解是不可能得到的。相比与 Drude 模型,能带理论首先以量子力学为基础,采用如下近似:
若考虑离子实在平衡位置附近振动,这实际上为模型引入了声子,声子电子可能存在相互作用。
V ( r ) = V ( r + R n ) (3) V(\bm{r}) = V(\bm{r}+\bm{R}_n) \tag{3}
V ( r ) = V ( r + R n ) ( 3 )
其中 R n \bm{R}_n R n
[ − ℏ 2 2 m ∇ 2 + V ( r ) ] ψ = E ψ (4) [-\frac{\hbar^2}{2m}\nabla^2 + V(\bm{r}) ]\psi = E\psi \tag{4}
[ − 2 m ℏ 2 ∇ 2 + V ( r ) ] ψ = E ψ ( 4 )
对于有限体积的晶体可以使用 BK 条件处理。能带理论实际上就是 求解一个周期性势场当中的单电子问题 。
首先,我们从晶格的平移对称性出发,来讨论周期场中单电子的普遍规律。
现在讨论周期性势场中电子波函数的普遍形式。对于周期势场,我们讨论的基础为:平移不变性。
氢原子 ψ ( r ) = ψ n m l ( r , θ , φ ) = R n l ( r ) Y l m ( θ , φ ) \psi(\bm{r}) = \psi_{nml}(r,\theta,\varphi) = R_{nl}(r)Y_{lm}(\theta,\varphi) ψ ( r ) = ψ n m l ( r , θ , φ ) = R n l ( r ) Y l m ( θ , φ ) n n n H ^ \hat{H} H ^ E n = Z e 2 2 a 0 1 n 2 E_n = \frac{Ze^2}{2a_0}\frac{1}{n^2} E n = 2 a 0 Z e 2 n 2 1 主量子数 。l l l L ^ 2 \hat{L}^2 L ^ 2 L 2 = l ( l + 1 ) ℏ 2 L^2 = l(l+1)\hbar^2 L 2 = l ( l + 1 ) ℏ 2 角量子数 。n n n L ^ \hat{L} L ^ L z = m ℏ L_z = m\hbar L z = m ℏ 磁量子数 。n , m , l n,m,l n , m , l
对于自由电子来说,p ^ = ℏ i ∇ ⇒ p = ℏ k \bm{\hat{p}} = \frac{\hbar}{i}\nabla \Rightarrow \bm{p} = \hbar \bm{k} p ^ = i ℏ ∇ ⇒ p = ℏ k
哈密顿算子为:
H ^ = − ℏ 2 2 m ∇ 2 + V ˉ \hat{H} = -\frac{\hbar^2}{2m}\nabla^2 + \bar{V}
H ^ = − 2 m ℏ 2 ∇ 2 + V ˉ
此时有如下对易关系:
[ H ^ , p ^ ] = 0 [\hat{H},\hat{p}] = 0
[ H ^ , p ^ ] = 0
波函数为平面波:
ψ k = 1 L e i k ⋅ r \psi_{\bm{k}} = \frac{1}{\sqrt{L}} e^{i\bm{k}\cdot\bm{r}}
ψ k = L 1 e i k ⋅ r
现在我们考虑如何在引入周期势后,计算电子的波函数。
对于周期场中运动的电子,有哈密顿算子为:
H ^ = − ℏ 2 2 m ∇ 2 + V ( r ) \hat{H} = -\frac{\hbar^2}{2m}\nabla^2 + V(\bm{r})
H ^ = − 2 m ℏ 2 ∇ 2 + V ( r )
周期场具有以下特征:
V ( r ) = V ( r + R m ) V(\bm{r}) = V(\bm{r}+\bm{R_m})
V ( r ) = V ( r + R m )
为了讨论平移对称性,我们需要引入平移算子:
T ^ ( a 1 ) , T ^ ( a 2 ) , T ^ ( a 3 ) \hat{T}(\bm{a}_1)
,\hat{T}(\bm{a}_2)
,\hat{T}(\bm{a}_3)
T ^ ( a 1 ) , T ^ ( a 2 ) , T ^ ( a 3 )
分别对应沿三个基矢 a 1 , a 2 , a 3 \bm{a}_1,\bm{a}_2,\bm{a}_3 a 1 , a 2 , a 3
T ^ ( a i ) φ ( r ) = φ ( r + a i ) \hat{T}(\bm{a}_i)\varphi(\bm{r}) = \varphi(\bm{r}+\bm{a}_i)
T ^ ( a i ) φ ( r ) = φ ( r + a i )
其连续作用 N i N_i N i
T ^ N i ( a i ) φ ( r ) = φ ( r + N i a i ) \hat{T}^{N_i}(\bm{a}_i) \varphi(\bm{r}) =\varphi(\bm{r}+N_i\bm{a}_i)
T ^ N i ( a i ) φ ( r ) = φ ( r + N i a i )
可以得到平移算子之间是对易的:
[ T ^ ( a i ) , T ^ ( a j ) ] = 0 [\hat{T}(\bm{a}_i),\hat{T}(\bm{a}_j)] = 0
[ T ^ ( a i ) , T ^ ( a j ) ] = 0
计算平移算子与哈密顿算子的对易式:
[ H ^ , T ^ ( a i ) ] ψ ( r ) = [ H ^ T ^ ( a i ) − T ^ ( a i ) H ^ ] ψ ( r ) = H ^ T ^ ( a i ) ψ ( r ) − T ^ ( a i ) ( ℏ 2 2 m ∇ 2 + V ( r ) ) ψ ( r ) = H ^ T ^ ( a i ) ψ ( r ) − ( ℏ 2 2 m ∇ r + a i 2 + V ( r + a i ) ) ψ ( r + a i ) = H ^ T ^ ( a i ) ψ ( r ) − ( ℏ 2 2 m ∇ 2 + V ( r ) ) ψ ( r + a i ) = 0 \begin{aligned}
[\hat{H},\hat{T}(\bm{a}_i)] \psi(\bm{r}) &= [\hat{H}\hat{T}(\bm{a}_i)-\hat{T}(\bm{a}_i)\hat{H}]\psi(\bm{r}) \\
& = \hat{H}\hat{T}(\bm{a}_i)\psi(\bm{r}) - \hat{T}( \bm{a}_i )( \frac{\hbar^2}{2m}\nabla^2 + V(\bm{r}) ) \psi(\bm{r})\\
& = \hat{H}\hat{T}(\bm{a}_i)\psi(\bm{r}) - ( \frac{\hbar^2}{2m}\nabla^2_{\bm{r}+\bm{a}_i} + V(\bm{r}+\bm{a}_i) ) \psi(\bm{r}+\bm{a}_i)\\
& = \hat{H}\hat{T}(\bm{a}_i)\psi(\bm{r}) - ( \frac{\hbar^2}{2m}\nabla^2 + V(\bm{r}) ) \psi(\bm{r}+\bm{a}_i)\\
& = 0
\end{aligned}
[ H ^ , T ^ ( a i ) ] ψ ( r ) = [ H ^ T ^ ( a i ) − T ^ ( a i ) H ^ ] ψ ( r ) = H ^ T ^ ( a i ) ψ ( r ) − T ^ ( a i ) ( 2 m ℏ 2 ∇ 2 + V ( r ) ) ψ ( r ) = H ^ T ^ ( a i ) ψ ( r ) − ( 2 m ℏ 2 ∇ r + a i 2 + V ( r + a i ) ) ψ ( r + a i ) = H ^ T ^ ( a i ) ψ ( r ) − ( 2 m ℏ 2 ∇ 2 + V ( r ) ) ψ ( r + a i ) = 0
即得到:
[ H ^ , T ^ ( a i ) ] = 0 [\hat{H},\hat{T}(\bm{a}_i)] = 0
[ H ^ , T ^ ( a i ) ] = 0
为了得到平移算符的本征值及其量子数,需要考虑以下本征方程:
T ^ ( a i ) φ ( r ) = λ ( a i ) φ ( r ) \hat{T}(\bm{a}_i)\varphi(\bm{r}) = \lambda(\bm{a}_i) \varphi (\bm{r})
T ^ ( a i ) φ ( r ) = λ ( a i ) φ ( r )
可得
T ^ n ( a i ) φ ( r ) = λ n φ ( r ) \hat{T}^n(\bm{a}_i)\varphi(\bm{r}) = \lambda^n \varphi (\bm{r})
T ^ n ( a i ) φ ( r ) = λ n φ ( r )
考虑 ∣ λ ∣ > 1 |\lambda|>1 ∣ λ ∣ > 1 ∣ λ ∣ < 1 |\lambda|<1 ∣ λ ∣ < 1 φ \varphi φ ∣ λ ∣ = 1 |\lambda| = 1 ∣ λ ∣ = 1
此时得到电子的几率密度为周期函数:
∣ φ ( r + a i ) ∣ 2 = ∣ λ ( a i ) φ ( r ) ∣ 2 = ∣ φ ∣ 2 |\varphi(\bm{r}+\bm{a}_i)|^2 = |\lambda(\bm{a}_i)\varphi(\bm{r})|^2 = |\varphi|^2
∣ φ ( r + a i ) ∣ 2 = ∣ λ ( a i ) φ ( r ) ∣ 2 = ∣ φ ∣ 2
另外容易得到:
λ ( a 1 + a 2 ) = λ ( a 1 ) λ ( a 2 ) \lambda(\bm{a}_1 + \bm{a}_2) = \lambda(\bm{a}_1)\lambda(\bm{a}_2)
λ ( a 1 + a 2 ) = λ ( a 1 ) λ ( a 2 )
可以推测 λ \lambda λ
λ ( a i ) = e i k ⋅ a i \lambda(\bm{a}_i) = e^{i\bm{k}\cdot\bm{a}_i}
λ ( a i ) = e i k ⋅ a i
考虑 BK 条件对 k \bm{k} k
此处 k \bm{k} k
φ ( r + N i a i ) = φ ( r ) \varphi(\bm{r}+N_i\bm{a}_i) = \varphi(\bm{r})
φ ( r + N i a i ) = φ ( r )
得到:
{ N 1 k ⋅ a 1 = 2 π l 1 N 2 k ⋅ a 2 = 2 π l 2 N 3 k ⋅ a 3 = 2 π l 3 ⟹ k = l 1 N 1 b 1 + l 2 N 2 b 2 + l 3 N 3 b 3 \left\{
\begin{aligned}
N_1\bm{k}\cdot\bm{a}_1 = 2\pi l_1\\
N_2\bm{k}\cdot\bm{a}_2 = 2\pi l_2\\
N_3\bm{k}\cdot\bm{a}_3 = 2\pi l_3\\
\end{aligned}
\right.\Longrightarrow \bm{k} = \frac{l_1}{N_1}\bm{b}_1 + \frac{l_2}{N_2}\bm{b}_2 + \frac{l_3}{N_3}\bm{b}_3
⎩ ⎪ ⎨ ⎪ ⎧ N 1 k ⋅ a 1 = 2 π l 1 N 2 k ⋅ a 2 = 2 π l 2 N 3 k ⋅ a 3 = 2 π l 3 ⟹ k = N 1 l 1 b 1 + N 2 l 2 b 2 + N 3 l 3 b 3
三个方向的平移算子对应的量子数就为:
{ k 1 = l 1 N 1 , l 1 = 0 , 1 , ⋯ , N 1 − 1 k 2 = l 2 N 2 , l 2 = 0 , 1 , ⋯ , N 2 − 1 k 3 = l 3 N 3 , l 3 = 0 , 1 , ⋯ , N 3 − 1 (5) \left\{
\begin{aligned}
k_1 = \frac{l_1}{N_1},\quad l_1 = 0,1,\cdots,N_1-1\\
k_2 = \frac{l_2}{N_2},\quad l_2 = 0,1,\cdots,N_2-1\\
k_3 = \frac{l_3}{N_3},\quad l_3 = 0,1,\cdots,N_3-1\\
\end{aligned}\tag{5}
\right.
⎩ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎧ k 1 = N 1 l 1 , l 1 = 0 , 1 , ⋯ , N 1 − 1 k 2 = N 2 l 2 , l 2 = 0 , 1 , ⋯ , N 2 − 1 k 3 = N 3 l 3 , l 3 = 0 , 1 , ⋯ , N 3 − 1 ( 5 )
周期场中电子状态可以用平移算子和哈密顿算子对应的量子数 k \bm{k} k n n n ψ n k ( r ) \psi_{n\bm{k}}(\bm{r}) ψ n k ( r )
Bloch 定理 R m \bm{R}_m R m e i k ⋅ R m e^{i\bm{k}\cdot\bm{R_m}} e i k ⋅ R m
Bloch 波
根据 Bloch 定理:
ψ n k ( r ) = e i k ⋅ r u n k ( r ) (6) \psi_{n\bm{k}}(\bm{r}) = e^{i\bm{k}\cdot\bm{r}} u_{n\bm{k}}(\bm{r}) \tag{6}
ψ n k ( r ) = e i k ⋅ r u n k ( r ) ( 6 )
其形式就为调幅平面波,其中 u n k ( r ) u_{n\bm{k}}(\bm{r}) u n k ( r ) Bloch 函数 。
Bloch 波的能谱特性 k \bm{k} k E n ( k ) E^n(\bm{k}) E n ( k ) ψ k n ( x ) \psi_{\bm{k}n}(\bm{x}) ψ k n ( x )
考虑能量本征方程为:
[ − ℏ 2 2 m ∇ 2 + V ( r ) ] e i k ⋅ r u k n ( r ) = E n ( k ) e i k ⋅ r u k n ( r ) [-\frac{\hbar^2}{2m}\nabla^2 + V(\bm{r})] e^{i\bm{k}\cdot\bm{r}} u_{\bm{k}n}(\bm{r}) = E_n(\bm{k}) e^{i\bm{k}\cdot\bm{r}} u_{\bm{k}n}(\bm{r})
[ − 2 m ℏ 2 ∇ 2 + V ( r ) ] e i k ⋅ r u k n ( r ) = E n ( k ) e i k ⋅ r u k n ( r )
两边同时乘以因子 e − i k ⋅ r e^{-i\bm{k}\cdot\bm{r}} e − i k ⋅ r
H ^ k u k n ( r ) = E n ( k ) u k n ( r ) \hat{H}_{\bm{k}} u_{\bm{k}n}(\bm{r}) = E_n(\bm{k})u_{\bm{k}n}(\bm{r})
H ^ k u k n ( r ) = E n ( k ) u k n ( r )
属于有限区域内本征值问题。S t u r n − L i o n v i l l e Sturn-Lionville S t u r n − L i o n v i l l e n n n E n ( k ) E_n(\bm{k}) E n ( k ) k \bm{k} k
首先讨论最简单的一维模型。所谓 NFC近似 ,又称 近自由电子近似 ,其假定周期场的起伏比较小。相比于平均场 V ˉ \bar{V} V ˉ V ( x ) − V ˉ V(x)-\bar{V} V ( x ) − V ˉ
对于正格子上的周期函数可以使用倒格矢展开:
V ( x ) = V ( x + n a ) = ∑ V n e i 2 π n a x (7) \begin{aligned}
V(x) &= V(x+na)\\
& = \sum V_n e^{i\frac{2\pi n}{a}x}\\
\end{aligned}\tag{7}
V ( x ) = V ( x + n a ) = ∑ V n e i a 2 π n x ( 7 )
其中:
V n = 1 a ∫ 0 a V ( ξ ) e − i 2 π n a ξ d ξ (8) V_n = \frac{1}{a}\int_0^a V(\xi)e^{-i\frac{2\pi n}{a}\xi}d\xi\tag{8}
V n = a 1 ∫ 0 a V ( ξ ) e − i a 2 π n ξ d ξ ( 8 )
n = 0 n=0 n = 0 V ˉ \bar{V} V ˉ
V ˉ = 1 a ∫ 0 a V ( ξ ) d ξ (9) \bar{V} = \frac{1}{a}\int_{0}^{a} V(\xi)d\xi \tag{9}
V ˉ = a 1 ∫ 0 a V ( ξ ) d ξ ( 9 )
综上可得:
V ( x ) = V ˉ + ∑ ′ V n e i 2 π n a ξ = V ˉ + Δ V (10) V(x) = \bar{V} +\sum' V_n e^{i\frac{2\pi n}{a}\xi} =\bar{V} + \Delta V \tag{10}
V ( x ) = V ˉ + ∑ ′ V n e i a 2 π n ξ = V ˉ + Δ V ( 1 0 )
∑ ′ \sum' ∑ ′
平均场作为零级近似,其波动方程为:
− ℏ 2 2 m d 2 d x 2 ψ 0 + V ˉ ψ 0 = E 0 ψ 0 (11) -\frac{\hbar^2}{2m}\frac{d^2}{dx^2}\psi^0 + \bar{V}\psi^0 = E^0\psi^0 \tag{11}
− 2 m ℏ 2 d x 2 d 2 ψ 0 + V ˉ ψ 0 = E 0 ψ 0 ( 1 1 )
其解为恒定场 V ˉ \bar{V} V ˉ
ψ k 0 ( x ) = 1 L e i k x , E k 0 = ℏ 2 k 2 2 m + V ˉ (12) \psi_k^0(x) = \frac{1}{\sqrt{L}} e^{ikx},\quad E_k^0= \frac{\hbar^2k^2}{2m} + \bar{V} \tag{12}
ψ k 0 ( x ) = L 1 e i k x , E k 0 = 2 m ℏ 2 k 2 + V ˉ ( 1 2 )
此处 L = N a L = Na L = N a
若引入 BK 条件,则 k k k
k = l N a ( 2 π ) , l ∈ Z (13) k = \frac{l}{Na}(2\pi),\quad l \in \mathbb{Z} \tag{13}
k = N a l ( 2 π ) , l ∈ Z ( 1 3 )
k k k
容易验证波函数满足正交归一化条件:
∫ 0 N a ψ k ′ 0 ψ k 0 = δ k k ′ (14) \int_{0}^{Na} \psi_{k'}^0 \psi_k^0 = \delta_{kk'} \tag{14}
∫ 0 N a ψ k ′ 0 ψ k 0 = δ k k ′ ( 1 4 )
将 Δ V \Delta V Δ V
首先考虑非简并微扰,能量的一级修正为
E k ( 1 ) = ⟨ k ∣ Δ V ∣ k ⟩ = ∫ ∣ ψ k 0 ∣ 2 ( V ( x ) − V ˉ ) d x = 0 (15) \begin{aligned}
E_k^{(1)} &= \langle k|\Delta V|k\rangle\\
& = \int |\psi_k^0|^2 (V(x)-\bar{V}) dx = 0\\
\end{aligned}\tag{15}
E k ( 1 ) = ⟨ k ∣ Δ V ∣ k ⟩ = ∫ ∣ ψ k 0 ∣ 2 ( V ( x ) − V ˉ ) d x = 0 ( 1 5 )
继续考虑二阶修正:
E k ( 2 ) = ∑ k ′ ∣ ⟨ k ′ ∣ Δ V ∣ k ⟩ ∣ 2 E k 0 − E k ′ 0 = ∑ k ′ ∣ ⟨ k ′ ∣ Δ V ∣ k ⟩ ∣ 2 E k 0 − E k ′ 0 = ∑ k ′ ∣ ⟨ k ′ ∣ V ( x ) ∣ k ⟩ ∣ 2 E k 0 − E k ′ 0 (16) \begin{aligned}
E_k^{(2)} &= \sum_{k'} \frac{|\langle k'|\Delta V|k\rangle|^2}{E_k^0 - E^0_{k'}} \\
& = \sum_{k'} \frac{|\langle k'|\Delta V|k\rangle|^2}{E_k^0 - E^0_{k'}}\\
& = \sum_{k'} \frac{|\langle k'|V(x)|k\rangle|^2}{E_k^0 - E^0_{k'}}\\
\end{aligned}\tag{16}
E k ( 2 ) = k ′ ∑ E k 0 − E k ′ 0 ∣ ⟨ k ′ ∣ Δ V ∣ k ⟩ ∣ 2 = k ′ ∑ E k 0 − E k ′ 0 ∣ ⟨ k ′ ∣ Δ V ∣ k ⟩ ∣ 2 = k ′ ∑ E k 0 − E k ′ 0 ∣ ⟨ k ′ ∣ V ( x ) ∣ k ⟩ ∣ 2 ( 1 6 )
现在计算跃迁矩阵元 ⟨ k ′ ∣ V ( x ) ∣ k ⟩ \langle k'|V(x)|k\rangle ⟨ k ′ ∣ V ( x ) ∣ k ⟩
⟨ k ′ ∣ V ( x ) ∣ k ⟩ = 1 N a ∫ 0 N a e − i ( k ′ − k ) x V ( x ) d x = 1 N a ∑ n = 0 N − 1 ∫ n a ( n + 1 ) a e − i ( k ′ − k ) x V ( x ) d x = x = ξ + n a 1 N a ∑ n = 0 N − 1 e i ( k − k ′ ) n a ∫ 0 a e − i ( k ′ − k ) ξ V ( ξ ) d ξ = 1 a δ k ′ , k + 2 π n a ∫ 0 a e − i ( k ′ − k ) ξ V ( ξ ) d ξ = 1 a δ k ′ , k + 2 π n a 1 a ∫ 0 a e − i 2 π n ξ a V ( ξ ) d ξ = δ k ′ , k + 2 π n a V n (17) \begin{aligned}
\langle k'| V(x) |k\rangle &= \frac{1}{Na} \int_{0}^{Na} e^{-i(k'-k)x} V(x)dx\\ \\
&=\frac{1}{Na} \sum_{n=0}^{N-1} \int_{na}^{(n+1)a} e^{-i(k'-k)x} V(x)dx\\
& \overset{x = \xi + na}{ = } \frac{1}{Na} \sum_{n=0}^{N-1} e^{i(k-k')na} \int_{0}^{a} e^{-i(k'-k)\xi} V(\xi) d\xi \\
& = \frac{1}{a}\delta_{k',k+\frac{2\pi n}{a}} \int_{0}^{a} e^{-i(k'-k)\xi} V(\xi) d\xi \\
& = \frac{1}{a}\delta_{k',k+\frac{2\pi n}{a}} \frac{1}{a}\int_{0}^{a} e^{-i\frac{2\pi n\xi}{a}} V(\xi) d\xi \\
& = \delta_{k',k+\frac{2\pi n}{a}}V_{n} \tag{17}
\end{aligned}
⟨ k ′ ∣ V ( x ) ∣ k ⟩ = N a 1 ∫ 0 N a e − i ( k ′ − k ) x V ( x ) d x = N a 1 n = 0 ∑ N − 1 ∫ n a ( n + 1 ) a e − i ( k ′ − k ) x V ( x ) d x = x = ξ + n a N a 1 n = 0 ∑ N − 1 e i ( k − k ′ ) n a ∫ 0 a e − i ( k ′ − k ) ξ V ( ξ ) d ξ = a 1 δ k ′ , k + a 2 π n ∫ 0 a e − i ( k ′ − k ) ξ V ( ξ ) d ξ = a 1 δ k ′ , k + a 2 π n a 1 ∫ 0 a e − i a 2 π n ξ V ( ξ ) d ξ = δ k ′ , k + a 2 π n V n ( 1 7 )
由此得到能量的二阶修正项为:
E k ( 2 ) = ∑ k ′ ∣ ⟨ k ′ ∣ Δ V ∣ k ⟩ ∣ 2 E k 0 − E k ′ 0 = ∑ k ′ δ k ′ , k + 2 π n a ∣ V n ∣ 2 E k 0 − E k ′ 0 = ∑ n ℏ 2 k 4 2 m [ k 2 − ( k + 2 π n a ) 2 ] (18) \begin{aligned}
E_k^{(2)} &= \sum_{k'} \frac{|\langle k'|\Delta V|k\rangle|^2}{E_k^0 - E^0_{k'}}\\
&= \sum_{k'} \delta_{k',k+\frac{2\pi n}{a}} \frac{|V_{n}|^2}{E^0_k-E^0_{k'}}\\
&= \sum_{n} \frac{\hbar^2 k^4}{2m[k^2 - (k+\frac{2\pi n}{a})^2]}\\
\end{aligned}\tag{18}
E k ( 2 ) = k ′ ∑ E k 0 − E k ′ 0 ∣ ⟨ k ′ ∣ Δ V ∣ k ⟩ ∣ 2 = k ′ ∑ δ k ′ , k + a 2 π n E k 0 − E k ′ 0 ∣ V n ∣ 2 = n ∑ 2 m [ k 2 − ( k + a 2 π n ) 2 ] ℏ 2 k 4 ( 1 8 )
考虑波函数的一阶微扰,得到修正后的波函数:
ψ k = ψ k 0 + ∑ k ′ ⟨ k ′ ∣ Δ V ∣ k ⟩ E k 0 − E k ′ 0 ψ k ′ 0 = ψ k 0 + ∑ k ′ ⟨ k ′ ∣ V ( x ) ∣ k ⟩ E k 0 − E k ′ 0 ψ k ′ 0 = ψ k 0 + ∑ k ′ δ k ′ , k + 2 π n a V n E k 0 − E k ′ 0 ψ k ′ 0 = 1 L e i k x + ∑ n 2 m V n ℏ 2 ( k 2 − ( k + 2 π n a ) 2 ) 1 L e i ( k + 2 π n a ) x = 1 L e i k x ( 1 + ∑ n 2 m V n ℏ 2 ( k 2 − ( k + 2 π n a ) 2 ) e i 2 π n a x ) (19) \begin{aligned}
\psi_k &= \psi_k^0 + \sum_{k'}\frac{\langle k'|\Delta V|k\rangle}{E_k^0-E_{k'}^0}\psi_{k'}^0\\
&= \psi_k^0 + \sum_{k'}\frac{\langle k'|V(x)|k\rangle}{E_k^0-E_{k'}^0}\psi_{k'}^0\\
&= \psi_k^0 + \sum_{k'}\frac{ \delta_{k',k+\frac{2\pi n}{a}} V_{n}}{E_k^0-E_{k'}^0}\psi_{k'}^0\\
&= \frac{1}{\sqrt{L}} e^{ikx} + \sum_{n}\frac{2mV_{n}}{\hbar^2(k^2-(k+\frac{2\pi n}{a})^2)}\frac{1}{\sqrt{L}} e^{i(k+\frac{2\pi n}{a})x}\\
&= \frac{1}{\sqrt{L}} e^{ikx}(1+\sum_{n}\frac{2mV_{n}}{\hbar^2(k^2-(k+\frac{2\pi n}{a})^2)}e^{i\frac{2\pi n}{a}x})
\end{aligned}\tag{19}
ψ k = ψ k 0 + k ′ ∑ E k 0 − E k ′ 0 ⟨ k ′ ∣ Δ V ∣ k ⟩ ψ k ′ 0 = ψ k 0 + k ′ ∑ E k 0 − E k ′ 0 ⟨ k ′ ∣ V ( x ) ∣ k ⟩ ψ k ′ 0 = ψ k 0 + k ′ ∑ E k 0 − E k ′ 0 δ k ′ , k + a 2 π n V n ψ k ′ 0 = L 1 e i k x + n ∑ ℏ 2 ( k 2 − ( k + a 2 π n ) 2 ) 2 m V n L 1 e i ( k + a 2 π n ) x = L 1 e i k x ( 1 + n ∑ ℏ 2 ( k 2 − ( k + a 2 π n ) 2 ) 2 m V n e i a 2 π n x ) ( 1 9 )
这表示考虑一阶修正后的波函数是一个调幅的平面波,并且调幅因子由上式给出。我们考虑一个特殊的波矢:
k = − π n a (20) k = -\frac{\pi n}{a} \tag{20}
k = − a π n ( 2 0 )
此时我们得到能量的二阶修正、修正后的波函数均是发散的。这是因为此时 k = − π n a k = -\frac{\pi n}{a} k = − a π n k ′ = π n a k' = \frac{\pi n}{a} k ′ = a π n k = − π n a k = -\frac{\pi n}{a} k = − a π n
此时的波函数应当为简并的零阶波函数的线性叠加:
ψ = a ψ k 0 + b ψ k ′ 0 (21) \psi = a\psi_k^0 + b\psi_{k'}^0 \tag{21}
ψ = a ψ k 0 + b ψ k ′ 0 ( 2 1 )
其满足如下波动方程:
− ℏ 2 2 m d 2 d x 2 ψ k 0 + V ˉ ψ k 0 = E k 0 ψ k 0 − ℏ 2 2 m d 2 d x 2 ψ k ′ 0 + V ˉ ψ k ′ 0 = E k ′ 0 ψ k ′ 0 − ℏ 2 2 m d 2 d x 2 ψ k + V ( x ) ψ k = E ψ k (22) \begin{aligned}
&-\frac{\hbar^2}{2m}\frac{d^2}{dx^2}\psi^0_k + \bar{V}\psi^0_k = E^0_k \psi^0_k\\
&-\frac{\hbar^2}{2m}\frac{d^2}{dx^2}\psi^0_{k'} + \bar{V}\psi^0_{k'} = E^0_{k'} \psi^0_{k'}\\
&-\frac{\hbar^2}{2m}\frac{d^2}{dx^2}\psi_k +V(x)\psi_k = E\psi_k\\
\end{aligned}\tag{22}
− 2 m ℏ 2 d x 2 d 2 ψ k 0 + V ˉ ψ k 0 = E k 0 ψ k 0 − 2 m ℏ 2 d x 2 d 2 ψ k ′ 0 + V ˉ ψ k ′ 0 = E k ′ 0 ψ k ′ 0 − 2 m ℏ 2 d x 2 d 2 ψ k + V ( x ) ψ k = E ψ k ( 2 2 )
得到:
a ( E k 0 − E + Δ V ) ψ k 0 + b ( E k ′ 0 − E + Δ V ) ψ k ′ 0 = 0 (23) a(E_k^0 -E + \Delta V)\psi^0_k + b(E_{k'}^0 -E +\Delta V)\psi^0_{k'} = 0\tag{23}
a ( E k 0 − E + Δ V ) ψ k 0 + b ( E k ′ 0 − E + Δ V ) ψ k ′ 0 = 0 ( 2 3 )
此时利用正交关系,分别左乘 ψ k ∗ ( x ) , ψ k ′ ∗ ( x ) \psi_k^*(x),\psi_{k'}^*(x) ψ k ∗ ( x ) , ψ k ′ ∗ ( x )
{ a ( E k 0 − E ) + b V n ∗ = 0 a V n + b ( E k ′ 0 − E ) = 0 (24) \left\{
\begin{aligned}
& a (E_k^0-E) + b V_n^* = 0\\
& a V_n + b (E_{k'}^0-E) = 0\\
\end{aligned}
\right.\tag{24}
{ a ( E k 0 − E ) + b V n ∗ = 0 a V n + b ( E k ′ 0 − E ) = 0 ( 2 4 )
若以上方程存在非零解,那么有:
∣ E k 0 − E V n ∗ V n E k ′ 0 − E ∣ = ( E k 0 − E ) ( E k ′ 0 − E ) − ∣ V n ∣ 2 = 0 (25) \begin{vmatrix}
E_k^0-E & V_n^* \\
V_n & E_{k'}^0-E\\
\end{vmatrix} = (E_k^0-E)(E_{k'}^0-E)-|V_n|^2 = 0 \tag{25}
∣ ∣ ∣ ∣ E k 0 − E V n V n ∗ E k ′ 0 − E ∣ ∣ ∣ ∣ = ( E k 0 − E ) ( E k ′ 0 − E ) − ∣ V n ∣ 2 = 0 ( 2 5 )
对应有:
E ± = 1 2 { E k 0 + E k ′ 0 ± ( E k 0 − E k ′ 0 ) 2 + 4 ∣ V n ∣ 2 } (26) E_{\pm} = \frac{1}{2}\{E_k^0 + E_{k'}^0 \pm \sqrt{ (E_k^0-E_{k'}^0)^2 + 4|V_n|^2 }\} \tag{26}
E ± = 2 1 { E k 0 + E k ′ 0 ± ( E k 0 − E k ′ 0 ) 2 + 4 ∣ V n ∣ 2 } ( 2 6 )
考虑到 E k 0 = E k ′ 0 = ℏ 2 k 2 2 m E_k^0=E_{k'}^0 = \frac{\hbar^2k^2}{2m} E k 0 = E k ′ 0 = 2 m ℏ 2 k 2 ( 26 (26 ( 2 6
E ± = ℏ 2 k 2 2 m ± ∣ V n ∣ (27) E_{\pm} = \frac{\hbar^2k^2}{2m} \pm |V_n| \tag{27}
E ± = 2 m ℏ 2 k 2 ± ∣ V n ∣ ( 2 7 )
我们发现,考虑简并微扰之后,能级发生了分裂。在布里渊区的边界处,能量发生了突变(之后会详细讨论)。
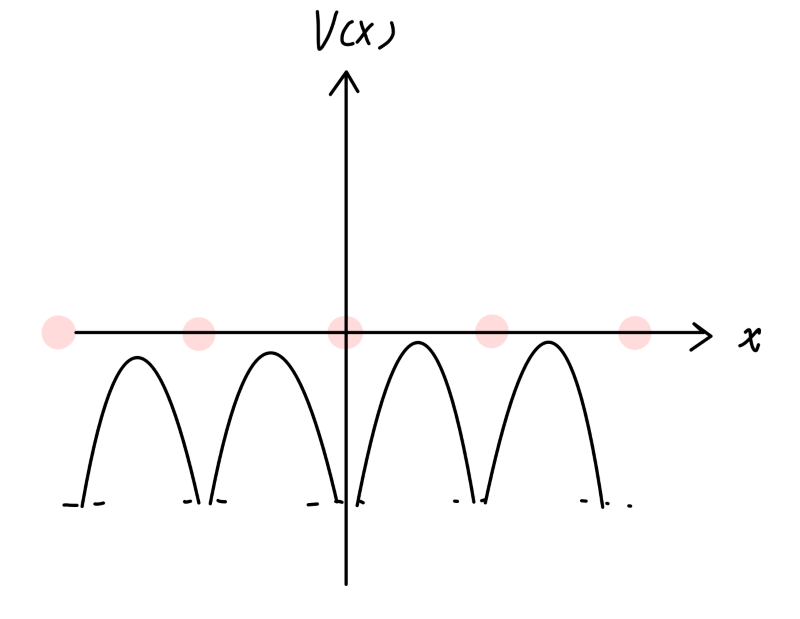
一维链的周期势大概如图所示(其中粉色代表离子实)。
Fig:一维链的周期势
这种情况下,离子实附近势能较低,可以认为 V n V_n V n
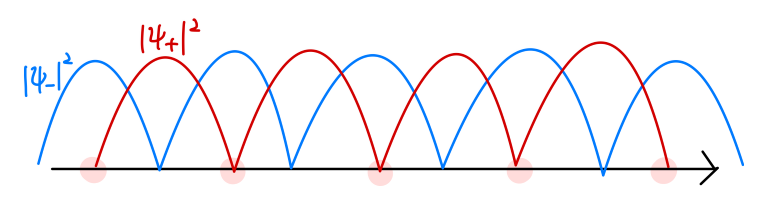
{ ψ − = 1 2 ( ψ k 0 + ψ k ′ 0 ) = 2 L cos n π a ψ + = 1 2 ( ψ k 0 − ψ k ′ 0 ) = − 2 L i sin n π a (28) \left\{
\begin{aligned}
& \psi_{-} = \frac{1}{\sqrt{2}} (\psi_k^0 + \psi_{k'}^0) = \sqrt{\frac{2}{L}} \cos \frac{n\pi}{a} \\
& \psi_{+} = \frac{1}{\sqrt{2}} (\psi_k^0 - \psi_{k'}^0) = - \sqrt{\frac{2}{L}} i \sin \frac{n\pi}{a} \\
\end{aligned} \tag{28}
\right.
⎩ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎧ ψ − = 2 1 ( ψ k 0 + ψ k ′ 0 ) = L 2 cos a n π ψ + = 2 1 ( ψ k 0 − ψ k ′ 0 ) = − L 2 i sin a n π ( 2 8 )
我们发现,ψ k 0 \psi^0_{k} ψ k 0 ψ k ′ 0 \psi^0_{k'} ψ k ′ 0
ψ − \psi_{-} ψ − ψ + \psi_{+} ψ +
Fig:布里渊区边界的驻波
在布里渊区边界附近,简并微扰也是近似有效的。现在考虑两种情况:
∣ E k 0 − E k ′ 0 ∣ ≫ ∣ V n ∣ |E^0_k - E^0_{k'}| \gg |V_n| ∣ E k 0 − E k ′ 0 ∣ ≫ ∣ V n ∣
这表示 k k k − n π a -\frac{n\pi}{a} − a n π k ′ k' k ′ ( 26 ) (26) ( 2 6 )
E + = E k ′ 0 + ∣ V n ∣ 2 E k ′ 0 − E k 0 E − = E k 0 − ∣ V n ∣ 2 E k ′ 0 − E k 0 (29) \begin{aligned}
&E_{+} = E_{k'}^0 + \frac{|V_n|^2}{E^0_{k'}-E^0_{k}}\\
&E_{-} = E_{k}^0 - \frac{|V_n|^2}{E^0_{k'}-E^0_{k}}\\
\end{aligned} \tag{29}
E + = E k ′ 0 + E k ′ 0 − E k 0 ∣ V n ∣ 2 E − = E k 0 − E k ′ 0 − E k 0 ∣ V n ∣ 2 ( 2 9 )
不难发现(不妨假设 Δ = E k 0 − E k ′ 0 > 0 \Delta = E^0_{k}-E^0_{k'} > 0 Δ = E k 0 − E k ′ 0 > 0 排斥作用 ”。
∣ E k 0 − E k ′ 0 ∣ ≪ ∣ V n ∣ |E^0_k - E^0_{k'}| \ll |V_n| ∣ E k 0 − E k ′ 0 ∣ ≪ ∣ V n ∣
这表示 k k k − n π a -\frac{n\pi}{a} − a n π
E ± = 1 2 { E k 0 + E k ′ 0 ± [ 2 ∣ V n ∣ + ( E k ′ 0 − E k 0 ) 2 4 ∣ V n ∣ ] } (30) E_{\pm} = \frac{1}{2}\{ E^0_{k} + E^0_{k'} \pm [ 2|V_n| + \frac{(E^0_{k'}-E_{k}^0)^2}{4|V_n|} ] \} \tag{30}
E ± = 2 1 { E k 0 + E k ′ 0 ± [ 2 ∣ V n ∣ + 4 ∣ V n ∣ ( E k ′ 0 − E k 0 ) 2 ] } ( 3 0 )
代入 E k 0 , E k ′ 0 E^0_k,E^0_{k'} E k 0 , E k ′ 0 Δ \Delta Δ
E + = V ˉ + T n + Δ 2 T n ( 2 T n ∣ V n ∣ + 1 ) E − = V ˉ + T n − Δ 2 T n ( 2 T n ∣ V n ∣ − 1 ) (31) \begin{aligned}
E_{+} &= \bar{V} + T_n + \Delta^2 T_n (\frac{2T_n}{|V_n|}+1)\\
E_{-} &= \bar{V} + T_n - \Delta^2 T_n (\frac{2T_n}{|V_n|}-1)\\
\end{aligned} \tag{31}
E + E − = V ˉ + T n + Δ 2 T n ( ∣ V n ∣ 2 T n + 1 ) = V ˉ + T n − Δ 2 T n ( ∣ V n ∣ 2 T n − 1 ) ( 3 1 )
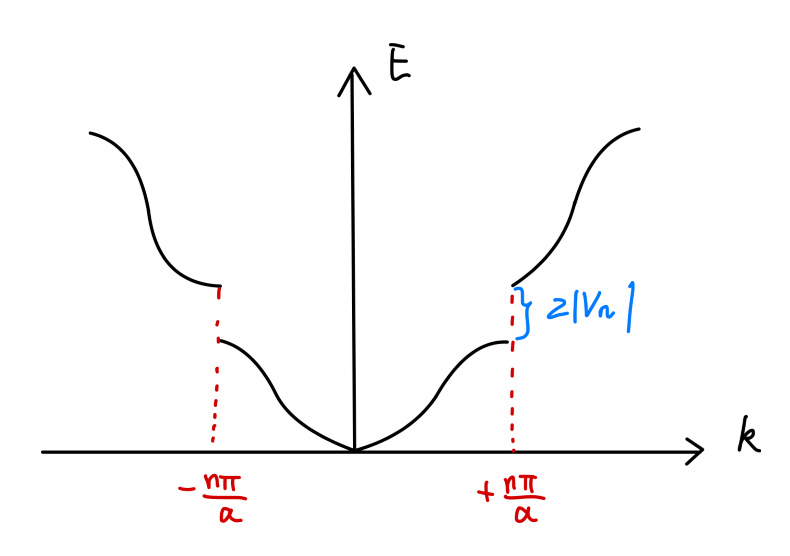
可以得到当 Δ → 0 \Delta\rightarrow 0 Δ → 0 E ± E_{\pm} E ± V ˉ + T n ± ∣ V n ∣ \bar{V}+T_n\pm|V_n| V ˉ + T n ± ∣ V n ∣
Fig:一维链的能带结构
能带与禁带
能隙 :k k k n π a \frac{n\pi}{a} a n π 2 ∣ V n ∣ 2|V_{n}| 2 ∣ V n ∣
一般来说,能量轴上是能量准连续取值的一系列区域。电子状态的波矢取一系列离散值 k = 2 π l N a k = \frac{2\pi l}{Na} k = N a 2 π l N N N k k k k k k V n ≠ 0 V_n \neq 0 V n = 0
带 1 1 1 k ∈ ( − π / a , π / a ) k\in (-\pi/a,\pi/a) k ∈ ( − π / a , π / a )
带 2 2 2 k ∈ ( − 2 π / a , − π / a ) ∪ ( π / a , 2 π / a ) k\in (-2\pi/a,-\pi/a)\cup (\pi/a,2\pi/a) k ∈ ( − 2 π / a , − π / a ) ∪ ( π / a , 2 π / a )
禁带 :在能量轴上每两个能带之间的间隔称为禁带。
禁带是指状态的真空区域,其中没有能级,即不存在禁带中能量对应的量子态。仅在一维情况下,禁带与能隙一一对应。
可以使用与一维情况类似的方法讨论三维的情况。波动方程为:
[ − ℏ 2 2 m ∇ 2 + V ( r ) ] ψ ( r ) = E ψ ( r ) (32) [-\frac{\hbar^2}{2m}\nabla^2 + V(\bm{r})] \psi(\bm{r}) = E\psi(\bm{r}) \tag{32}
[ − 2 m ℏ 2 ∇ 2 + V ( r ) ] ψ ( r ) = E ψ ( r ) ( 3 2 )
其中 V ( r + R m ) V(\bm{r}+\bm{R}_m) V ( r + R m )
V ( r + R m ) = V ( r ) V(\bm{r}+\bm{R}_m) = V(\bm{r})
V ( r + R m ) = V ( r )
其中 R m \bm{R}_m R m
R m = m 1 α 1 + m 2 α 2 + m 3 α 3 \bm{R}_m = m_1\bm{\alpha}_1 + m_2\bm{\alpha}_2 + m_3\bm{\alpha}_3
R m = m 1 α 1 + m 2 α 2 + m 3 α 3
零级近似对应势能取平均场 V ˉ \bar{V} V ˉ
ψ k 0 = 1 V e i k ⋅ r (33) \psi^0_{\bm{k}} = \frac{1}{\sqrt{V}} e^{i\bm{k}\cdot\bm{r}} \tag{33}
ψ k 0 = V 1 e i k ⋅ r ( 3 3 )
对应的能量本征值为:
E k 0 = V ˉ + ℏ 2 k 2 2 m (34) E_{\bm{k}}^0 = \bar{V} + \frac{\hbar^2k^2}{2m} \tag{34}
E k 0 = V ˉ + 2 m ℏ 2 k 2 ( 3 4 )
引入 BK 条件,此时的波矢只能取一系列离散值:
k = l 1 N 1 b 1 + l 2 N 2 b 2 + l 3 N 3 b 3 (34) \bm{k} = \frac{l_1}{N_1}\bm{b}_1 + \frac{l_2}{N_2}\bm{b}_2 + \frac{l_3}{N_3}\bm{b}_3 \tag{34}
k = N 1 l 1 b 1 + N 2 l 2 b 2 + N 3 l 3 b 3 ( 3 4 )
b 1 , b 2 , b 3 \bm{b}_1,\bm{b}_2,\bm{b}_3 b 1 , b 2 , b 3
不难得到,波函数满足正交归一化条件:
∫ ψ k ′ 0 ∗ ψ k 0 d r = δ k ′ k (35) \int \psi_{\bm{k'}}^{0*}\psi_{\bm{k}}^0d\bm{r} = \delta_{\bm{k'}\bm{k}} \tag{35}
∫ ψ k ′ 0 ∗ ψ k 0 d r = δ k ′ k ( 3 5 )
类似的,我们现在直接在布里渊区边界考虑简并微扰。可以计算得到:
⟨ k ′ ∣ V ( r ) ∣ k ⟩ = V n = 1 V ∭ e − i G n ⋅ r V ( r ) d r (36) \begin{aligned}
\langle \bm{k}' | V(\bm{r}) |\bm{k}\rangle &= V_{n}\\
& = \frac{1}{V}\iiint e^{-i\bm{G}_n\cdot\bm{r}}V(\bm{r}) d\bm{r} \\
\end{aligned} \tag{36}
⟨ k ′ ∣ V ( r ) ∣ k ⟩ = V n = V 1 ∭ e − i G n ⋅ r V ( r ) d r ( 3 6 )
n n n ( n 1 , n 2 , n 3 ) (n_1,n_2,n_3) ( n 1 , n 2 , n 3 )
其中 k , k ′ \bm{k},\bm{k}' k , k ′
k ′ − k = G n = n 1 b 1 + n 2 b 2 + n 3 b 3 (37) \bm{k}' - \bm{k} = \bm{G}_n = n_1\bm{b}_1 + n_2\bm{b}_2 + n_3\bm{b}_3 \tag{37}
k ′ − k = G n = n 1 b 1 + n 2 b 2 + n 3 b 3 ( 3 7 )
当 E k = E k ′ E_{\bm{k}} = E_{\bm{k}'} E k = E k ′
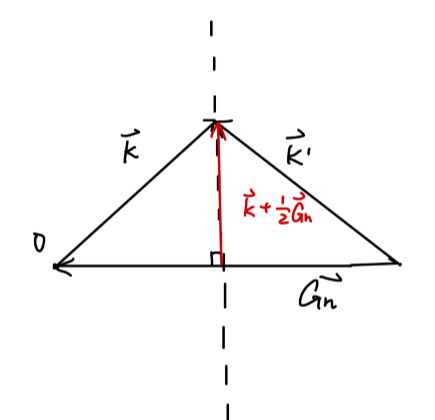
∣ k ∣ 2 = ∣ k + G n ∣ 2 ⇒ G n ⋅ ( k + 1 2 G n ) = 0 (38) \begin{aligned}
&|\bm{k}|^2 = |\bm{k}+\bm{G}_n|^2\\
& \Rightarrow \bm{G}_n \cdot (\bm{k} + \frac{1}{2}\bm{G}_n) = 0\\
\end{aligned}\tag{38}
∣ k ∣ 2 = ∣ k + G n ∣ 2 ⇒ G n ⋅ ( k + 2 1 G n ) = 0 ( 3 8 )
这就是考虑简并微扰计算的条件。具体可以用下图表示:
Fig:简并微扰计算的条件
我们发现,能够产生简并微扰的波矢正好落在倒点阵 WS元胞的边界上。WS元胞由一系列的倒格点连线的垂直平分面组成,如此这些平分面能够将整个空间分为一个个区域。在每个区域内,能量是连续变化的,在边界上能量会发生突变,我们称一个个这样的区域为 布里渊区 。
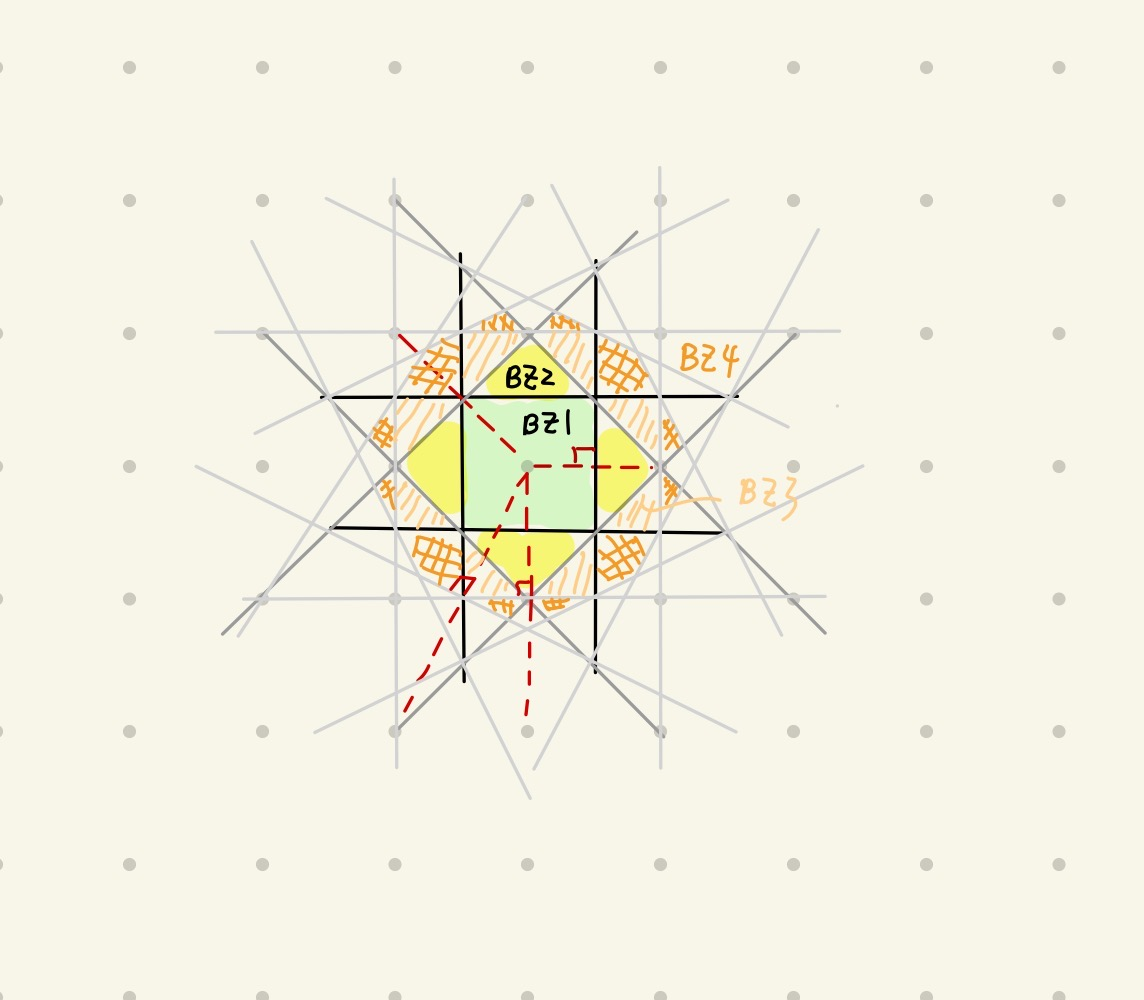
Fig:平面正方晶格的布里渊区
以平面正方晶格为例,其倒点阵也为平面正方点阵,如上图所示:
第一布里渊区 :所有近邻点的中垂面围成的区域。第二布里渊区 :所有次近邻点的中垂面与近邻点的中垂面围成的区域。第三布里渊区 :所有次次近邻点的中垂面与近邻点的中垂面围成的区域。第四布里渊区 :所有第三近邻点的中垂面与次次近邻、近邻点的中垂面围成的区域。
我们发现这些布里渊区是相互嵌套的:高级的布里渊区将低级的布里渊区包围住。且所有的布里渊区面积恒定,高极的布里渊区可以通过平移拼接成第一布里渊区。
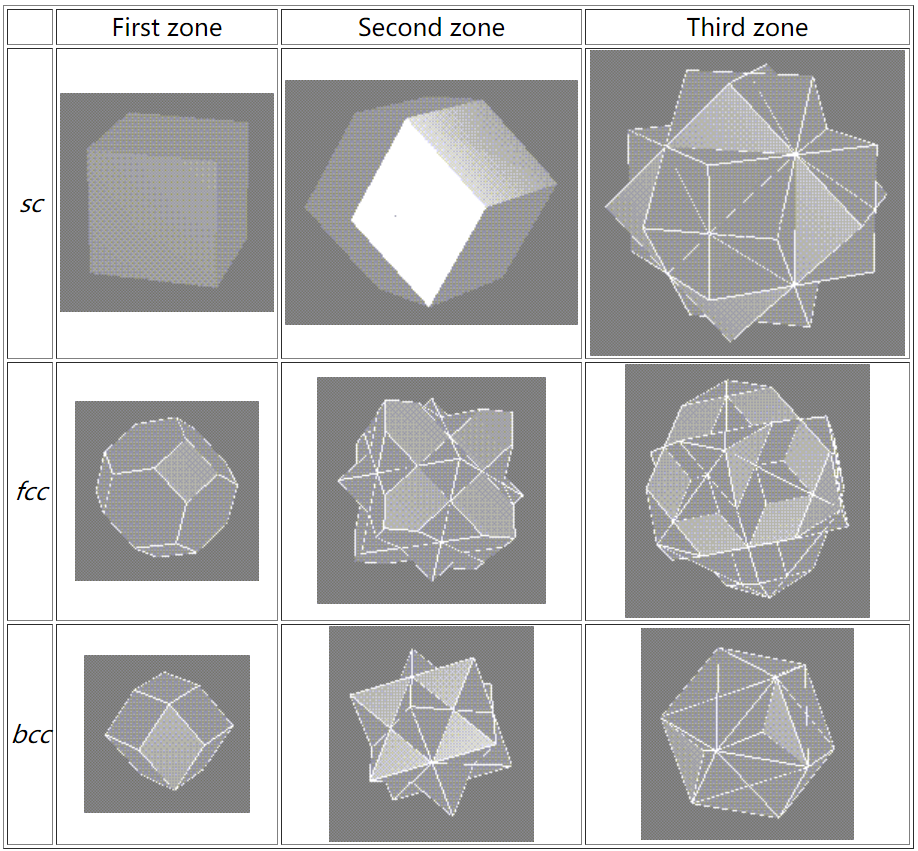
对于三维情况下的布里渊区,以下分别展示了简单晶格、面心立方晶格、体心立方晶格的布里渊区:
Fig:简单晶格、面心立方晶格、体心立方晶格的布里渊区[ 5 ] ^{[5]} [ 5 ]
在 Bloch 定理的表述中,能量是简约波矢 k \bm{k} k
E n ( k ) = E n ( k + K h ) (39) E^n(\bm{k}) = E^n(\bm{k}+\bm{K}_h)\tag{39}
E n ( k ) = E n ( k + K h ) ( 3 9 )
若布里渊区满足一定的对称性,这体现在使用点群对称操作 Q ^ \hat{Q} Q ^
Q ^ E ( k ) = E ( k ) (40) \hat{Q}E(\bm{k}) = E(\bm{k}) \tag{40}
Q ^ E ( k ) = E ( k ) ( 4 0 )
若具有时间反演对称性,则有:
E n ( k ) = E n ( − k ) (41) E^n(\bm{k}) = E^n(-\bm{k}) \tag{41}
E n ( k ) = E n ( − k ) ( 4 1 )
若 BZ 界面关于某一镜面对称,则有等能面垂直于该 BZ 界面。
这点利用对称性与周期性是容易得到的。
我们要注意区分简约波矢与自由电子波矢,简约波矢是平移算符本征值对应的量子数,周期场中单电子 H ^ \hat{H} H ^
ψ k n ( r ) = e i k ⋅ r u k n ( r ) \psi_{\bm{k}n}(\bm{r}) = e^{i\bm{k}\cdot\bm{r}}u_{\bm{k}n}(\bm{r})
ψ k n ( r ) = e i k ⋅ r u k n ( r )
我们可以将自由电子近似得到的能带结构,化为简约波矢表示,以满足 Bloch 定理的要求。
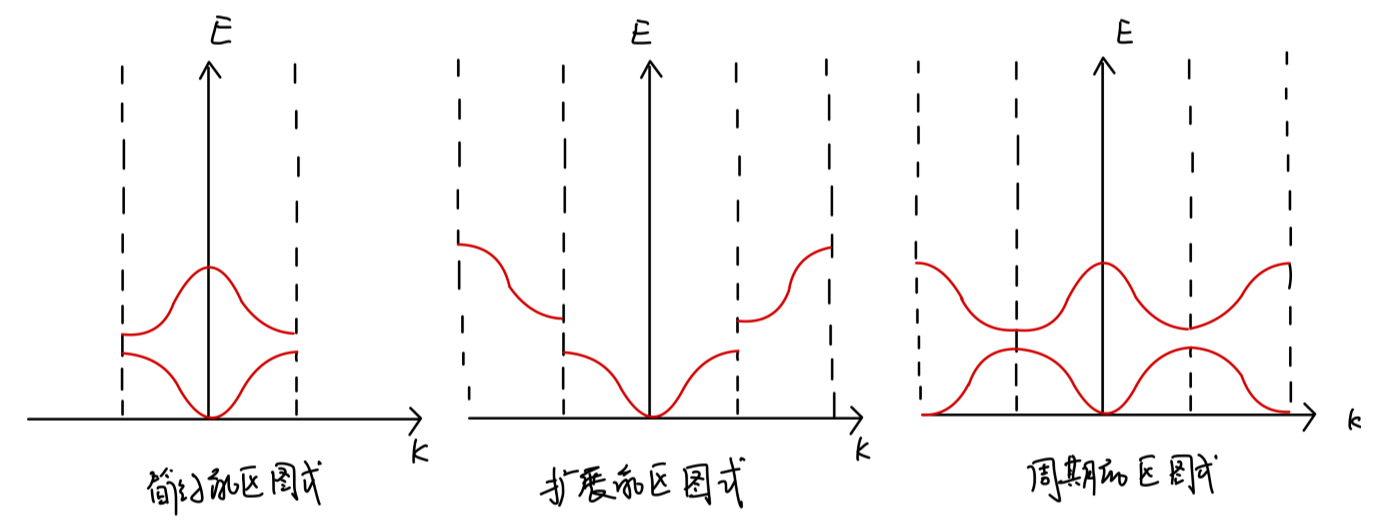
可以使用以下三种图示表示能带:简约能区图式,扩展能区图示,周期能区图示
Fig:能带的简约能区图式,扩展能区图示,周期能区图示
对于同一个简约波矢来说,其对应多个能带,为此我们引入量子数 n n n
维基百科编者. 德鲁德模型[G/OL]. 维基百科, 202120210508 . https://zh.wikipedia.org/w/index.php?title=德鲁德模型&oldid=65524723 .
由Rafaelgarcia - Electrona in crystallo fluentia.png. Uploader believes this faithful SVG reproduction constitutes a mere mechanical conversion between formats and as such cannot be considered a derivative work. Uploader accordingly believes uploader has no share in the copyright of this file.,CC BY-SA 3.0,https://commons.wikimedia.org/w/index.php?curid=11926841
胡安,章维益 固体物理学
黄昆,固体物理学
http://phycomp.technion.ac.il/~nika/brillouin_zones.html 封面图 By Inductiveload - Own work, Public Domain, https://commons.wikimedia.org/w/index.php?curid=3999372