固体物理笔记（二）：晶体的对称性

晶体的宏观对称性

晶体的宏观对称性与晶胞的对称性有关联。其宏观对称性不仅反映在规则的几何外观上，更体现在晶体的 宏观物理性质 上。

以介电常数为例：
各向同性材料的电磁性质方程为：

$\bm{D} = \varepsilon_0\varepsilon_r\bm{E}$

各向异性材料的电磁性质方程：

$D_\alpha = \sum_{\beta} \varepsilon_{\alpha\beta} E_{\beta}$

其中 $(\varepsilon_{\alpha\beta})$ 为介电张量。

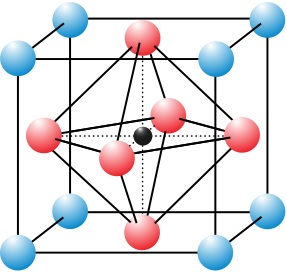
方解石 $^{[2]}$ 为六角结构：

由于对称性的限制，其介电张量将有以下形式（将会在后面仔细说明）：

$(\varepsilon_{\alpha\beta})=\begin{pmatrix} \varepsilon_{//} & 0 & 0\\ 0 & \varepsilon_{\perp} & 0\\ 0 & 0 & \varepsilon_{\perp} \\ \end{pmatrix}$

可得：

$\begin{aligned} &\bm{D}_{\perp} = \varepsilon_{\perp} \bm{E}_{\perp}\\ &\bm{D}_{//} = \varepsilon_{//} \bm{E}_{//}\\ \end{aligned}$

由此在垂直与平行两个方向上，方解石的折射率有差别。这就是双折射 $^{[3]}$ 产生的原因。

各向异性的物理性质与结构密切相关。

宏观对称性的描述

对称操作

如何描述对称性？要概括一个图形的对称性，就是考察在一定的几何变换之下物体的不变性。这种几何变换就是 对称操作。
例如对于以下图形，我们得到一些观察

旋转对称性：
- 圆：对绕中心的任何一个旋转都不变
- 正方形：对绕中心旋转 $90\degree$ 及其倍数不变
- 等腰梯形：对绕中心旋转任何角度都不保持不变
- 不规则图形：对绕中心旋转任何角度都不保持不变
反射对称性：
- 圆：对任意直径作反射都不变
- 正方形：只有对四条线作反射保持不变
- 等腰梯形：对上下中点连线作反射保持不变
- 不规则图形：没有

综合以上观察，对图形的对称性排序：
圆形 > 正方形 > 等腰梯形 > 不规则图形

旋转与反射这两类操作实质是一个坐标变换，可以用矩阵表示。并且这类变换具有一个特性：变换前后存在不动点。为了和平移对称性区分开来，我们称其为 点对称性。
点对称变换可以用变换矩阵 $A$ 表示：
对于一个任意点 $(x,y,z)$ 有：

$\begin{pmatrix} x \\ y \\ z \end{pmatrix} \longrightarrow \begin{pmatrix} x' \\ y' \\ z' \end{pmatrix} =(a_{ij})_{3\times3} \begin{pmatrix} x \\ y \\ z \end{pmatrix}$

记做：

$x' =Ax$

最基本的三种点对称变换为：

旋转

例如绕 $x$ 轴旋转 $\theta$ 。

$A = \begin{pmatrix} 1 & 0 & 0\\ 0 & \cos\theta & -\sin\theta\\ 0 & \sin\theta & \cos\theta\\ \end{pmatrix}$

反演

对原点进行反演。

$A = \begin{pmatrix} -1 & 0 & 0\\ 0 & -1 & 0\\ 0 & 0 & -1\\ \end{pmatrix}$

旋转反演

例如绕 $x$ 轴旋转 $\theta$ ，再对原点进行反演。

$A = \begin{pmatrix} -1 & 0 & 0\\ 0 & -\cos\theta & \sin\theta\\ 0 & -\sin\theta & -\cos\theta\\ \end{pmatrix}$

可以证明点对称变换是 正交变换： $A^TA = 1$ 。

证明：
变换前后，两点间距离保持不变（刚性条件）。不妨取 $(0,0,0)$ 为不动点。因此有 $(x,y,z)$ 与原点间的距离保持不变：

$x^2+y^2+z^2=x'^2+y'^2+z'^2$

写为矩阵形式：

$x^T x = x'^T x'$

由此可得：

$\begin{aligned} x'^Tx' &= (Ax)^T(Ax)\\ &= x^T A^TA x = x^T x \end{aligned}$

因此，刚性条件要求：

$A^TA = 1,\quad |A| = \pm1$

其中旋转操作 $|A|=1$ ，反演和旋转反演 $|A|=-1$ 。

如果一个物体在某正交变换下保持不变，就称这个变换是物体的一个 对称操作。一个物体所允许的对称操作数愈多，表明其对称性愈高。

对称素

指的是一个物体借以进行对称操作的一根轴、一个点或一个平面。

如果一个物体绕某轴旋转 $\frac{2\pi}{n}$ 及其倍数保持不变，则称这个轴为 $n$ 次（重）轴，记为 $n$ 。
如果一个物体对某点反演不变，称为这点为 反演中心，记为 $C_i$ 。
如果一个物体绕某轴旋转 $\frac{2\pi}{n}$ 后，再反演，最终不变。称为 $n$ 重（次）旋转反演轴（象转轴），记为 $\bar{n}$ 。

对于 $\bar{2}$ ，可以得到其等价于对一个平面的镜面操作 $m$ 。

例：立方体（ $O_h$ 群）

对称素	对称素个数	对称操作个数
$4$	3	9
$3$	4	8
$2$	1	6
$E$	1	1
$C_i$	1	1
$\bar{4}$	3	9
$\bar{3}$	4	8
$\bar{2}$	1	6

共有 48 个对称操作。

这点利用排列组合容易得到： $C_8^1A_3^3 = 48$

晶体的宏观对称性

群
在数学上，定义一组元素的集合为群：

$\mathcal{A} = \{E,A_1,A_2,\cdots,A_n\}$

赋予这些元素一定的乘法规则，使其满足：

若 $A_i,A_j \in \mathcal{A}$ ，则 $A_iA_j \in \mathcal{A}$ 。（群对乘法的封闭性）

存在单位元素，使得： $\forall A_i\in \mathcal{A},A_iE=EA_i =A_i$

存在逆元， $\forall A_i\in \mathcal{A},\ \exists A_i^{-1} \in \mathcal{A},\ s.t.\ A_iA_i^{-1}=A_i^{-1}A_i = E$

元素间的乘法满足结合律： $A_i(A_jA_k)=(A_iA_j)A_k$

一个物体的全部对称操作满足上述群的定义，称其构成一个 操作群。
例：立方体48个对称操作构成一个操作群，记为 $O_h$

现在讨论 晶体可能具有的宏观对称素。

微观对称性破缺，宏观对称性也必然破缺。

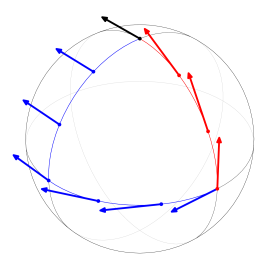
考虑对结点 $A,B$ 做如图旋转操作，得到 $A',B'$ 。容易得到： $AB//A'B'$ 。这两个晶列代表同一晶向，具有相同周期，有：

$\overline{B'A'} = n \overline{AB}$

根据几何关系：

$\overline{B'A'} = (1+2\cos\theta)\overline{AB}$

可得：

$\theta$	$n$	对称素
$0\degree$	$-1$	$1$
$60\degree$	$0$	$6$
$90\degree$	$1$	$4$
$120\degree$	$2$	$3$
$180\degree$	$3$	$2$

加上对应的反演 $C_i,\bar{2},\bar{3},\bar{4},\bar{6}$ ，总共有10种对称素。

现在讨论这10个对称素的独立性，不难发现：

$\bar{1} = C_i$
$\bar{2} = m$
$\bar{3} = 3+C_i$
$\bar{4}$ 是独立的。
$\bar{6}=3+m$

由此，独立的对称素为 $1,2,3,4,6,C_i,m,\bar{4}$ ，共有8个。

例如：正四面体

对称素	对称素个数	对称操作个数
$\bar{4}$	$3$	$6$
$3$	$4$	$8$
$m$	$6$	$6$
$2$	$3$	$3$
$E$	$1$	$1$

晶体周期性对于对称素组合的限制
可以证明：

两个二次轴之间的夹角只能是 $30\degree,45\degree,60\degree,90\degree$ 。

不可能多于两条六次轴，也不可能有一条六次轴和一条四次轴。

宏观对称性与宏观物性的关系

以电磁性质方程为例：

$D = \epsilon E$

在对称变换 $A$ 下：

$D' = AD,\quad E' =AE$

可得

$\begin{aligned} D' &= AD\\ & = A\epsilon E\\ & = (A\epsilon A^T)E'\\ & =\epsilon' E' \end{aligned}$

物体宏观性质应当在对称变换下保持不变，即：

$D' = \epsilon E'$

对比可得：

$\epsilon = A\epsilon A^T$

对于立方晶系，先选取 $x$ 轴为四重轴，旋转 $\theta = \frac{\pi}{2}$

$A = \begin{pmatrix} 1 & 0 & 0\\ 0 & \cos\theta & -\sin\theta\\ 0 & \sin\theta & \cos\theta\\ \end{pmatrix} = \begin{pmatrix} 1 & 0 & 0\\ 0 & 0 & -1\\ 0 & 1 & 0\\ \end{pmatrix}$

$\begin{aligned} A\epsilon A^{T} &= \begin{pmatrix} 1 & 0 & 0\\ 0 & 0 & -1\\ 0 & 1 & 0\\ \end{pmatrix}\begin{pmatrix} \epsilon_{11} & \epsilon_{12} & \epsilon_{13}\\ \epsilon_{21} & \epsilon_{22} & \epsilon_{23}\\ \epsilon_{31} & \epsilon_{32} & \epsilon_{33}\\ \end{pmatrix}\begin{pmatrix} 1 & 0 & 0\\ 0 & 0 & 1\\ 0 & -1 & 0\\ \end{pmatrix}\\ &=\begin{pmatrix} \epsilon_{11} & -\epsilon_{13} & \epsilon_{12}\\ -\epsilon_{31} & \epsilon_{33} & -\epsilon_{32}\\ \epsilon_{21} & -\epsilon_{23} & \epsilon_{22}\\ \end{pmatrix}\\ \end{aligned}$

可得：

$\left\{\begin{aligned} &\epsilon_{12} = -\epsilon_{13} \\ &\epsilon_{12} = \epsilon_{13} \\ \end{aligned}\right.$

应用其他对称操作，最终得到：

$\epsilon_{\alpha\beta} = \delta_{\alpha\beta}\epsilon_{0}$

即立方晶体介电常数为标量。

晶体对称性类型

对于宏观对称性，考虑到：

一种点阵的结构对应的点阵的宏观对称性显然高于本身的对称性
不同对称性的结构可以有相同的点阵

因此点阵的对称类型应该少于结构的对称类型。结构的点群为 晶体点群 ，共有 32 种；点阵的点群对应 7 个晶系；另外同时考虑到宏观对称性与平移对称性，晶系可分为 14 种 Bravais 格子（空间点阵）；晶体点群拓展为 230 种 空间群。

晶体点群

用 10 个对称素（8种）的基础上构成的对称性操作群叫做点群。可以证明，只有 32 种晶体点群。
可以使用 熊夫利符号 表示晶体点群 $^{[4]}$ ：

$C_n$ $C_{n}$ 循环群：有一跟根 $n$ $n$ 次旋转轴。
- $C_{nh}$ ： $C_n$ 加上一个与旋转轴垂直的镜面。
- $C_{nv}$ ： $C_n$ 加上一个与旋转轴平行的镜面。
$S_{2n}$ ： $n$ 为偶数：有一根 $2n$ 次象转轴； $n$ 为奇数：有一根 $n$ 次象转轴。
$D_n$ $D_{n}$ （二面体群）：有一根 $n$ $n$ 次轴和 $n$ $n$ 根垂直于这根主轴的二重轴。
- $D_{nh}$ ： $D_n$ 加上一个与旋转轴垂直的镜面。
- $D_{nd}$ ： $D_n$ 加上 $n$ 个与旋转轴平行的镜面。
$T$ $T$ （四面体群）：具有四面体对称性。
- $T_d$ ：包括旋转反映操作
- $T_h$ ：包括与旋转轴垂直的镜面。
$O$ $O$ （八面体群）：具有八面体或立方体的对称性
- $O_h$ ：包括旋转反映操作。

赫尔曼–莫甘记号 是晶体点群的国际标记符号，它用点群的特征对称素对点群进行标记。其遵循以下规则：

不同位置的数字表示不同方向的轴。
若 $n$ 次轴与 $m$ 垂直，记为 $\frac{n}{m}$ ，当不引起歧义时，可以简写为 $m$ 。
若多个轴方向相同，最后的符号要尽可能反映点群的对称性。
这几个对称素是独立的，能够通过相应的对称操作生成整个操作群。

32中点群对应的 熊夫利符号 与 赫尔曼–莫甘记号 列在下表：

序号	熊夫利符号	赫尔曼–莫甘记号（完整）	赫尔曼–莫甘记号（简写）	阶
1	$C_1$	$1$	$1$	$1$
2	$C_2$	$2$	$2$	$2$
3	$C_3$	$3$	$3$	$3$
4	$C_4$	$4$	$4$	$4$
5	$C_6$	$6$	$6$	$6$
6	$C_{1h} = C_{1v}$	$m$	$m$	$2$
7	$C_{2h}$	$\frac{2}{m}$	$2/m$	$4$
8	$C_{3h}$	$\bar{6}$	$\bar{6}$	$6$
9	$C_{4h}$	$\frac{4}{m}$	$4/m$	$8$
10	$C_{6h}$	$\frac{6}{m}$	$6/m$	$12$
11	$C_{2v}$	$mm2$	$mm2$	$4$
12	$C_{3v}$	$3m$	$3m$	$6$
13	$C_{4v}$	$4mm$	$4mm$	$8$
14	$C_{6v}$	$6mm$	$6mm$	$12$
15	$S_{2} = C_i$	$\bar{1}$	$\bar{1}$	$1$
16	$S_{4}$	$\bar{4}$	$\bar{4}$	$4$
17	$S_{6}$	$\bar{3}$	$\bar{3}$	$6$
18	$D_{2}$	$222$	$222$	$4$
19	$D_{3}$	$32$	$32$	$6$
20	$D_{4}$	$422$	$422$	$8$
21	$D_{6}$	$622$	$622$	$12$
22	$D_{2h}$	$\frac{2}{m}\frac{2}{m}\frac{2}{m}$	$mmm$	$8$
23	$D_{3h}$	$\bar{6}m2$	$\bar{6}m2$	$12$
24	$D_{4h}$	$\frac{4}{m}\frac{2}{m}\frac{2}{m}$	$4/mmm$	$16$
25	$D_{6h}$	$\frac{6}{m}\frac{2}{m}\frac{2}{m}$	$6/mmm$	$24$
26	$D_{2d}$	$\bar{4}2m$	$\bar{4}2m$	$8$
27	$D_{3d}$	$\bar{3}\frac{2}{m}$	$\bar{3}m$	$12$
28	$T$	$23$	$23$	$12$
29	$T_h$	$\frac{2}{m}\bar{3}$	$m\bar{3}$	$24$
30	$T_d$	$\bar{4}3m$	$\bar{4}3m$	$24$
31	$O$	$432$	$432$	$24$
32	$O_h$	$\frac{4}{m}\bar{3}\frac{2}{m}$	$m\bar{3}m$	$48$

各个对称素的生成关系可以用下图表示：

晶系与 Bravais 格子

只考虑格点的宏观对称性可以将 32种晶体点群划分为 7 种晶系（根据特征对称素的不同）。
考虑点阵的平移对称性，可以将晶系分为：简单（P），体心（B），面心（F），底心（I）。

晶系、Bravais 格子的相关信息列在下表。

晶系	单胞基矢的特性	特征对称素	Bravais 格子	所属点群
三斜晶系	$a_1\neq a_2\neq a_3$ ，夹角不等	无	简单三斜（P）	$C_1,C_i$
单斜晶系	$a_1\neq a_2\neq a_3$ , $a_2\perp a_1,a_3$	一个2次轴或对称面	简单单斜（P），底心单斜（I）	$C_2,C_s,C_{2h}$
正交晶系	$a_1\neq a_2\neq a_3$ , $a_1,a_2,a_3$ 相互正交	3个相互垂直的2次轴或2个互相垂直对称面	简单正交（P），底心正交（I），体心正交（B），面心正交（F）	$D_2,C_{2v},D_{2h}$
三方晶系	$a_1=a_2=a_3$ , $\alpha=\beta=\gamma<120\degree,\neq 90\degree$	在一个方向上有3次轴	简单三方（P）	$C_3,C_{3i},D,C_{3v},D_{3d}$
四方晶系	$a_1=a_2\neq a_3,\alpha=\beta=\gamma=90\degree$	在一个方向上有4次轴	简单四方（P），体心四方（B）	$C_4,C_{4h},C_{4v},D_{4},D_{4h},D_{2d},S_4$
六方晶系	$a_1=a_2\neq a_3,\ \ a_3\perp a_1,a_2,\ \ \angle a_1a_2 = 120\degree$	在一个方向上有6次轴	简单六角（P）	$C_6,C_{6h},C_{3v},D_{6},D_{6h},C_{3h},D_{2h}$
立方晶系	$a_1=a_2\neq a_3，\alpha=\beta=\gamma=90^\degree$	4个按照立方对角线排列的方向上有3次轴	简单立方（P），体心立方（B），面心立方（F）	$T,T_h,T_d,O,O_h$