角动量
角动量与对称性
我们现在假设空间是 各向同性 的:所有的空间方向都是一样的,当整个系统绕任意轴转过任意角之后,该封闭系统的哈密顿量不会改变。在经典力学中,空间各向同性对应着角动量守恒。现在我们考虑对波函数的无限小操作所给出的结果:
这实际上体现了李群与李代数的关系。空间旋转群是一个李群,我们通过无穷小变换得到角动量的代数结构,反之角动量可以通过指数映射得到旋转群。在量子场论中,我们会进行更加细致的说明。
考虑一个无限小旋转操作 δφ,其模为转角 δφ,方向为转轴方向。粒子的位矢在此旋转操作下的位移为:
δrα=δφ×rα(1)
任意波函数在经过无穷小旋转后变换得到下列函数:
ψ(r1+δr1,r2+δr2,⋯)=ψ(r1,r2,⋯)+α∑δrα⋅∇αψ=ψ(r1,r2,⋯)+α∑δφ×rα⋅∇αψ=(1+δφ⋅α∑rα×∇α)ψ(r1,r2,⋯)(2)
其中:
1+δφ⋅α∑rα×∇α
可以看作无限小旋转算子。由无限小旋转算子不改变哈密顿量。由此:无限小旋转算子应当与哈密顿算子对易。考虑到 δφ 选取的任意性,可以得到:
[α∑rα×∇α,H^]=0(3)
这对应着某种守恒量。而空间的各向同性告诉我们,这个守恒量不是别的,正是角动量。因此 ∑αrα×∇α 应当与角动量算子至多相差一个系数。
考虑坐标表象下的一次量子化程式:
p^→iℏ∇
由此,容易类比得到 角动量算子 在坐标表象中的表达式:
⇒L=r×pL^=r^×p^=iℏr×∇(4)
其分量式为:
L^xL^yL^z=iℏ(yp^z−zp^y)=iℏ(zp^x−xp^z)=iℏ(xp^y−yp^x)(5)
这三个算子对应三个角动量分量,都是厄密算子。
在球坐标下,角动量算子可以表示为:
L^=iℏr^×∇=iℏrer×(er∂r∂+eθr1∂θ∂+eϕrsinθ1∂ϕ∂)=iℏ(−eθsinθ1∂ϕ∂+eϕ∂θ∂)(6)
再回到直角坐标,得到三个分量算子可以使用角坐标表示为:
L^x=L^y=L^z=iℏ(−sinϕ∂θ∂−cotθcosϕ∂ϕ∂)iℏ(cosϕ∂θ∂−cotθsinϕ∂ϕ∂)iℏ∂ϕ∂(7)
角动量平方对应的算子 L^2 也经常用到,有:
L^2=L^x2+L^y2+L^z2=−ℏ2(sinθ1∂θ∂(sinθ∂θ∂)+sin2θ1∂φ2∂2)(8)
角动量算子的基本性质
在得到角动量算子的表达式后,我们可以讨论其的一些性质。
对易关系
[L^x,x^][L^x,y^][L^x,z^]=[y^p^z−z^p^y,x^]=0=[y^p^z−z^p^y,y^]=−z^[p^y,y^]=iℏz^=[y^p^z−z^p^y,z^]=y^[p^z,z^]=−iℏy^
一般的情况下有:
[L^α,x^β]=[εαμνx^μp^ν,x^β]=εαμνx^μ[p^ν,x^β]=−εαμνx^μiℏδνβ=−εαμβx^μiℏ=εαβγx^γiℏ
上式中已经默认使用爱因斯坦求和法则。最后一步更换了哑标。下直接推导一般关系。
[L^α,p^β]=[εαμνx^μp^ν,p^β]=εαμν[x^μ,p^β]p^ν=εαμνp^νiℏδμβ=εαβνp^νiℏ=εαβγp^γiℏ
[L^α,L^β]=[L^α,εβμνx^μp^ν]=εβμν([L^α,x^μ]p^ν+x^μ[L^α,p^ν])=iℏεβμν(εαμλx^λp^ν+εανλx^μp^λ)=iℏ(εβμνεαμλ+εβλμεαμν)x^λp^ν=iℏ(δαβδνλ−δανδβλ+δαλδβν−δαβδνλ)x^λp^ν=iℏ(δαλδβν−δανδβλ)x^λp^ν=iℏ(x^αp^β−x^βp^α)=iℏεαβγL^γ
这表明三个角动量分量是不能够同时确定的。
注意上式第三步对第二项更换哑标:
μ→λλ→νν→μ
使得两项可以合并。
我们发现,上述三个对易关系的结果是类似的,即:
[L^α,x^β]=iℏεαβγx^γ[L^α,p^β]=iℏεαβγp^γ[L^α,L^β]=iℏεαβγL^γ(9)
现在考虑角动量平方的算子 L^2 的对易关系。
[L^2,L^β]=[L^α2,L^β]=L^α[L^α,L^β]+[L^α,L^β]L^α=iℏεαβγ(L^αL^γ+L^γL^α)=iℏεαβγ{L^α,L^γ}
上式中最后有一反对易式:
{A^,B^}=A^B^+B^A^
于是反对易式 {L^α,L^γ} 关于指标 α,γ 是对称的。而 εαβγ 关于指标 α,γ 是反对称的。于是可得:
[L^2,L^β]=0(10)
即角动量平方算子与三个角动量分量算子对易。于是角动量平方可以与其中一个分量同时确定。这点十分重要。
在球坐标中,L^z 的形式是简单的。而 L^x,L^y 的形式较为复杂。一般情况下,我们常常使用以下组合的算子:
L^+=L^x+iL^yL^−=L^x−iL^y(11)
L^± 不是厄密算子,有:
L^±†=L^∓
使用球坐标表出的形式为:
L^+=ℏeiϕ(∂θ∂+icotθ∂θ∂)L^−=ℏe−iϕ(−∂θ∂+icotθ∂θ∂)(12)
计算对易关系:
[L^+,L^−]=[L^x+iL^y,L^x−iL^y]=i[L^y,L^x]−i[L^x,L^y]=−2i[L^x,L^y]=2ℏL^z(13)
[L^±,L^z]=[L^x±iL^y,L^z]=iℏ(−L^y±iL^x)=∓ℏL^±(14)
容易得到:
[L^2,L^±]=0(15)
另外 L^± 与 L^2,L^z 具有如下关系:
L^+L^−=(L^x+iL^y)(L^x−iL^y)=L^x2+L^y2−i[L^x,L^y]=L^2−L^z2+ℏL^z(16)
本征值与本征函数
为了求体系在某一方向的角动量,不妨选取该方向为极轴,在球坐标下求解以下本征值方程:
L^zψ(r,θ,ϕ)=Lzψ(r,θ,ϕ)(17)
其中 L^z=iℏ∂ϕ∂。方程 (17) 的解为:
ψ(r,θ,ϕ)=f(r,θ)eimϕ(18)
考虑到周期性边界条件:
ψ(r,θ,ϕ)=ψ(r,θ,ϕ+2π)⇒ei2πm=1
于是得到 m∈Z。
于是 L^z 的本征值为:
Lz=mℏ,m=0,±1,±2,⋯(19)
这个结论也适用于 L^x,L^y。任意方向上的角动量只能取整数值,这点看起来十分奇怪,但要注意,除了 Lx=Ly=Lz=0 的情况。这三个角动量算子并没有共同本征态,即三个角动量不能同时确定。一旦给定了一个分量的角动量,另外方向的角动量都是不确定的值 [1]。
角动量平方算子与角动量算子是对易的,角动量的模方与其中一个角动量分量是可以同时确定的。我们来考虑角动量平方算子的本征值方程:
L^2ψ(r,θ,φ)=L2ψ(r,θ,φ)(20)
在球坐标下写为:
−ℏ2(sinθ1∂θ∂(sinθ∂θ∂)+sin2θ1∂φ2∂2)ψ(r,θ,φ)=L2ψ(r,θ,φ)
即:
sinθ1∂θ∂(sinθ∂θ∂ψ)+sin2θ1∂φ2∂2ψ+ℏ2L2ψ=0(21)
这就是 球函数方程,在数学物理方法中我们已经得到此类方程的本征函数为 球谐函数 Ylm(θ,φ)。本征值为:
L2=l(l+1)ℏ2,l=0,1,2,⋯(22)
综合来说,{L^2,L^z} 的共同本征态就是球谐函数 Ylm,l=0,1,2,⋯,m=0,±1,⋯,±l,对应的本征值为:
L2=l(l+1)ℏ2,Lz=mℏ(23)
在本征态 Ylm 上,可以如下平均值:
Lx=LyLx2=Ly2=0=21(L2−Lz2)=21(l(l+1)−m2)ℏ2(24)
考虑对易关系 (14),来看看 L^± 作用于 Ylm 上的结果:
L^zL^±Ylm=([L^z,L^±]+L^±L^z)Ylm=(m±1)ℏL^±Ylm
于是 L^±Ylm 成为 L^z 本征值为 (m±1)ℏ 的本征态,那么有:
L^±Ylm=λYl,m±1
现在求归一化系数 λ。
⟨L^±Ylm∣L^±Ylm⟩=⟨Ylm∣L^±†L^±∣Ylm⟩=⟨Ylm∣L^∓L^±∣Ylm⟩=⟨Ylm∣L^2−L^z2∓ℏL^z∣Ylm⟩=(l(l+1)−m(m±1))ℏ2=λ2ℏ2(25)
可以得到:
L^+Ylm=l(l+1)−m(m+1)ℏYl,m+1L^−Ylm=l(l+1)−m(m−1)ℏYl,m−1(26)
对于 m=±l 时,有:
L^+Yl,l=0L^−Yl,−l=0(27)
这点是容易理解的。借助 L^+,L^−,我们联系起了相同角量子数、不同磁量子数的本征态。
角动量表象
{L^2,L^z} 的本征函数为球谐函数 Ylm,其本征态 ∣lm⟩ 可以用角量子数 l 与磁量子数 m 标志。另外,{∣lm⟩} 可以成为一组完备基底,用这组基底来表示算子、态矢就称为在 角动量表象 中的表示。
容易得到以下算子在角动量表象中的矩阵元:
⟨l′m′∣L^2∣lm⟩=l(l+1)ℏ2δl′lδm′m⟨l′m′∣L^z∣lm⟩=mℏδl′lδm′m⟨l′m′∣L^+∣lm⟩=l(l+1)−m(m+1)ℏδl′lδm′,m+1⟨l′m′∣L^−∣lm⟩=l(l+1)−m(m−1)ℏδl′lδm′,m−1(28)
结合 (28) 后两式,得到:
⟨l′m′∣L^x∣lm⟩=2ℏδl′l(l(l+1)−m(m+1)δm′,m+1+l(l+1)−m(m−1)δm′,m−1)⟨l′m′∣L^y∣lm⟩=2iℏδl′l(l(l+1)−m(m+1)δm′,m+1−l(l+1)−m(m−1)δm′,m−1)
可以得到这些算子都将是块对角的形式(每一个块对应一个角量子数)。
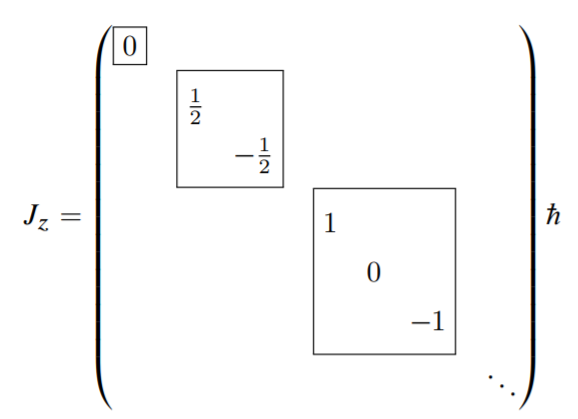
Fig:角动量的矩阵表示[3]
参考资料
- 朗道 量子力学
- Sakurai - Modern Quantum Mechanics
- http://staff.ustc.edu.cn/~shmj/Handout/Chapter8.pdf
- 封面图 By Maschen - Own work, Public Domain, https://commons.wikimedia.org/w/index.php?curid=17763200