量子力学笔记（七）：电磁作用

有电磁场时的薛定谔方程

最小电磁耦合原理

在建立薛定谔方程的一次量子化程式中，我们使用了：

$\left\{ \begin{aligned} & E\rightarrow i\hbar \frac{\partial}{\partial t}\\ & \bm{p} \rightarrow -i\hbar \nabla \\ \end{aligned} \right.\tag{1}$

在存在电磁场的情况下，按经典规则，$H-q\varphi$ 和 $\bm{p} - \frac{q}{c}\bm{A}$ 将对应无场时的 $H$ 和 $\bm{p}$。

这就是说，在考虑电磁场后的哈密顿量为：

$H = \frac{1}{2m}(\bm{p} - \frac{q}{c}\bm{A})^2 + q\varphi$

哈密顿正则方程给出：

$\left\{ \begin{aligned} & \bm{v} = \frac{\partial H}{\partial \bm{p}} = \frac{1}{m}(\bm{p} - \frac{q}{c}\bm{A})\\ & \dot{\bm{p}} = -\frac{\partial H}{\partial \bm{x}} = -q\nabla\varphi + \frac{q}{c}\sum_{i}v_i\frac{\partial A_i}{\partial \bm{x}} \\ \end{aligned} \right.$

考虑到：

$\dot{\bm{A}} = \frac{\partial \bm{A}}{\partial t} + (\bm{v}\cdot\nabla)\bm{A}$

且电场强度 $\bm{E}$、磁感应强度 $\bm{B}$ 与电势、磁矢势具有如下关系：

$\bm{E} = -\frac{1}{c}\frac{\partial \bm{A}}{\partial t} - \nabla \varphi,\quad \bm{B} = \nabla\times\bm{A}$

可以得到：

$m\dot{\bm{v}} = q\bm{E} + \frac{q}{c}[\sum_{i}v_i\frac{\partial A_i}{\partial \bm{x}} - (\bm{v}\cdot\nabla)\bm{A}]$

其中可以得到：

$\begin{aligned} \sum_{i}v_i\frac{\partial A_i}{\partial \bm{x}} - (\bm{v}\cdot\nabla)\bm{A} &= \nabla_{v}(\bm{v}\cdot\bm{A}) - (\bm{v}\cdot\nabla)\bm{A}\\ &= \bm{v}\times(\nabla\times\bm{A})\\ &= \bm{v}\times\bm{B}\\ \end{aligned}$

如此，得到带电粒子的动力学方程为：

$m\dot{\bm{v}} = q(\bm{E} + \frac{1}{c}\bm{v}\times\bm{B})$

这与我们的预期是一致的：带电粒子在电磁场中受到电场力与洛伦兹力的作用。

如此为了引入电磁场，只需要将一次量子化程式修改为：

$\left\{ \begin{aligned} & E\rightarrow i\hbar \frac{\partial}{\partial t} - q\varphi\\ & \bm{p} \rightarrow -i\hbar \nabla - \frac{q}{c}\bm{A} \\ \end{aligned} \right.\tag{2}$

这种将电磁场引入薛定谔方程的方法称为 最小电磁耦合原理。实际上，这是一个假设，但现在所发现的电磁相互作用均满足这一原理。之后我们将看到，电磁场与薛定谔方程在位相变化下的不变性相关。

得到有电磁场存在时的薛定谔方程为：

$i\hbar \frac{\partial \psi}{\partial t} = [\frac{1}{2m}(-i\hbar \nabla - \frac{q}{c}\bm{A})^2 + V + q\varphi]\psi \tag{3}$

注意区分机械动量 $(-i\hbar \nabla - \frac{q}{c}\bm{A})$ 与正则动量 $(-i\hbar\nabla)$。在无电磁场时，两者是相等的。

粒子的速度算子对应于机械动量：

$\hat{\bm{v}} = -\frac{1}{m}(i\hbar\nabla + \frac{q}{c}\bm{A})\tag{4}$

引入电磁场后，概率流成为：

$\begin{aligned} \bm{j} &= \mathrm{Re}(\psi^* \hat{\bm{v}} \psi)\\ &= \mathrm{Re}(\psi^*(-\frac{1}{m}(i\hbar\nabla + \frac{q}{c}\bm{A}))\psi) \end{aligned}\tag{5}$

我们现在从波函数的位相变换来考虑。薛定谔方程为：

$(-\frac{\hbar^2}{2m}\nabla^2+V)\psi = i\hbar\frac{\partial \psi}{\partial t}\tag{6}$

考虑一位相变换：

$\psi \rightarrow \psi' = \psi e^{i\lambda(\bm{r},t)}\tag{7}$

变换前后有：$\rho = \psi^*\psi = \psi'^*\psi' = \rho'$。对应的概率密度相同。波函数的相位应当是一个“额外的自由度”，它不会影响薛定谔方程所给出的解。这意味着，薛定谔方程的形式应当在位相变换下保持不变：

$(-\frac{\hbar^2}{2m}\nabla^2+V)\psi' = i\hbar\frac{\partial \psi'}{\partial t}\tag{8}$

将 $(7)$ 代入 $(8)$ 得到：

$[(-\frac{\hbar^2}{2m}\nabla^2+V)\psi] e^{i\lambda(\bm{r},t)} + \frac{\hbar^2}{2m}\psi e^{i\lambda(\bm{r},t)} \nabla^2 \lambda(\bm{r},t)= i\hbar\frac{\partial \psi}{\partial t}e^{i\lambda(\bm{r},t)} - \hbar\psi e^{i\lambda(\bm{r},t)} \frac{\partial \lambda(\bm{r},t)}{\partial t}$

考虑 $(6)$，得到：

$\frac{\hbar^2}{2m}\nabla^2 \lambda(\bm{r},t) = -\hbar \frac{\partial \lambda(\bm{r},t)}{\partial t} \tag{9}$

若对于特定的变换，$(9)$ 式成立，那么对应有薛定谔方程的形式在波函数的位相变换下不变。例如 $\lambda = \mathrm{const}$。然而，并不是对于所有的 $\lambda(\bm{r},t)$，薛定谔方程都具有这样的性质，这与我们之前的讨论是不符合的。

现在我们继续说明：在引入电磁场后，这个问题将得到解决：波函数的位相变换唯一确定了电磁场的规范变换。在经典物理学中我们得到：电磁场在规范变换下是不变的。对应的薛定谔方程也不会发生变化。从另一个角度来看，正是薛定谔方程对波函数位相变换的不变性要求引入电磁场。

$\psi'$ 满足的方程为：

$i\hbar \frac{\partial \psi'}{\partial t} = [\frac{1}{2m}(-i\hbar \nabla - \frac{q}{c}\bm{A}')^2 + V + q\varphi']\psi' \tag{10}$

将 $(7)$ 代入以上方程，分别考虑：

$\begin{aligned} &(i\hbar\frac{\partial \psi'}{\partial t}-(V+q\varphi')\psi') = e^{i\lambda}(i\hbar \frac{\partial \psi}{\partial t} - (V+q\varphi)\psi) + \psi'(-\hbar \frac{\partial \lambda}{\partial t} + q(\varphi-\varphi'))\\ &(-i\hbar\nabla-\frac{q}{c}\bm{A}')\psi' = e^{i\lambda}(-i\hbar\nabla-\frac{q}{c}\bm{A})\psi + \psi' (\hbar\nabla\lambda + \frac{q}{c}(\bm{A}-\bm{A}')) \end{aligned}$

在上式中，我们发现只要对电磁场做如下变换：

$\left\{ \begin{aligned} \varphi' &= \varphi - \frac{\hbar}{q}\frac{\partial \lambda}{\partial t}\\ \bm{A}' &= \bm{A} + \frac{\hbar c}{q}\nabla \lambda \end{aligned} \right.$

令 $\lambda(\bm{r},t) = \frac{q}{\hbar c} f(\bm{r},t)$，得到：

$\left\{ \begin{aligned} \varphi' &= \varphi - \frac{1}{c}\frac{\partial f}{\partial t}\\ \bm{A}' &= \bm{A} + \nabla f \end{aligned} \right.\tag{11}$

这不是别的，正是电磁场的 规范变换。电磁场的规范变换自由度对应薛定谔方程的位相变换自由度。

对称性是物理学中很深刻、美妙的思想。在规范场论中，位相变换对应 $U(1)$ 规范群，该群给出了电磁相互作用。规范原理因而可以视作以一种自然的方式引入了电子场与电磁场间的最小耦合$^{[2]}$。

粒子在电磁场中的运动

均匀磁场下粒子的运动—无自旋情况

均匀磁场下粒子在中心场的运动

对应处于均匀磁场中的单电子氢原子问题。

此时可以取对称规范：

$V(r) = -\frac{e^2}{r},\quad \bm{A} = \frac{1}{2}\bm{B} \times \bm{r}\tag{12}$

哈密顿量为：

$\begin{aligned} H &= \frac{1}{2m}(\bm{p}+\frac{e}{c}\bm{A})^2 - \frac{e^2}{r}\\ &= \frac{1}{2m}(p^2 + 2\frac{e}{c}\bm{A}\cdot\bm{p} + \frac{e\hbar}{ic}(\nabla\cdot\bm{A}) + \frac{e^2}{c^2}A^2)- \frac{e^2}{r}\\ & = \frac{p^2}{2m}-\frac{e^2}{r} + \frac{e\bm{B}}{2mc}\cdot\bm{L} + \frac{e^2}{8mc^2}(B^2r^2-(\bm{B}\cdot\bm{r})^2) \end{aligned}\tag{13}$

考虑 $\bm{B}$ 沿 $z$ 轴的情况。此时取：

$B = (0,0,B),\quad A = (-\frac{y}{2},\frac{x}{2},0)B\tag{14}$

代入 $(13)$ 得到：

$H = H_0 + \frac{eBL_z}{2mc} + \frac{e^2B^2}{8mc^2}(x^2+y^2) \tag{15}$

$H_0$ 代表不加磁场时的哈密顿量。对于 $(15)$ 给出的哈密顿量。我们考虑第二项与第三项的比值：

$\frac{eBL_z}{2mc}/\frac{e^2B^2}{8mc^2}(x^2+y^2) = \frac{eB}{4c} \frac{x^2+y^2}{L_z} \sim \frac{eBa^2}{c\hbar}$

$a$ 为波尔半径：

$a = \frac{\hbar^2}{m e^2}$

$\begin{aligned} &|E_1| = \frac{e^2}{2a} = -13.6\mathrm{eV}\\ &\mu_B = \frac{e\hbar}{2\mu c} \approx 5.8 \times 10^{-5}\mathrm{eV/T} \end{aligned}$

得到：

$\frac{eBa^2}{c\hbar} = \frac{\mu_BB}{|E_1|} \sim 10^{-6}\mathrm{B}/T \ll 1$

因此 $(15)$ 式中第三项在通常情况下是很小的。第二项可以写为：

$H_1 = \frac{eB}{2\mu c}L_z = -\bm{M}\cdot\bm{B}$

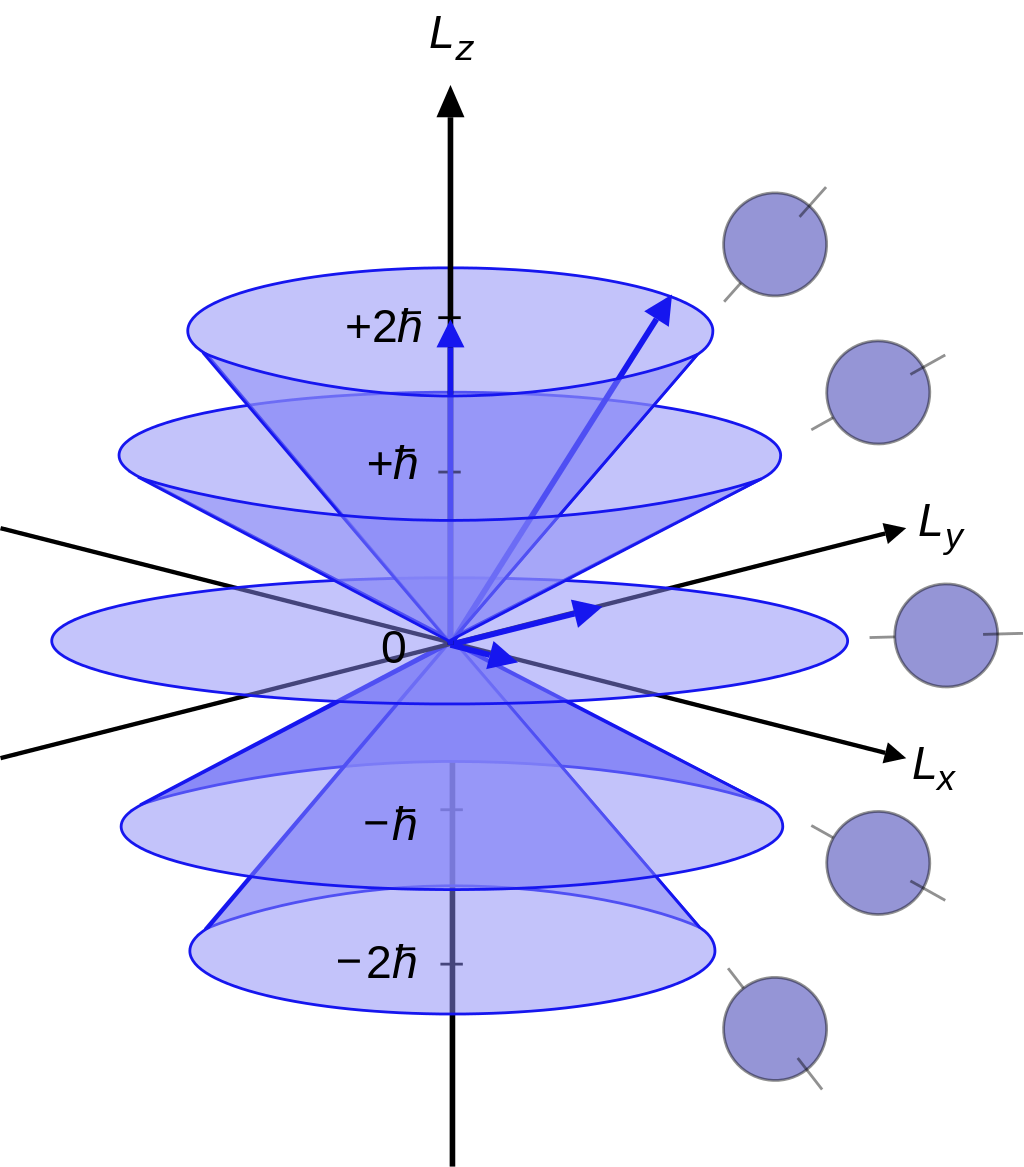
此时，$(\hat{H},\hat{L}^2,\hat{L}_z)$ 仍然具有共同本征态。哈密顿算子作用于本征波函数，可以得到：

$\begin{aligned} E &= E_{nlm}\\ &= E_{nl}^{(0)} + m\frac{e\hbar}{2\mu c}B\\ &= E_{nl}^{(0)} + m\mu_BB\\ &= E_{nl}^{(0)} + m\hbar\omega_L \end{aligned}\tag{16}$

$\omega_L = \frac{e\hbar}{2\mu c}$ 称为 拉莫频率。

加上外磁场后，系统的球对称性遭到破坏，原有的能级关于磁量子数 $m$ 的简并解除了。这种效应称为 正常塞曼效应。

均匀磁场下自由带电粒子运动

自由电子在均匀磁场中的哈密顿量为：

$H = \frac{1}{2m}(\bm{p}+\frac{e}{c}\bm{A})^2$

考虑磁场沿着 $z$ 轴。采用 朗道规范，即：

$\bm{A} = (0,x,0)B,\quad \bm{B} = (0,0,B)$

可以将哈密顿量写为：

$H = \frac{1}{2m}[p_x^2 + (p_y+\frac{e}{c}xB)^2 + p_z^2]\tag{17}$

那么对应的薛定谔方程为：

$\frac{1}{2m}[\hat{p}_x^2 + (\hat{p}_y+\frac{e}{c}xB)^2 + \hat{p}_z^2]\psi(x,y,z) = E\psi(x,y,z) \tag{18}$

注意到如下对易关系：

$[\hat{H},\hat{p}_y]=[\hat{H},\hat{p}_z] = 0$

如此，可以取本征波函数为如下形式：

$\psi(x,y,z) = \psi(x)\exp(i\frac{p_y y}{\hbar})\exp(i\frac{p_z z}{\hbar}) \tag{19}$

代入 $(18)$ 得到：

$\frac{1}{2m}[\hat{p}_x^2 + (p_y+\frac{e}{c}xB)^2 + p_z^2]\psi(x) = E\psi(x) \tag{20}$

写为如下形式：

$[\frac{e^2B^2}{2mc^2}(x + \frac{p_yc}{eB})^2 + \frac{1}{2m}\hat{p}_x^2]\psi(x) = (E-\frac{p_z^2}{2m})\psi(x) \tag{21}$

观察得到，左边实际上是一个谐振子的哈密顿量。有：

$\omega = \frac{eB}{mc}$

得到在均匀磁场中自由电子的能级为：

$E_{np_z} = (n+\frac{1}{2})\hbar\omega + \frac{p_z^2}{2m} \tag{22}$

这称为 朗道能级。

均匀磁场下束缚粒子的运动（考虑自旋）

求解中心场加均匀磁场下 $\frac{1}{2}$ 的自旋粒子的薛定谔方程。

考虑了自旋磁矩、轨道磁矩在外场中能量以及轨道-自旋耦合能量，哈密顿量为：

$H = \frac{p^2}{2m} - \frac{e^2}{r} + \xi(r)\bm{L}\cdot\bm{S} + \frac{eB}{2mc}(L_z + 2S_z)\tag{23}$

此处已经假定了外磁场沿着 $z$ 轴：

$\xi(r) = \frac{e^2}{2m^2c^2} - \frac{1}{r^3}$

现在我们只在给定量子数 $n,l$ 的子空间内进行研究，如此得到：

$\xi_{nl} = \langle nl|\xi(r)|nl\rangle$

可以使用 $\xi_{nl}$ 替代 $\xi(r)$ 写入方程。令：

$\alpha = \hbar^2 \xi_{nl},\quad \beta = \frac{eB\hbar}{2mc},\quad H_0 = \frac{p^2}{2m} - \frac{e^2}{r}$

代入 $(23)$，得到：

$H = H_0 + \alpha \bm{L}\cdot \bm{S} + \beta (L_z + 2S_z)$

注意：此处我们已经将 $\bm{L},\bm{S}$ 换成了无量纲的量。而 $\alpha,\beta$ 都具有能量的量纲。

考虑到：

$\bm{L}\cdot\bm{S} = \frac{1}{2}(L_z\sigma_z + L_+\sigma_- + L_-\sigma_+)$

此处：$L_{\pm} = L_x \pm i L_y,\quad \sigma_{\pm} =\frac{1}{2}(\sigma_{x} + i\sigma_{y})$

于是哈密顿量可以写为：

$H = H_0 + \beta L_z + (\beta + \frac{\alpha}{2}L_z)\sigma_z + \frac{\alpha}{2}(L_+\sigma_- + L_-\sigma_+)\tag{24}$

此时 $(H,L^2,S^2,L_z)$ 具有共同本征态 $|nlm_j\rangle$

代入本征值方程中得到：

$(H_0 + \beta L_z + (\beta + \frac{\alpha}{2}L_z)\sigma_z + \frac{\alpha}{2}(L_+\sigma_- + L_-\sigma_+))|nlm_j\rangle = E|nlm_j\rangle$

写为矩阵形式，有：

$\begin{pmatrix} H_0 + \beta L_z + (\beta + \frac{\alpha}{2}L_z) & \frac{\alpha}{2}L_{-}\\ \frac{\alpha}{2}L_{+} & H_0 + \beta L_z - (\beta + \frac{\alpha}{2}L_z)\\ \end{pmatrix}|nlm_j\rangle = E|nlm_j\rangle\tag{25}$

取 $m_j$ 为固定值，能满足上述本征值方程的解具有如下形式：

$|nlm_j\rangle = \begin{pmatrix} r_1|nlm\rangle \\ r_2|nl,m+1\rangle \\ \end{pmatrix}\tag{26}$

将 $(26)$ 代入 $(25)$ 得到如下方程组：

$\left\{ \begin{aligned} & r_1(H_0 + \beta m + (\beta + \frac{\alpha}{2}m)) + r_2\frac{\alpha}{2}\sqrt{l(l+1)-m(m+1)} = 0\\ & r_1\frac{\alpha}{2}\sqrt{l(l+1)-m(m+1)} + r_2(H_0 + \beta m - (\beta + \frac{\alpha}{2}m)) = 0\\ \end{aligned} \right.$

令该方程组的行列式为零，可以得到本征能量为：

$E^{(\pm)} = E_{nl} + (m+\frac{1}{2})\beta - \frac{\alpha}{4} \pm \frac{1}{2}\sqrt{\alpha^2(l+\frac{1}{2})^2 + \alpha\beta(2m+1) + \beta^2}$

以及系数 $r_1,r_2$：

$\left\{ \begin{aligned} & r_1^{(+)} = (\frac{1}{2} + \frac{\alpha(m+\frac{1}{2}) + \beta}{2\sqrt{\alpha^2(l+\frac{1}{2})^2 + \alpha\beta(2m+1) + \beta^2}})^{1/2}\\ & r_2^{(+)} = (\frac{1}{2} - \frac{\alpha(m+\frac{1}{2}) + \beta}{2\sqrt{\alpha^2(l+\frac{1}{2})^2 + \alpha\beta(2m+1) + \beta^2}})^{1/2}\\ \end{aligned} \right.$

以及：

$\left\{ \begin{aligned} & r_1^{(-)} = -r_2^{(+)}\\ & r_2^{(-)} = r_1^{(+)}\\ \end{aligned} \right.$

对应的定态解为：

$\begin{aligned} & |\psi_{nlm_j}^{(+)}\rangle = \begin{pmatrix} r_1^{(+)} |n,l,m\rangle\\ r_2^{(+)} |n,l,m+1\rangle\\ \end{pmatrix}e^{-iE^{(+)}t/\hbar}\\ &|\psi_{nlm_j}^{(-)}\rangle = \begin{pmatrix} r_1^{(-)} |n,l,m\rangle\\ r_2^{(-)} |n,l,m+1\rangle\\ \end{pmatrix}e^{-iE^{(-)}t/\hbar}\\ \end{aligned}$

下面分情况讨论：

• $\beta \ll \alpha$
  外磁场很弱，使得自旋、轨道磁矩在外场中的能量远小于轨道-自旋耦合能量。此时有：

$E^{(\pm)} = E_{nl} + \left\{ \begin{aligned} & \frac{l}{2}\alpha + \frac{2l+2}{2l+1} (m+\frac{1}{2})\beta\\ & -\frac{l+1}{2}\alpha + \frac{2l}{2l+1} (m+\frac{1}{2})\beta\\ \end{aligned} \right.$

这称为 反常塞曼效应。

• $\beta \gg \alpha$
  此时可以将轨道-自旋耦合项当作微扰处理。可以得到：

$E^{(\pm)} = E_{nl} + \left\{ \begin{aligned} & (m+1)\beta + \frac{1}{2}m\alpha\\ & m\beta - \frac{1}{2}(m+1)\alpha\\ \end{aligned} \right.$

$\alpha = 0$ 时对应 Paschen-Back效应。

Aharonov-Bohm(AB)效应

经典力学中，描述电磁场和带电粒子运动的 Maxwell 方程和 Lorentz 力公式，都是用场强表达的。电磁势的引入只为数学上的方便，并不具有物理意义，只有在规范变换下不变的场强才有物理意义。在量子力学中，电磁场下的薛定谔方程虽然用电磁势来表示，但由于电磁势经规范变换时仅仅导致波函数多一个相因子。

因此人们一直认为在量子力学中，也如同在经典力学中一样，只有电磁场的场强才具有可观测的物理效应，电磁势不具有可观测的物理效应。但是，1959 年 Aharonor 和 Bohm 提出在量子力学中，电磁势有直接的可观测的物理效应$^{[1]}$。

下面考虑磁 AB 效应。考虑让电子双缝干涉实验，在屏后放一个无限长螺线管，磁场被完全限制在螺线管内。按照静电理论，螺线管外无磁场，并不受到力作用，加上螺线管对实验结果无影响。然而，实验表明在屏上的干涉条纹出现了移动。我们现在来说明这一点。

Aharonov-Bohm(AB)效应$^{[4]}$

考虑在 $B=0,\bm{A} =0$ 的区域内运动的电子满足的薛定谔方程：

$i\hbar \frac{\partial \psi}{\partial t} = (-\frac{\hbar^2}{2m} \nabla^2 + V)\psi \tag{27}$

那么在 $B=0,\bm{A} \neq 0$ 的区域内运动的电子满足的薛定谔方程：

$i\hbar \frac{\partial \psi'}{\partial t} = (\frac{1}{2m} (\frac{\hbar}{i}\nabla +\frac{e}{c}\bm{A})^2 + V)\psi' \tag{28}$

既然这两种情况的电磁场相同，那么其磁矢势可以用一规范变换联系起来。得到：

$\begin{aligned} &\bm{A} = \nabla f \Rightarrow f = \int_{0}^{\bm{r}}\bm{A}d\bm{r}'\\ &\quad \psi' = \psi e^{-\frac{ie}{\hbar c}f} \end{aligned}\tag{29}$

如此两缝的电子波函数干涉的波函数为：

$\begin{aligned} |\psi'_1 + \psi'_2|^2 &= | \exp(-\frac{ie}{\hbar c}f_1)\psi_1 + \exp(-\frac{ie}{\hbar c}f_2)\psi_2|^2\\ &= |\psi_1 + \exp(-\frac{ie}{\hbar c}(f_1-f_2))\psi_2|^2\\ &= |\psi_1 + \exp(-\frac{ie}{\hbar c}\oint \bm{A}(\bm{r'})d\bm{r}')\psi_2|^2\\ \end{aligned}$

额外的相位差与围住的磁通量成正比：

$\Delta \phi = \frac{e}{\hbar c}\oint \bm{A}(\bm{r'})d\bm{r}' = \frac{\Phi}{\hbar c/e}\tag{30}$

参考资料

1. 张永德 量子力学讲义
2. 规范场论. (2020, June 8). Retrieved from 维基百科, 自由的百科全书: https://zh.wikipedia.org/w/index.php?title=规范场论&oldid=60003827
3. 沈瑞 南京大学 量子力学课件
4. 由Sebastian Schmittner - 自己的作品，CC BY-SA 3.0，https://commons.wikimedia.org/w/index.php?curid=15300586