一维定态问题

Schrödinger 方程为（坐标表象）：

iℏ∂ψ(x,t)∂t=(−ℏ22μ∇2+V(x))ψ(x,t)(1)i\hbar\frac{\partial \psi(\bm{x},t)}{\partial t} = (-\frac{\hbar^2}{2\mu}\nabla^2 + V(\bm{x})) \psi(\bm{x},t)\tag{1}

在一维情况下，有：

iℏ∂ψ(x,t)∂t=−ℏ22μd2ψ(x,t)dx2+V(x)ψ(x,t)(2)i\hbar\frac{\partial\psi(x,t)}{\partial t} = -\frac{\hbar^2}{2\mu}\frac{d^2\psi(x,t)}{dx^2}+ V(x)\psi(x,t)\tag{2}

定态 Schrödinger 方程为：

Eψ(x)=−ℏ22μd2ψ(x)dx2+V(x)ψ(x)(3)E\psi(x) = -\frac{\hbar^2}{2\mu}\frac{d^2\psi(x)}{dx^2}+ V(x)\psi(x)\tag{3}

一维定态问题转化为对方程 (3)(3) 的求解。

束缚态问题

量子力学中，如果一个粒子在某势场中被约束在一个或几个空间区域内，则称粒子处于 束缚态（bound state）。如果势场在无穷远处趋于零，则负能量态一定是束缚态。束缚态粒子的能谱是离散的，而自由粒子的能谱是连续的[1]^{[1]}。

对于束缚态有 ψ(±∞)=0\psi(\pm\infty) = 0，由此

∫−∞∞ψ∗(x)ψ(x)dx<∞\int_{-\infty}^{\infty} \psi^*(x)\psi(x)dx < \infty

此时的归一化是容易进行的。利用归一化后的波函数，根据量子力学的哥本哈根诠释，发现粒子位置在 [a,b][a,b] 内的概率为：

P(x∈[a,b])=∫abψ∗(x)ψ(x)dxP(x\in[a,b]) = \int_{a}^{b}\psi^*(x)\psi(x)dx

下面以无限深方势阱为例。

无限深方势阱

Fig1：无限深方势阱[2]^{[2]}

无限深方势阱的势能形式如下：

V(x)={00<x<L∞elsewhere(4)V(x)= \left\{ \begin{aligned} &0 \quad 0 < x <L\\ &\infty \quad elsewhere\\ \end{aligned} \right.\tag{4}

在边界处，V→∞,ψ=0V\rightarrow \infty,\psi = 0。波函数被限制在 [0,L][0,L] 上。得到边界条件：

{ψ(0)=0ψ(L)=0(5)\left\{ \begin{aligned} \psi(0) = 0\\ \psi(L) = 0\\ \end{aligned} \right.\tag{5}

ψ(x)\psi(x) 在 [0,L][0,L] 外为零。因此，我们只用关心在 [0,L][0,L] 上的 Schrödinger 方程：

Eψ(x)=−ℏ22μd2ψ(x)dx2(6)E\psi(x) = -\frac{\hbar^2}{2\mu}\frac{d^2\psi(x)}{dx^2}\tag{6}

其中 E⩾Vmin=0E\geqslant V_{min} = 0。由此可得满足方程 (6)(6) 与边界条件 (5)(5) 的一般解为：

ψn(x)=Asin⁡nπxL,n=1,2,⋯(7)\psi_n(x) = A\sin \frac{n\pi x}{L},n = 1,2,\cdots\tag{7}

归一化条件给出：A=2LA = \sqrt{\frac{2}{L}}。
对应的能量为：

En=n2π2ℏ22μL2(8)E_n = \frac{n^2\pi^2\hbar^2}{2\mu L^2} \tag{8}

这就是无穷深势阱的能级公式，其能量是量子化的且无简并。

散射态问题

对于 散射态 来说，其粒子运动是不受限的。这意味着 ψ(±∞)>0\psi(\pm\infty)>0，有：

∫−∞∞ψ∗(x)ψ(x)dx=∞\int_{-\infty}^{\infty} \psi^*(x)\psi(x)dx = \infty

那么其归一化是不容易定义的。平面波就是一种散射态，我们进行了 δ\delta 归一化和箱归一化。对于散射态，我们发现粒子位置在 [a,b][a,b] 内的概率为：

P(x∈[a,b])=∫abψ∗(x)ψ(x)dx∫−∞∞ψ∗(x)ψ(x)dx(9)P(x\in[a,b]) = \frac{\int_{a}^{b}\psi^*(x)\psi(x)dx}{\int_{-\infty}^{\infty}\psi^*(x)\psi(x)dx} \tag{9}

上述式子一般来说并无良好定义。两个有限区域概率的比值是有很好定义的：

P(x∈[a2,b2])P(x∈[a1,b1])=∫a2b2ψ∗(x)ψ(x)dx∫a1b1ψ∗(x)ψ(x)dx(10)\frac{P(x\in[a_2,b_2])}{P(x\in[a_1,b_1])} = \frac{\int_{a_2}^{b_2}\psi^*(x)\psi(x)dx}{\int_{a_1}^{b_1}\psi^*(x)\psi(x)dx} \tag{10}

有限高势垒

现在考虑有限高势垒对平面波的作用。

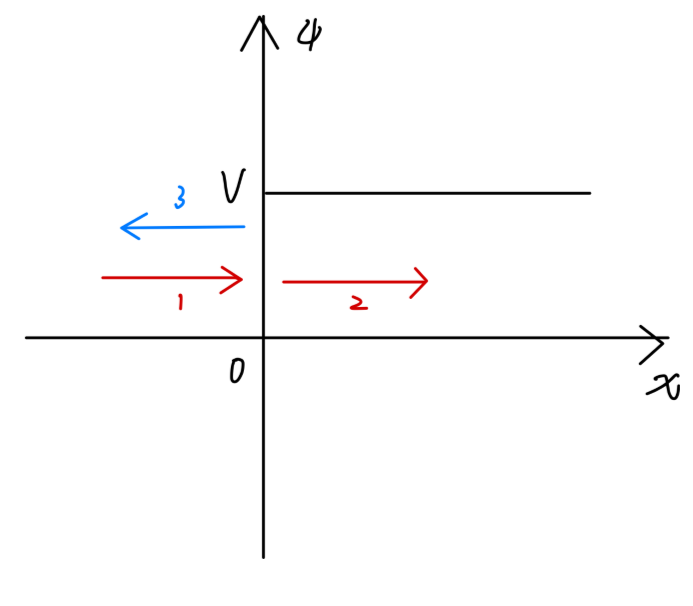
有限高势垒对平面波的反射

Fig2：有限高势垒对平面波的反射

对应的势场为：

V(x)={0x<0Vx⩾0(11)V(x) = \left\{ \begin{aligned} &0 \quad &x<0 \\ &V \quad &x\geqslant 0\\ \end{aligned} \right.\tag{11}

其中 $V_0>0 $。

在 x=0x=0 处有衔接条件：

lim⁡x→0−ψ(x)=lim⁡x→0+ψ(x),lim⁡x→0−dψ(x)dx=lim⁡x→0+dψ(x)dx\lim_{x\rightarrow 0-}\psi(x)=\lim_{x\rightarrow 0+}\psi(x),\lim_{x\rightarrow 0-}\frac{d\psi(x)}{dx}=\lim_{x\rightarrow 0+}\frac{d\psi(x)}{dx}

这对应波函数连续与概率流连续

能量有 E⩾Vmin=0E\geqslant V_{min} = 0。
在 x∈(−∞,0)x\in(-\infty,0) 的范围内，其Schrödinger 方程为：

Eψ(x)=−ℏ22μd2ψ(x)dx2(12)E\psi(x) = -\frac{\hbar^2}{2\mu}\frac{d^2\psi(x)}{dx^2}\tag{12}

其解为：

ψ(x)=Aeik1x+Be−ik1x,k1=2μEℏ2(13)\psi(x) = Ae^{ik_1x} + Be^{-ik_1x},k_1 = \sqrt{\frac{2\mu E}{\hbar^2}} \tag{13}

注意以下多次使用待定系数 A，B。这并不意味着所有的A，B的取值都是一样的，我们更多只是为了方便采取 A,BA,B 这两个特定字母表示待定系数，请结合上下文确定具体含义。

其中右边第一项对应向 xx 轴正方向传播的平面波，第二项对应向 xx 轴负方向传播的平面波。我们考虑沿着xx 轴正方向入射的平面波，对应的有一个沿着xx 轴负方向反射的平面波。

(13)(13) 可利用三角函数写为：

ψ=Asin⁡kx+Bcos⁡kx(14)\psi = A\sin kx + B\cos kx \tag{14}

在 x∈[0,+∞)x\in[0,+\infty) 的范围内，其Schrödinger 方程为：

Eψ(x)=−ℏ22μd2ψ(x)dx2+Vψ(x)(15)E\psi(x) = -\frac{\hbar^2}{2\mu}\frac{d^2\psi(x)}{dx^2}+V\psi(x)\tag{15}

现在分情况讨论：

  • 对于 0⩽E⩽V0\leqslant E \leqslant V。其解为：

ψ(x)=Aek2x+Be−k2x,k2=2μ(V−E)ℏ2(16)\psi(x) = Ae^{k_2 x} + Be^{-k_2 x},k_2 = \sqrt{\frac{2\mu (V-E)}{\hbar^2}} \tag{16}

考虑到 ψ(+∞)=0\psi(+\infty) = 0，应当取：

ψ(x)=Be−k2x\psi(x) = Be^{-k_2 x}

这对应一个逐渐衰减的透射波。
(16)(16) 式对应的解也可用双曲函数写为：

ψ(x)=Asinh⁡kx+Bcosh⁡kx\psi(x) = A\sinh kx + B\cosh kx

以上使用三角/双曲函数来代替指数函数，这样将解的奇宇称部分与偶宇称部分分开。对于特定的势场、边界条件，有时波函数的奇偶性是容易确定的，此时我们直接写出波函数的奇/偶宇称解即可。

综上，我们得到的解为：

ψ(x)={Aeik1x+Be−ik1xx<0Ce−k2xx⩾0(17)\psi(x)=\left\{ \begin{aligned} & Ae^{ik_1x} + Be^{-ik_1x} &\quad x<0\\ & C e^{-k_2x} &\quad x\geqslant0 \end{aligned} \right.\tag{17}

其中：

k1=2μEℏ2,k2=2μ(V−E)ℏ2(18)k_1 = \sqrt{\frac{2\mu E}{\hbar^2}},k_2 = \sqrt{\frac{2\mu (V-E)}{\hbar^2}}\tag{18}

考虑衔接条件，有：

{A+B=Cik1(A−B)=−k2C(19)\left\{ \begin{aligned} & A+B = C \\ & ik_1(A-B) = -k_2C\\ \end{aligned} \right.\tag{19}

解得：

B=k1−ik2k1+ik2A,C=2k1k1+ik2A(20)B = \frac{k_1-ik_2}{k_1+ik_2}A,\quad C=\frac{2k_1}{k_1+ik_2} A \tag{20}

考虑分界面概率流密度：

j=Re(ψ∗v^ψ)(21)j = \mathrm{Re}(\psi^*\hat{v}\psi)\tag{21}

对于入射波 ψi\psi_i，反射波 ψr\psi_r，投射波 ψt\psi_t，分别计算得到：

ji=k1∣A∣2,jr=−k1∣A∣2,jt=0(22)j_i = k_1|A|^2,j_r = -k_1|A|^2,j_t = 0\tag{22}

我们定义 反射率 RR 与 透射率 TT 为：

R≡∣jrji∣,T≡∣jtji∣(23)R \equiv |\frac{j_r}{j_i}|,\quad T \equiv |\frac{j_t}{j_i}|\tag{23}

总有：

R+T=1(24)R+T =1 \tag{24}

这里有：

R=1,T=0(25)R = 1,T=0\tag{25}

即能量低于势垒时，入射波被完全反射，反射波相比入射波相位发生改变。

  • 对于 0⩽E⩽V0\leqslant E \leqslant V。其解为：

ψ(x)=Aeik2x+Be−ik2x,k2=2μ(E−V)ℏ2(26)\psi(x) = Ae^{ik_2 x} + Be^{-ik_2 x},k_2 = \sqrt{\frac{2\mu (E-V)}{\hbar^2}} \tag{26}

考虑到 x>0x>0 的空间中只有一个向 xx 轴正方向传播的波，综合来说，我们取解为：

ψ(x)={Aeik1x+Be−ik1xx<0Ceik2xx⩾0(27)\psi(x)=\left\{ \begin{aligned} & Ae^{ik_1x} + Be^{-ik_1x} &\quad x<0\\ & C e^{ik_2x} &\quad x\geqslant0\\ \end{aligned} \right.\tag{27}

在 x=0x = 0 处的衔接条件为：

{A+B=Cik1(A−B)=ik2C(28)\left\{ \begin{aligned} & A+B = C \\ & ik_1(A-B) = ik_2C\\ \end{aligned} \right.\tag{28}

解得：

B=k1−k2k1+k2A,C=2k1k1+k2A(29)B = \frac{k_1-k_2}{k_1+k_2}A,\quad C=\frac{2k_1}{k_1+k_2} A \tag{29}

对于入射波 ψi\psi_i，反射波 ψr\psi_r，投射波 ψt\psi_t，分别计算得到：

ji=k1∣A∣2jr=−k1(k1−k2)2(k1+k2)2∣A∣2jt=k14k1k2(k1+k2)2∣A∣2(30)\begin{aligned} &j_i = k_1|A|^2\\ &j_r = -k_1\frac{(k_1-k_2)^2}{(k_1+k_2)^2}|A|^2\\ &j_t = k_1\frac{4k_1k_2}{(k_1+k_2)^2}|A|^2\\ \end{aligned}\tag{30}

得到反射率与透射率为：

R=(k1−k2)2(k1+k2)2T=4k1k2(k1+k2)2(31)R = \frac{(k_1-k_2)^2}{(k_1+k_2)^2}\quad T=\frac{4k_1k_2}{(k_1+k_2)^2} \tag{31}

由此，我们发现，在入射波能量大于势垒能量时，同时产生入射波与反射波。随着入射波能量变大，k2→k1k_2\rightarrow k_1，反射率将减小、透射率将增大。

δ 势垒

δ 势垒

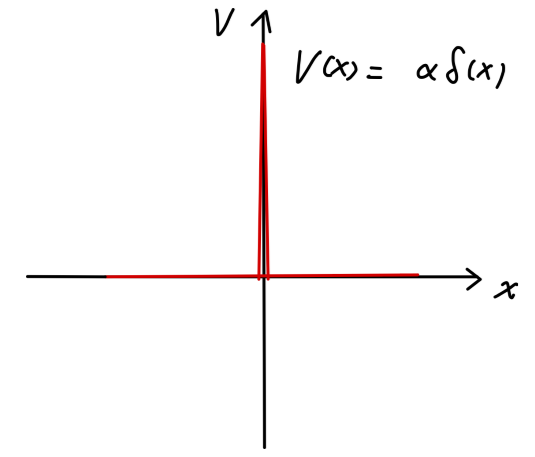
Fig3：δ\delta势垒

现在考虑 δ\delta 势垒对平面波的作用。其势函数为：

V(x)=αδ(x),α>0(32)V(x) = \alpha\delta(x),\alpha>0\tag{32}

对于 x<0x<0 以及 x>0x>0 的范围，其势能均为零。考虑一入射平面波从 x<0x<0 的区域沿着 xx 轴正方向运动，遇到 δ\delta 势垒后，产生一个透射波与反射波。由此其波函数应当为以下形式：

ψ={Aeikx+Be−ikxx<0Ceikxx>0,k=2μEℏ2(33)\psi = \left\{ \begin{aligned} & A e^{ikx} + Be^{-ikx} \quad& x<0 \\ & C e^{ikx} \quad& x>0\\ \end{aligned} \right.,k =\sqrt{\frac{2\mu E}{\hbar^2}}\tag{33}

考虑衔接条件，在 x=0x=0 处波函数时连续的。概率流也应当连续，但势函数在 x=0x=0 处发生无穷大的突变，对应的波函数在 x=0x=0 处不一定可导。如此，无法得到波函数导数连续的条件。为此，我们需要重新考虑 Schrödinger 方程，从 (3)(3) 式可得：

∫Eψ(x)dx=−∫ℏ22μdxd2ψ(x)dx2+∫V(x)ψ(x)dx\int E\psi(x)dx = -\int\frac{\hbar^2}{2\mu}dx\frac{d^2\psi(x)}{dx^2}+\int V(x)\psi(x) dx

考虑取积分区间为 [−ϵ,ϵ],ϵ>0[-\epsilon,\epsilon],\epsilon>0，由此有：

E∫−ϵϵψ(x)dx=−ℏ22μdψ(x)dx∣−ϵϵ+∫−ϵϵV(x)ψ(x)dxE\int_{-\epsilon}^{\epsilon}\psi(x)dx = -\frac{\hbar^2}{2\mu} \frac{d\psi(x)}{dx}|_{-\epsilon}^{\epsilon} + \int_{-\epsilon}^{\epsilon} V(x)\psi(x)dx

考虑到 V(x)=αδ(x)V(x) = \alpha\delta(x)，并且令 ϵ→0\epsilon\rightarrow 0，得到：

−ℏ22μΔ(dψ(x)dx)+αψ(0)=0(34)-\frac{\hbar^2}{2\mu}\Delta(\frac{d\psi(x)}{dx}) + \alpha\psi(0) = 0\tag{34}

上式就是概率流连续对应的条件。
于是我们得到这个问题中的衔接条件：

{A+B=C−ℏ22μik(C−A+B)+αC=0(35)\left\{ \begin{aligned} & A + B = C\\ & -\frac{\hbar^2}{2\mu}ik(C-A+B) + \alpha C = 0\\ \end{aligned} \right.\tag{35}

设 λ=μα/(ℏ2k)\lambda = \mu \alpha/(\hbar^2k)，得到：

B=−λi1+λiA,C=11+λiA(36)B = -\frac{\lambda i}{1+\lambda i}A, \quad C = \frac{1}{1+\lambda i}A \tag{36}

相应的可以计算反射率/透射率与相位差的改变。

周期性势

现在讨论在一维周期势中的解。一般的，周期势具有以下性质：

V(x+a)=V(x)V(x+a) = V(x)

其中 aa 为势函数的周期。对应的粒子的概率分布也具有同样的周期性：

∣ψ(x)∣2=∣ψ(x+a)∣2|\psi(x)|^2 = |\psi(x+a)|^2

由此波函数具有如下关系：

ψ(x+a)=eiθψ(x)(37)\psi(x+a) = e^{i\theta}\psi(x) \tag{37}

现在考虑势函数为 Dirac 梳的情况。所谓 Dirac 梳，其势函数为：

V(x)=−∑n=−∞∞αδ(x−na),α>0(38)V(x) = -\sum_{n=-\infty}^{\infty} \alpha \delta(x-na),\alpha>0 \tag{38}

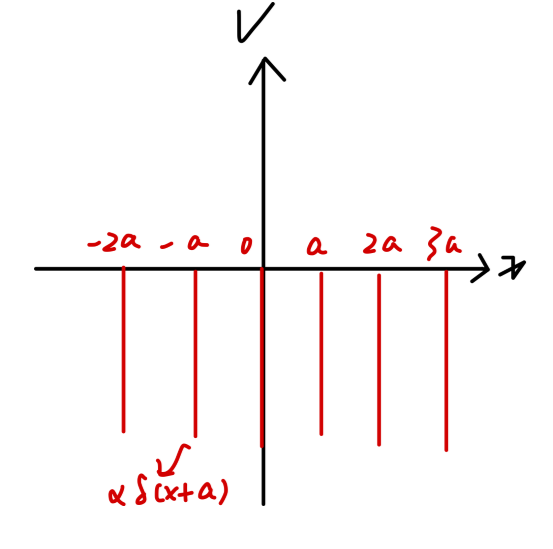
Dirac梳

Fig4：Dirac梳

那么在任意一个区间 (na,(n+1)a),n∈Z(na,(n+1)a),n\in \mathrm{Z}，其波函数是容易得到的。不失一般性的，可以选取这个区间为 (−a,0)(-a,0)，E>0E>0 的解为：

ψ(x)=Aeikx+Be−ikx,x∈(−a,0)(39)\psi(x) = A e^{ikx} + B e^{-ikx},x\in (-a,0) \tag{39}

利用 (37)(37) 可以得到 (0,a)(0,a) 上的波函数：

ψ(x)=ψ(x−a)eiθ=eiθ(Aeik(x−a)+Be−ik(x−a))(40)\begin{aligned} \psi(x)&=\psi(x-a)e^{i\theta}\\ &=e^{i\theta}( A e^{ik(x-a)} + B e^{-ik(x-a)})\\ \end{aligned}\tag{40}

结合 (39),(40)(39),(40) 式，在 x=0x =0 处考虑衔接条件：

{A+B=eiθ(Ae−ika+Beka)−ℏ22μ[ikeiθ(Ae−ika−Beka)−ik(A−B)]−α(A+B)=0\left\{ \begin{aligned} &A+ B = e^{i\theta}(Ae^{-ika} + Be^{ka})\\ &-\frac{\hbar^2}{2\mu}[ike^{i\theta}(Ae^{-ika} - Be^{ka})-ik(A-B)]-\alpha(A+B)=0 \end{aligned} \right.

作变量代换，λ=μα/(ℏ2k)\lambda = \mu \alpha/(\hbar^2k)，μ+=1−ei(θ−ka)\mu_{+} = 1-e^{i(\theta-ka)}，μ−=1−ei(θ+ka)\mu_{-} = 1-e^{i(\theta+ka)} 整理得到：

{Aμ++Bμ−=0A(−iμ++2λ)+B(iμ−+2λ)=0(41)\left\{ \begin{aligned} & A\mu_{+} + B\mu_{-} = 0\\ &A(-i\mu_{+}+2\lambda) + B(i\mu_{-}+2\lambda) = 0 \end{aligned} \right.\tag{41}

利用 (41)(41) 有解的条件，得到：

iμ−μ+=λ(μ+−μ−)i\mu_{-}\mu_{+} = \lambda(\mu_{+}-\mu_{-})

最终得到：

cos⁡θ=cos⁡ka−λsin⁡ka(42)\cos\theta = \cos ka - \lambda \sin ka \tag{42}

考虑 (42)(42) 式，左边的值域为 [−1,1][-1,1]，右边为 z=kaz =ka 的函数：

f(z)=cos⁡ka−λsin⁡ka=cos⁡ka−μαℏ2ksin⁡ka=cos⁡z−βsin⁡zz\begin{aligned} f(z) &= \cos ka - \lambda \sin ka\\ &= \cos ka - \frac{\mu \alpha}{\hbar^2 k}\sin ka \\ & = \cos z - \beta \frac{\sin z}{z} \\ \end{aligned}

其中 β\beta 只与势阱的参数有关。于是方程 (42)(42) 成为：

cos⁡θ=f(z)\cos\theta = f(z)

如果对于一个特定的 kk，存在一个对应的 θ\theta，那么该波能在该势场中传播，否则就不能。如下图，这实际上形成了 能带结构，存在 导带 与 禁带，导带之间存在带隙。能带结构是周期性势场的重要特点，固体物理讨论的对象为具有周期性结构的晶体，其势能自然是具有周期性的，我们将在固体物理的能带理论中进行详细讨论周期性势场导致的能带结构。

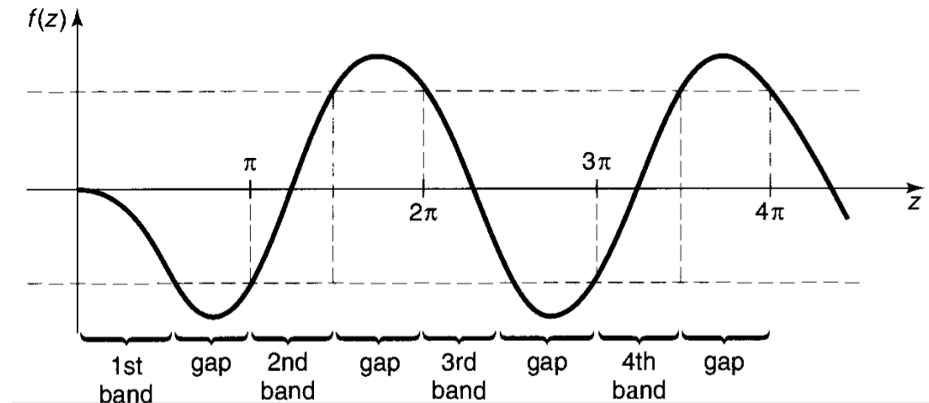
Dirac 梳的能带结构

Fig5：Dirac 梳的能带结构

简谐振子

在经典力学中，一维简谐振子的哈密顿量为：

H=p22μ+12kx2H = \frac{p^2}{2\mu}+\frac{1}{2}kx^2

对应的，在量子力学中，量子简谐振子（QSHO）满足的 Schrödinger 方程为：

iℏ∂ψ∂t=−ℏ22μ∂2ψ∂x2+12kx2(43)i\hbar\frac{\partial \psi}{\partial t} = -\frac{\hbar^2}{2\mu}\frac{\partial^2 \psi}{\partial x^2} + \frac{1}{2}kx^2 \tag{43}

定态 Schrödinger 方程为：

Eψ=−ℏ22μψ′′+12kx2ψ(44)E\psi = -\frac{\hbar^2}{2\mu}\psi'' + \frac{1}{2}kx^2\psi \tag{44}

对于方程 (44)(44) 的求解，我们介绍两种方法：级数法 与 代数法。

级数解法

考虑，在经典力学中，该谐振子对应的频率为 ω\omega，于是势能项可以写为：12μω2x2\frac{1}{2}\mu\omega^2x^2。在此基础上作以下代换：

ε=Eℏω/2,ξ=xℏ/μω(45)\varepsilon = \frac{E}{\hbar\omega/2},\quad \xi = \frac{x}{\sqrt{\hbar/\mu\omega}} \tag{45}

于是 (44)(44) 可重写为以下形式：

d2dξ2ψ(ξ)+(ε−ξ2)ψ(ξ)=0(46)\frac{d^2}{d\xi^2}\psi(\xi) + (\varepsilon-\xi^2)\psi(\xi) = 0 \tag{46}

当 ξ→∞\xi\rightarrow \infty 时，方程 (46)(46) 可以近似写为：

d2dξ2ψ(ξ)−ξ2ψ(ξ)=0\frac{d^2}{d\xi^2}\psi(\xi)-\xi^2\psi(\xi) = 0

对应的解近似为：

ψ(ξ)=Ae−ξ2/2+Beξ2/2(48)\psi(\xi) = Ae^{-\xi^2/2} + Be^{\xi^2/2} \tag{48}

(48)(48) 式启发我们可以将 ψ\psi 写为：

ψ(ξ)=h(ξ)e−ξ2/2(49)\psi(\xi) = h(\xi)e^{-\xi^2/2} \tag{49}

那么对于 ξ→∞\xi\rightarrow\infty，自然有 h(ξ)→1h(\xi)\rightarrow 1。

将 (49)(49) 代入 (46)(46) 得到关于 hh 的如下方程：

h′′−2ξh′+(ε−1)h=0(50)h''-2\xi h'+(\varepsilon-1) h = 0 \tag{50}

考虑其存在如下形式的级数解：

h(ξ)=∑n=0∞anξn(51)h(\xi) = \sum_{n=0}^{\infty} a_n\xi^n \tag{51}

代入 (46)(46) 得到：

∑n=2∞ann(n−1)ξn−2−2ξ∑n=1∞annξn−1+(ε−1)∑n=0∞anξn=0∑n=0∞[(n+2)(n+1)an+2−2nθ(n−1)an+(ε−1)an]ξn=0(52)\begin{aligned} \sum_{n=2}^{\infty} a_n n(n-1)\xi^{n-2} -2\xi\sum_{n=1}^{\infty} a_n n\xi^{n-1} + (\varepsilon-1)\sum_{n=0}^{\infty} a_n\xi^n &= 0\\ \sum_{n=0}^{\infty}[(n+2)(n+1)a_{n+2}-2n\theta(n-1)a_{n} +(\varepsilon-1)a_n ]\xi^n &= 0\\ \end{aligned}\tag{52}

其中 θ(n−2)\theta(n-2) 为单位阶跃函数。于是 (52)(52) 若成立，则等式左边 ξ\xi 的不同幂次项系数都要等于零，于是得到：

2a2+(ε−1)a0=0(n+2)(n+1)an+2+(ε−2n−1)an=0,n⩾1(53)\begin{aligned} & 2a_2 + (\varepsilon-1) a_0 = 0\\ & (n+2)(n+1)a_{n+2}+(\varepsilon-2n-1)a_n = 0,n\geqslant 1\\ \end{aligned}\tag{53}

若要求该级数不发散，那么该级数是截断的，这意味着：

∃ n∈N,s.t.ε=2n+1\exist\ n\in \mathbb{N},\quad s.t.\quad \varepsilon =2n+1

观察 (52)(52) 中的系数递推关系，我们注意到奇偶项不会同时出现，该方程将给出两个线性独立的解，分别对应奇宇称解和偶宇称解。其解就是厄密多项式 Hn(ξ)H_n(\xi)，前几个厄密多项式为：

H0(ξ)=1H1(ξ)=2ξH2(ξ)=4ξ2−2H3(ξ)=8ξ3−12ξH4(ξ)=16ξ4−48ξ2+12H5(ξ)=32ξ5−160ξ3+120ξ\begin{aligned} &H_0(\xi) = 1\\ &H_1(\xi) = 2\xi \\ &H_2(\xi) = 4\xi^2-2\\ &H_3(\xi) = 8\xi^3-12\xi\\ &H_4(\xi) = 16\xi^4-48\xi^2+12\\ &H_5(\xi) = 32\xi^5-160\xi^3+120\xi\\ \end{aligned}

考虑归一化，对应的波函数可写为：

ψn(x)=12nn!(μωπℏ)1/4Hn(ξ)e−ξ2/2(54)\psi_n(x) = \frac{1}{\sqrt{2^n n!}}(\frac{\mu\omega}{\pi\hbar})^{1/4}H_n(\xi)e^{-\xi^2/2}\tag{54}

ψ0(x)=(μωπℏ)1/4e−ξ2/2ψ1(x)=(μωπℏ)1/42ue−ξ2/2ψ2(x)=(μωπℏ)1/412(2u2−1)e−ξ2/2ψ3(x)=(μωπℏ)1/413ξ(2ξ2−3)e−ξ2/2\begin{aligned} &\psi_0(x) = (\frac{\mu\omega}{\pi\hbar})^{1/4}e^{-\xi^2/2}\\ &\psi_1(x) = (\frac{\mu\omega}{\pi\hbar})^{1/4}\sqrt{2} u e^{-\xi^2/2}\\ &\psi_2(x) = (\frac{\mu\omega}{\pi\hbar})^{1/4}\frac{1}{\sqrt{2}}(2u^2-1)e^{-\xi^2/2}\\ &\psi_3(x) = (\frac{\mu\omega}{\pi\hbar})^{1/4}\frac{1}{\sqrt{3}}\xi(2\xi^2-3)e^{-\xi^2/2}\\ \end{aligned}

计算得到相应的能级为：

En=(n+12)ℏω(55)E_n = (n+\frac{1}{2})\hbar\omega \tag{55}

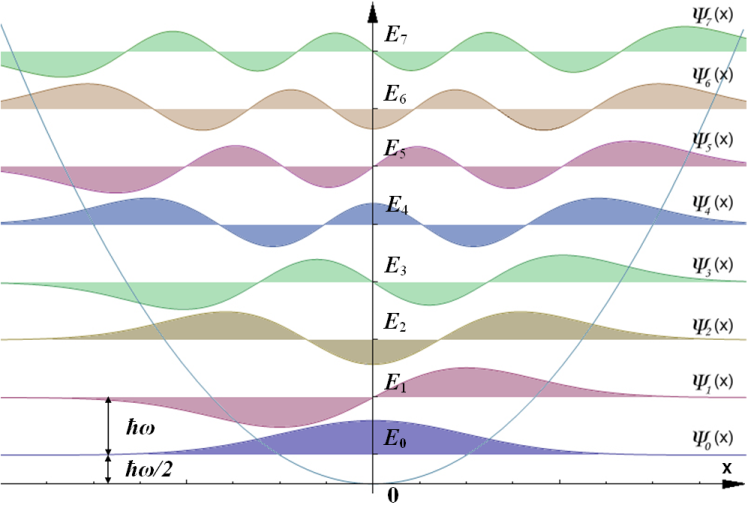
QSHO 的能级与波函数

Fig6：QSHO 的能级与波函数[3]^{[3]}

代数解法

谐振子的哈密顿算子为：

H^=12μω2x^2+12μp^2\begin{aligned} \hat{H} &= \frac{1}{2}\mu\omega^2\hat{x}^2 + \frac{1}{2\mu}\hat{p}^2\\ \end{aligned}

我们考虑以下算子：

a^=μω2ℏ(x^+iμωp^)a^†=μω2ℏ(x^−iμωp^)(56)\begin{aligned} &\hat{a} = \sqrt{\frac{\mu\omega}{2\hbar}}(\hat{x}+\frac{i}{\mu\omega}\hat{p})\\ &\hat{a}^\dagger = \sqrt{\frac{\mu\omega}{2\hbar}}(\hat{x}-\frac{i}{\mu\omega}\hat{p})\\ \end{aligned}\tag{56}

我们称这两个算子为 阶梯算子，其中 a†a^{\dagger} 为 产生算子，aa 为湮灭算子。下面考虑如何使用代数方法取求解谐振子问题。

计算对易关系：

[a^,a^†]=μω2ℏ[x^+iμωp^,x^−iμωp^]=−iℏ[x^,p^]=1(57)\begin{aligned} [\hat{a},\hat{a}^{\dagger}] &=\frac{\mu\omega}{2\hbar}[\hat{x}+\frac{i}{\mu\omega}\hat{p}, \hat{x}-\frac{i}{\mu\omega}\hat{p}]\\ &= \frac{-i}{\hbar}[\hat{x},\hat{p}]\\ & = 1\\ \end{aligned}\tag{57}

计算乘积：

a^†a^=μω2ℏ(x^−iμωp^)(x^+iμωp^)=μω2ℏ(x^2+1μ2ω2p^2+iμω[x^,p^])=μω2ℏ(x^2+1μ2ω2p^2−ℏμω)(58)\begin{aligned} \hat{a}^{\dagger}\hat{a} &= \frac{\mu\omega}{2\hbar}(\hat{x}-\frac{i}{\mu\omega}\hat{p})(\hat{x}+\frac{i}{\mu\omega}\hat{p})\\ &= \frac{\mu\omega}{2\hbar}(\hat{x}^2 + \frac{1}{\mu^2\omega^2}\hat{p}^2 + \frac{i}{\mu\omega}[\hat{x},\hat{p}])\\ &= \frac{\mu\omega}{2\hbar}(\hat{x}^2 + \frac{1}{\mu^2\omega^2}\hat{p}^2 - \frac{\hbar}{\mu\omega})\\ \end{aligned}\tag{58}

于是可以将哈密顿算子使用阶梯算子表示：

H^=(12+a^†a^)ℏω(59)\hat{H} = (\frac{1}{2}+\hat{a}^{\dagger}\hat{a})\hbar\omega\tag{59}

我们首先考虑算子 n^=a^†a^\hat{n} = \hat{a}^\dagger\hat{a}，设其本征值为 nn 的本征态为 ∣n⟩|n\rangle，即：

a^†a^∣n⟩=n^∣n⟩=n∣n⟩\hat{a}^\dagger\hat{a}|n\rangle = \hat{n}|n\rangle = n|n\rangle

我们现在考虑 n^\hat{n} 对 a^†∣n⟩\hat{a}^\dagger|n\rangle 的作用：

n^a^†∣n⟩=a^†a^a^†∣n⟩=a^†(a^†a^+1)∣n⟩=a^†(n+1)∣n⟩=(n+1)a^†∣n⟩\begin{aligned} \hat{n}\hat{a}^\dagger|n\rangle & =\hat{a}^\dagger\hat{a}\hat{a}^\dagger|n\rangle\\ & = \hat{a}^\dagger(\hat{a}^\dagger\hat{a} + 1)|n\rangle\\ & = \hat{a}^\dagger(n + 1)|n\rangle\\ & = (n + 1)\hat{a}^\dagger|n\rangle\\ \end{aligned}

由此我们发现，a^†∣n⟩\hat{a}^\dagger|n\rangle 其实是 n^\hat{n} 的本征值为 n+1n+1 的本征态，在级数解法中，我们已经发现能级是非简并的，因此，有如下关系：

a^†∣n⟩=α∣n+1⟩\hat{a}^\dagger|n\rangle = \alpha | n+1\rangle

α\alpha 为归一化系数。可以由下式求得：

∣α∣2=⟨n+1∣α∗α∣n+1⟩=⟨n∣a^a^†∣n⟩=⟨n∣a^†a^+1∣n⟩=(n+1)⟨n∣n⟩=n+1\begin{aligned} |\alpha|^2 & = \langle n+1 |\alpha^*\alpha|n+1 \rangle\\ & = \langle n|\hat{a}\hat{a}^\dagger|n\rangle \\ &= \langle n|\hat{a}^\dagger\hat{a}+1|n\rangle \\ & = (n+1) \langle n|n\rangle \\ & = n+1\\ \end{aligned}

由此得到：

a^†∣n⟩=n+1∣n+1⟩(60)\hat{a}^\dagger|n\rangle = \sqrt{n+1}|n+1\rangle\tag{60}

类似的，对于湮灭算子，同样有：

a^∣n⟩=n∣n−1⟩(61)\hat{a}|n\rangle = \sqrt{n}|n-1\rangle\tag{61}

因此现在产生算子与湮灭算子的含义就很形象了，产生算子作用后本征值加1，湮灭算子作用后本征值加1。在量子场论中，这就对应于产生一个粒子和湮灭一个粒子。对于 (61)(61) 式，我们发现 n=0n=0 时，有：

a^∣0⟩=0(62)\hat{a}|0\rangle = 0 \tag{62}

我们称 ∣0⟩|0\rangle 为 真空态，它是本征值为零的态。考虑任何其他的、本征值为 nn 的态，都能从真空态出发，通过产生算子构造出来：

∣n⟩=(a†)nn!∣0⟩(63)|n\rangle = \frac{(a^\dagger)^n}{\sqrt{n!}}|0\rangle \tag{63}

回到 (59)(59) 式，有：

H^∣n⟩=(12+n^)ℏω∣n⟩=(12+n)ℏω∣n⟩\begin{aligned} \hat{H}|n\rangle & = (\frac{1}{2}+\hat{n})\hbar\omega|n\rangle \\ & = (\frac{1}{2}+n)\hbar\omega |n\rangle \\ \end{aligned}

于是立即得到了简谐振子的能级：

En=(12+n)ℏω,n=0,1,2,⋯E_n = (\frac{1}{2}+n)\hbar\omega,\quad n = 0,1,2,\cdots

基态波函数由 (62)(62) 决定：

μω2ℏ(x^+iμωp^)ψ0=0ψ0(x)=(μωπℏ)1/4e−ξ2/2\begin{aligned} \sqrt{\frac{\mu\omega}{2\hbar}}(\hat{x}+\frac{i}{\mu\omega}\hat{p})\psi_0 = 0\\ \psi_0(x) = (\frac{\mu\omega}{\pi\hbar})^{1/4}e^{-\xi^2/2}\\ \end{aligned}

其余能级的波函数均可以从 (63)(63) 得到。

这种代数方法是很巧妙的，也具有着深刻的物理意义，在量子场论中，我们将依靠阶梯算子进行二次量子化，将谐振子的能级 nn 解释为填充在频率为 ω\omega 的振动模式上的玻色子数目。

一维定态的一般性质

上一篇讨论了多个一维定态问题，这一篇总结一下一维薛定谔方程所具有的一般性质[5]^{[5]}。

  • 本征函数族完备性定理
    一维哈密顿量 H=p22μ+V(x)H = \frac{p^2}{2\mu}+V(x) 中，若 V(x)V(x) 在任意态中的平均值有下界，那么此哈密顿量的本征函数族是完备的。

  • 在一维哈密顿量中，若非常数势 V(x)V(x) 满足：

    • V(±∞)=0V(\pm\infty)=0
    • V(x)⩽0V(x)\leqslant 0
    • ∀ ψ(x), ∃ c, s.t. ∫Vψ(x)ψ(x)∗dx⩾c\forall\ \psi(x),\ \exist\ c,\ s.t.\ \int V\psi(x)\psi(x)^*dx\geqslant c，则此系统至少存在一个束缚定态。

  • 无简并定理
    若一维势 V(x)V(x) 在有限 xx 处无奇点，则对应的全部束缚态都是不简并的，也就是说，一维问题的分立能级均无简并。

    证明：考虑两个束缚态 ψ1,ψ2\psi_1,\psi_2，均对应同一分立能级 EE，则：

    {ψ1′′=−2mℏ2(E−V)ψ1ψ2′′=−2mℏ2(E−V)ψ2 \left \{ \begin{aligned} & \psi_1'' = -\frac{2m}{\hbar^2}(E-V)\psi_1\\ & \psi_2'' = -\frac{2m}{\hbar^2}(E-V)\psi_2\\ \end{aligned} \right.

    由此不难得到：

    ψ2ψ1′′−ψ1ψ2′′=0 \psi_2\psi_1''-\psi_1\psi_2''=0

    等价于：

    ψ2ψ1′−ψ1ψ2′=const \psi_2\psi_1' - \psi_1\psi_2' = \mathrm{const}

    再进行一次积分得到：

    ln⁡ψ1=ln⁡ψ2+c \ln \psi_1 = \ln \psi_2 + c

    于是得到：

    ψ1=cψ2 \psi_1 = c\psi_2

    cc 为一个常数。于是这两个态应当代表同一个束缚定态。该理论有一个简单的推论：一维束缚态波函数总可以取成实函数。

  • 零点定理
    如果将一维问题的分立谱波函数 ψn(x)\psi_n(x) 按其本征值递增顺序编号，则属于第 n+1n+1 个能级 EnE_n 的本征函数 ψn(x)\psi_n(x)，在其定义域内有限 xx 处共有 nn 个零点。

一维含时演化问题

对于 H^\hat{H} 的每个能量为 EnE_n 的本征态 ψn\psi_n，由薛定谔方程确定其随时间演化的规律为：

ψn(t)=ψn(0)e−iEntℏ(64)\psi_n(t) = \psi_n(0)e^{-\frac{iE_nt}{\hbar}}\tag{64}

H^\hat{H} 的所有本征函数构成一组完备基。任意的波函数都可以用这组基底展开：

ψ(0)=∑nanψn(0)(65)\psi(0) = \sum_{n}a_n\psi_n(0)\tag{65}

其中每一个分量都按照 (1)(1) 所确定的规律演化，那么在 tt 时刻的波函数为：

ψ(t)=∑nanψn(0)e−iEntℏ(66)\psi(t) = \sum_{n}a_n\psi_n(0)e^{-\frac{iE_nt}{\hbar}}\tag{66}

下面我们对一些特定系统中波函数的演化作一些讨论。

二能级系统的演化

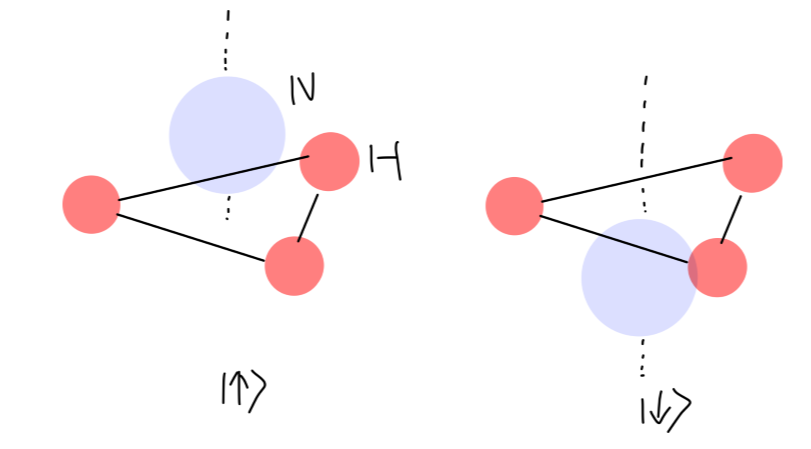
氨分子的两种构象

Fig7：氨分子的两种构象

考虑氨分子的几何构型[6]^{[6]}，相对于氢原子平面，氮原子存在一对镜像对称的可能位置。这对应两个量子态 ∣↑⟩|\uparrow\rangle，∣↓⟩|\downarrow\rangle。这两种等价的构像构成了一组基底：

∣↑⟩=(10),∣↓⟩=(01)|\uparrow\rangle = \begin{pmatrix} 1 \\ 0 \end{pmatrix},\quad |\downarrow\rangle = \begin{pmatrix} 0 \\ 1 \end{pmatrix}

氮原子要穿过氢原子平面到对称的位置需要跨过一个势垒，存在不等于零的隧穿概率，这对应哈密顿量存在非对角元。综合考虑，哈密顿量可以写为：

H=(E0−A−AE0)A>0(67)H = \begin{pmatrix} E_0 & -A\\ -A & E_0\\ \end{pmatrix}\quad A>0 \tag{67}

此时的哈密顿量的本征值和对应的本征态为：

λ1=E0+A,∣0⟩=12(1−1)λ2=E0−A,∣1⟩=12(11)(68)\begin{aligned} &\lambda_1 = E_0 + A,\quad &|0\rangle = \frac{1}{\sqrt{2}}\begin{pmatrix} 1 \\ -1\end{pmatrix}\\ &\lambda_2 = E_0 - A,\quad &|1\rangle = \frac{1}{\sqrt{2}}\begin{pmatrix} 1 \\ 1\end{pmatrix}\\ \end{aligned}\tag{68}

这是一个二能级系统，其有两个能量为 E0+A,E0−AE_0+A,E_0-A 的本征态 ∣0⟩,∣1⟩|0\rangle,|1\rangle。假设初始时（t=0t=0）系统位于如下叠加态：

ψ(0)=12∣0⟩+12∣1⟩(69)\psi(0) = \frac{1}{\sqrt{2}}|0\rangle + \frac{1}{\sqrt{2}}|1\rangle \tag{69}

则根据薛定谔方程，tt 时刻的波函数为：

ψ(t)=12e−i(E0+A)tℏ∣0⟩+12e−i(E0−A)tℏ∣1⟩(70)\psi(t) = \frac{1}{\sqrt{2}}e^{-\frac{i(E_0+A)t}{\hbar}}|0\rangle+\frac{1}{\sqrt{2}}e^{-\frac{i(E_0-A)t}{\hbar}}|1\rangle\tag{70}

若在 tt 时刻对波函数选取 {∣↑⟩,∣↓⟩}\{|\uparrow\rangle,|\downarrow\rangle \} 为基底进行测量，得到的结果为 ∣↑⟩|\uparrow\rangle 或者 ∣↓⟩|\downarrow\rangle 的概率为：

P(∣↑⟩,t)=∣⟨↑∣ψ(t)⟩∣2=∣12(⟨0∣+⟨1∣)(12e−i(E0+A)tℏ∣0⟩+12e−i(E0−A)tℏ∣1⟩)∣2=cos⁡2AtℏP(∣↓⟩,t)=∣⟨↓∣ψ(t)⟩∣2=∣12(⟨0∣−⟨1∣)(12e−i(E0+A)tℏ∣0⟩+12e−i(E0−A)tℏ∣1⟩)∣2=sin⁡2Atℏ(71)\begin{aligned} P(|\uparrow\rangle,t) &= |\langle \uparrow|\psi(t)\rangle|^2\\ & = |\frac{1}{\sqrt{2}}(\langle 0|+\langle 1|)(\frac{1}{\sqrt{2}}e^{-\frac{i(E_0+A)t}{\hbar}}|0\rangle+\frac{1}{\sqrt{2}}e^{-\frac{i(E_0-A)t}{\hbar}}|1\rangle)|^2\\ &=\cos^2\frac{At}{\hbar}\\ P(|\downarrow\rangle,t) &= |\langle \downarrow|\psi(t)\rangle|^2\\ & = |\frac{1}{\sqrt{2}}(\langle 0|-\langle 1|)(\frac{1}{\sqrt{2}}e^{-\frac{i(E_0+A)t}{\hbar}}|0\rangle+\frac{1}{\sqrt{2}}e^{-\frac{i(E_0-A)t}{\hbar}}|1\rangle)|^2\\ &=\sin^2\frac{At}{\hbar}\\ \end{aligned}\tag{71}

该结果显示，系统在 ∣↑⟩|\uparrow\rangle 与 ∣↓⟩|\downarrow\rangle 之间发生振荡。

自由高斯波包的演化

这里以高斯波包自由运动为例计算波函数随时间的演化[5]^{[5]}。
初始时刻给定高斯型波包：

ψ(x,0)=1(2πσ2)1/4e−x22σ2(72)\begin{aligned} \psi(x,0) = \frac{1}{(2\pi\sigma^2)^{1/4}}e^{-\frac{x^2}{2\sigma^2}}\tag{72} \end{aligned}

为了计算高斯波包的函数演化，我们首先要使用自由空间中的哈密顿算子 H^=12μp^2\hat{H} = \frac{1}{2\mu}\hat{p}^2 的本征态——平面波 ∣p⟩|p\rangle进行展开，我们这里选取 δ\delta-归一化的平面波函数：

ψp(x)=⟨x∣p⟩=12πℏeipxℏ(73)\psi_p(x) = \langle x|p\rangle = \frac{1}{\sqrt{2\pi\hbar}} e^{\frac{ipx}{\hbar}} \tag{73}

使用平面波将 (72)(72) 中的波函数展开为以下形式：

ψ(x,0)=⟨x∣ψ⟩=⟨x∣(∫dp∣p⟩⟨p∣)∣ψ⟩=∫⟨x∣p⟩⟨p∣ψ⟩dp=∫cpψp(x)dp(74)\begin{aligned} \psi(x,0) &= \langle x|\psi\rangle \\ &= \langle x|(\int dp |p\rangle\langle p|) |\psi\rangle\\ &=\int \langle x| p \rangle \langle p |\psi\rangle dp\\ &= \int c_p \psi_p(x) dp\\ \end{aligned}\tag{74}

其中叠加系数为：

cp=⟨p∣ψ⟩=∫⟨p∣x⟩⟨x∣ψ⟩dx=∫12πℏe−ipxℏψ(x,0)dx=12πℏ(2πσ2)1/4∫exp⁡(−ipxℏ−x22σ2)dx=12πℏ(2πσ2)1/4∫exp⁡(−12σ2(x+iσ2pℏ)2)exp⁡(−σ2p22ℏ2)dx=exp⁡(−σ2p22ℏ2)12πℏ(2πσ2)1/4(2πσ2)1/2=1(2πσp2)1/4e−p22σp2,σp=σℏ(75)\begin{aligned} c_p &=\langle p|\psi\rangle \\ &= \int \langle p|x\rangle \langle x|\psi\rangle dx\\ & = \int \frac{1}{\sqrt{2\pi\hbar}} e^{-\frac{ipx}{\hbar}}\psi(x,0) dx\\ & = \frac{1}{\sqrt{2\pi\hbar}(2\pi\sigma^2)^{1/4}} \int \exp(-i\frac{px}{\hbar}-\frac{x^2}{2\sigma^2})dx\\ & = \frac{1}{\sqrt{2\pi\hbar}(2\pi\sigma^2)^{1/4}} \int \exp(-\frac{1}{2\sigma^2}(x+\frac{i\sigma^2p}{\hbar})^2)\exp(-\frac{\sigma^2 p^2}{2\hbar^2}) dx\\ &= \exp(-\frac{\sigma^2 p^2}{2\hbar^2})\frac{1}{\sqrt{2\pi\hbar}(2\pi\sigma^2)^{1/4}} (2\pi\sigma^2)^{1/2}\\ & = \frac{1}{(2\pi\sigma_p^2)^{1/4}} e^{-\frac{p^2}{2\sigma_p^2}},\quad \sigma_p = \frac{\sigma}{\hbar} \end{aligned}\tag{75}

其实 cpc_p 就是 ∣ψ⟩|\psi\rangle 在动量表象下的波函数。我们发现对于高斯波包（坐标表象）来说，在动量表象中也为一个高斯波包。对于每一个平面波来说，对应的能量为 p2/(2μ)p^2/(2\mu)，随时间演化的规律为：

ψp(x,t)=⟨x∣p⟩=12πℏei(px−Et)ℏ(76)\psi_p(x,t) = \langle x|p\rangle = \frac{1}{\sqrt{2\pi\hbar}} e^{\frac{i(px-Et)}{\hbar}} \tag{76}

于是得到高斯波包自由演化到 tt 时刻的波函数为：

ψ(x,t)=∫cpψp(x)e−iEtℏdp=∫1(2πσp2)1/4e−p22σp212πℏei(px−Et)ℏdp=1(2πσp2)1/412πℏ∫exp⁡(−p22σp2+i(px−Et)ℏ)dp=1(2πσp2)1/412πℏ∫exp⁡(−x22(σ2+iℏtμ))exp⁡(−(12σp2+it2μℏ))dp=1(2πσp2)1/412πℏexp⁡(−x22(σ2+iℏtμ))(2π1σp2+itμℏ)12=1(2π(σ+itℏμ)2)1/4exp⁡(−x22(σ2+iℏtμ))=1(2πσt2)1/4exp⁡(−x22σt2)\begin{aligned} \psi(x,t) &= \int c_p\psi_p(x)e^{-i\frac{Et}{\hbar}}dp\\ & = \int \frac{1}{(2\pi\sigma_p^2)^{1/4}} e^{-\frac{p^2}{2\sigma_p^2}}\frac{1}{\sqrt{2\pi\hbar}} e^{\frac{i(px-Et)}{\hbar}}dp\\ &= \frac{1}{(2\pi\sigma_p^2)^{1/4}}\frac{1}{\sqrt{2\pi\hbar}} \int \exp(-\frac{p^2}{2\sigma_p^2}+\frac{i(px-Et)}{\hbar})dp\\ &=\frac{1}{(2\pi\sigma_p^2)^{1/4}}\frac{1}{\sqrt{2\pi\hbar}} \int \exp(-\frac{x^2}{2(\sigma^2+\frac{i\hbar t}{\mu})})\exp(-(\frac{1}{2\sigma_p^2}+\frac{it}{2\mu\hbar}))dp\\ &=\frac{1}{(2\pi\sigma_p^2)^{1/4}}\frac{1}{\sqrt{2\pi\hbar}}\exp(-\frac{x^2}{2(\sigma^2+\frac{i\hbar t}{\mu})})(\frac{2\pi}{\frac{1}{\sigma_p^2}+\frac{it}{\mu\hbar}})^{\frac{1}{2}}\\ &=\frac{1}{(2\pi(\sigma+\frac{it\hbar}{\mu})^2)^{1/4}} \exp(-\frac{x^2}{2(\sigma^2+\frac{i\hbar t}{\mu})})\\ &=\frac{1}{(2\pi\sigma_t^2)^{1/4}} \exp(-\frac{x^2}{2\sigma_t^2})\\ \end{aligned}

随着时间不断演化，∣σt∣|\sigma_t| 逐渐变大，高斯波包弥散开来。

参考资料

  1. Liboff, Richard L. Introductory Quantum Mechanics. Addison-Wesley. 2002. ISBN 0-8053-8714-5.
  2. 由Infinite_potential_well.svg: Bdeshamderivative work: Papa November (talk) - Infinite_potential_well.svg，CC BY-SA 3.0，https://commons.wikimedia.org/w/index.php?curid=7699138
  3. 由AllenMcC. - File:HarmOsziFunktionen.jpg，CC BY-SA 3.0，https://commons.wikimedia.org/w/index.php?curid=11623546
  4. 沈瑞 南京大学 量子力学课件
  5. 张永德 中国科学技术大学 量子力学讲义
  6. 赵凯华 新概念物理 量子物理