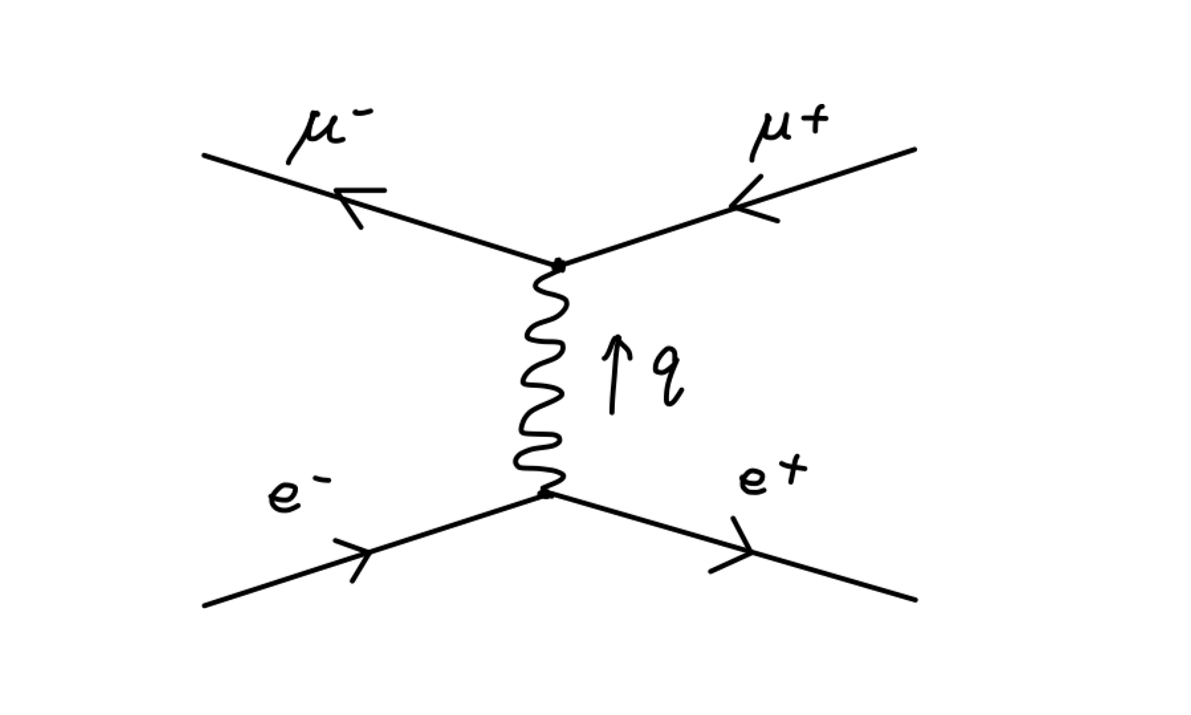
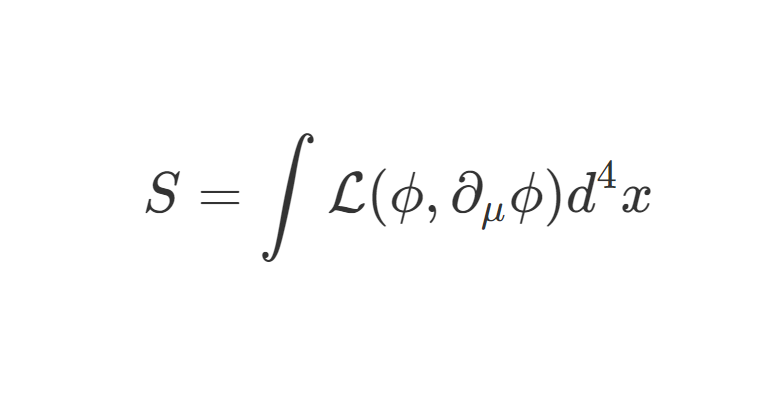在前两篇中，我们讨论了 tree-level 的费曼图。我们现在考虑一个电子和一个其他质量较大粒子的散射过程

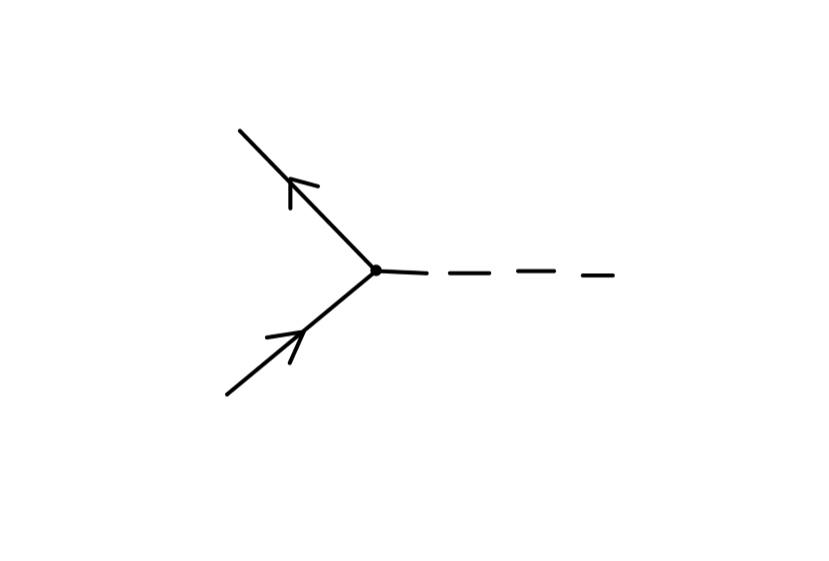
我们现在考虑这个 QED 顶点：

根据费曼规则，其值为：

−ieγμ-ie\gamma^{\mu}

我们现在考虑对这个 QED 顶点做修正得到一阶费曼图，一共有 4 种方法：

  • external leg correction
  • 真空极化 vacuum polarization
  • 顶点修正 vertex correction

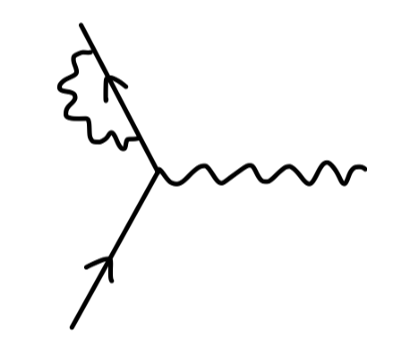
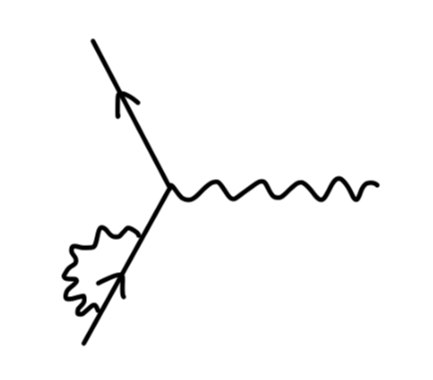
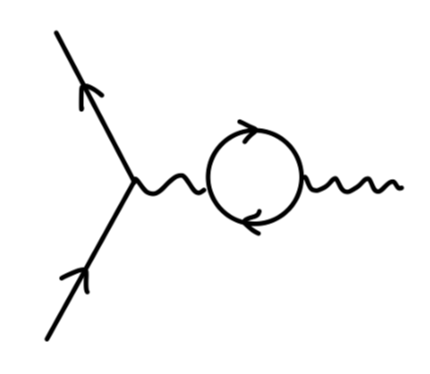
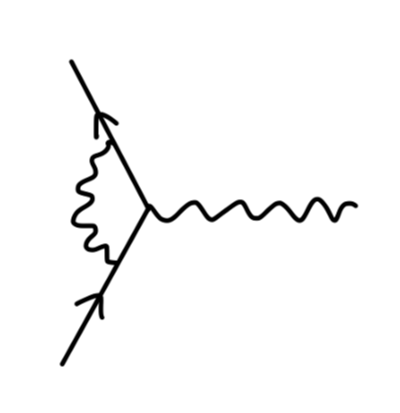
对于 external leg correction，我们说他并不是 amputated，在散射矩阵的计算中可以不用考虑。对于真空极化，我们将在之后一篇笔记中考虑。对于顶点修正，它使得电子存在 反常磁矩 anomalous magnetic moment。

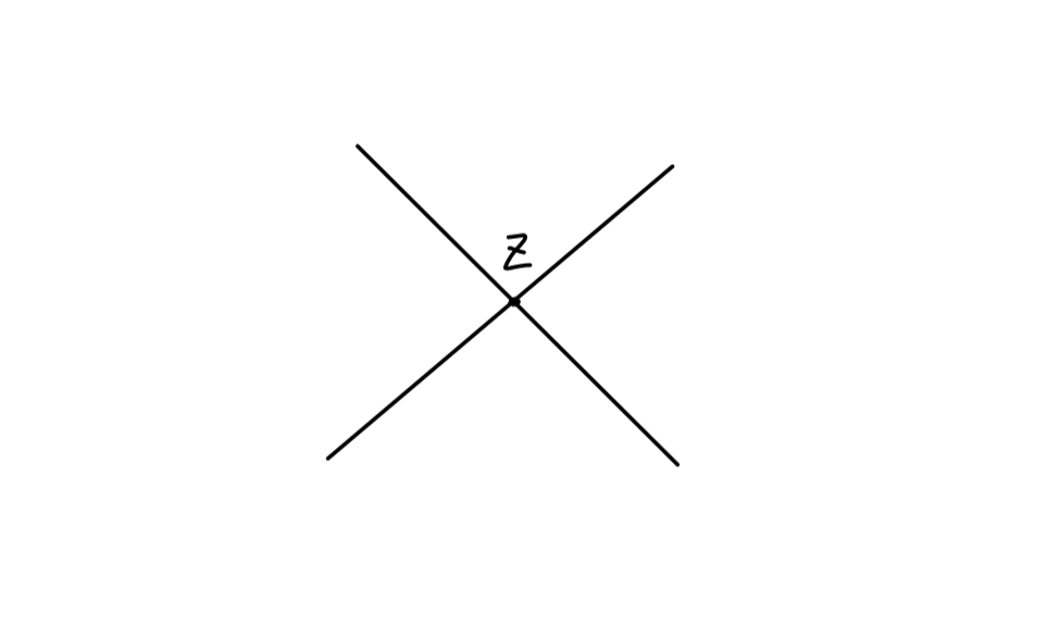
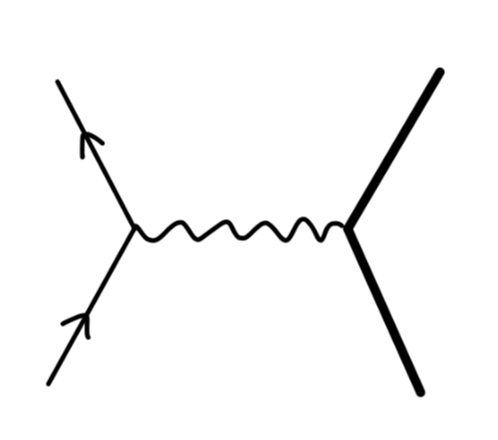
一般的顶点修正费曼图为：

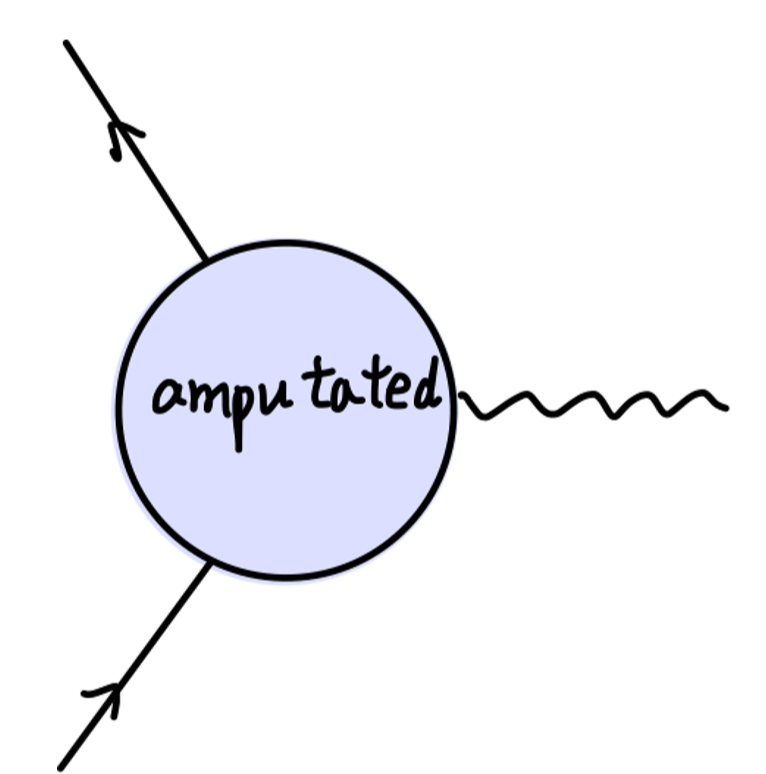
该值为：

iΓμ(p,p′)i\Gamma^{\mu}(p,p')

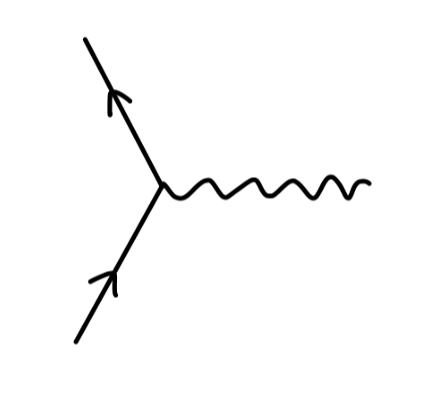
但是仅仅考虑该费曼图，该结果将在红外区发散。为了解决这件事情，我们需要考虑额外考虑如下费曼图：

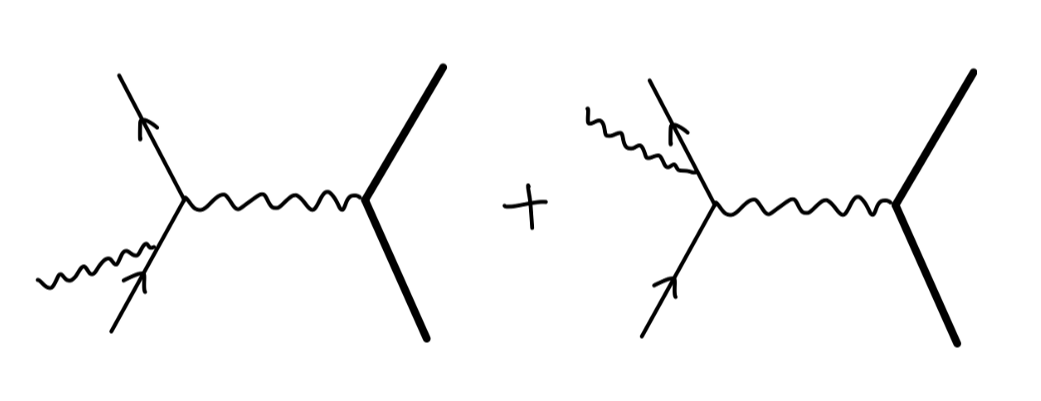
这对应于 轫致辐射 bremsstrahlung，这是本篇进行讨论的。在下一篇中，我们讨论顶点修正。

轫致辐射

轫致辐射的经典计算

考虑一个经典的电子在 t=0,x=0t=0,\bm{x}=0 时受到冲击，使得四动量从 pp 变化到 p′p'。根据电动力学，该电子将会放出辐射。现在，我们首先来进行经典的计算。

现在计算一个粒子对应的电流密度。例如，对于一个静止的粒子，有：

jμ(x)=(1,0)μ⋅eδ(3)(x)=∫dt(1,0)μ⋅eδ(4)(x−y(t))yμ(t)=(t,0)μ(1)\begin{aligned} j^{\mu}(x) &= (1,\bm{0})^{\mu} \cdot e\delta^{(3)}(\bm{x})\\ &= \int dt (1,\bm{0})^{\mu}\cdot e\delta^{(4)}(x-y(t))\qquad y^{\mu}(t) = (t,\bm{0})^{\mu}\\ \end{aligned}\tag{1}

对于一般的运动轨迹 y(τ)y(\tau)，对应的电流密度为：

jμ(x)=e∫dτdyμ(τ)dτδ(4)(x−y(τ))(2)j^{\mu}(x) = e\int d\tau \frac{dy^{\mu}(\tau)}{d\tau}\delta^{(4)}(x-y(\tau))\tag{2}

注意，上述表达式的结果是不依赖于轨迹 y(τ)y(\tau) 参数化的方式的。现在考虑轫致辐射发生的场景：在 τ<0\tau<0 时，电子以动量 pp 运动；在 τ=0\tau = 0 时，电子受到冲击；在 τ>0\tau>0 时，电子以动量 p′p' 运动。我们将 y(τ)y(\tau) 写为：

yμ(τ)={(pμ/m)ττ<0(p′μ/m)ττ>0(3)y^{\mu}(\tau) = \left\{ \begin{aligned} &(p^{\mu}/m) \tau \quad &\tau<0\\ &(p'^{\mu}/m) \tau\quad &\tau>0\\ \end{aligned} \right.\tag{3}

得到电流密度为：

jμ(x)=e∫0∞dτp′μmδ(4)(x−p′mτ)+e∫−∞0dτpμmδ(4)(x−pmτ)(4)j^{\mu}(x) = e\int_{0}^{\infty}d\tau \frac{p'^{\mu}}{m}\delta^{(4)}(x-\frac{p'}{m}\tau) + e\int_{-\infty}^{0}d\tau \frac{p^{\mu}}{m}\delta^{(4)}(x-\frac{p}{m}\tau)\tag{4}

我们对其进行傅里叶变换，为了使得积分收敛，我们需要为其添加一个指数因子：

j~μ(k)=∫d4xeik⋅xjμ(x)=e∫0∞dτp′μmei(kp′/m+iϵ)τ+e∫−∞0dτpμmei(kp/m−iϵ)τ=ie(p′μk⋅p′+iϵ−pμk⋅p−iϵ)(5)\begin{aligned} \tilde{j}^{\mu}(k) &= \int d^4x e^{ik\cdot x}j^{\mu}(x)\\ &= e\int_{0}^{\infty} d\tau \frac{p'^{\mu}}{m} e^{i(kp'/m+i\epsilon)\tau} + e\int_{-\infty}^{0} d\tau \frac{p^{\mu}}{m} e^{i(kp/m-i\epsilon)\tau}\\ &= ie(\frac{p'^{\mu}}{k\cdot p' + i\epsilon}-\frac{p^{\mu}}{k\cdot p - i\epsilon}) \end{aligned}\tag{5}

接下来我们来求解 Maxwell 方程。使用 Lorentz 规范 ∂μAμ=0\partial^{\mu}A_{\mu}=0，矢势满足波动方程：

∂2Aμ=jμ\partial^2 A^{\mu} = j^{\mu}

在频域中，上述方程成为：

A~μ(k)=−1k2j~μ(k)(6)\tilde{A}^{\mu}(k) = -\frac{1}{k^2}\tilde{j}^{\mu}(k) \tag{6}

可以解得 Aμ(x)A^{\mu}(x)：

Aμ(x)=∫d4k(2π)4e−ik⋅x−iek2(p′μk⋅p′+iϵ−pμk⋅p−iϵ)(7)A^{\mu}(x) = \int \frac{d^4k}{(2\pi)^4}e^{-ik\cdot x}\frac{-ie}{k^2}(\frac{p'^{\mu}}{k\cdot p' + i\epsilon}-\frac{p^{\mu}}{k\cdot p - i\epsilon})\tag{7}

考虑上述对 k0k^0 的复变积分。那么以上表达式的极点为：

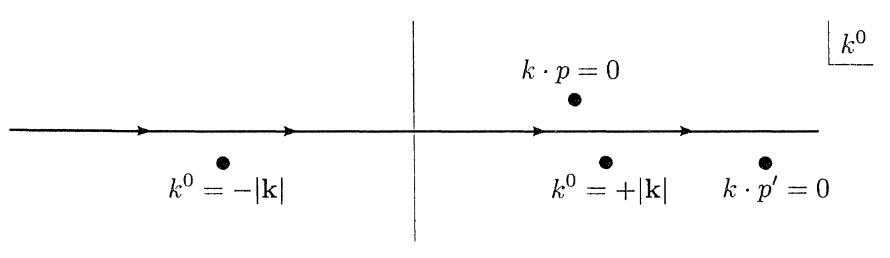
k0=−∣k∣k0=+∣k∣k⋅p=0k⋅p′=0\begin{aligned} &k^0 = -|\bm{k}|\\ &k^0 = +|\bm{k}|\\ &k \cdot p = 0\\ &k \cdot p' = 0\\ \end{aligned}

对于 t<0t<0，我们使得围线向上闭合。包含的极点为：

k0=k⋅pp0k^0 = \frac{\bm{k}\cdot\bm{p}}{p^0}

积分结果为：

Aμ(x)=∫d3k(2π)3eik⋅xe−i(k⋅p/p0)t2πi(+ie)2πk2pμp0=∫d3k(2π)3eik⋅xe−i(k⋅p/p0)t−ek2pμp0\begin{aligned} A^{\mu}(x) &= \int \frac{d^3k}{(2\pi)^3} e^{i\bm{k}\cdot \bm{x}} e^{-i(\bm{k}\cdot\bm{p}/p^0)t} \frac{2\pi i (+ie)}{2\pi k^2} \frac{p^{\mu}}{p^0}\\ &= \int \frac{d^3k}{(2\pi)^3} e^{i\bm{k}\cdot \bm{x}} e^{-i(\bm{k}\cdot\bm{p}/p^0)t} \frac{-e}{k^2} \frac{p^{\mu}}{p^0}\\ \end{aligned}

我们不妨做一些分析：若该带电粒子是静止的，pμ=(p0,0)p^{\mu} = (p^0,\bm{0})，矢势化简为：

Aμ(x)=∫d3k(2π)3eik⋅xe∣k∣2⋅(1,0)A^{\mu}(x) = \int \frac{d^3k}{(2\pi)^3} e^{i\bm{k}\cdot\bm{x}} \frac{e}{|\bm{k}|^2}\cdot(1,\bm{0})

这表示了粒子库伦势的贡献。那么对于非静止粒子的情况，极点 k⋅p/p0\bm{k}\cdot\bm{p}/p^0 自然表示其库伦势的贡献。而单单考虑库伦势是不会出现辐射的。

当 t>0t>0 时，我们选取围线向下闭合。此时围线内包含三个极点，其中极点 k0=k⋅p′/p′0k^0 = \bm{k}\cdot\bm{p}'/p'^{0} 表示出射粒子库伦势的贡献。我们重点关注剩下两个极点 k0=±∣k∣k^0 = \pm |\bm{k}| 的贡献，它们构成了辐射场：

Aradμ(x)=−∫d3k(2π)3e2∣k∣{e−ik⋅x(p′μk⋅p′−pμk⋅p)+c.c}∣k0=∣k∣=Re∫d3k(2π)3Aμ(k)e−ik⋅x(8)\begin{aligned} A^{\mu}_{rad}(x) &= -\int \frac{d^3k}{(2\pi)^3} \frac{e}{2|\bm{k}|}\{ e^{-ik\cdot x}(\frac{p'^{\mu}}{k\cdot p'}-\frac{p^{\mu}}{k\cdot p}) + c.c \}|_{k^0 = |\bm{k}|}\\ &= \mathrm{Re} \int \frac{d^3k}{(2\pi)^3}\mathcal{A}^{\mu}(\bm{k})e^{-ik\cdot x} \end{aligned}\tag{8}

其中：

Aμ(k)=−e∣k∣(p′μk⋅p′−pμk⋅p)(9)\mathcal{A}^{\mu}(\bm{k}) = \frac{-e}{|\bm{k}|}(\frac{p'^{\mu}}{k\cdot p'}-\frac{p^{\mu}}{k\cdot p})\tag{9}

为了得到辐射能量，我们需要计算电场与磁场。在频域中，有：

E(k)=−kA0(k)+ik0A(k)B(k)=ik×A(k)=k^×E(k)(10)\begin{aligned} \mathcal{E}(\bm{k}) &= -\bm{k}\mathcal{A}^0(\bm{k}) + ik^0 \mathcal{A}(\bm{k})\\ \mathcal{B}(\bm{k}) &= i\bm{k}\times\mathcal{A}(\bm{k})=\hat{k}\times\mathcal{E}(\bm{k})\\ \end{aligned}\tag{10}

得到：

E(x)=Re∫d3k(2π)3E(k)e−ik⋅xB(x)=Re∫d3k(2π)3B(k)e−ik⋅x(11)\begin{aligned} \bm{E}(x) = \mathrm{Re}\int\frac{d^3k}{(2\pi)^3} \mathcal{E}(\bm{k})e^{-ik\cdot x}\\ \bm{B}(x) = \mathrm{Re}\int\frac{d^3k}{(2\pi)^3} \mathcal{B}(\bm{k})e^{-ik\cdot x}\\ \end{aligned}\tag{11}

计算总能量：

E=12∫d3x(∣E(x)∣2+∣B(x)∣2)(12)\begin{aligned} E &= \frac{1}{2}\int d^3x (|\bm{E}(x)|^2 + |\bm{B}(x)|^2)\\ \end{aligned}\tag{12}

将 (11)(11) 式代入 (12)(12) 计算总能量，以及利用 (10)(10) 式，化简得到：

E=12∫d3k(2π)3E(k)⋅E∗(k)(13)E = \frac{1}{2}\int \frac{d^3k}{(2\pi)^3}\mathcal{E}(\bm{k})\cdot \mathcal{E}^*(\bm{k})\tag{13}

考虑到 E(k)\mathcal{E}(\bm{k}) 是横波，因此，我们引入两个横向的单位极化矢量 ϵλ(k),λ=1,2\epsilon_{\lambda}(\bm{k}),\lambda =1,2。如此：

E(k)E∗(k)=∑λ=1,2∣ϵλ(k)⋅E(k)∣2=∣k∣2∑λ=1,2∣ϵλ(k)⋅A(k)∣2\mathcal{E}(\bm{k})\mathcal{E}^*(\bm{k}) = \sum_{\lambda=1,2}|\epsilon_{\lambda}(\bm{k})\cdot\mathcal{E}(\bm{k})|^2 = |\bm{k}|^2\sum_{\lambda=1,2}|\epsilon_{\lambda}(\bm{k})\cdot\mathcal{A}(\bm{k})|^2

将式 (9)(9) 代入得到能量为：

E=12∫d3k(2π)3E(k)⋅E∗(k)=12∫d3k(2π)3∣k∣2∑λ=1,2∣ϵλ(k)⋅A(k)∣2=12∫d3k(2π)3e2∑λ=1,2∣ϵλ(k)⋅(p′k⋅p′−pk⋅p)∣2\begin{aligned} E &= \frac{1}{2}\int \frac{d^3k}{(2\pi)^3}\mathcal{E}(\bm{k})\cdot \mathcal{E}^*(\bm{k}) \\ &= \frac{1}{2}\int \frac{d^3k}{(2\pi)^3} |\bm{k}|^2\sum_{\lambda=1,2}|\bm{\epsilon}_{\lambda}(\bm{k})\cdot\mathcal{A}(\bm{k})|^2\\ &= \frac{1}{2}\int \frac{d^3k}{(2\pi)^3} e^2 \sum_{\lambda=1,2}|\bm{\epsilon}_{\lambda}(\bm{k})\cdot(\frac{\bm{p}'}{k\cdot p'}-\frac{\bm{p}}{k\cdot p})|^2\\ \end{aligned}

由于四维极化矢量的第一个分量为零。因此，我们可以将上式中的 p,p′,ϵ\bm{p},\bm{p}',\bm{\epsilon} 均用四矢量代替：

E=12∫d3k(2π)3e2∑λ=1,2∣ϵλ(k)⋅(p′k⋅p′−pk⋅p)∣2(14)E = \frac{1}{2}\int \frac{d^3k}{(2\pi)^3} e^2 \sum_{\lambda=1,2}|\epsilon_{\lambda}(\bm{k})\cdot(\frac{p'}{k\cdot p'}-\frac{p}{k\cdot p})|^2 \tag{14}

记

Mμ(k)=p′μk⋅p′−pμk⋅p\mathcal{M}^{\mu}(k) = \frac{p'^{\mu}}{k\cdot p'}-\frac{p^{\mu}}{k\cdot p}

由于：

kμMμ(k)=0k_{\mu}\mathcal{M}^{\mu}(k) = 0

不妨取类光的 kμ=(k,0,0,k)k^{\mu} = (k,0,0,k)，得到：

kM0(k)−kM3(k)=0⇒M0(k)=M3(k)k\mathcal{M}^{0}(\bm{k}) - k\mathcal{M}^{3}(\bm{k}) = 0 \Rightarrow \mathcal{M}^{0}(\bm{k}) = \mathcal{M}^{3}(\bm{k})

对应的两个横向极化矢量可以取为：

ϵ1=(0,1,0,0)ϵ2=(0,0,1,0)\epsilon_1 = (0,1,0,0)\quad \epsilon_2 = (0,0,1,0)

那么得到：

∑λ=1,2∣ϵλ(k)⋅M(k)∣2=∑λ=1,2ϵλμ(k)ϵλν∗(k)Mμ(k)Mν∗(k)=∣M1(k)∣2+∣M2(k)∣2=−∣M0(k)∣2+∣M1(k)∣2+∣M2(k)∣2+∣M3(k)∣2=−gμνMμ(k)Mν∗(k)\begin{aligned} \sum_{\lambda=1,2}|\epsilon_{\lambda}(\bm{k})\cdot\mathcal{M}(\bm{k})|^2 &= \sum_{\lambda = 1,2} \epsilon_{\lambda\mu}(\bm{k})\epsilon_{\lambda\nu}^*(\bm{k})\mathcal{M}^{\mu}(\bm{k})\mathcal{M}^{\nu*}(\bm{k})\\ &= |\mathcal{M}^1(\bm{k})|^2 + |\mathcal{M}^2(\bm{k})|^2\\ &= -|\mathcal{M}^0(\bm{k})|^2 + |\mathcal{M}^1(\bm{k})|^2 + |\mathcal{M}^2(\bm{k})|^2 + |\mathcal{M}^3(\bm{k})|^2\\ & = -g_{\mu\nu}\mathcal{M}^\mu(\bm{k})\mathcal{M}^{\nu*}(\bm{k}) \end{aligned}

这种技巧是常用的，在点乘 Mμ\mathcal{M}^{\mu} 的情况下，我们可以做如下替代：

∑ϵμϵν∗=−gμν\sum\epsilon_{\mu}\epsilon_{\nu}^{*} = -g_{\mu\nu}

回到 (14)(14) 式，我们继续得到：

E=∫d3k(2π)3e22(−gμν)(p′μk⋅p′−pμk⋅p)(p′νk⋅p′−pνk⋅p)=∫d3k(2π)3e22(−p′2(k⋅p′)2+2p⋅p′(k⋅p)(k⋅p′)−p2(k⋅p)2)=∫d3k(2π)3e22(−m2(k⋅p′)2+2p⋅p′(k⋅p)(k⋅p′)−m2(k⋅p)2)=e2(2π)2∫dkI(v,v′)(15)\begin{aligned} E &= \int \frac{d^3k}{(2\pi)^3} \frac{e^2}{2}(-g_{\mu\nu})(\frac{p'^{\mu}}{k\cdot p'}-\frac{p^{\mu}}{k\cdot p})(\frac{p'^{\nu}}{k\cdot p'}-\frac{p^{\nu}}{k\cdot p})\\ &= \int \frac{d^3k}{(2\pi)^3}\frac{e^2}{2}(-\frac{p'^2}{(k \cdot p')^2} + \frac{2p\cdot p'}{(k\cdot p)(k \cdot p')} -\frac{p^2}{(k \cdot p)^2} )\\ &= \int \frac{d^3k}{(2\pi)^3}\frac{e^2}{2}(-\frac{m^2}{(k \cdot p')^2} + \frac{2p\cdot p'}{(k\cdot p)(k \cdot p')} -\frac{m^2}{(k \cdot p)^2} )\\ &= \frac{e^2}{(2\pi)^2} \int dk \mathcal{I}(\bm{v},\bm{v}') \end{aligned}\tag{15}

我们现在想要看一看 I(v,v′)\mathcal{I}(\bm{v},\bm{v}') 的具体形式。选取一个特定参考系进行讨论：若电子的能量不变，仅仅是动量改变了方向，取：

pμ=E(1,v)p′μ=E(1,v′)kμ=(k,k)p^{\mu} = E(1,\bm{v})\quad p'^{\mu} = E(1,\bm{v}')\quad k^{\mu} = (k,\bm{k})

那么得到

I(v,v′)=∫dΩk4π(2(1−v⋅v′)(1−k^⋅v)(1−k^⋅v′)−m2/E2(1−k^⋅v′)2−m2/E2(1−k^⋅v)2)(16)\mathcal{I}(\bm{v},\bm{v}') = \int \frac{d\Omega_{k}}{4\pi} (\frac{2(1-\bm{v}\cdot\bm{v}')}{(1-\hat{k}\cdot\bm{v})(1-\hat{k}\cdot\bm{v}')} - \frac{m^2/E^2}{(1-\hat{k}\cdot \bm{v}')^2}- \frac{m^2/E^2}{(1-\hat{k}\cdot \bm{v})^2})\tag{16}

考虑到 I(v,v′)\mathcal{I}(\bm{v},\bm{v}') 并不依赖于 kk，可得能量是发散的，这并不是我们期望得到的结果。我们引入一个截断，只考虑那些频率低于散射时间倒数的辐射。如此：

E=απkmaxI(v,v′)E = \frac{\alpha}{\pi}k_{max}\mathcal{I}(\bm{v},\bm{v}')

在极端相对论情形下：对辐射能量的主要贡献来自于 (16)(16) 式第一项在两个极点附近的贡献。这里给出结果：

I(v,v′)≈2log⁡(−q2m2)\mathcal{I}(\bm{v},\bm{v}') \approx 2\log (-\frac{q^2}{m^2})

得到光子数为：

N=απ∫0kmaxdk1kI(v,v′)N = \frac{\alpha}{\pi} \int_{0}^{k_{max}} dk \frac{1}{k}\mathcal{I}(\bm{v},\bm{v}')

轫致辐射的量子计算

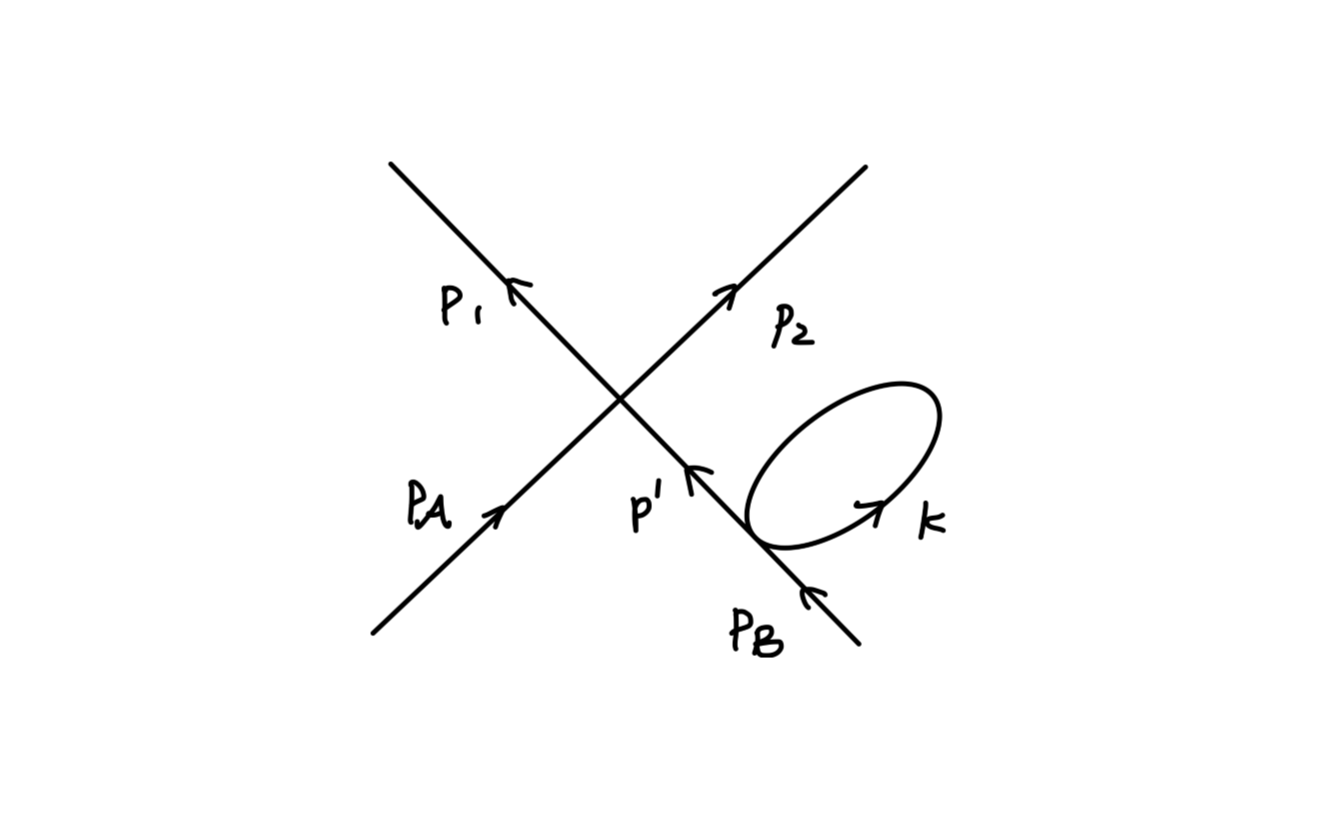
考虑轫致辐射对应的费曼图：

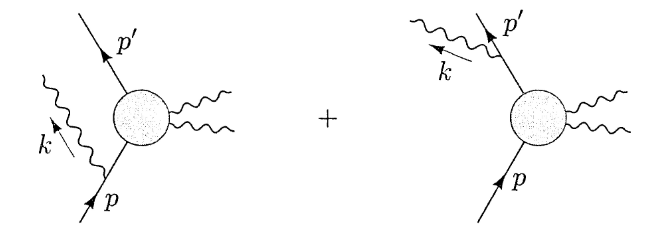
使用 M0\mathcal{M}_0 来表示电子和外场相互作用发生弹性散射的振幅。得到：

iM=ieuˉ(p′)(M0(p′,p−k)i(γ⋅(p−k)+m)(p−k)2−m2γμϵμ∗(k)+γμϵμ∗(k)i(γ⋅(p′+k)+m)(p′+k)2−m2M0(p′+k,p))u(p)≈uˉ(p′)(M0(p′,p))u(p)⋅(e(p′⋅ϵ∗p′⋅k−p⋅ϵ∗p⋅k))(17)\begin{aligned} i\mathcal{M} &= ie\bar{u}(p')(\mathcal{M}_0(p',p-k)\frac{i(\gamma\cdot(p-k)+m)}{(p-k)^2-m^2}\gamma^{\mu}\epsilon_{\mu}^*(k)\\ &\qquad +\gamma^{\mu}\epsilon_{\mu}^*(k)\frac{i(\gamma\cdot(p'+k)+m)}{(p'+k)^2-m^2}\mathcal{M}_0(p'+k,p))u(p)\\ & \approx \bar{u}(p')(M_0(p',p))u(p)\cdot(e(\frac{p'\cdot \epsilon^*}{p'\cdot k}-\frac{p\cdot \epsilon^*}{p\cdot k})) \end{aligned}\tag{17}

上述推导中使用了 soft photon 近似：∣k∣≪∣p′−p∣|\bm{k}|\ll |\bm{p}'-\bm{p}|。如此，我们可以假设：

M0(p′,p−k)≈M0(p′+k,p)≈M0(p′,p)\mathcal{M}_0(p',p-k) \approx \mathcal{M}_0(p'+k,p) \approx \mathcal{M}_0(p',p)

其次，运用了以下推导：

(γ⋅p+m)γμϵμ∗u(p)=(2pμϵμ∗+γμϵμ∗(−γ⋅p+m))u(p)=2pμϵμ∗u(p)\begin{aligned} (\gamma\cdot p + m)\gamma^{\mu}\epsilon_{\mu}^* u(p) &= (2p^{\mu}\epsilon_{\mu}^*+\gamma^{\mu}\epsilon_{\mu}^*(-\gamma\cdot p + m))u(p)\\ &=2p^{\mu}\epsilon_{\mu}^* u(p)\\ \end{aligned}

两边平方后同时对相空间积分，可以将轫致辐射的截面与弹性散射的截面关联起来：

dσ(p→p′+γ)=dσ(p→p′)⋅∫d3k(2π)312k∑λ=1,2e2∣p′⋅ϵ(λ)p′⋅k−p⋅ϵ(λ)p⋅k∣2(18)\begin{aligned} d\sigma(p\rightarrow p' + \gamma) &= d\sigma(p\rightarrow p')\cdot \int \frac{d^3k}{(2\pi)^3}\frac{1}{2k}\sum_{\lambda=1,2} e^2|\frac{p'\cdot \epsilon^{(\lambda)}}{p'\cdot k}-\frac{p\cdot \epsilon^{(\lambda)}}{p\cdot k}|^2\\ \end{aligned}\tag{18}

得到，辐射单光子的几率为：

d(prob)=d3k(2π)3∑λ=1,2e22k∣p′⋅ϵ(λ)p′⋅k−p⋅ϵ(λ)p⋅k∣2d(prob) = \frac{d^3k}{(2\pi)^3}\sum_{\lambda=1,2} \frac{e^2}{2k}|\frac{p'\cdot \epsilon^{(\lambda)}}{p'\cdot k}-\frac{p\cdot \epsilon^{(\lambda)}}{p\cdot k}|^2

对其在动量空间中的积分是发散的，这是因为上式子只在 soft-photon 下成立。为此，我们需要引入一个截断，综上得到辐射单光子的概率为：

απ∫0∣q∣dk1kI(v,v′)\frac{\alpha}{\pi}\int_{0}^{|\bm{q}|}dk \frac{1}{k}\mathcal{I}(\bm{v},\bm{v}')

若光子引入一个很小的质量 μ\mu，那么 (18)(18) 式可以写为：

dσ(p→p′+γ)=dσ(p→p′)⋅α2πlog⁡(−q2μ2)I(v,v′)≈−q2→∞dσ(p→p′)⋅απlog⁡(−q2μ2)log⁡(−q2m2)(19)\begin{aligned} d\sigma(p\rightarrow p' + \gamma) &= d\sigma(p\rightarrow p')\cdot \frac{\alpha}{2\pi} \log(-\frac{q^2}{\mu^2}) \mathcal{I}(\bm{v},\bm{v}')\\ &\overset{-q^2\rightarrow\infty}{\approx}d\sigma(p\rightarrow p')\cdot \frac{\alpha}{\pi} \log(-\frac{q^2}{\mu^2}) \log (-\frac{q^2}{m^2}) \end{aligned} \tag{19}