量子力学笔记（六）：自旋

自旋

Stern-Gerlach 实验

Stern-Gerlach 实验是德国物理学家奥托·施特恩和瓦尔特·格拉赫为证实原子角动量量子化于1921年到1922年期间完成的一个著名实验 $^{[3]}$。在该实验中，银原子射线束通过一个不均匀的磁场区域，射线束在磁场作用下发生偏折，最后落在屏上。如果原子磁矩的方向是可以任意取向的，则屏上形成一片黑斑。而实验发现屏上形成了几条清晰的黑斑，表明银原子的磁矩只能取几个特定的方向，从而验证了原子角动量的投影是量子化的。

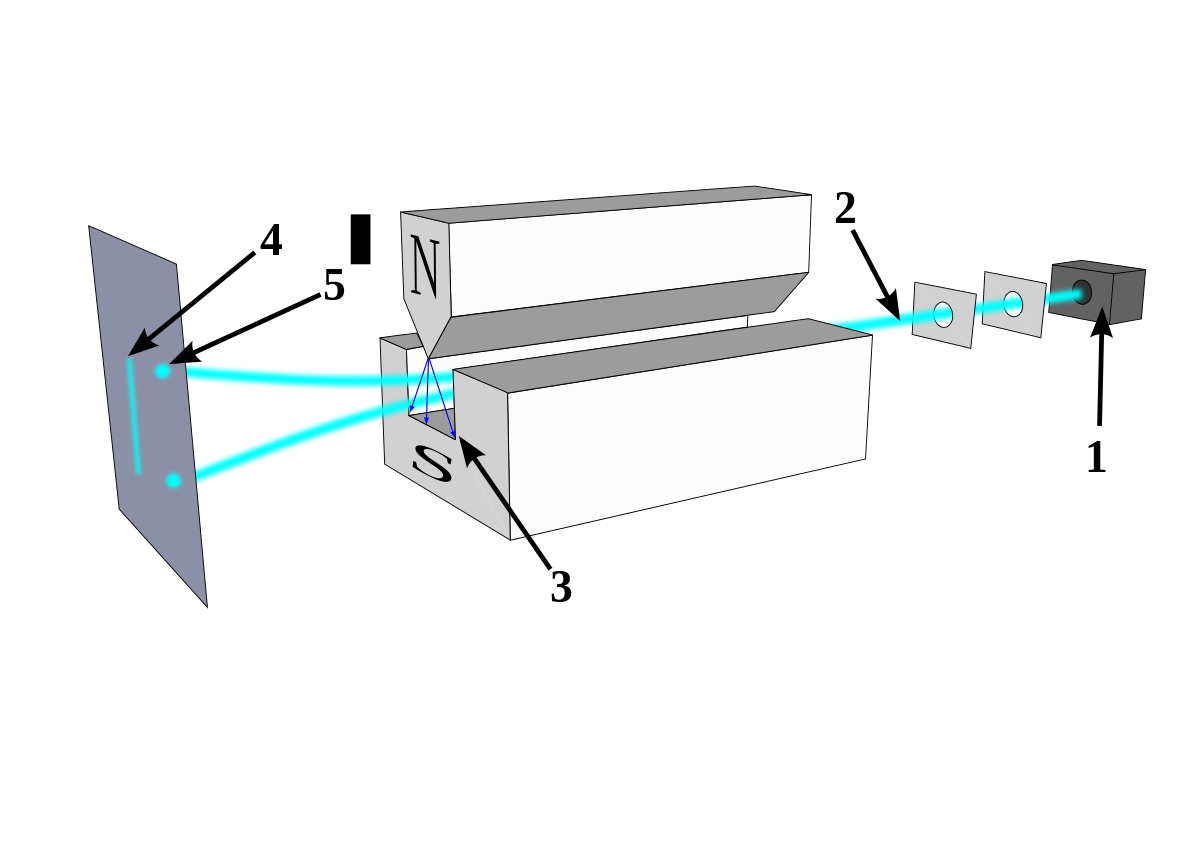
Fig：Stern-Gerlach 实验$^{[4]}$

在该实验中，发现了一些无法解释的现象：对于锂、钠、钾、金、银、铜等原子，实验得到了两条斑纹，反推得到原子的角动量应当是 $\frac{1}{2}$，按照当时的理论，角量子数只能取整数。

为了解释这一点，我们必须引入 自旋 的概念，自旋对应有 自旋角动量。自旋角动量可以取整数值或半整数值。对于电子来说，自旋角动量 $\hat{S}_z$ 为 $\pm\frac{1}{2}\hbar$

注意区分自旋与自转的区别，自旋角动量并不意味着是粒子自转产生的角动量，粒子自旋并无经典的对应物，自旋角动量应当理解为粒子的内禀角动量。后来我们会说明：相对论量子力学的狄拉克方程表明电子自旋蕴藏在波函数的旋量结构中。

自旋的描述

对于有自旋的粒子，用波函数描述其状态时。其不但要确定该粒子处于不同空间位置的几率，而且也要确定其自旋具有各种可能取向的几率。如此，波函数不仅依赖于三个连续变量——坐标 $x,y,z$，而且依赖于一个离散的 自旋变量 $\sigma$ $^{[5]}$。

下式给出了粒子处于 $dV$ 体积内，自旋为 $\sigma$ 的概率。

$\int |\psi(x,y,z;\sigma)|^2 dV \tag{1}$

在推导角动量算子的表达式时，我们从空间旋转群出发，从无限小旋转操作导出了角动量算子的代数结构。我们称自旋也为角动量，这是因为自旋算子也满足同角动量算子一样的代数结构：

$[\hat{S}_\alpha,\hat{S}_\beta] = i\hbar \varepsilon_{\alpha\beta\gamma} \hat{S}_{\gamma} \tag{2}$

类比角动量算子，也有如下对易关系：

$[\hat{S}^2,\hat{S}_{\alpha}] = 0 \tag{3}$

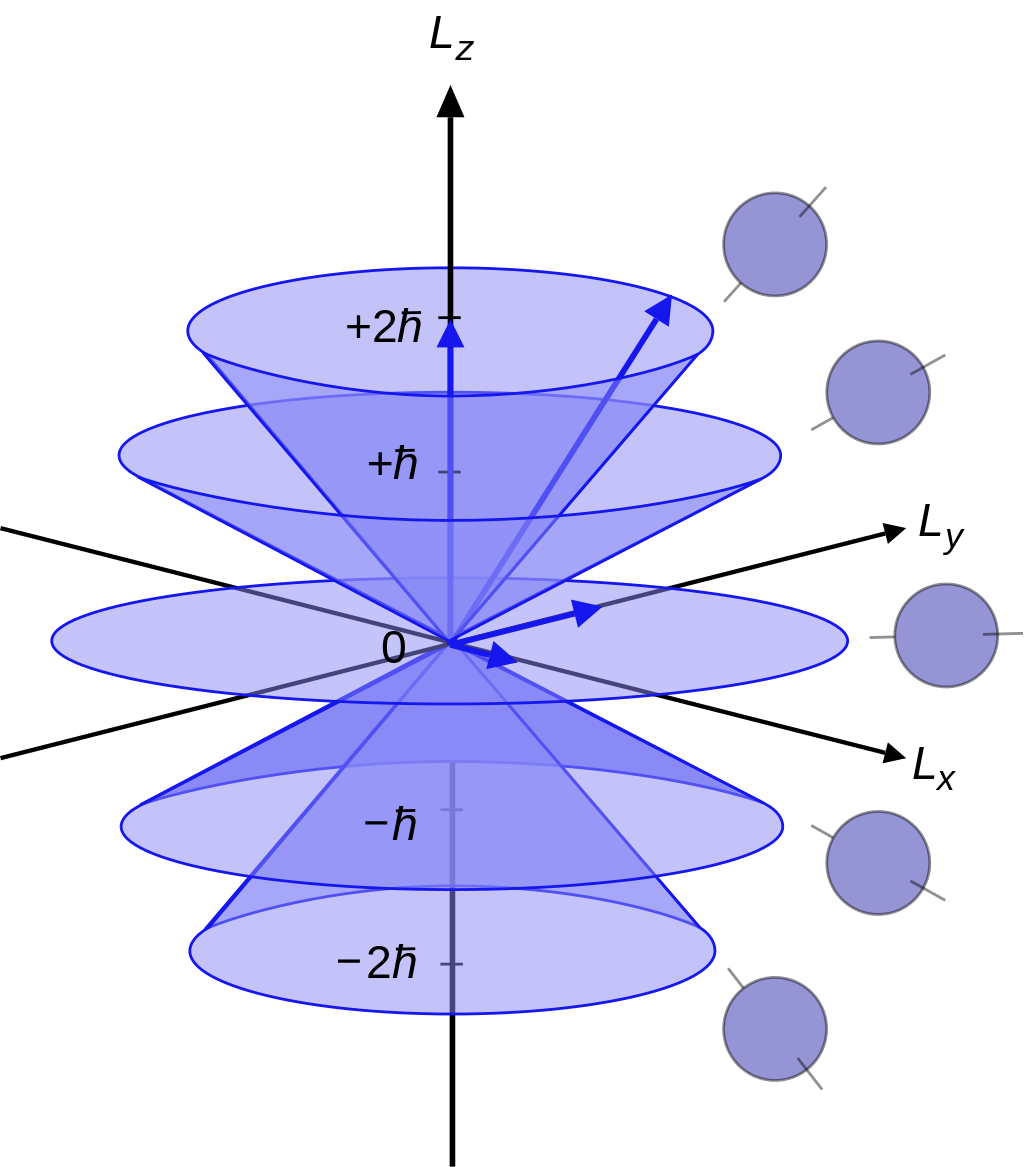
这说明，自旋的三个分量是不能够同时确定的，而 $\hat{S}^2$ 与 $\hat{S}_{\alpha}$ 是能够同时确定的，它们有共同本征态。以自旋为 $s$ 的粒子来说，$\hat{S}^2$ 的本征值为 $s(s+1)\hbar^2$，$\hat{S}_z$ 的本征值为 $-s,-s+1,\cdot,s-1,s$，$s$ 为整数或半整数。（回忆关于角动量分量本征值的表述，那里本征值只能取整数）。对应的自旋为 $s$ 的粒子，共有 $2s+1$ 个本征态。

对于电子来说，$s = \frac{1}{2}$，对应有自旋向上和自旋向下两种状态，我们记为 $|\uparrow\rangle,|\downarrow\rangle$。
对于光子来说，$s = 1$，按理说 $s_z = -1,0,1$，但考虑到光子是横向极化的，并无 $s = 0$ 的态，于是只有两种状态。

每个粒子的角动量应当是轨道角动量与自旋角动量的和：

$\bm{J} = \bm{L} + \bm{S}$

现在我们专门讨论波函数同自旋变量的关系。

考虑一个线性算子 $\hat{f}$ 作用到波函数 $\psi(\sigma)$ 上，得到：

$(\hat{f}\psi)(\sigma) = \sum_{\sigma'} f_{\sigma\sigma'} \psi(\sigma')\tag{4}$

这表明，作用于 $\sigma$ 上的算子可以表成一个 $(2s+1)$ 维的方阵。考虑自旋算子本身的作用：

$(\hat{S}\psi)(\sigma) = \sum_{\sigma'}S_{\sigma\sigma'}\psi(\sigma')$

考虑角动量算子的矩阵表示，类似的，自旋算子在 $\{\hat{S}^2,\hat{S}_z\}$ 本征态为基底构成的表象中的矩阵元为：

$\begin{aligned} &(\hat{S}_x) _{\sigma,\sigma - 1} = (\hat{S}_x) _{\sigma - 1,\sigma} = \frac{1}{2}\sqrt{(s+\sigma)(s-\sigma + 1)}\\ &(\hat{S}_y) _{\sigma,\sigma - 1} = -(\hat{S}_y) _{\sigma - 1,\sigma} = -\frac{1}{2}i\sqrt{(s+\sigma)(s-\sigma + 1)}\\ &(\hat{S}_z) _{\sigma,\sigma} = \sigma\\ \end{aligned}\tag{5}$

下面，我们重点对 $\frac{1}{2}$ 自旋的粒子进行讨论。

$\frac{1}{2}$ 自旋态

对于自旋 $\frac{1}{2}$ 的粒子，考虑 $(5)$ 式，这些矩阵的维数为 $2$。具有形式：

$\hat{\bm{S}} = \frac{1}{2}\hat{\bm{\sigma}} \tag{6}$

其中 $\hat{\bm{\sigma}}$ 为 泡利矩阵。有：

$\begin{aligned} &\hat{\sigma}_x = \begin{pmatrix} 0 & 1\\ 1 & 0\\ \end{pmatrix}\\ &\hat{\sigma}_y = \begin{pmatrix} 0 & -i\\ i & 0\\ \end{pmatrix}\\ &\hat{\sigma}_z = \begin{pmatrix} 1 & 0\\ 0 & -1\\ \end{pmatrix}\\ \end{aligned}\tag{7}$

泡利矩阵具有如下性质：

• $\hat{\sigma}_x^2 = \hat{\sigma}_y^2 = \hat{\sigma}_z^2 =1$
• $\hat{\sigma}_y\hat{\sigma}_z = i\hat{\sigma}_x,\hat{\sigma}_z\hat{\sigma}_x = i\hat{\sigma}_y,\hat{\sigma}_x\hat{\sigma}_y = i\hat{\sigma}_z$

由此得到有关泡利矩阵的对易关系与反对易关系：

$\begin{aligned} & [\hat{\sigma}_\alpha,\hat{\sigma}_\beta] = 2i\varepsilon_{\alpha\beta\gamma}\hat{\sigma}_{\gamma}\\ & \{\hat{\sigma}_\alpha,\hat{\sigma}_\beta\} = 2 \delta_{\alpha\beta}\\ \end{aligned}\tag{8}$

考虑自旋后（$s = \frac{1}{2}$），波函数可以用一个二分量表示，称为一个 旋量：

$\psi = \begin{pmatrix} \psi^1\\ \psi^2\\ \end{pmatrix} = \begin{pmatrix} \psi(\frac{1}{2})\\ \psi(-\frac{1}{2})\\ \end{pmatrix}$

有关旋量，在量子场论中会进一步说明。

现在考虑泡利矩阵的本征矢量与本征值：

$\begin{aligned} \sigma_x \quad 1:&\frac{1}{\sqrt{2}}\begin{pmatrix} 1 \\ 1\end{pmatrix}\\ -1:&\frac{1}{\sqrt{2}}\begin{pmatrix} 1 \\ -1\end{pmatrix}\\ \sigma_y \quad 1:&\frac{1}{\sqrt{2}}\begin{pmatrix} 1 \\ i\end{pmatrix}\\ -1:&\frac{1}{\sqrt{2}}\begin{pmatrix} 1 \\ -i\end{pmatrix}\\ \sigma_z \quad 1:&\begin{pmatrix} 1 \\ 0\end{pmatrix}\\ -1:& \begin{pmatrix} 0 \\ 1\end{pmatrix}\\ \end{aligned}$

一个自旋态 $|\delta\rangle$ 的 极化矢量 $\bm{p}_{\delta}$ 定义为：

$\bm{p}_{\delta} = \langle \delta |\bm{\sigma}|\delta\rangle \tag{9}$

经过态平均，这里 $\bm{p}_{\delta}$ 成为一个经典矢量。

一个自旋态 $|\lambda\rangle$ 的投影算子 $\hat{\pi}_{\lambda}$ 为：

$\hat{\pi}_{\lambda} = |\lambda\rangle\langle\lambda|$

如此定义的投影算子可以使用极化矢量表示为：

$\hat{\pi}_{\lambda} = \frac{1}{2}(1 + \bm{p}_{\lambda}\cdot\bm{\sigma}) \tag{10}$

例：在 $|\alpha\rangle = \begin{pmatrix} 1 \\ 0\end{pmatrix}$ 态中，测得自旋在 $\hat{\bm{n}}(\theta,\varphi)$ 方向的几率为：

$\begin{aligned} p_{n\alpha} &= \langle \alpha|\pi_{n}|\alpha\rangle\\ &= \langle \alpha | \frac{1}{2}(1 + \bm{n}\cdot\hat{\bm{\sigma}})|\alpha\rangle\\ &= \frac{1}{2} + \frac{1}{2}\begin{pmatrix} 1 & 0\end{pmatrix} \begin{pmatrix} n_z & n_x-in_y \\ n_x+in_y & -n_z \end{pmatrix} \begin{pmatrix} 1 \\ 0 \end{pmatrix}\\ & = \frac{1}{2}(1+n_z) = \frac{1}{2}(1+\cos\theta) \end{aligned}$

角动量相加

现在考虑角动量 $\bm{j}_1$ 与 $\bm{j}_2$ 相加的情形。
角动量具有如下对易关系：

$\begin{aligned} \hat{\bm{j}}_1 \times \hat{\bm{j}}_1 = i\hbar \hat{\bm{j}}_1 \\ \hat{\bm{j}}_2 \times \hat{\bm{j}}_2 = i\hbar \hat{\bm{j}}_2 \\ \end{aligned}\tag{11}$

总角动量 $\bm{J} = \bm{j}_1 + \bm{j}_2$

得到：

$\begin{aligned} \hat{\bm{J}} \times \hat{\bm{J}} &= (\hat{\bm{j}}_1 + \hat{\bm{j}}_2)\times(\hat{\bm{j}}_1 + \hat{\bm{j}}_2)\\ &= \hat{\bm{j}}_1 \times \hat{\bm{j}}_1 + \hat{\bm{j}}_2 \times \hat{\bm{j}}_2\\ &= i\hbar \hat{\bm{j}}_1 + i\hbar \hat{\bm{j}}_2\\ &= i\hbar\hat{\bm{J}}\\ \end{aligned}\tag{12}$

如此，角动量的相加也得到角动量。

考虑 $(\hat{J}^2,\hat{J}_z)$ 的共同本征态 $|Jm\rangle$，有下列本征值方程：

$\begin{aligned} & \hat{J}^2 |Jm\rangle = J(J+1)\hbar^2|Jm\rangle \\ & \hat{J}_z |Jm\rangle = m\hbar |Jm\rangle \\ \end{aligned}\tag{13}$

$m$ 共有 $2J+1$ 个不同的取值。

要完全确定这个系统的状态。可以使用如下两组基底：

• $(\hat{j}_1^2,\hat{j}_2^2,\hat{j}_{1z},\hat{j}_{2z})$ 的共同本征态 $|j_1j_2m_1m_2\rangle$。
• $(\hat{j}_1^2,\hat{j}_2^2,\hat{J}^2,\hat{J}_{z})$ 的共同本征态 $|j_1j_2Jm\rangle$。

其中第一组基底是非耦合的：

$|j_1j_2m_1m_2\rangle = |j_1m_1\rangle|j_2m_2\rangle$

这实际上就是用 $(\hat{j}_1^2,\hat{j}_{1z})$ 与 $(\hat{j}_2^2,\hat{j}_{2z})$ 各自的本征态构成的直积态作为基底。

第二组基底是 耦合 的。

联系起这两组基底的系数称为 Clebsch–Gordan 系数，具体来说有：

$|j_1j_2Jm\rangle = \sum_{m_1m_2}C_{j_1m_1j_2m_2}^{Jm} |j_1j_2m_1m_2\rangle \tag{14}$

一般来说，$\bm{j}_1,\bm{j}_2$ 相加得到 $\bm{J}$ 的量子数 $J$ 可能取值为：

$J = j_1+j_2,j_1+j_2-1,j_1+j_2-2,\cdots,|j_1-j_2|$

两电子自旋态

现在考虑两个电子的自旋可能处于的状态。

$(\hat{S}^2_1,\hat{S}_{1z})$ 的本征态 $|S_1m_1\rangle$ 记为 $\xi_{\pm}$，$(\hat{S}^2_2,\hat{S}_{2z})$ 的本征态 $|S_2m_2\rangle$ 记为 $\eta_{\pm}$。

于是 $\{\xi_{+}\eta_{+},\xi_{+}\eta_{-},\xi_{-}\eta_{+},\xi_{-}\eta_{-}\}$ 成为一组非耦合基。

考虑总自旋：

$\hat{\bm{S}} = \hat{\bm{S}}_1 + \hat{\bm{S}}_2$

对应的，$\hat{S}^2$ 算子在非耦合基下的矩阵表示为：

$\hat{S}^2 = \hbar^2\begin{pmatrix} 2 & 0 & 0 & 0\\ 0 & 1 & 1 & 0\\ 0 & 1 & 1 & 0\\ 0 & 0 & 0 & 2\\ \end{pmatrix}\tag{15}$

此处举一个例子进行计算：

$\begin{aligned} \langle \xi_{+}\eta_{-}|\hat{S}^2|\xi_{-}\eta_{+}\rangle &= \langle \xi_{+}\eta_{-}|2\hat{S}_{1x}\hat{S}_{2x} + 2\hat{S}_{1y}\hat{S}_{2y}|\xi_{-}\eta_{+}\rangle\\ &= \frac{\hbar^2}{2} \langle \xi_{+}\eta_{-}| \sigma_{1x}\sigma_{2x} + \sigma_{1y}\sigma_{2y} |\xi_{-}\eta_{+}\rangle\\ & = \hbar^2\\ \end{aligned}$

对应的，得到 $\hat{S}^2$ 的本征态：

$\begin{aligned} &S = 1:\quad \xi_{+}\eta_{+},\quad \xi_{-}\eta_{-},\quad \frac{1}{\sqrt{2}}(\xi_{+}\eta_{-}+\xi_{-}\eta_{+})\\ &S = 0: \quad \frac{1}{\sqrt{2}}(\xi_+\eta_{-}-\xi_-\eta_{+}) \end{aligned}\tag{16}$

不难看出，它们同时也是 $\hat{S}_z$ 的本征态。如此，得到 $4$ 个耦合基。

$\chi_{S,m_S} = \chi_{1,1},\chi_{1,0},\chi_{1,-1},\chi_{0,0}$

考虑对称性。其中交换反对称的解为 自旋单态 Singlet

$\chi_{0,0} = \frac{1}{\sqrt{2}}(\xi_{+}\eta_{-}-\xi_{-}\eta_{+})\tag{17}$

对称的解为 自旋三重态 Triplet

$\left\{ \begin{aligned} \chi_{1,1} &= \xi_{+}\eta_{+}\\ \chi_{1,0} &= \frac{1}{\sqrt{2}}(\xi_{+}\eta_{-}+\xi_{-}\eta_{+})\\ \chi_{1,-1} &= \xi_{-}\eta_{-}\\ \end{aligned} \right.\tag{18}$

轨道-自旋耦合

考虑自旋角动量与轨道角动量相加的情形：

$\bm{J} = \bm{L} + \bm{S}$

如此非耦合基为 ：$|lmm_S\rangle = Y_{lm}\xi_{\pm}$。
耦合基为 $|ljm_j\rangle = \chi_{jm_j}$

其中 $j = l\pm\frac{1}{2}$，得到 $m_j = \pm j,\pm (j-1),\pm (j-2),\pm \frac{3}{2},\pm\frac{1}{2}$。

考虑到：

$\begin{aligned} J^2 &= (L+S)^2\\ &= L^2 + S^2 + 2L\cdot S\\ &\Rightarrow L\cdot S = \frac{1}{2}(J^2 - L^2 - S^2)\\ \end{aligned}$

我们可以得到以下的对易关系：

$[L\cdot S,L^2] = [L\cdot S,S^2] = [L\cdot S,J^2] = [L\cdot S,J_z] = 0$

如此，我们发现：若哈密顿量中有 $L\cdot S$，在耦合基中是能够将哈密顿量对角化的，在非耦合基中这是做不到的。下面举一例。

自旋-轨道耦合作用与碱金属原子光谱的双线结构

原子中的电子绕原子核作空间运动时将产生磁场，这个磁场必定与电子固有磁矩发生作用，使原有能极劈裂并产生附加能移。这就是自旋—轨道耦合作用$^{[1]}$。

设电子的轨道运动在电子所处位置产生的磁场为 $\bm{H}$。那么其应当等效为以电子为参考系，原子核绕电子回旋产生的磁场，按照毕奥-萨法尔定律得到：

$\bm{H} = -\frac{1}{c}\bm{v}\times \frac{Z_e\bm{r}}{r^3} = \frac{1}{c}\bm{E}\times\bm{v} \tag{19}$

电子的磁矩为：

$\bm{\mu} = -\frac{e\hbar}{2mc}\bm{\sigma}$

可以得到磁矩在磁场中的能量为：

$\begin{aligned} -\bm{\mu}\cdot\bm{H} &= \frac{e\hbar}{2mc}\bm{\sigma} \cdot (\frac{1}{c}\bm{E}\times\bm{v})\\ &= \frac{1}{m^2c^2 r}\frac{dV}{dr}\bm{L}\cdot\bm{S}\\ \end{aligned}$

上式相比正确的表达式，缺少了 $\frac{1}{2}$ 这个因子。这项称为 托马斯进动修正（正确考虑洛伦兹变换）。于是，得到正确的轨道-自旋耦合项为：

$\frac{1}{2mc^2r}\frac{dV}{dr}\bm{L}\cdot\bm{S}$

这项修正的量级为 $\beta^2$，为相对论性修正。

碱金属原子光谱双线结构（如钠黄光）的物理根源正在于，最外层价电子自旋与轨道角动量之间平行反平行耦合使能级出现双重劈裂。此时哈密顿量为：

$H = -\frac{\hbar^2}{2m}\nabla^2 + V(r) + \xi(r) \bm{L}\cdot\bm{S}$

其中 $\xi(r) = \frac{\hbar^2}{2m^2c^2} \frac{1}{r}\frac{dV}{dr}$

由此可得轨道-自旋耦合项造成的能移为：

$\Delta E = \frac{1}{2}\xi_{nl}[j(j+1) - l(l+1) - \frac{3}{4} ]$

其中：

$\xi_{nl} = \int_{0}^{\infty}[R_{nl}(r)]^2 \xi(r)r^2dr$

可以得到对于自旋-轨道角动量平行耦合与反平行耦合的态，能量变化为：

$\left\{ \begin{aligned} &\Delta E = \frac{l}{2}\xi_{nl}\quad &j = l+\frac{1}{2}\\ &\Delta E = -\frac{l+1}{2}\xi_{nl}\quad &j = l-\frac{1}{2}\\ \end{aligned} \right.$

耦合基在非耦合基下的展开

考虑到耦合基 $\chi_{l+\frac{1}{2},m+\frac{1}{2}}$ 可以使用非耦合基展开为如下形式：

$\chi_{l+\frac{1}{2},m+\frac{1}{2}} = \alpha_1Y_{lm}\xi_+ + \alpha_2Y_{lm+1}\xi_-$

归一化条件给出 $|\alpha_1|^2+|\alpha_2|^2=1$，现在我们设法确定 $\alpha_1$ 与 $\alpha_2$ 的比值，就可以给出 $\alpha_1$，$\alpha_2$。为达到此目的，我们考虑 $\hat{J}^2$ 的作用：

一方面：$\chi_{l+\frac{1}{2},m+\frac{1}{2}}$ 作为 $\hat{J}^2$ 的本征态，有

$\hat{J}^2\chi_{l+\frac{1}{2},m+\frac{1}{2}} = (l+\frac{1}{2})(l+\frac{3}{2})\hbar^2 \chi_{l+\frac{1}{2},m+\frac{1}{2}} \tag{20}$

另一方面：

$\begin{aligned} \hat{J}^2 &= (\hat{L}+\hat{S})^2\\ &= \hat{L}^2 + \hat{S}^2 + 2\hat{L}\cdot\hat{S}\\ &= \hat{L}^2 + \hat{S}^2 + 2\hat{L}_z\hat{S}_z + \hat{L}_+\hat{S}_{-} + \hat{L}_-\hat{S}_{+}\\ \end{aligned}$

考虑到：

$\begin{aligned} 2\hat{L}\cdot\hat{S}(Y_{lm}\xi_+) &= (2\hat{L}_z\hat{S}_z + \hat{L}_+\hat{S}_{-} + \hat{L}_-\hat{S}_{+})(Y_{lm}\xi_+)\\ &= m\hbar^2 Y_{lm}\xi_+ + \sqrt{l(l+1)-m(m+1)})\hbar^2 Y_{lm+1}\xi_-\\ 2\hat{L}\cdot\hat{S}(Y_{lm+1}\xi_-) &= (2\hat{L}_z\hat{S}_z + \hat{L}_+\hat{S}_{-} + \hat{L}_-\hat{S}_{+})(Y_{lm+1}\xi_-)\\ &= -(m+1)\hbar^2 Y_{lm+1}\xi_- + \sqrt{l(l+1)-m(m+1)}\hbar^2 Y_{lm}\xi_+\\ \end{aligned}$

于是得到：

$\begin{aligned} \hat{J}^2\chi_{l+\frac{1}{2},m+\frac{1}{2}} =& [\alpha_1(l(l+1)+\frac{3}{4} + m) + \alpha_2\sqrt{l(l+1)-m(m+1)}]\hbar^2Y_{lm}\xi_+\\ &+[\alpha_2(l(l+1)+\frac{3}{4} - (m+1)) + \alpha_1\sqrt{l(l+1)-m(m+1)}]\hbar^2Y_{lm+1}\xi_-\\ \end{aligned}$

考虑到 $(20)$ 式子，应当有 $Y_{lm}\xi_+$ 与 $Y_{lm+1}\xi_-$ 前的系数分别相等。如此，得到化简之后的式子为：

$\left\{ \begin{aligned} & \alpha_2\sqrt{l(l+1)-m(m+1)} = \alpha_1(l-m)\\ & \alpha_1\sqrt{l(l+1)-m(m+1)} = \alpha_2(l+m+1)\\ \end{aligned} \right.$

可得：

$\frac{\alpha_1}{\alpha_2} = \sqrt{\frac{l+m+1}{l-m}}$

考虑归一化条件，得到：

$\begin{aligned} &\alpha_1 = \sqrt{\frac{l+m+1}{2l+1}}\\ &\alpha_2 = \sqrt{\frac{l-m}{2l+1}}\\ \end{aligned}$

同时，我们也可以得到 $\chi_{l-\frac{1}{2},m+\frac{1}{2}}$ 的表达式，合写为：

$\begin{aligned} \chi_{l+\frac{1}{2},m+\frac{1}{2}} &= \frac{1}{\sqrt{2l+1}}\begin{pmatrix} \sqrt{l+m+1} Y_{lm}\\ \sqrt{l-m} Y_{lm+1}\\ \end{pmatrix}\\ \chi_{l-\frac{1}{2},m+\frac{1}{2}} &= \frac{1}{\sqrt{2l+1}}\begin{pmatrix} \sqrt{l-m} Y_{lm}\\ -\sqrt{l+m+1} Y_{lm+1}\\ \end{pmatrix}\\ \end{aligned}\tag{21}$

参考资料

1. 张永德，量子力学讲义
2. 沈瑞，南京大学，量子力学课程讲义
3. 施特恩－格拉赫实验. (2019, February 23). Retrieved from 维基百科, 自由的百科全书: https://zh.wikipedia.org/w/index.php?title=施特恩－格拉赫实验&oldid=53312590
4. By Tatoute - Own work, CC BY-SA 4.0, https://commons.wikimedia.org/w/index.php?curid=34095239
5. 朗道，量子力学