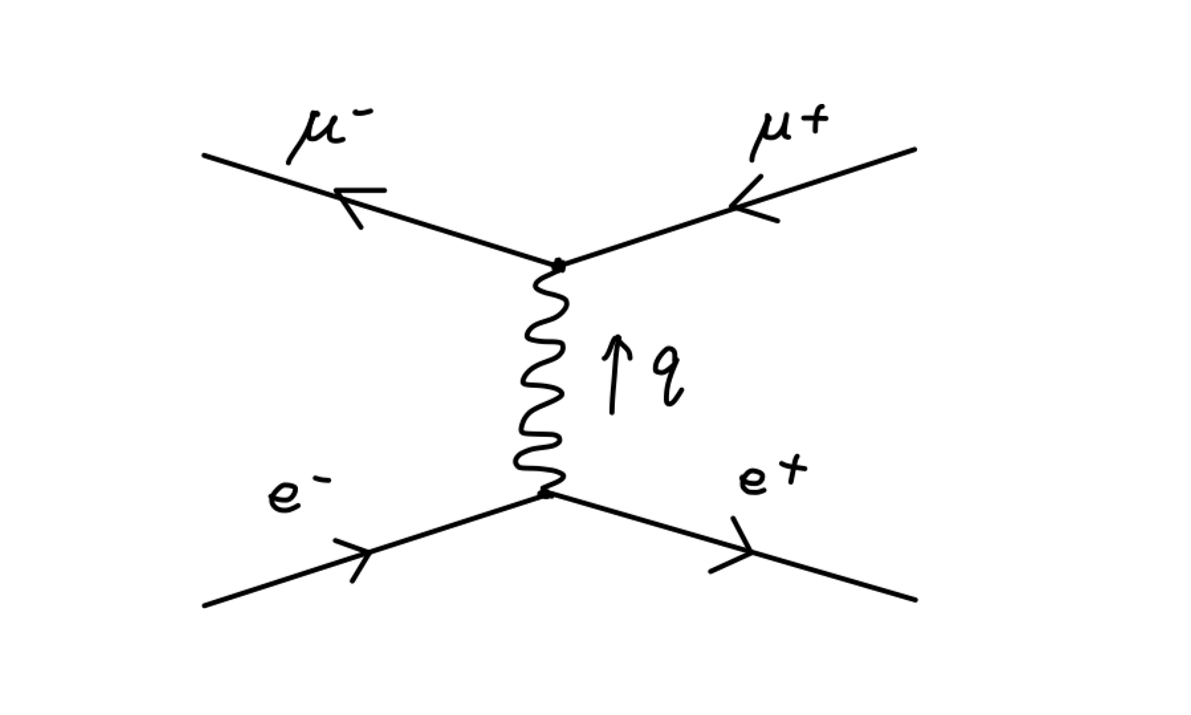
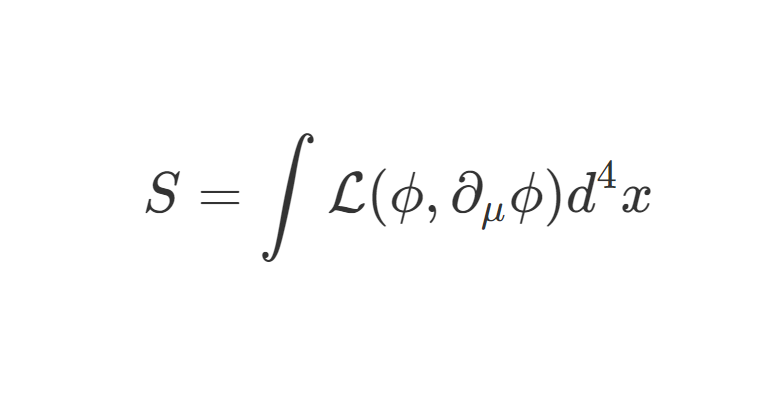Dirac 方程的自由粒子解

Dirac 方程为：

(i∂−m)ψ=0(1)(i\cancel{\partial}-m)\psi = 0 \tag{1}

其中自由粒子解是一系列平面波的叠加，对于四动量为 pp 的正频平面波来说，其波函数为：

ψ(x)=u(p)e−ip⋅x(2)\psi(x) = u(p)e^{-ip\cdot x} \tag{2}

此处特别说明，正频平面波对应的是正粒子解，p0>0p^0>0

代入 (1)(1) 得到：

(p−m)u(p)=0(3)(\cancel{p}-m)u(p) = 0 \tag{3}

我们先考虑四动量为 pμ=(m,0)p^{\mu} = (m,0) 的特殊情况，之后就可以通过 boost 得到一般形式的平面波解。此时 (3)(3) 成为：

(γ0m−m)u(p)=0(\gamma^0m - m)u(p) = 0

即：

(−111−1)u(p)=0\begin{pmatrix} -1 & 1\\ 1 & -1\\ \end{pmatrix}u(p) = 0

这里的 “1” 实际上指一个 2×22\times 2 的单位阵，我们以后就不特殊说明了。

得到 u(p)u(p) 的本征值大于零的解为：

u(p)=m(ξξ)(4)u(p) = \sqrt{m}\begin{pmatrix} \xi\\ \xi\\ \end{pmatrix} \tag{4}

上式中 ξ\xi 是一个具有两个分量的旋量；为了之后的方便，此处我们加上因子 m\sqrt{m}。这里我们舍去的本征值小于零的 “负能解”：

u(p)=m(ξ−ξ)u(p) = \sqrt{m}\begin{pmatrix} \xi\\ -\xi\\ \end{pmatrix}

对于 ξ\xi 来说，我们规定如下归一化条件：

ξ†ξ=1(5)\xi^\dagger\xi = 1 \tag{5}

此时：

u†(p)u(p)=2mξ†ξ=2m(6)u^\dagger(p)u(p) = 2m\xi^\dagger\xi = 2m \tag{6}

现在我们对上述解进行 boost，不失一般性的，我们可以选取 E,p3E,p^3 进行boost，其无穷小形式为：

(Ep3)=(1+η(0110))(m0)\begin{pmatrix} E\\ p^3\\ \end{pmatrix}=(1+\eta\begin{pmatrix} 0 & 1\\ 1 & 0\\ \end{pmatrix} )\begin{pmatrix} m\\ 0\\ \end{pmatrix}

有限变换为：

(Ep3)=exp⁡(η(0110))(m0)=(sinh⁡(η(0110))+cosh⁡(η(0110)))(m0)=(sinh⁡η(0110)+cosh⁡η(1001))(m0)=(mcosh⁡ηmsinh⁡η)\begin{aligned} \begin{pmatrix} E\\ p^3\\ \end{pmatrix}&=\exp(\eta\begin{pmatrix} 0 & 1\\ 1 & 0\\ \end{pmatrix} )\begin{pmatrix} m\\ 0\\ \end{pmatrix}\\ &=(\sinh(\eta\begin{pmatrix} 0 & 1\\ 1 & 0\\ \end{pmatrix})+\cosh(\eta\begin{pmatrix} 0 & 1\\ 1 & 0\\ \end{pmatrix}) )\begin{pmatrix} m\\ 0\\ \end{pmatrix}\\ &= (\sinh\eta\begin{pmatrix} 0 & 1\\ 1 & 0\\ \end{pmatrix}+\cosh\eta\begin{pmatrix} 1 & 0\\ 0 & 1\\ \end{pmatrix} )\begin{pmatrix} m\\ 0\\ \end{pmatrix}\\ &= \begin{pmatrix} m\cosh \eta\\ m\sinh \eta\\ \end{pmatrix}\\ \end{aligned}

上述推导中用到性质：

(0110)(0110)=(1001)\begin{pmatrix} 0 & 1\\ 1 & 0\\ \end{pmatrix}\begin{pmatrix} 0 & 1\\ 1 & 0\\ \end{pmatrix} = \begin{pmatrix} 1 & 0\\ 0 & 1\\ \end{pmatrix}

注意 sinh⁡A\sinh A 中只含有奇次项，而 cosh⁡A\cosh A 中只含有偶次项。

现在考虑对 u(p)u(p) 的boost，我们使用 S03S^{03} 作为生成元进行 boost：

u(p)=exp⁡(−12η(σ300−σ3))m(ξξ)=(cosh⁡(12η)(1001)−sin⁡(12η)(σ300−σ3))m(ξξ)=(eη2(1−σ32)+e−η2(1+σ32)00eη2(1+σ32)+e−η2(1−σ32))m(ξξ)\begin{aligned} u(p) &= \exp(-\frac{1}{2}\eta\begin{pmatrix} \sigma^3 & 0\\ 0 & -\sigma^3\\ \end{pmatrix} )\sqrt{m}\begin{pmatrix} \xi\\ \xi\\ \end{pmatrix}\\ &= (\cosh(\frac{1}{2}\eta)\begin{pmatrix} 1 & 0\\ 0 & 1\\ \end{pmatrix} - \sin(\frac{1}{2}\eta)\begin{pmatrix} \sigma^3 & 0\\ 0 & -\sigma^3\\ \end{pmatrix} )\sqrt{m}\begin{pmatrix} \xi\\ \xi\\ \end{pmatrix}\\ & = \begin{pmatrix} e^{\frac{\eta}{2}}(\frac{1-\sigma^3}{2}) + e^{-\frac{\eta}{2}}(\frac{1+\sigma^3}{2}) & 0\\ 0 & e^{\frac{\eta}{2}}(\frac{1+\sigma^3}{2}) + e^{-\frac{\eta}{2}}(\frac{1-\sigma^3}{2})\\ \end{pmatrix}\sqrt{m}\begin{pmatrix} \xi\\ \xi\\ \end{pmatrix}\\ \end{aligned}

利用：

meη2=meη=mcosh⁡η+msinh⁡η=E+p3me−η2=E−p3\begin{aligned} &\sqrt{m}e^{\frac{\eta}{2}} = \sqrt{me^{\eta}} = \sqrt{m\cosh\eta + m\sinh\eta} = \sqrt{E + p^3}\\ &\sqrt{m}e^{-\frac{\eta}{2}} = \sqrt{E - p^3}\\ \end{aligned}

得到：

u(p)=([E+p3(1−σ32)+E−p3(1+σ32)]ξ[E+p3(1+σ32)+E−p3(1−σ32)]ξ)(7)u(p) = \begin{pmatrix} [\sqrt{E+p^3}(\frac{1-\sigma^3}{2}) + \sqrt{E-p^3}(\frac{1+\sigma^3}{2})]\xi\\ [\sqrt{E+p^3}(\frac{1+\sigma^3}{2}) + \sqrt{E-p^3}(\frac{1-\sigma^3}{2})]\xi\\ \end{pmatrix}\tag{7}

考虑到：

[E+p3(1−σ32)+E−p3(1+σ32)]2=(E+p3)(1−σ32)2+(E−p3)(1+σ32)2+2(E+p3)(E−p3)(1−σ32)(1+σ32)=(E+p3)1−σ32+(E−p3)1+σ32=E−p3σ3\begin{aligned} &[\sqrt{E+p^3}(\frac{1-\sigma^3}{2}) + \sqrt{E-p^3}(\frac{1+\sigma^3}{2})]^2\\ =& (E+p^3)(\frac{1-\sigma^3}{2})^2 + (E-p^3)(\frac{1+\sigma^3}{2})^2 + 2\sqrt{(E+p^3)(E-p^3)}(\frac{1-\sigma^3}{2})(\frac{1+\sigma^3}{2})\\ =& (E+p^3)\frac{1-\sigma^3}{2} + (E-p^3)\frac{1+\sigma^3}{2}\\ =& E-p^3\sigma^3\\ \end{aligned}

我们定义：σμ=(1,σ),σˉμ=(1,−σ)\sigma^{\mu} = (1,\bm{\sigma}),\bar{\sigma}^{\mu} = (1,-\bm{\sigma})，可得：

[E+p3(1−σ32)+E−p3(1+σ32)]2=p⋅σ[E+p3(1+σ32)+E−p3(1−σ32)]2=p⋅σˉ\begin{aligned} [\sqrt{E+p^3}(\frac{1-\sigma^3}{2}) + \sqrt{E-p^3}(\frac{1+\sigma^3}{2})]^2 = p\cdot \sigma\\ [\sqrt{E+p^3}(\frac{1+\sigma^3}{2}) + \sqrt{E-p^3}(\frac{1-\sigma^3}{2})]^2 = p\cdot \bar{\sigma}\\ \end{aligned}

于是 (7)(7) 式可以写为：

u(p)=(p⋅σξp⋅σˉξ)u(p) = \begin{pmatrix} \sqrt{p \cdot \sigma} \xi\\ \sqrt{p \cdot \bar{\sigma}} \xi\\ \end{pmatrix}

在来看 u(p)u(p) 满足的归一化关系，我们期望它仍然遵从 (6)(6) 式的结果，那么这样 u(p)u(p) 所满足的归一化关系就是洛伦兹不变的。可是很可惜：

u†(p)u(p)=(p⋅σ+p⋅σˉ)=2Epu^\dagger(p)u(p) = (p\cdot \sigma + p\cdot \bar{\sigma}) = 2E_{\bm{p}}

显然不是洛伦兹不变的。因此，我们需要修改归一化条件，在上一篇中我们实际上也发现类似的事情：ψ†ψ\psi^\dagger\psi 并不洛伦兹不变的，而 ψˉψ\bar{\psi}\psi 是洛伦兹不变的。因此，我们考虑：

uˉ(p)=u(p)γ0=(p⋅σˉξ†p⋅σξ†)\bar{u}(p) = u(p)\gamma^0 = \begin{pmatrix} \sqrt{p\cdot\bar{\sigma}}\xi^\dagger\\ \sqrt{p\cdot\sigma}\xi^\dagger\\ \end{pmatrix}

有：

uˉ(p)u(p)=2(p⋅σ)(p⋅σˉ)=2E2−p2=2m\bar{u}(p)u(p) = 2\sqrt{(p\cdot \sigma)(p\cdot \bar{\sigma})} = 2\sqrt{E^2 - \bm{p}^2} = 2m

这件事情很棒。

我们现在想问：ξ\xi 的取值如何？

不妨继续考虑对 p3p^3 进行 boost 的情形。考虑到 σ3\sigma^3 的本征值与对应本征态为：

+1(10)−1(01)+1 \quad \begin{pmatrix} 1\\ 0\\ \end{pmatrix}\quad -1 \quad \begin{pmatrix} 0\\ 1\\ \end{pmatrix}

任意一个 ξ\xi 都可以写为这两个本征态的线性组合。我们考虑 ξ\xi 为其本征态的情况：

{u1(p)=(E−p3σ3(10)E+p3σ3(10))=(E−p3(10)E+p3(10))⟶large boost2E(0010)u2(p)=(E−p3σ3(01)E+p3σ3(01))=(E+p3(01)E−p3(01))⟶large boost2E(0100)\left\{ \begin{aligned} u_1(p) &= \begin{pmatrix} \sqrt{E-p^3\sigma^3} \begin{pmatrix} 1\\ 0\\ \end{pmatrix}\\ \sqrt{E+p^3\sigma^3} \begin{pmatrix} 1\\ 0\\ \end{pmatrix} \end{pmatrix} = \begin{pmatrix} \sqrt{E-p^3} \begin{pmatrix} 1\\ 0\\ \end{pmatrix}\\ \sqrt{E+p^3} \begin{pmatrix} 1\\ 0\\ \end{pmatrix} \end{pmatrix} \overset{large\ boost}{\longrightarrow} \sqrt{2E}\begin{pmatrix} 0\\ 0\\ 1\\ 0\\ \end{pmatrix}\\ u_2(p) &= \begin{pmatrix} \sqrt{E-p^3\sigma^3} \begin{pmatrix} 0\\ 1\\ \end{pmatrix}\\ \sqrt{E+p^3\sigma^3} \begin{pmatrix} 0\\ 1\\ \end{pmatrix} \end{pmatrix} = \begin{pmatrix} \sqrt{E+p^3} \begin{pmatrix} 0\\ 1\\ \end{pmatrix}\\ \sqrt{E-p^3} \begin{pmatrix} 0\\ 1\\ \end{pmatrix} \end{pmatrix} \overset{large\ boost}{\longrightarrow} \sqrt{2E}\begin{pmatrix} 0\\ 1\\ 0\\ 0\\ \end{pmatrix}\\ \end{aligned} \right.

large boost：E≫mE \gg m

我们之后将提到这两个解正是 螺旋度算子 helicity operator 的两个本征态。螺旋度算子定义为：

h^≡p^⋅S=12p^(σ00−σ)\hat{h} \equiv \hat{\bm{p}}\cdot\bm{S} = \frac{1}{2}\hat{\bm{p}} \begin{pmatrix} \bm{\sigma} & 0\\ 0 & -\bm{\sigma}\\ \end{pmatrix}

注意上式中 p^\hat{\bm{p}} 并非指动量算子，而是与动量同向的单位向量。

在仅对 p3p^3 进行 boost 的情形，螺旋度算子成为：

h^=12(σ300−σ3)\hat{h} = \frac{1}{2}\begin{pmatrix} \sigma^3 & 0\\ 0 & -\sigma^3\\ \end{pmatrix}

可得：u1(p),u2(p)u_1(p),u_2(p) 分别为螺旋度 h=+12,h=−12h = +\frac{1}{2},h = -\frac{1}{2} 的本征态。其中 h=+12h = +\frac{1}{2} 的粒子称为 右手的 right-handed，对应 s=1s=1；h=−12h = -\frac{1}{2} 的粒子称为 左手的 right-handed，对应 s=2s=2。

现在我们作总结，我们找的是如下形式的正粒子解：

ψ(x)=u(p)e−ip⋅x,p2=m2,p0>0us(p)=(p⋅σξsp⋅σˉξs),s=1,2\begin{aligned} &\psi(x) = u(p)e^{-ip\cdot x},\quad p^2=m^2,\quad p^0>0\\ &u^s(p) = \begin{pmatrix} \sqrt{p\cdot\sigma} \xi^s\\ \sqrt{p\cdot\bar{\sigma}} \xi^s\\ \end{pmatrix},\quad s=1,2\\ \end{aligned}

满足：

uˉr(p)us(p)=2mδrs(8)\bar{u}^r(p)u^s(p) = 2m\delta^{rs} \tag{8}

现在考虑负频解：

ψ(x)=v(p)eip⋅x,p2=m2,p0>0(9)\psi(x) = v(p)e^{ip\cdot x},\quad p^2=m^2,\quad p^0>0\tag{9}

这对应反粒子解，实际上是将正频情形中的负能解修改得到的：我们为了得到一个正能量的解，我们改变了指数项的符号。

代入 Dirac 方程得到：

(−p−m)v(p)=0(10)(-\cancel{p}-m)v(p) = 0 \tag{10}

那么静止粒子解成为：

v(p)=m(ηs−ηs)(11)v(p) = \sqrt{m}\begin{pmatrix} \eta^s\\ -\eta^s\\ \end{pmatrix}\tag{11}

其中 ηs,s=1,2\eta^s,s=1,2 是两分量旋量的另一组基底。满足：

η†η=1(12)\eta^\dagger\eta = 1 \tag{12}

类似的，我们考虑对 p3p^3 进行 boost 得到一般的运动粒子解。

v(p)=m(p⋅σηs−p⋅σˉηs)(13)v(p) = \sqrt{m}\begin{pmatrix} \sqrt{p\cdot \sigma}\eta^s\\ -\sqrt{p\cdot \bar{\sigma}}\eta^s\\ \end{pmatrix}\tag{13}

满足：

vˉr(p)vs(p)=−2mδrs(14)\bar{v}^r(p)v^s(p) = -2m\delta^{rs} \tag{14}

反粒子与正粒子的四个正能解就构成了 Dirac 方程自由粒子解的一组正交基。满足：

uˉr(p)vs(p)=0(15)\bar{u}^r(p) v^s(p) = 0 \tag{15}

在之后的计算中，我们常常包含了对自旋态的求和。因此以下式子在计算中很重要：

∑sus(p)uˉs(p)=∑s(p⋅σξsp⋅σˉξs)(p⋅σˉξs†p⋅σξs†)=∑sξsξs†(p⋅σp⋅σˉp⋅σp⋅σp⋅σˉp⋅σˉp⋅σˉp⋅σ)=(mp⋅σp⋅σˉm)=γ⋅p+m(16)\begin{aligned} \sum_{s}u^s(p)\bar{u}^s(p) &= \sum_s \begin{pmatrix} \sqrt{p\cdot \sigma} \xi^{s}\\ \sqrt{p\cdot \bar{\sigma}} \xi^{s}\\ \end{pmatrix}\begin{pmatrix} \sqrt{p\cdot \bar{\sigma}}\xi^{s\dagger} & \sqrt{p\cdot \sigma} \xi^{s\dagger} \end{pmatrix}\\ &=\sum_s \xi^s\xi^{s\dagger} \begin{pmatrix} \sqrt{p\cdot\sigma}\sqrt{p\cdot \bar{\sigma}} & \sqrt{p\cdot\sigma}\sqrt{p\cdot\sigma}\\ \sqrt{p\cdot\bar{\sigma}}\sqrt{p\cdot \bar{\sigma}} & \sqrt{p\cdot \bar{\sigma}}\sqrt{p\cdot \sigma}\\ \end{pmatrix}\\ &= \begin{pmatrix} m & p\cdot\sigma\\ p\cdot \bar{\sigma} & m\\ \end{pmatrix} = \gamma\cdot p + m \end{aligned} \tag{16}

对于反粒子波函数可以得到：

∑svs(p)vˉs(p)=γ⋅p−m(17)\sum_s v^s(p)\bar{v}^s(p) = \gamma\cdot p - m \tag{17}

以及：

∑suˉs(p)us(p)=∑s(p⋅σˉξs†p⋅σξs†)(p⋅σξsp⋅σˉξs)=2p⋅σp⋅σˉ=2m∑svˉs(p)vs(p)=2m(18)\begin{aligned} \sum_s \bar{u}^s(p) u^s(p) &= \sum_s \begin{pmatrix} \sqrt{p\cdot \bar{\sigma}}\xi^{s\dagger} & \sqrt{p\cdot \sigma} \xi^{s\dagger} \end{pmatrix}\begin{pmatrix} \sqrt{p\cdot \sigma} \xi^{s}\\ \sqrt{p\cdot \bar{\sigma}} \xi^{s}\\ \end{pmatrix}\\ &= 2\sqrt{p\cdot\sigma}\sqrt{p\cdot \bar{\sigma}} = 2m\\ \sum_s \bar{v}^s(p) v^s(p) &= 2m\\ \end{aligned}\tag{18}

其他讨论

Wely 方程

注意到生成元 SμνS^{\mu\nu} 是分块对角的，所以洛伦兹群的 Wely 表示是 可约 的。这样们可以把 Dirac 旋量写为：

ψ=(ψLψR)(19)\psi = \begin{pmatrix} \psi_L\\ \psi_R\\ \end{pmatrix}\tag{19}

ψL(ψR)\psi_L(\psi_R) 称为 左手/右手 Dirac 旋量 left-handed(right-handed) Wely spinor。

Dirac 旋量的无穷小变换形式为：

ψ→(1−i2ωμνSμν)ψ\psi \rightarrow (1 - \frac{i}{2}\omega_{\mu\nu}S^{\mu\nu})\psi

得到 ψL\psi_L 与 ψR\psi_R 将遵从不一样的变换法则：

ψL→(1−iθ⋅σ2−β⋅σ2)ψLψR→(1−iθ⋅σ2+β⋅σ2)ψR(20)\begin{aligned} &\psi_L \rightarrow (1 - i\bm{\theta}\cdot\frac{\bm{\sigma}}{2}-\bm{\beta}\cdot\frac{\bm{\sigma}}{2})\psi_L\\ &\psi_R \rightarrow (1 - i\bm{\theta}\cdot\frac{\bm{\sigma}}{2}+\bm{\beta}\cdot\frac{\bm{\sigma}}{2})\psi_R\\ \end{aligned}\tag{20}

Dirac 方程可写为：

(iγμ∂μ−m)ψ=(−mi(∂0+σ⋅∇)i(∂0−σ⋅∇)m)(ψLψR)=0(i\gamma^{\mu}\partial_{\mu}-m)\psi = \begin{pmatrix} -m & i(\partial_0 + \bm{\sigma}\cdot\nabla)\\ i(\partial_0 - \bm{\sigma}\cdot\nabla) & m\\ \end{pmatrix}\begin{pmatrix} \psi_L\\ \psi_R\\ \end{pmatrix} = 0

利用 σμ\sigma^{\mu}，得到：

(−miσ⋅∂iσˉ⋅∂m)(ψLψR)=0\begin{pmatrix} -m & i\sigma\cdot\partial\\ i\bar{\sigma}\cdot\partial & m\\ \end{pmatrix}\begin{pmatrix} \psi_L\\ \psi_R\\ \end{pmatrix} = 0

当 m=0m=0 时，上述方程的左手旋量与右手旋量不会耦合在一起，此时我们得到：

{iσ⋅∂ψL=0iσˉ⋅∂ψR=0(21)\left\{ \begin{aligned} i\sigma\cdot\partial \psi_L=0\\ i\bar{\sigma}\cdot\partial \psi_R=0\\ \end{aligned} \right.\tag{21}

这称为 Wely 方程，这是处理中微子的基本方程。

自旋

在薛定谔方程中：自由粒子的哈密顿量为

H=p^22mH = \frac{\hat{\bm{p}}^2}{2m}

其与角动量算子 L^=r^×p^\hat{\bm{L}} = \hat{\bm{r}}\times\hat{\bm{p}} 对易，这说明:薛定谔方程给出自由粒子的角动量是守恒的。但是，在量子力学中，我们指出粒子除了轨道角动量（即 L\bm{L}）之外，还有内禀角动量，我们称之为 自旋。对于自由粒子来说，应当是自旋角动量与轨道角动量相加得到的总角动量守恒。薛定谔方程完全无法解释自旋的存在。

现在，我们来考虑 Dirac 方程对自旋的解释。在 Dirac 方程中，自由粒子的哈密顿量为：

HD=α⋅p^+βm(22)H_D = \bm{\alpha}\cdot\hat{\bm{p}} + \beta m \tag{22}

首先计算 H^D\hat{H}_D 与 L^\hat{\bm{L}} 的对易关系，来看看 Dirac 方程对于自由粒子是否给出轨道角动量守恒。

[H^D,L^]=[α⋅p^+βm,εijkx^ip^je^k]=[αlp^l,εijkx^ip^je^k]=αl[p^l,x^i]p^jεijke^k=−iαlδilp^jεijke^k=−iαip^jεijke^k=−iα×p^\begin{aligned} [\hat{H}_D,\hat{\bm{L}}] &= [\bm{\alpha}\cdot\hat{\bm{p}} + \beta m,\varepsilon_{ijk}\hat{x}_i\hat{p}_j\hat{\bm{e}}_k]\\ &=[\alpha_l\hat{p}_l,\varepsilon_{ijk}\hat{x}_i\hat{p}_j\hat{\bm{e}}_k]\\ & = \alpha_l [\hat{p}_l,\hat{x}_i]\hat{p}_j\varepsilon_{ijk}\hat{\bm{e}}_k\\ & = -i\alpha_l\delta_{il}\hat{p}_j\varepsilon_{ijk}\hat{\bm{e}}_k\\ & = -i\alpha_i\hat{p}_j\varepsilon_{ijk}\hat{\bm{e}}_k\\ & = -i \bm{\alpha}\times \hat{\bm{p}} \end{aligned}

此时轨道角动量不守恒。考虑构造如下算子：

S^≡12Σ^=12(σ00σ)(23)\hat{\bm{S}} \equiv \frac{1}{2}\hat{\bm{\Sigma}} = \frac{1}{2}\begin{pmatrix} \bm{\sigma} & 0\\ 0 & \bm{\sigma}\\ \end{pmatrix} \tag{23}

这就是 rotation 对应的生成元。

Pauli-Dirac 表象下的 α\alpha 矩阵与从泡利矩阵推出的 Σ\Sigma 矩阵具有如下对易关系：

[αi,Σj]=(0σiσi0)(σj00σj)−(σj00σj)(0σiσi0)=(0[σi,σj][σi,σj]0)=(02iεijkσk2iεijkσk0)=2iεijkαk(24)\begin{aligned} [\alpha_i,\Sigma_j] &= \begin{pmatrix} 0 & \sigma_i\\ \sigma_i & 0\\ \end{pmatrix}\begin{pmatrix} \sigma_j & 0\\ 0 & \sigma_j\\ \end{pmatrix} - \begin{pmatrix} \sigma_j & 0\\ 0 & \sigma_j\\ \end{pmatrix}\begin{pmatrix} 0 & \sigma_i\\ \sigma_i & 0\\ \end{pmatrix}\\ & = \begin{pmatrix} 0 & [\sigma_i,\sigma_j]\\ [\sigma_i,\sigma_j] & 0\\ \end{pmatrix}\\ & = \begin{pmatrix} 0 & 2i\varepsilon_{ijk} \sigma_k \\ 2i\varepsilon_{ijk} \sigma_k & 0\\ \end{pmatrix}\\ & = 2i\varepsilon_{ijk}\alpha_k \tag{24} \end{aligned}

另外，容易得到 [β,Σi]=0[\beta,\Sigma_i] = 0

如此，考虑 S^\hat{\bm{S}} 与 H^D\hat{H}_D 的对易关系：

[H^D,S^]=[α⋅p^,12Σ^]=[αip^i,12Σje^j]=12[αi,Σj]p^ie^j=iεijkαkp^ie^j=iα×p^(25)\begin{aligned} [\hat{H}_D,\hat{\bm{S}}] &= [\bm{\alpha}\cdot\hat{\bm{p}},\frac{1}{2}\hat{\bm{\Sigma}}]\\ & = [\alpha_i\hat{\bm{p}}_i, \frac{1}{2}\Sigma_j \hat{\bm{e}}_j]\\ &=\frac{1}{2}[\alpha_i,\Sigma_j ]\hat{\bm{p}}_i\hat{\bm{e}}_j\\ &= i\varepsilon_{ijk}\alpha_k\hat{\bm{p}}_i\hat{\bm{e}}_j\\ &= i \bm{\alpha}\times\hat{\bm{p}} \end{aligned}\tag{25}

如此，我们发现由 Dirac 方程可以得到：

[H^D,L^+S^]=0(26)[\hat{H}_D,\hat{\bm{L}}+\hat{\bm{S}}]=0 \tag{26}

于是 S^\bm{\hat{S}} 给出了自旋角动量，总角动量 J=L+S\bm{J} = \bm{L}+\bm{S} 是守恒的。实际上，是 Dirac 方程的旋量结构导致了自旋的存在。在 (23)(23) 式中，我们引入的 12\frac{1}{2} 这个因子其实说明其自旋为 12\frac{1}{2}，Dirac 方程是描述自旋 12\frac{1}{2} 费米子的方程。

自旋磁矩

对于电子来说，轨道角动量的磁矩同轨道角动量具有以下关系：

μ=q2mL\bm{\mu} = \frac{q}{2m}\bm{L}

但是这一点并不能推广到自旋角动量同自旋角动量的关系。实验给出：

μ=gq2mS(27)\bm{\mu} = g\frac{q}{2m}\bm{S} \tag{27}

gg 称为 g-factor。对于电子来说，有：

ge=2.00231930436256(35)g_e = 2.00231930436256(35)

这也是薛定谔方程所不能解释的。下面我们介绍，Dirac 方程将预测 g=2g = 2。在量子电动力学中，我们会得到关于 gg 更精确的计算。

考虑电磁相互作用的 Dirac 方程写为：

(α⋅(p^−qA)+βm)ψ=(E−qϕ)ψ(28)(\bm{\alpha}\cdot(\hat{\bm{p}}- q\bm{A}) + \beta m)\psi = (E-q\phi)\psi \tag{28}

写为矩阵形式：

((E−m−qϕ)I−σ⋅(p^−qA)−σ⋅(p^−qA)(E+m−qϕ)I)(ψLψR)=0(29)\begin{pmatrix} (E-m-q\phi)I & -\bm{\sigma}\cdot(\hat{\bm{p}} - q\bm{A}) \\ -\bm{\sigma}\cdot(\hat{\bm{p}} - q\bm{A}) & (E+m-q\phi)I\\ \end{pmatrix} \begin{pmatrix} \psi_L\\ \psi_R\\ \end{pmatrix} = 0 \tag{29}

将 (22)(22) 写作如下方程组：

{[σ⋅(p^−qA)]ψR=(E−m−qϕ)ψL[σ⋅(p^−qA)]ψL=(E+m−qϕ)ψR(30)\left\{ \begin{aligned} [\bm{\sigma} \cdot (\hat{\bm{p}} - q\bm{A})]\psi_R = (E-m - q\phi)\psi_L\\ [\bm{\sigma} \cdot (\hat{\bm{p}} - q\bm{A})]\psi_L = (E + m - q\phi)\psi_R\\ \end{aligned} \right.\tag{30}

在非相对论极限下有 E≈m≫qϕE\approx m \gg q\phi，因此可得：

ψR≈12m[σ⋅(p^−qA)]ψL\psi_R \approx \frac{1}{2m}[\bm{\sigma} \cdot (\hat{\bm{p}} - q\bm{A})]\psi_L

得到：

(E−m−qϕ)ψL=12m[σ⋅(p^−qA)]2ψL=12m{(p^−qA)2+iσ⋅[(p^−qA)×(p^−qA)]}ψL=12m[(p^−qA)2−iqσ⋅(p^×A+A×p^)]ψL=12m[(p^−qA)2−qσ⋅(∇×A+A×∇)]ψL=12m(p^−qA)2ψL−12mqσ⋅(∇×(AψL)+A×(∇ψL))=12m(p^−qA)2ψL−12mqσ⋅(∇×A)ψL=12m(p^−qA)2ψL−12mqσ⋅BψL\begin{aligned} (E-m - q\phi)\psi_L &= \frac{1}{2m}[\bm{\sigma} \cdot (\hat{\bm{p}} - q\bm{A})]^2 \psi_L\\ &= \frac{1}{2m}\{(\hat{\bm{p}} - q\bm{A})^2 + i\bm{\sigma}\cdot[(\hat{\bm{p}} - q\bm{A})\times (\hat{\bm{p}} - q\bm{A})]\}\psi_L\\ &= \frac{1}{2m}[(\hat{\bm{p}} - q\bm{A})^2 - iq\bm{\sigma}\cdot(\hat{\bm{p}}\times\bm{A} + \bm{A}\times\hat{\bm{p}})]\psi_L\\ &= \frac{1}{2m}[(\hat{\bm{p}} - q\bm{A})^2 - q\bm{\sigma}\cdot(\nabla\times\bm{A} + \bm{A}\times\nabla)]\psi_L\\ & = \frac{1}{2m}(\hat{\bm{p}} - q\bm{A})^2\psi_L - \frac{1}{2m} q\bm{\sigma}\cdot(\nabla\times(\bm{A}\psi_L) + \bm{A}\times(\nabla\psi_L))\\ &= \frac{1}{2m}(\hat{\bm{p}} - q\bm{A})^2\psi_L - \frac{1}{2m} q\bm{\sigma}\cdot(\nabla\times\bm{A})\psi_L\\ &= \frac{1}{2m}(\hat{\bm{p}} - q\bm{A})^2\psi_L - \frac{1}{2m} q\bm{\sigma}\cdot\bm{B}\psi_L\\ \end{aligned}

上述推导用到公式：

(σ⋅a)(σ⋅b)=(a⋅b)I+iσ⋅(a×b)(\bm{\sigma}\cdot\bm{a})(\bm{\sigma}\cdot\bm{b}) = (\bm{a}\cdot\bm{b})I + i\bm{\sigma}\cdot(\bm{a}\times\bm{b})

证明：

(σ⋅a)(σ⋅b)=σiaiσjbj=aibjσiσj=12aibj([σi,σj]+{σi,σj})=12aibj(2iεijkσk+2δijI)=aibjδijI+iεijkaibjσk=(a⋅b)I+iσ⋅(a×b)\begin{aligned} (\bm{\sigma}\cdot\bm{a})(\bm{\sigma}\cdot\bm{b}) &= \sigma_ia_i\sigma_jb_j\\ & = a_ib_j\sigma_i \sigma_j\\ & = \frac{1}{2}a_ib_j ( [\sigma_i,\sigma_j] + \{\sigma_i,\sigma_j\})\\ & = \frac{1}{2}a_ib_j (2i\varepsilon_{ijk}\sigma_k + 2\delta_{ij}I)\\ & = a_ib_j\delta_{ij}I + i\varepsilon_{ijk}a_ib_j\sigma_k\\ & = (\bm{a}\cdot\bm{b})I + i\bm{\sigma}\cdot(\bm{a}\times\bm{b})\\ \end{aligned}

综上，我们得到：

EψL=[m+12m(p^−qA)2+qϕ−q2m(σ⋅B)]ψR(31)E\psi_L = [m + \frac{1}{2m}(\hat{\bm{p}} - q\bm{A})^2 + q\phi - \frac{q}{2m}(\bm{\sigma}\cdot\bm{B})]\psi_R\tag{31}

上式右边各项分别对应静能量、动能、电势能和磁矩在磁场中的能量。对比电磁学中磁矩的能量表达式：

U=−μ⋅BU = -\bm{\mu}\cdot\bm{B}

如此得到自旋磁矩为：

μ=qσ2m=qmS⇒g=2(32)\bm{\mu} = \frac{q\bm{\sigma}}{2m} = \frac{q}{m}\bm{S}\Rightarrow g=2 \tag{32}

对 g=2g=2 的预言是 Dirac 方程的成功之处之一。

Dirac 矩阵与 Dirac 双线性映射

我们之前得到 ψˉψ\bar{\psi}\psi 是一个洛伦兹标量。而 ψˉγμψ\bar{\psi}\gamma^{\mu}\psi 在洛伦兹变换下有：

ψˉγμψ→ψˉΛ12−1γμΛ12ψ=Λ  νμψˉγνψ\bar{\psi}\gamma^{\mu}\psi \rightarrow \bar{\psi}\Lambda_{\frac{1}{2}}^{-1}\gamma^{\mu}\Lambda_{\frac{1}{2}}\psi = \Lambda^{\mu}_{\ \ \nu}\bar{\psi}\gamma^{\nu}\psi

即 ψˉγμψ\bar{\psi}\gamma^{\mu}\psi 为一个洛伦兹矢量。这样的构造称为 Dirac 双线性映射 Dirac Field Bilinear。所谓双线性，是指：

ψˉγμ(αψ1+βψ2)=αψˉγμψ1+βψˉγμψ2αψ1+βψ2‾γμψ=α∗ψˉ1γμψ+β∗ψˉ2γμψ\begin{aligned} \bar{\psi}\gamma^{\mu}(\alpha\psi_1+\beta\psi_2) = \alpha\bar{\psi}\gamma^{\mu}\psi_1 + \beta\bar{\psi}\gamma^{\mu}\psi_2\\ \overline{\alpha\psi_1+\beta\psi_2}\gamma^{\mu}\psi = \alpha^*\bar{\psi}_1\gamma^{\mu}\psi + \beta^*\bar{\psi}_2\gamma^{\mu}\psi\\ \end{aligned}

。现在我们想问对于一个任意的 4×44\times 4 矩阵 Γ\Gamma，ψˉΓψ\bar{\psi}\Gamma\psi 的性质如何呢？我们可以选取一组特定的基底去表示 Γ\Gamma，那么就可以将 ψˉΓψ\bar{\psi}\Gamma\psi 分解成一系列按照确定规则分解的项。对于一个任意 4×44\times 4 的复矩阵来说，可以选取 1616 个矩阵作为基底，以复系数进行线性组合得到。利用 γ\gamma 矩阵构造如下矩阵作为基底：

114γμ6γμν=12[γμ,γν]≡γ[μγν]≡−iσμν4γμνρ=γ[μγνγρ]1γμνρσ=γ[μγνγργσ](33)\begin{aligned} 1\qquad&1\\ 4\qquad&\gamma^{\mu}\\ 6\qquad&\gamma^{\mu\nu} = \frac{1}{2}[\gamma^{\mu},\gamma^{\nu}] \equiv \gamma^{[\mu}\gamma^{\nu]} \equiv -i\sigma^{\mu\nu}\\ 4\qquad& \gamma^{\mu\nu\rho} = \gamma^{[\mu}\gamma^{\nu}\gamma^{\rho]}\\ 1\qquad& \gamma^{\mu\nu\rho\sigma} = \gamma^{[\mu}\gamma^{\nu}\gamma^{\rho}\gamma^{\sigma]}\\ \end{aligned}\tag{33}

将指标用方括号括起来含义为：对这些指标进行反对称化处理。

一共有 1616 个矩阵。对于其中任意一个矩阵构成的 Dirac 双线性映射，都容易得到其变换规则，例如：

ψˉγμνψ→ψˉΛ12−112[γμγν−γνγμ]Λ12ψ=ψˉ12[Λ12−1γμΛ12−1Λ12γνΛ12−Λ12−1γνΛ12−1Λ12γμΛ12]ψ=Λ  αμΛ  βνψˉγαβψ(34)\begin{aligned} \bar{\psi}\gamma^{\mu\nu}\psi &\rightarrow \bar{\psi}\Lambda_{\frac{1}{2}}^{-1}\frac{1}{2}[\gamma^{\mu}\gamma^{\nu}-\gamma^{\nu}\gamma^{\mu}]\Lambda_{\frac{1}{2}}\psi\\ & = \bar{\psi}\frac{1}{2}[\Lambda_{\frac{1}{2}}^{-1}\gamma^{\mu}\Lambda_{\frac{1}{2}}^{-1}\Lambda_{\frac{1}{2}}\gamma^{\nu}\Lambda_{\frac{1}{2}}-\Lambda_{\frac{1}{2}}^{-1}\gamma^{\nu}\Lambda_{\frac{1}{2}}^{-1}\Lambda_{\frac{1}{2}}\gamma^{\mu}\Lambda_{\frac{1}{2}}]\psi\\ &= \Lambda^{\mu}_{\ \ \alpha}\Lambda^{\nu}_{\ \ \beta}\bar{\psi}\gamma^{\alpha\beta}\psi\\ \end{aligned}\tag{34}

这表现为一个二阶逆变洛伦兹张量。

通过定义 γ5\gamma^5：

γ5≡iγ0γ1γ2γ3=−i4!ϵμνρσγμγνγργσ(35)\gamma^5 \equiv i\gamma^0\gamma^1\gamma^2\gamma^3 = -\frac{i}{4!}\epsilon^{\mu\nu\rho\sigma}\gamma_{\mu}\gamma_{\nu}\gamma_{\rho}\gamma_{\sigma}\tag{35}

可以将 (33)(33) 的后两组基底改写为：

γμνρσ=−iϵμνρσγ5γμνρ=−iϵμνρσγσγ5\gamma^{\mu\nu\rho\sigma} = -i\epsilon^{\mu\nu\rho\sigma}\gamma^5\quad \gamma^{\mu\nu\rho} = -i\epsilon^{\mu\nu\rho\sigma}\gamma_{\sigma}\gamma^5

γ5\gamma^5 具有性质：

(γ5)†=γ5(γ5)2=1{γ5,γμ}=0\begin{aligned} &(\gamma^5)^{\dagger} = \gamma^5\\ &(\gamma^5)^2 = 1\\ &\{\gamma^{5},\gamma^{\mu}\} = 0\\ \end{aligned}

引入 γ5\gamma^5，我们将这 16 个基底重写在下面的表格中：

表达式 性质 数量
11 标量 11
γμ\gamma^{\mu} 矢量 44
σμν=i2[γμ,γν]\sigma^{\mu\nu} = \frac{i}{2}[\gamma^{\mu},\gamma^{\nu}] 张量 66
γμγ5\gamma^{\mu}\gamma^5 赝矢量 44
γ5\gamma^{5} 赝标量 11

所谓赝矢量/赝标量是指其在洛伦兹变换下与矢量/标量的变换规则相同，而在宇称变换下得到的结果与矢量/标量相比改变符号。

按照同样方式可以构造 Dirac 双线性映射：

jμ=ψˉγμψjμ5=ψˉγμγ5ψ\begin{aligned} j^{\mu} = \bar{\psi}\gamma^\mu\psi \quad j^{\mu5} = \bar{\psi}\gamma^\mu\gamma^5\psi \end{aligned}

如果 ψ\psi 满足 Dirac 方程，容易得到：

∂μjμ=0\begin{aligned} \partial_{\mu}j^{\mu} &= 0 \end{aligned}

即 jμj^{\mu} 成为守恒量。当我们将 Dirac 场与电磁场耦合在一起时，jμj^{\mu} 成为电流密度。

另外有：

∂μjμ5=2imψˉγ5ψ\partial_{\mu}j^{\mu5} = 2im\bar{\psi}\gamma^5\psi

当 m=0m=0 时，jμ5j^{\mu5} 是守恒的（称为 轴矢流 axial vector current）。

以上两个守恒流分别与系统的如下变换对应的对称性有关：

  1. U(1)U(1) 变换

ψ(x)→eiαψ(x)\psi(x) \rightarrow e^{i\alpha}\psi(x)

  1. 手征变换 Chiral Transformation

ψ(x)→eiαγ5ψ(x)\psi(x) \rightarrow e^{i\alpha\gamma^5}\psi(x)

为了进行 Dirac 双线性映射乘积的计算。我们需要了解 Fierz identities 的相关知识。其核心为以下等式：

(σμ)αβ(σμ)γδ=2ϵαγϵβδ(36)(\sigma^{\mu})_{\alpha\beta}(\sigma_{\mu})_{\gamma\delta} = 2\epsilon_{\alpha\gamma}\epsilon_{\beta\delta}\tag{36}

对于该等式的验证是很直接的：

∵σμ=(1,σ)σμ=(1,−σ)∴(σμ)00(σμ)11=(σ0)00(σ0)11−(σ3)00(σ3)11=2(σμ)01(σμ)10=−(σ1)01(σ1)10−(σ2)01(σ2)10=−2\begin{aligned} \because& \sigma^{\mu} = (1,\bm{\sigma}) \quad \sigma_{\mu} = (1,-\bm{\sigma})\\ \therefore& (\sigma^{\mu})_{00}(\sigma_{\mu})_{11} = (\sigma^{0})_{00}(\sigma_{0})_{11} - (\sigma^{3})_{00}(\sigma_{3})_{11} = 2\\ & (\sigma^{\mu})_{01}(\sigma_{\mu})_{10} = -(\sigma^{1})_{01}(\sigma_{1})_{10} - (\sigma^{2})_{01}(\sigma_{2})_{10} = -2\\ \end{aligned}

利用该等式，我们可以计算：

(uˉ1Rσμu2R)(uˉ3Rσμu4R)=(uˉ1Rασαβμu2Rβ)(uˉ3Rγσμγδu4Rδ)=2ϵαγϵβδuˉ1Rαu2Rβuˉ3Rγu4Rδ=−2ϵαγϵδβuˉ1Rαu4Rδuˉ3Rγu2Rβ=uˉ1Rασαδμu4Rδuˉ3Rγσμγβu2Rβ=−(uˉ1Rσμu4R)(uˉ3Rσμu2R)\begin{aligned} &(\bar{u}_{1R}\sigma^{\mu}u_{2R})(\bar{u}_{3R}\sigma_{\mu}u_{4R})\\ =&(\bar{u}_{1R\alpha}\sigma^{\mu}_{\alpha\beta}u_{2R\beta})(\bar{u}_{3R\gamma}\sigma_{\mu\gamma\delta}u_{4R\delta})\\ =& 2\epsilon_{\alpha\gamma}\epsilon_{\beta\delta}\bar{u}_{1R\alpha}u_{2R\beta}\bar{u}_{3R\gamma}u_{4R\delta}\\ =&- 2\epsilon_{\alpha\gamma}\epsilon_{\delta\beta}\bar{u}_{1R\alpha}u_{4R\delta}\bar{u}_{3R\gamma}u_{2R\beta}\\ =&\bar{u}_{1R\alpha} \sigma^{\mu}_{\alpha\delta} u_{4R\delta}\bar{u}_{3R\gamma} \sigma_{\mu\gamma\beta} u_{2R\beta}\\ =&-(\bar{u}_{1R}\sigma^{\mu}u_{4R})(\bar{u}_{3R}\sigma_{\mu}u_{2R})\\ \end{aligned}

类似的，常用等式还有以下，都可以直接验证：

(σˉμ)αβ(σˉμ)γδ=2ϵαγϵβδϵαβ(σμ)βγ=(σˉμT)αβϵβγ\begin{aligned} &(\bar{\sigma}^{\mu})_{\alpha\beta}(\bar{\sigma}_{\mu})_{\gamma\delta} = 2\epsilon_{\alpha\gamma}\epsilon_{\beta\delta}\\ &\epsilon_{\alpha\beta}(\sigma^{\mu})_{\beta\gamma} = (\bar{\sigma}^{\mu T})_{\alpha\beta}\epsilon_{\beta\gamma} \end{aligned}