量子场论笔记（五）：Dirac 方程

Dirac 方程

在这里，我们先遵循 Dirac 的工作，找到 Dirac 方程是如何推导出来的，这是一个逻辑上比较自然的过程。

Klein-Gordon 方程的问题

我们之前介绍过 Klein-Gordon 方程：

$(\partial^{\mu}\partial_{\mu}+m^2)\phi = 0 \tag{1}$

之前提到其作为相对论量子力学的基本方程是不自洽的，我们现在来进行具体讨论。
考虑其平面波解为：

$\phi(\bm{x},t) = Ne^{-i(Et-\bm{p}\cdot\bm{x})} \tag{2}$

代入 Klein-Gordon 方程得到：

$E = \pm \sqrt{p^2 + m^2}$

量子力学不允许我们忽略这个负能解，但我们在这里并不清楚负能解的物理意义。在统计力学中，出现负能量是一件我们不能忍受的事情，因为玻尔兹曼因子 $e^{-\beta E}$ 启发我们，此时所有粒子都处于能量趋于 $-\infty$ 的态上。我们称其为 负能量问题。

其次，利用 Klein-Gordon 方程可以得到：

$\begin{aligned} \phi^* \frac{\partial^2 \phi}{\partial t^2} - \phi \frac{\partial^2 \phi^*}{\partial t^2} &= \phi^* (\nabla^2 \phi - m^2 \phi) - \phi (\nabla^2 \phi^* - m^2 \phi^*)\\ &= \phi^*\nabla^2\phi - \phi \nabla^2\phi^*\\ &= \nabla\cdot (\phi^*\nabla \phi - \phi\nabla \phi^*) = \frac{\partial}{\partial t}(\phi^*\frac{\partial \phi}{\partial t} - \phi \frac{\partial \phi^*}{\partial t}) \end{aligned}\tag{3}$

对比流守恒方程：

$\frac{\partial \rho}{\partial t} + \nabla\cdot \bm{j} = 0\tag{4}$

我们可以定义：

$\begin{aligned} \rho &= i(\phi^*\frac{\partial \phi}{\partial t} - \phi \frac{\partial \phi^*}{\partial t})\\ \bm{j} &= -i(\phi^*\nabla \phi - \phi\nabla \phi^*)\\ \end{aligned}\tag{5}$

代入平面波波函数 $(2)$ ，可得：

$\rho = 2|N|^2E,\quad \bm{j} = 2|N|^2\bm{p} \tag{6}$

那么负能解会导致负几率的出现，这更难理解。这称为 负几率问题。

Dirac 方程

为了解决负能量与负几率问题，Dirac 认为是二次的质能关系使得 Klein-Gordon 方程成为一个二阶方程，这导致了上述问题的出现。Dirac 想找到一个一次的质能关系：

$E = \sqrt{p^2+m^2}$

上述的右边是需要进行开平方操作的，如何处理呢？Dirac 创造性的写出下列式子：

$E = \bm{\alpha}\cdot\bm{p} + \beta m$

并要求：

$\begin{aligned} E^2 &= (\bm{\alpha}\cdot\bm{p} + \beta m)^2\\ &= \sum_{ij}\alpha_i\alpha_jp_ip_j + \sum_i (\alpha_i\beta + \beta\alpha_i) p_i m + \beta^2m^2\\ &= p^2+m^2 \end{aligned}$

对应的系数有如下关系：

$\begin{aligned} &\alpha_x^2 = \alpha_y^2 = \alpha_z^2 = \beta^2 = 1\\ &\alpha_j\beta + \beta \alpha_j = 0\\ &\alpha_j\alpha_k + \alpha_k\alpha_j = 0,\quad(j\neq k)\\ \end{aligned} \tag{7}$

显然 $\alpha_x,\alpha_y,\alpha_z,\beta$ 不可能是一些普通的数，而是矩阵。具体来说，它们是四个互相反对易且平方为单位阵的矩阵。

这样的矩阵还具有以下性质：

零迹

$\mathrm{tr}(\alpha_i) = \mathrm{tr}(\beta) = 0$

$\mathrm{tr}(\alpha_i) = \mathrm{tr}(\alpha_i\beta\beta) = -\mathrm{tr}(\beta\alpha_i\beta) = -\mathrm{tr}(\alpha_i\beta\beta) = -\mathrm{tr}(\alpha_i)$

本征值为 $\pm 1$

不妨考虑 $\alpha_x$ 的本征值为 $\lambda$ 的向量为 $\omega$ ，可得：

$\begin{aligned} &(\alpha_x)^2\omega = I\omega = \omega\\ &(\alpha_x)^2\omega = \alpha_x(\alpha_x\omega) = \lambda^2 \omega\\ \Rightarrow & \lambda = \pm 1 \end{aligned}$
厄密

$\alpha_i^\dagger = \alpha_i,\quad \beta^\dagger = \beta$

这点从本征值都是实数就能得到。

考虑到本征值为 $\pm 1$ ，且迹是零。则这些矩阵必定是偶数维的。 $2$ 维情况下，互相反对易的矩阵为泡利矩阵，但泡利矩阵只有三个，我们要找到四个互相反对易的矩阵。如此，最低的维数为 $4$ 。

$(7)$ 式实际完全确定了矩阵 $\{\alpha_i,\beta\}$ 的代数结构。但使用特定形式的矩阵进行表示是很方便的。例如在 Dirac-Pauli 表象 下，有：

$\beta = \begin{pmatrix} I & 0 \\ 0 & -I \\ \end{pmatrix},\quad \alpha_i = \begin{pmatrix} 0 & \sigma_i \\ \sigma_i & 0 \\ \end{pmatrix}\tag{8}$

可以验证其满足 $(7)$ 的关系。

现在将这个一次质能关系进行一次量子化，得到如下方程：

$\hat{E}\psi = (\alpha\cdot\hat{\bm{p}} + \beta m)\psi \tag{9}$

在坐标表象下，得到：

$i\frac{\partial \psi}{\partial t} = (-i\bm{\alpha}\cdot \nabla + \beta m )\psi \tag{10}$

这就是 Dirac 方程。在 $\alpha,\beta$ 的维数为 $4$ 时， $\psi$ 应当是一个有四个分量的列向量。

$\psi = \begin{pmatrix} \psi_1\\ \psi_2\\ \psi_3\\ \psi_4\\ \end{pmatrix}\tag{11}$

我们称其为 Dirac 旋量 Driac spinor。

我们发现 Dirac 方程确实解决了 Klein-Gordon 方程中的一些问题。

由 Dirac 方程：

$-i\alpha_x\frac{\partial \psi}{\partial x}-i\alpha_y\frac{\partial \psi}{\partial y}-i\alpha_z\frac{\partial \psi}{\partial z}+m\beta\psi = i\frac{\partial \psi}{dt} \tag{12}$

和其共轭形式：

$+i\frac{\partial \psi^\dagger}{\partial x}\alpha^\dagger_x+i\frac{\partial \psi^\dagger}{\partial y}\alpha^\dagger_y+i\frac{\partial \psi^\dagger}{\partial z}\alpha^\dagger_z+m\psi^\dagger \beta^\dagger = -i\frac{\partial \psi^\dagger}{dt} \tag{13}$

$(12)$ 式左乘 $\psi^\dagger$ ， $(13)$ 式右乘 $\psi$ ，其结果相减，得到：

$-i\frac{\partial (\psi^\dagger \alpha_x \psi)}{\partial x}-i\frac{\partial (\psi^\dagger \alpha_y \psi)}{\partial y}-i\frac{\partial (\psi^\dagger \alpha_z \psi)}{\partial z} = i \frac{\partial (\psi^\dagger\psi)}{\partial t}$

即为：

$\nabla\cdot(\psi^\dagger \bm{\alpha}\psi) + \frac{\partial (\psi^\dagger\psi)}{\partial t} = 0 \tag{14}$

对比流守恒方程，有：

$\bm{j} = \psi^\dagger \bm{\alpha} \psi,\quad \rho = \psi^\dagger\psi \tag{15}$

对于 Dirac spinor 来说：

$\rho = |\psi_1|^2 + |\psi_2|^2 + |\psi_3|^2 + |\psi_4|^2 \tag{16}$

此时 Klein-Gordon 方程出现的负几率问题已经不会出现了。但是对于负能解问题，Dirac 方程仍然没有解决。实际上，负能解其实暗示着反粒子的存在，这一点我们之后再讨论。

洛伦兹不变的方程

现在我们从另一个角度出发，来推导 Dirac 方程。

洛伦兹群的表示

我们在上一篇中讨论过洛伦兹变换，我们现在来看洛伦兹变换如何作用于场量。谈及变换对对象的作用，可以从两种角度来看：

主动观点：坐标系不变，对物体进行变换

被动观点：物体不变，对坐标系进行变换

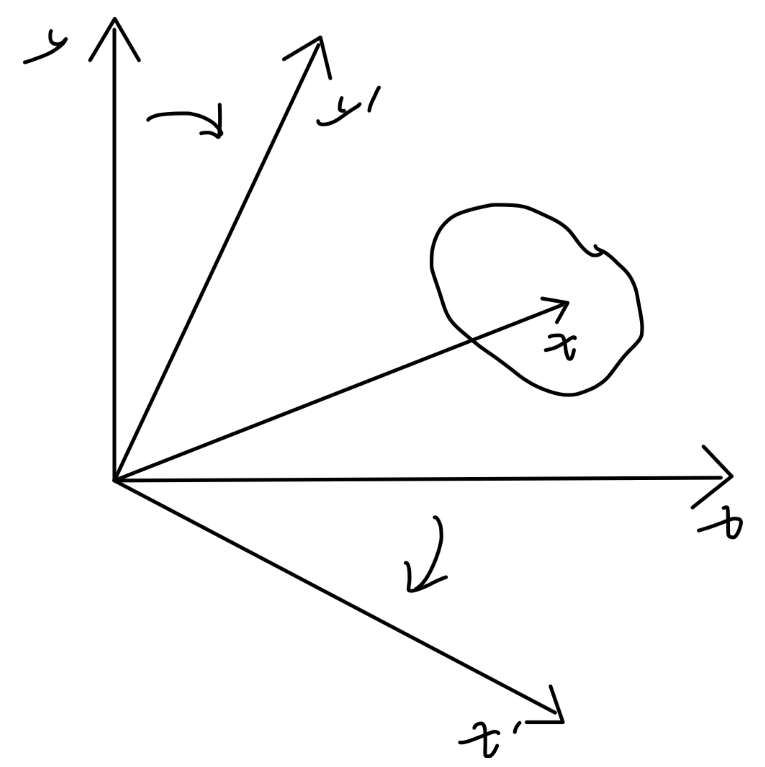
我们下面均采用主动观点。

对于 标量场 scalar field $\phi(x)$ 来说， $\phi$ 说明这个对象是标量、而 $\phi$ 对 $x$ 的依赖给出了这个标量的分布。一个标量在变换下是不变的，但是分布会变化：考虑原来在 $x$ 处有一极大值点，经过洛伦兹变换 $\Lambda$ 后，极大值点应当是 $\Lambda x$ ，所以标量场的变换应当为以下形式：

$\phi \rightarrow \phi'(x') = \phi(\Lambda^{-1}x)$

对于 矢量场 vector field $A^{\mu}(x)$ 来说，不仅仅分布发生了变化，由于矢量场在每一点的取值作为一个矢量也应当在洛伦兹变换下发生变化。

因此有：

$A^{\mu}(x)\rightarrow \Lambda^{\mu}_{\ \ \nu}A^{\nu}(\Lambda^{-1}x)$

一般的张量场的变换为：

$T^{\mu\nu\cdots}_{\quad \rho\sigma \cdots}(x) \rightarrow \Lambda^{\mu}_{\ \ \mu'}\Lambda^{\nu}_{\ \ \nu'}\cdots \Lambda_{\rho}^{\ \ \rho'}\Lambda_{\sigma}^{\ \ \sigma'}T^{\mu'\nu'\cdots}_{\quad \rho'\sigma' \cdots}(\Lambda^{-1}x)$

对于标量场的偏导数：

$\partial_{\mu}\phi(x) \rightarrow \partial_{\mu}(\phi(\Lambda^{-1}x)) = \Lambda_{\mu}^{\ \ \nu}(\partial_{\nu}\phi)(\Lambda^{-1}x)$

可以看出，协变导数 $\partial_{\mu}$ 遵从协变矢量的变换规则。

一般的，我们谈论某个对象在洛伦兹变换下怎么变，实际上就是找到洛伦兹群对应的表示。

我们现在考虑一个具有 $n$ 个分量的列向量 $\psi$ ，称为 multiplet。对 multiplet 的洛伦兹变换实际上我们只要找到洛伦兹群的 $n$ 维表示。这个问题等价于找到一些 $n\times n$ 的矩阵 $J^{\mu\nu}$ ，它们具有洛伦兹代数的结构：

$[J^{\mu\nu},J^{\rho\sigma}] = i(g^{\nu\rho}J^{\mu\sigma}-g^{\mu\rho}J^{\nu\sigma}-g^{\nu\sigma}J^{\mu\rho}+g^{\mu\sigma}J^{\nu\rho}) \tag{17}$

那么我们就可以用这些矩阵作为生成元，得到 $\psi$ 的变换规则：

$\psi \rightarrow U(\Lambda)\psi = \exp(-\frac{i}{2}\omega_{\mu\nu}J^{\mu\nu})\psi$

对于 $n=4$ ，我们在上一篇中已经找到了一组表示：

$(\mathcal{J}^{\mu\nu})^{\rho}_{\ \ \sigma} = i(g^{\mu\rho}\delta^{\nu}_{\ \ \sigma}-g^{\nu\rho}\delta^{\mu}_{\ \ \sigma}) \tag{18}$

有：

$\Lambda^{\rho}_{\ \ \sigma} = \exp(-\frac{i}{2}\omega_{\mu\nu}\mathcal{J}^{\mu\nu})^{\rho}_{\ \ \sigma}$

无穷小形式为：

$\Lambda^{\rho}_{\ \ \sigma} =1 -\frac{i}{2}\omega_{\mu\nu}(\mathcal{J}^{\mu\nu})^{\rho}_{\ \ \sigma} \tag{19}$

对于任意 $n$ 的取值，Dirac “天才般的” 找到了一系列矩阵满足 $(17)$ 。他是这样构造的：
如果我们能找到 $4$ 个满足特定 反对易关系 的 $n\times n$ 矩阵 $\gamma^{\mu}$ ，即满足：

$\{\gamma^{\mu},\gamma^{\nu}\} \equiv \gamma^{\mu}\gamma^{\nu} + \gamma^{\nu}\gamma^{\mu} = 2g^{\mu\nu}\times 1_{n\times n}\tag{20}$

那么：

$S^{\mu\nu} = \frac{i}{4}[\gamma^{\mu},\gamma^{\nu}] \tag{21}$

是洛伦兹群的生成元。 $\gamma^{\mu}$ 称为 Dirac 矩阵。

我们作出如下验证：

$\begin{aligned} [S^{\mu\nu},S^{\rho\sigma}] &= -\frac{1}{16}[[\gamma^{\mu},\gamma^{\nu}],[\gamma^{\rho},\gamma^{\sigma}]]\\ &= -\frac{1}{16}[\{\gamma^{\mu},\gamma^{\nu}\} - 2\gamma^{\nu}\gamma^{\mu},\{\gamma^{\rho},\gamma^{\sigma}\} - 2\gamma^{\sigma}\gamma^{\rho}]\\ &= -\frac{1}{16}[2g^{\mu\nu} - 2\gamma^{\nu}\gamma^{\mu},2g^{\rho\sigma} - 2\gamma^{\sigma}\gamma^{\rho}]\\ &= -\frac{1}{4}[\gamma^{\nu}\gamma^{\mu},\gamma^{\sigma}\gamma^{\rho}]\\ &= -\frac{1}{4}(\gamma^{\nu}\gamma^{\mu}\gamma^{\sigma}\gamma^{\rho}-\gamma^{\sigma}\gamma^{\rho}\gamma^{\nu}\gamma^{\mu})\\ &= -\frac{1}{4}(\gamma^{\nu}\gamma^{\mu}\gamma^{\sigma}\gamma^{\rho}-\gamma^{\sigma}(-\gamma^{\nu}\gamma^{\rho}+\{\gamma^{\nu},\gamma^{\rho}\})\gamma^{\mu})\\ &= -\frac{1}{4}(\gamma^{\nu}\gamma^{\mu}\gamma^{\sigma}\gamma^{\rho} + \gamma^{\sigma}\gamma^{\nu}\gamma^{\rho}\gamma^{\mu} - 2g^{\nu\rho}\gamma^{\sigma}\gamma^{\mu})\\ &\cdots\\ &= -\frac{1}{4}(-2g^{\rho\nu}\gamma^{\sigma}\gamma^{\mu} + 2g^{\sigma\nu}\gamma^{\rho}\gamma^{\mu} - 2g^{\mu\rho}\gamma^{\nu}\gamma^{\sigma} + 2g^{\mu\sigma}\gamma^{\nu}\gamma^{\rho})\\ &= -\frac{1}{4}(-g^{\rho\nu}(2g^{\sigma\mu} + [\gamma^{\sigma},\gamma^{\mu}]) + g^{\sigma\nu}(2g^{\rho\mu}+[\gamma^{\rho},\gamma^{\mu}])\\ &\quad\qquad - g^{\mu\rho}(2g^{\nu\sigma}+[\gamma^{\nu},\gamma^{\sigma}]) + g^{\mu\sigma}(2g^{\mu\rho} + [\gamma^{\nu},\gamma^{\rho}])\\ &= i(g^{\nu\rho}S^{\mu\sigma}-g^{\mu\rho}S^{\nu\sigma}-g^{\nu\sigma}S^{\mu\rho}+g^{\mu\sigma}S^{\nu\rho}) \end{aligned}$

那么如何找到 Dirac 矩阵呢。不难得到，Dirac 矩阵的最低维数为 $4$ ，现在我们就针对 $4$ 维的情况下讨论，我们可以通过泡利矩阵构造 Dirac 矩阵，在 Wely 表象下有：

$\gamma^0 = \begin{pmatrix} 0 & I\\ I & 0\\ \end{pmatrix},\quad \gamma^i = \begin{pmatrix} 0 & \sigma^i\\ -\sigma^i & 0\\ \end{pmatrix}\tag{22}$

得到生成元为：

boost 生成元

$S^{0i} = \frac{i}{4}[\gamma^0,\gamma^i] = -\frac{i}{2}\begin{pmatrix} \sigma^i & 0\\ 0 & -\sigma^i\\ \end{pmatrix}\tag{22}$

rotation 生成元

$S^{ij} = \frac{i}{4}[\gamma^i,\gamma^j] = \frac{1}{2}\epsilon^{ijk}\begin{pmatrix} \sigma^k & 0\\ 0 & \sigma^k\\ \end{pmatrix}\equiv \frac{1}{2}\epsilon^{ijk} \Sigma^k \tag{23}$

我们此时可以写出 $n=4$ 的 multiplet $\psi$ ，将遵从以下变换规则：

$\psi \rightarrow \exp (-\frac{i}{2}\omega_{\mu\nu}S^{\mu\nu})\psi$

我们引入以下符号：

$\Lambda_{\frac{1}{2}} \equiv \exp (-\frac{i}{2}\omega_{\mu\nu}S^{\mu\nu}) \tag{24}$

特殊的，Dirac 矩阵 $\gamma^{\mu}$ 同时具有洛伦兹指标与旋量指标（对应 multiplet 结构）。在洛伦兹变换下，洛伦兹指标与旋量指标应当同时改变；而我们又清楚 $\gamma^{\mu}$ 只是一个常数矩阵它不应当在洛伦兹变换下改变，这件事情告诉我们：

$\Lambda^{\mu}_{\ \ \nu}\Lambda_{\frac{1}{2}}\gamma^{\nu}\Lambda^{-1}_{\frac{1}{2}} = \gamma^{\mu} \tag{25}$

这件事情的证明是容易的：只需要注意到如下对易关系：

$\begin{aligned} [S^{\rho\sigma},\gamma^{\mu}] &= \frac{i}{4}[[\gamma^{\rho},\gamma^{\sigma}],\gamma^{\mu}]\\ &= \frac{i}{4}[2g^{\rho\sigma} - 2\gamma^{\sigma}\gamma^{\rho},\gamma^{\mu}]\\ &= -\frac{i}{2}[\gamma^{\sigma}\gamma^{\rho},\gamma^{\mu}]\\ & = -\frac{i}{2}(\gamma^{\sigma}\gamma^{\rho}\gamma^{\mu}-\gamma^{\mu}\gamma^{\sigma}\gamma^{\rho})\\ &= -\frac{i}{2}(\gamma^{\sigma}\gamma^{\rho}\gamma^{\mu}+ \gamma^{\sigma}\gamma^{\mu}\gamma^{\rho} - 2g^{\mu\sigma}\gamma^{\rho})\\ &= -i(g^{\mu\rho}\gamma^{\sigma} - g^{\mu\sigma}\gamma^{\rho})\\ &= -i(g^{\mu\rho}\delta^{\sigma}_{\ \ \nu}-g^{\mu\sigma}\delta^{\rho}_{\ \ \nu})\gamma^{\nu} = -(\mathcal{J}^{\rho\sigma})^{\mu}_{\ \ \nu}\gamma^{\nu} \end{aligned}$

那么容易得到下列无穷小洛伦兹变换对应的表达式成立：

$(1 + \frac{i}{2}\omega_{\rho\sigma}S^{\rho\sigma})\gamma^{\mu}(1 - \frac{i}{2}\omega_{\rho\sigma}S^{\rho\sigma}) = (1-\frac{i}{2}\omega_{\rho\sigma}J^{\rho\sigma})^{\mu}_{\ \ \nu}\gamma^{\nu}$

即有：

$\Lambda_{\frac{1}{2}}^{-1}\gamma^{\mu}\Lambda_{\frac{1}{2}} = \Lambda^{\mu}_{\ \ \nu}\gamma^{\nu} \tag{26}$

$(26)(25)$ 两式是等价的。

如何理解对 $\gamma^{\mu}$ 旋量指标的变换是： $\Lambda_{\frac{1}{2}}\gamma^{\mu}\Lambda^{-1} _ {\frac{1}{2}}$ 呢？这是因为 $\gamma^{\nu}$ 是一个 $n\times n$ 矩阵，具有两个旋量指标，不仅需要 $\Lambda_{\frac{1}{2}}$ 放在前面对第一个旋量指标作用，还需要将 $\Lambda^{-1}_{\frac{1}{2}}$ 放在后面对第二个旋量指标作用。

Dirac 方程的洛伦兹不变性

如果一个方程的形式在洛伦兹变换下并不发生变化，那么我们称这个方程是洛伦兹不变的。例如 Klein-Gordon 方程：

$\begin{aligned} (\partial^2+m^2)\phi(x) &\rightarrow (g^{\mu\nu}\Lambda_{\mu}^{\ \ \rho}\Lambda_{\nu}^{\ \ \sigma}\partial_{\rho}\partial_{\sigma} + m^2)\phi(\Lambda^{-1}x)\\ &= (g^{\rho\sigma}\partial_{\rho}\partial_{\sigma} + m^2)\phi(\Lambda^{-1}x)\\ &= (\partial^2+m^2)\phi(\Lambda^{-1}x)\\ \end{aligned}$

变换后的方程为：

$(\partial^2+m^2)\phi(\Lambda^{-1}x) = 0$

其形式并没有发生变化。

我们可以想到，若一个体系的拉格朗日量是 洛伦兹标量 Lorentz scalar（即遵从标量场的变换规则），那么对应的运动方程自然是洛伦兹不变的方程。

现在，我们遵从 Dirac 的想法，利用 $\partial_{\mu},\gamma^{\mu},m,\psi$ 去构造一个一阶的洛伦兹不变的方程，且能够导出 Klein-Gordon 方程。满足这些条件的方程就是 Dirac 方程，如下：

$(i\gamma^{\mu}\partial_{\mu} - m)\psi = 0 \tag{27}$

这个方程和我们之前提到的方程 $(10)$ 本质上是一样的，只需要将 $(10)$ 式两边同时乘以 $\beta$ ，就能得到：

$\gamma^0 = \beta,\quad \gamma^i = \beta\alpha_i$

这件事情需要在同一个表象下进行，不过在本篇中，第一种推导采用的是 Pauli-Dirac 表象，第二种推导采用的是 Wely 表象，不能直接验证上式。

满足方程 $(27)$ 的 旋量场 spinor field $\psi(x)$ 称为 Dirac 场 Dirac field。我们对 $(27)$ 的洛伦兹不变性进行验证：

$\begin{aligned} (i\gamma^{\mu}\partial_{\mu} - m)\psi(x) &\rightarrow (i\gamma^{\mu}\Lambda_{\mu}^{\ \ \nu}\partial_{\nu} - m)\Lambda_{\frac{1}{2}}\psi(\Lambda^{-1}x)\\ & = \Lambda_{\frac{1}{2}}(i\Lambda^{-1}_{\frac{1}{2}}\gamma^{\mu}\Lambda_{\frac{1}{2}}\Lambda_{\mu}^{\ \ \nu}\partial_{\nu} - m)\psi(\Lambda^{-1}x)\\ & = \Lambda_{\frac{1}{2}}(i\gamma^{\mu}\partial_{\mu} - m)\psi(\Lambda^{-1}x) \end{aligned}\tag{28}$

即变换后的 Dirac 方程为：

$\Lambda_{\frac{1}{2}}(i\gamma^{\mu}\partial_{\mu} - m)\psi(\Lambda^{-1}x) = 0$

形式并无变化。

$(28)$ 式的推导中用到了 $(25)$ 式。在推导中需要始终明确：哪个代表矩阵分量（如 $\Lambda_{\mu}^{\ \ \nu}$ ），哪个代表矩阵（如 $\Lambda_{\frac{1}{2}}$ ），这样才能明确哪些项可以相互交换顺序，哪些则不可以。

将算子 $-i\gamma^{\mu}\partial_{\mu}-m$ 作用到方程 $(27)$ 上就能得到 Klein-Gordon 方程，这很简单。

我们现在想要得到 Dirac 方程对应的拉格朗日量（这是一个洛伦兹标量）。我们做一些尝试：

$\psi^\dagger\psi \rightarrow \psi^\dagger\Lambda^{\dagger}_{\frac{1}{2}}\Lambda_{\frac{1}{2}}\psi$

但是 $\Lambda_{\frac{1}{2}}$ 并不是幺正矩阵故 $\psi^\dagger\psi$ 不是洛伦兹标量。

我们具体考虑生成元矩阵 $S^{\mu\nu}$ ，不难得到其中 rotation 生成元 $S^{ij}$ 是厄密的，而 boost 生成元 $S^{0i}$ 是反厄密的。而考虑 $\gamma^0$ 与 rotation 生成元是对易的， $\gamma^0$ 与 boost 生成元是反对易的。综合考虑以上两点，得到:

$S^{\mu\nu\dagger}\gamma^0 = \gamma^0 S^{\mu\nu}$

故：

$\begin{aligned} \Lambda^\dagger_{\frac{1}{2}}\gamma^0 &=\exp(\frac{i}{2}\omega_{\mu\nu}S^{\mu\nu\dagger}) \gamma^0\\ &= \gamma^0\exp(\frac{i}{2}\omega_{\mu\nu}S^{\mu\nu}) \\ &= \gamma^0\Lambda_{\frac{1}{2}}^{-1}\\ \end{aligned}\tag{29}$