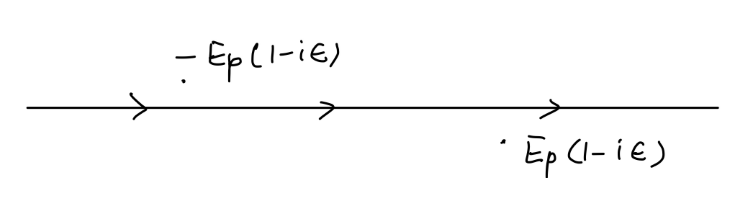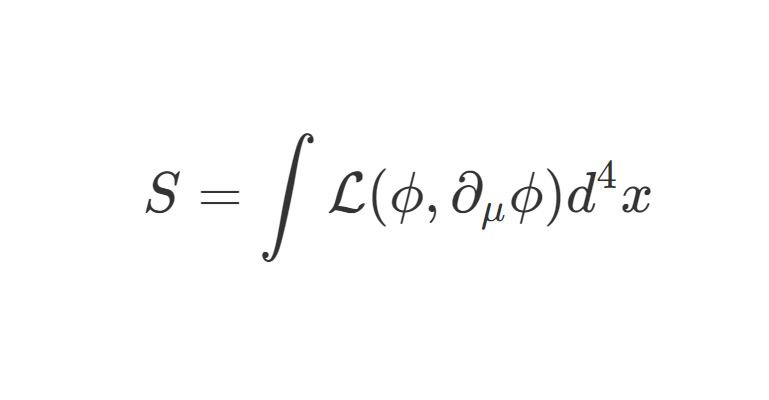Dirac 场是满足 Dirac 方程的旋量场 ψ(x)\psi(x)。现在我们尝试将 Dirac 场量子化。

我们从自由 Dirac 场的拉格朗日量出发：

L=ψˉ(i∂−m)ψ(1)\mathcal{L} = \bar{\psi}(i\cancel{\partial} - m)\psi \tag{1}

正则动量为：

π=∂L∂ψ˙=ψˉiγ0=iψ†(2)\pi = \frac{\partial \mathcal{L}}{\partial \dot{\psi}} = \bar{\psi}i\gamma^0 = i\psi^\dagger \tag{2}

于是哈密顿量可以写为：

H=∫d3xψˉ(−iγ⋅∇+m)ψ=∫d3xψ†(−iγ0γ⋅∇+γ0m)ψ(3)\begin{aligned} H &= \int d^3x\bar{\psi}(-i\bm{\gamma}\cdot\nabla+m)\psi\\ &= \int d^3x \psi^\dagger(-i\gamma^0\bm{\gamma}\cdot\nabla+\gamma^0m)\psi \end{aligned}\tag{3}

Dirac 场的量子化

对 Dirac 场进行量子化的尝试

我们尝试仿照对 Klein-Gordon 场量子化的方法对 Dirac 场进行量子化。我们先在薛定谔绘景下讨论：对于 Dirac 场，其平面波解在上一篇中已经找到：

us(p)eip⋅xvs(p)e−ip⋅xs=1,2u^s(\bm{p})e^{i\bm{p}\cdot\bm{x}}\quad v^s(\bm{p})e^{-i\bm{p}\cdot\bm{x}}\quad s= 1,2

或者写为：

us(p)eip⋅xvs(−p)eip⋅xs=1,2u^s(\bm{p})e^{i\bm{p}\cdot\bm{x}}\quad v^s(-\bm{p})e^{i\bm{p}\cdot\bm{x}}\quad s= 1,2

我们同样在动量表象中写出：

ψ(x)=∫d3p(2π)3eip⋅xψ(p)\psi(\bm{x}) = \int \frac{d^3p}{(2\pi)^3}e^{i\bm{p}\cdot\bm{x}}\psi(\bm{p})

那么 ψ(p)\psi(\bm{p}) 应当是 us(p)u^s(\bm{p}) 与 vs(−p)v^s(-\bm{p}) 的线性组合。考虑到 ψ\psi 为复值场，我们需要使用两套阶梯算子，于是得到：

ψ(p)=∑s=1,2(a^psus(p)+b^−psvs(−p))\psi(\bm{p}) = \sum_{s=1,2}(\hat{a}_{\bm{p}}^su^s(\bm{p}) + \hat{b}_{-\bm{p}}^sv^s(-\bm{p}))

那么：

ψ(x)=∫d3p(2π)312Epeip⋅x∑s=1,2(apsus(p)+b−psvs(−p))(4)\psi(\bm{x}) = \int \frac{d^3p}{(2\pi)^3}\frac{1}{\sqrt{2E_{\bm{p}}}}e^{i\bm{p}\cdot\bm{x}}\sum_{s=1,2}(a_{\bm{p}}^su^s(\bm{p}) + b_{-\bm{p}}^sv^s(-\bm{p})) \tag{4}

类似有：

ψ†(x)=∫d3p(2π)312Epe−ip⋅xγ0∑s=1,2(aps†uˉs(p)+b−ps†vˉs(−p))(5)\psi^\dagger(\bm{x}) = \int \frac{d^3p}{(2\pi)^3}\frac{1}{\sqrt{2E_{\bm{p}}}}e^{-i\bm{p}\cdot\bm{x}}\gamma^0\sum_{s=1,2}(a_{\bm{p}}^{s\dagger}\bar{u}^s(\bm{p}) + b_{-\bm{p}}^{s\dagger}\bar{v}^s(-\bm{p})) \tag{5}

现在我们需要确定一个对易关系进行量子化。我们尝试考虑：假设 aps,bpsa_{\bm{p}}^s,b_{\bm{p}}^s 满足如下对易关系，在 Klein-Gordon 场中我们正是这么做的：

[apr,aqs†]=[bpr,bqs†]=(2π)3δ(3)(p−q)δrs(6)[a_{\bm{p}}^r,a_{\bm{q}}^{s\dagger}]=[b_{\bm{p}}^r,b_{\bm{q}}^{s\dagger}] = (2\pi)^3\delta^{(3)}(\bm{p}-\bm{q})\delta^{rs} \tag{6}

则能验证 ψ(x)\psi(\bm{x}) 具有如下对易关系：

[ψ(x),ψ†(y)]=∫d3pd3q(2π)612Ep2Eqei(p⋅x−q⋅y)×∑r,s=1,2([apr,aqs†]ur(p)uˉs(q)+[b−pr,b−qs†]vr(−p)vˉs(−q))γ0=∫d3p(2π)312Epeip⋅(x−y)∑s(us(p)uˉs(p)+vs(−p)vˉs(−p))γ0=∫d3p(2π)312Epeip⋅(x−y)[(γ0Ep−γ⋅p+m)+(γ0Ep+γ⋅p−m)]γ0=∫d3p(2π)3eip⋅(x−y)=δ(3)(x−y)×14×4\begin{aligned} [\psi(\bm{x}),\psi^\dagger(\bm{y})] &= \int \frac{d^3pd^3q}{(2\pi)^6}\frac{1}{\sqrt{2E_{\bm{p}}2E_{\bm{q}}}}e^{i(\bm{p}\cdot\bm{x}-\bm{q}\cdot\bm{y})}\\ &\quad \times\sum_{r,s=1,2}([a_{\bm{p}}^r,a_{\bm{q}}^{s\dagger}]u^r(\bm{p})\bar{u}^s(\bm{q}) + [b_{-\bm{p}}^r,b_{-\bm{q}}^{s\dagger}]v^r(-\bm{p})\bar{v}^s(-\bm{q}))\gamma^0\\ &= \int \frac{d^3p}{(2\pi)^3}\frac{1}{2E_{\bm{p}}}e^{i\bm{p}\cdot(\bm{x}-\bm{y})}\sum_s (u^s(\bm{p})\bar{u}^s(\bm{p})+v^s(\bm{-p})\bar{v}^s(\bm{-p})) \gamma^0\\ &= \int \frac{d^3p}{(2\pi)^3}\frac{1}{2E_{\bm{p}}}e^{i\bm{p}\cdot(\bm{x}-\bm{y})}[(\gamma^0E_{\bm{p}} - \bm{\gamma}\cdot\bm{p} + m)+(\gamma^0E_{\bm{p}} + \bm{\gamma}\cdot\bm{p} - m)]\gamma^0\\ &= \int \frac{d^3p}{(2\pi)^3}e^{i\bm{p}\cdot(\bm{x}-\bm{y})} = \delta^{(3)}(\bm{x}-\bm{y})\times 1_{4\times4} \end{aligned}

这个结果也符合我们的预期。

上述推导中用到了 spin sum completeness relations:

∑us(p)uˉs(p)=γ⋅p−m∑vs(p)vˉs(p)=γ⋅p+m\begin{aligned} \sum u^s(p)\bar{u}^s(p) = \gamma\cdot p - m\\ \sum v^s(p)\bar{v}^s(p) = \gamma\cdot p + m\\ \end{aligned}

这样，我们继续将哈密顿量对角化。可以得到：

H=∫d3xψ†(−iγ0γ⋅∇+γ0m)ψ=∫d3x∫d3pd3q(2π)6ei(q−p)⋅x4EpEq∑rs(apr†uˉr(p)+b−pr†vˉr(−p))γ0(γ0γ⋅q+γ0m)(a^qsus(q)+b^−qsvs(−q))=∫d3x∫d3pd3q(2π)6ei(q−p)⋅x4EpEq∑rs(apr†uˉr(p)+b−pr†vˉr(−p))(γ⋅q+m)(a^qsus(q)+b^−qsvs(−q))=∫d3p(2π)312Ep∑rs(apr†uˉr(p)+b−pr†vˉr(−p))(γ⋅p+m)(a^psus(p)+b^−psvs(−p))\begin{aligned} H &= \int d^3x \psi^\dagger (-i\gamma^0\bm{\gamma}\cdot\nabla + \gamma^0 m)\psi\\ &= \int d^3x\int \frac{d^3pd^3q}{(2\pi)^6}\frac{e^{i(\bm{q}-\bm{p})\cdot\bm{x}}}{\sqrt{4E_{\bm{p}}E_{\bm{q}}}}\sum_{rs}(a_{\bm{p}}^{r\dagger}\bar{u}^r(\bm{p}) + b_{-\bm{p}}^{r\dagger}\bar{v}^r(-\bm{p}))\gamma^0\\ &\qquad (\gamma^0\bm{\gamma}\cdot\bm{q} + \gamma^0 m)(\hat{a}_{\bm{q}}^su^s(\bm{q}) + \hat{b}_{-\bm{q}}^sv^s(-\bm{q}))\\ &= \int d^3x\int \frac{d^3pd^3q}{(2\pi)^6}\frac{e^{i(\bm{q}-\bm{p})\cdot\bm{x}}}{\sqrt{4E_{\bm{p}}E_{\bm{q}}}}\sum_{rs}(a_{\bm{p}}^{r\dagger}\bar{u}^r(\bm{p}) + b_{-\bm{p}}^{r\dagger}\bar{v}^r(-\bm{p}))\\ &\qquad (\bm{\gamma}\cdot\bm{q} + m)(\hat{a}_{\bm{q}}^su^s(\bm{q}) + \hat{b}_{-\bm{q}}^sv^s(-\bm{q}))\\ &= \int \frac{d^3p}{(2\pi)^3}\frac{1}{2E_{\bm{p}}}\sum_{rs}(a_{\bm{p}}^{r\dagger}\bar{u}^r(\bm{p}) + b_{-\bm{p}}^{r\dagger}\bar{v}^r(-\bm{p}))(\bm{\gamma}\cdot\bm{p} + m)(\hat{a}_{\bm{p}}^su^s(\bm{p}) + \hat{b}_{-\bm{p}}^sv^s(-\bm{p}))\\ \end{aligned}

利用：

uˉs(p)(γ⋅p)us(p)=(ξs†p⋅σˉξs†p⋅σ)(0σ⋅p−σ⋅p0)(p⋅σξsp⋅σˉξs)=−ξs†p⋅σσ⋅pp⋅σξs+ξs†p⋅σˉσ⋅pp⋅σˉξs=−(E−p⋅σ)p⋅σ+(E+p⋅σ)p⋅σ=2p2\begin{aligned} \bar{u}^s(\bm{p})(\bm{\gamma}\cdot\bm{p})u^s(\bm{p}) &= \begin{pmatrix} \xi^{s\dagger}\sqrt{p\cdot\bar{\sigma}} & \xi^{s\dagger}\sqrt{p\cdot\sigma} \end{pmatrix}\begin{pmatrix} 0 & \bm{\sigma}\cdot\bm{p}\\ -\bm{\sigma}\cdot\bm{p} & 0\\ \end{pmatrix}\begin{pmatrix} \sqrt{p\cdot\sigma}\xi^{s}\\ \sqrt{p\cdot\bar{\sigma}}\xi^{s}\\ \end{pmatrix}\\ &= -\xi^{s\dagger}\sqrt{p\cdot\sigma}\bm{\sigma}\cdot\bm{p} \sqrt{p\cdot\sigma} \xi^s + \xi^{s\dagger}\sqrt{p\cdot\bar{\sigma}}\bm{\sigma}\cdot\bm{p} \sqrt{p\cdot\bar{\sigma}} \xi^s\\ &= -(E-\bm{p}\cdot\bm{\sigma})\bm{p}\cdot\bm{\sigma} + (E+\bm{p}\cdot\bm{\sigma})\bm{p}\cdot\bm{\sigma}\\ &= 2\bm{p}^2\\ \end{aligned}

可得

H=∫d3p(2π)3∑s(Epaps†aps−Epbps†bps)(7)\begin{aligned} H = \int \frac{d^3p}{(2\pi)^3}\sum_s(E_{\bm{p}}a^{s\dagger}_{\bm{p}}a^{s}_{\bm{p}}-E_{\bm{p}}b^{s\dagger}_{\bm{p}}b^{s}_{\bm{p}})\\ \end{aligned}\tag{7}

在这里我们发现：使用 bp†b^\dagger_{\bm{p}} 激发更多粒子后，体系的能量反而会下降，那么并不存在一个能量下限。这说明我们这里的量子化是存在一些问题的。我们这里先不作修正，继续在这个基础上进行讨论。

Dirac 场与因果律

我们现在转换到海森堡绘景下讨论 Dirac 场的传播子。

在海森堡绘景中，有：

eiHtapse−iHt=apse−iEpteiHtbpse−iHt=bpseiEpte^{iHt}a_{\bm{p}}^se^{-iHt} = a_{\bm{p}}^se^{-iE_{\bm{p}}t}\quad e^{iHt}b_{\bm{p}}^se^{-iHt} = b_{\bm{p}}^se^{iE_{\bm{p}}t}

根据 (4)(5)(4)(5)，立即得到在海森堡绘景中 ψ,ψˉ\psi,\bar{\psi} 的表达式：

ψ(x)=∫d3p(2π)312Ep∑s=1,2(apsus(p)e−ip⋅x+bpsvs(p)eip⋅x)ψˉ(x)=∫d3p(2π)312Ep∑s=1,2(aps†uˉs(p)eip⋅x+bps†vˉs(p)e−ip⋅x)\begin{aligned} \psi(x) &= \int \frac{d^3p}{(2\pi)^3}\frac{1}{\sqrt{2E_{\bm{p}}}}\sum_{s=1,2}(a_{\bm{p}}^su^s(\bm{p})e^{-ip\cdot x} + b_{\bm{p}}^sv^s(\bm{p})e^{ip\cdot x})\\ \bar{\psi}(x) &= \int \frac{d^3p}{(2\pi)^3}\frac{1}{\sqrt{2E_{\bm{p}}}}\sum_{s=1,2}(a_{\bm{p}}^{s\dagger}\bar{u}^s(\bm{p})e^{ip \cdot x} + b_{\bm{p}}^{s\dagger}\bar{v}^s(\bm{p})e^{-ip\cdot x})\\ \end{aligned}

为了讨论因果律，我们需要计算如下对易子：

[ψa(x),ψˉb(y)]=∫d3p(2π)312Ep∑s(uas(p)uˉbs(p)e−ip⋅(x−y)+vas(p)vˉbs(p)eip⋅(x−y))=∫d3p(2π)312Ep((γ⋅p+m)abe−ip⋅(x−y)+(γ⋅p−m)abeip⋅(x−y))=(iγ⋅∂x+m)ab∫d3p(2π)312Ep(e−ip⋅(x−y)−eip⋅(x−y))=(iγ⋅∂x+m)ab[ϕ(x),ϕ(y)]\begin{aligned} [\psi_a(x),\bar{\psi}_b(y)] &= \int \frac{d^3p}{(2\pi)^3}\frac{1}{2E_{\bm{p}}}\sum_{s}(u^s_a(\bm{p})\bar{u}^s_b(\bm{p})e^{-ip\cdot(x-y)}+v^s_a(\bm{p})\bar{v}^s_b(\bm{p})e^{ip\cdot(x-y)})\\ &=\int \frac{d^3p}{(2\pi)^3}\frac{1}{2E_{\bm{p}}}((\gamma\cdot p + m)_{ab}e^{-ip\cdot(x-y)}+(\gamma\cdot p - m)_{ab}e^{ip\cdot(x-y)})\\ &= (i\gamma\cdot\partial_x + m)_{ab}\int \frac{d^3p}{(2\pi)^3}\frac{1}{2E_{\bm{p}}}(e^{-ip\cdot(x-y)}-e^{ip\cdot(x-y)})\\ &= (i\gamma\cdot\partial_x + m)_{ab} [\phi(x),\phi(y)] \end{aligned}

我们发现，最后实际上会得到 Klein-Gordon 传播子。我们之前讨论过：Klein-Gordon 传播子对于类空间隔为零，这意味着 Dirac 传播子也具有同样的性质。

回忆 Klein-Grodon Propagator 的物理意义：

[ϕ(x),ϕ(y)]=D(x−y)−D(y−x)[\phi(x),\phi(y)] = D(x-y)-D(y-x)

分别表示：正粒子从 y\bm{y} 传播 x\bm{x} 的概率幅与反粒子从 x\bm{x} 传播 y\bm{y} 的概率幅的叠加。

对于以上得到的 Dirac 传播子来说，它可以表示为：

[ψa(x),ψˉb(y)]=⟨0∣[ψa(x),ψˉb(y)]∣0⟩=⟨0∣ψa(x)ψˉb(x)∣0⟩−⟨0∣ψˉb(x)ψa(x)∣0⟩\begin{aligned} [\psi_a(x),\bar{\psi}_b(y)] &= \langle 0 | [\psi_a(x),\bar{\psi}_b(y)] |0\rangle \\ &= \langle 0| \psi_a(x)\bar{\psi}_b(x)|0\rangle - \langle 0| \bar{\psi}_b(x)\psi_a(x)|0\rangle \end{aligned}

考虑到任意正/反粒子产生算子 a^ps,b^ps\hat{a}_{\bm{p}}^s,\hat{b}_{\bm{p}}^s 作用于真空态 ∣0⟩|0\rangle 应当有：

a^ps∣0⟩=b^ps∣0⟩=0\hat{a}_{\bm{p}}^s|0\rangle = \hat{b}_{\bm{p}}^s|0\rangle = 0

如此 Dirac 传播子的第二项为零。Dirac 传播子将只剩下正粒子从 x\bm{x} 传播到 y\bm{y} 的项。这是我们所不希望看到的，现在我们希望 Dirac传播子中也包含有关反粒子的传播项。结合之前有关体系能量下限的讨论：我们这里对 Dirac 场的量子化不正确的。这意味着：量子化条件 (6)(6) 是不合适的。现在我们以 Dirac 传播子应当包含正/反粒子的传播项作为一个基本的出发点，对 Dirac 场进行量子化。

Dirac 场的量子化

首先考虑 ⟨0∣ψ(x)ψˉ(y)∣0⟩\langle 0 |\psi(x)\bar{\psi}(y)|0\rangle 应当对应正粒子从 yy 到 xx 的传播。所以：ψˉ(y)∣0⟩\bar{\psi}(y)|0\rangle 与 ⟨0∣ψ(x)\langle 0|\psi(x) 应当只包含正粒子项。这意味着 ψˉ(y)∣0⟩\bar{\psi}(y)|0\rangle 应当只包含 aps†a^{s\dagger}_{\bm{p}}；同理，⟨0∣ψ(x)\langle 0|\psi(x) 只包含 apsa_{\bm{p}}^s。因此，我们得到 ⟨0∣ψ(x)ψˉ(y)∣0⟩\langle 0|\psi(x)\bar{\psi}(y)|0\rangle 的形式应当为如下：

⟨0∣ψ(x)ψˉ(y)∣0⟩=⟨0∣∫d3p(2π)312Ep∑raprur(p)e−ipx×∫d3p(2π)312Eq∑saqs†us(q)eiqy∣0⟩\begin{aligned} \langle 0|\psi(x)\bar{\psi}(y)|0\rangle &= \langle 0|\int \frac{d^3p}{(2\pi)^3}\frac{1}{\sqrt{2E_{\bm{p}}}} \sum_r a_{\bm{p}}^r u^r(\bm{p})e^{-ipx}\\ &\quad \times \int \frac{d^3p}{(2\pi)^3}\frac{1}{\sqrt{2E_{\bm{q}}}} \sum_s a_{\bm{q}}^{s\dagger} u^s(\bm{q})e^{iqy}|0\rangle\\ \end{aligned}

矩阵元 ⟨0∣apraqs†∣0⟩\langle 0|a_{\bm{p}}^ra_{\bm{q}}^{s\dagger}|0\rangle 的形式应当如下：

⟨0∣apraqs†∣0⟩=(2π)3δ(3)(p−q)δrs⋅A(p)\langle 0|a_{\bm{p}}^ra_{\bm{q}}^{s\dagger}|0\rangle = (2\pi)^3 \delta^{(3)}(\bm{p}-\bm{q})\delta^{rs}\cdot A(\bm{p})

如此可得：

⟨0∣ψa(x)ψˉb(y)∣0⟩=(iγ⋅∂x+m)ab∫d3p(2π)312Epe−ip(x−y)⋅A(p)(8)\langle 0|\psi_a(x)\bar{\psi}_b(y)|0\rangle = (i\gamma\cdot\partial_x+m)_{ab}\int \frac{d^3p}{(2\pi)^3}\frac{1}{2E_{\bm{p}}}e^{-ip(x-y)}\cdot A(\bm{p})\tag{8}

现在我们来考虑 A(p)A(\bm{p}) 的性质：

  1. ⟨0∣apsaps†∣0⟩=∣aps†∣0⟩∣2>0⇒A>0\langle 0| a_{\bm{p}}^s a_{\bm{p}}^{s\dagger} |0\rangle = |a^{s\dagger}_{\bm{p}}|0\rangle|^2 > 0 \Rightarrow A > 0

⟨0∣ψ(x)ψˉ(y)∣0⟩→Λ⟨0∣Λ12ψ(x)ψˉ(y)Λ12−1∣0⟩=⟨0∣ψ(x)ψˉ(y)∣0⟩\begin{aligned} \langle 0|\psi(x)\bar{\psi}(y)|0\rangle & \overset{\Lambda}{\rightarrow} \langle 0|\Lambda_{\frac{1}{2}}\psi(x)\bar{\psi}(y)\Lambda^{-1}_{\frac{1}{2}}|0\rangle\\ &= \langle 0|\psi(x)\bar{\psi}(y)|0\rangle \end{aligned}

即 (8)(8) 式为一个洛伦兹不变量，这要求 A(p)A(\bm{p}) 为一个洛伦兹标量。可得：

A(p)=A(p2)=A(m2)A(\bm{p}) = A(p^2) = A(m^2)

即 AA 为一个正常数。

同理有：

⟨0∣ψˉb(y)ψa(x)∣0⟩=−(iγ⋅∂x+m)ab∫d3p(2π)312Epeip(x−y)⋅B(9)\langle 0|\bar{\psi}_b(y)\psi_a(x)|0\rangle = -(i\gamma\cdot\partial_x+m)_{ab}\int \frac{d^3p}{(2\pi)^3}\frac{1}{2E_{\bm{p}}}e^{ip(x-y)}\cdot B \tag{9}

对于类空间隔，虽然我们不能得到 ⟨0∣[ψ(x),ψˉ(y)]∣0⟩=0\langle 0|[\psi(x),\bar{\psi}(y)]|0\rangle = 0，但是通过设定 A=B=1A=B=1，将会得到（光锥外）：

⟨0∣ψa(x)ψˉb(y)∣0⟩=−⟨0∣ψˉb(y)ψa(x)∣0⟩\langle 0|\psi_a(x)\bar{\psi}_b(y)|0\rangle = -\langle 0|\bar{\psi}_b(y)\psi_a(x)|0\rangle

这仍然能保证因果律。这是因为所有的可观测量都是由偶数个旋量场的乘积项组成。对于任意的可观测量 O1,O2\mathcal{O}_1,\mathcal{O}_2，对于类空间隔均有：

[O1,O2]=0[\mathcal{O}_1,\mathcal{O}_2] = 0

举例说明：考虑 A=ψa†ψa,B=ψb†ψb\mathcal{A} = \psi^\dagger_a\psi_a,\mathcal{B} = \psi^\dagger_b\psi_b。
那么有：

[A,B]=[ψa†ψa,ψb†ψb]=ψa†ψaψb†ψb−ψb†ψbψa†ψa=ψa†ψaψb†ψb+ψb†ψa†ψbψa=ψa†ψaψb†ψb+ψa†ψb†ψaψb=ψa†ψaψb†ψb−ψa†ψaψb†ψb=0\begin{aligned} [\mathcal{A},\mathcal{B}]&= [\psi^\dagger_a\psi_a,\psi^\dagger_b\psi_b]\\ &= \psi^\dagger_a\psi_a\psi^\dagger_b\psi_b-\psi^\dagger_b\psi_b\psi^\dagger_a\psi_a\\ &= \psi^\dagger_a\psi_a\psi^\dagger_b\psi_b+\psi^\dagger_b\psi^\dagger_a\psi_b\psi_a\\ &= \psi^\dagger_a\psi_a\psi^\dagger_b\psi_b+\psi^\dagger_a\psi^\dagger_b\psi_a\psi_b\\ &= \psi^\dagger_a\psi_a\psi^\dagger_b\psi_b-\psi^\dagger_a\psi_a\psi^\dagger_b\psi_b = 0\\ \end{aligned}

因此，关于 Dirac 传播子的讨论启发我们可以使用如下 反对易关系 作为量子化条件：

{ψa(x),ψb†(y)}=δ(3)(x−y)δab{ψa(x),ψb(y)}={ψa†(x),ψb†(y)}=0\begin{aligned} \{\psi_a(\bm{x}),\psi_b^\dagger(\bm{y})\} &= \delta^{(3)}(\bm{x}-\bm{y})\delta_{ab}\\ \{\psi_a(\bm{x}),\psi_b(\bm{y})\} &= \{\psi^\dagger_a(\bm{x}),\psi^\dagger_b(\bm{y})\} = 0\\ \end{aligned}

这等价于阶梯算子的如下反对易关系：

{apr,aqs†}={bpr,bqs†}=(2π)3δ(3)(p−q)δrs\{a_{\bm{p}}^r,a_{\bm{q}}^{s\dagger}\}=\{b_{\bm{p}}^r,b_{\bm{q}}^{s\dagger}\} = (2\pi)^3\delta^{(3)}(\bm{p}-\bm{q})\delta^{rs}

在薛定谔绘景中，将 ψ,ψˉ\psi,\bar{\psi} 用阶梯算子表示为：

ψ(x)=∫d3p(2π)312Ep∑s(apsus(p)eip⋅x+bps†vs(p)e−ip⋅x)=∫d3p(2π)312Ep∑seip⋅x(apsus(p)+b−ps†vs(−p))ψˉ(x)=∫d3p(2π)312Ep∑s(bpsvˉs(p)eip⋅x+aps†uˉs(p)e−ip⋅x)=∫d3p(2π)312Ep∑seip⋅x(bpsvˉs(p)+a−ps†uˉs(−p))\begin{aligned} \psi(\bm{x}) &= \int \frac{d^3p}{(2\pi)^3}\frac{1}{\sqrt{2E_{\bm{p}}}}\sum_s (a_{\bm{p}}^su^s(\bm{p})e^{i\bm{p}\cdot \bm{x}} + b_{\bm{p}}^{s\dagger}v^s(\bm{p})e^{-i\bm{p}\cdot \bm{x}})\\ &= \int \frac{d^3p}{(2\pi)^3}\frac{1}{\sqrt{2E_{\bm{p}}}}\sum_s e^{i\bm{p}\cdot \bm{x}}(a_{\bm{p}}^su^s(\bm{p}) + b_{-\bm{p}}^{s\dagger}v^s(-\bm{p}))\\ \bar{\psi}(\bm{x}) &= \int \frac{d^3p}{(2\pi)^3}\frac{1}{\sqrt{2E_{\bm{p}}}}\sum_s (b_{\bm{p}}^s\bar{v}^s(\bm{p})e^{i\bm{p}\cdot \bm{x}} + a_{\bm{p}}^{s\dagger}\bar{u}^s(\bm{p})e^{-i\bm{p}\cdot \bm{x}})\\ &= \int \frac{d^3p}{(2\pi)^3}\frac{1}{\sqrt{2E_{\bm{p}}}}\sum_s e^{i\bm{p}\cdot \bm{x}}(b_{\bm{p}}^s\bar{v}^s(\bm{p}) + a_{-\bm{p}}^{s\dagger}\bar{u}^s(-\bm{p}))\\ \end{aligned}

现在将哈密顿量对角化：

H=∫d3xψˉ(−iγ⋅∇+m)ψ=∫d3x∫d3pd3q(2π)6ei(p+q)⋅x4EpEq∑rs(bpsvˉs(p)+a−ps†uˉs(−p))(γ⋅q+m)(aqsus(q)+b−qs†vs(−q))=∫d3p(2π)312Ep∑rs(bpsvˉs(p)+a−ps†uˉs(−p))(−γ⋅p+m)(a−psus(−p)+bps†vs(p))=∫d3p(2π)3Ep∑s(aps†aps−bpsbps†)=∫d3p(2π)3Ep∑s(aps†aps+bps†bps)\begin{aligned} H &= \int d^3x \bar{\psi} (-i\bm{\gamma}\cdot\nabla + m)\psi\\ &= \int d^3x\int \frac{d^3pd^3q}{(2\pi)^6}\frac{e^{i(\bm{p}+\bm{q})\cdot\bm{x}}}{\sqrt{4E_{\bm{p}}E_{\bm{q}}}}\sum_{rs}(b_{\bm{p}}^s\bar{v}^s(\bm{p}) + a_{-\bm{p}}^{s\dagger}\bar{u}^s(-\bm{p}))\\ &\qquad (\bm{\gamma}\cdot\bm{q} + m)(a_{\bm{q}}^su^s(\bm{q}) + b_{-\bm{q}}^{s\dagger}v^s(-\bm{q}))\\ &= \int \frac{d^3p}{(2\pi)^3}\frac{1}{2E_{\bm{p}}}\sum_{rs}(b_{\bm{p}}^s\bar{v}^s(\bm{p}) + a_{-\bm{p}}^{s\dagger}\bar{u}^s(-\bm{p}))(-\bm{\gamma}\cdot\bm{p} + m)(a_{-\bm{p}}^su^s(-\bm{p}) + b_{\bm{p}}^{s\dagger}v^s(\bm{p}))\\ &= \int \frac{d^3p}{(2\pi)^3}E_{\bm{p}}\sum_s(a^{s\dagger}_{\bm{p}}a^{s}_{\bm{p}}-b^{s}_{\bm{p}}b^{s\dagger}_{\bm{p}})\\ &= \int \frac{d^3p}{(2\pi)^3}E_{\bm{p}}\sum_s(a^{s\dagger}_{\bm{p}}a^{s}_{\bm{p}}+b^{s\dagger}_{\bm{p}}b^{s}_{\bm{p}})\\ \end{aligned}

真空态满足：

aps∣0⟩=bps∣0⟩=0a_{\bm{p}}^s|0\rangle=b_{\bm{p}}^s|0\rangle = 0

这样我们就解决了能量本征值不存在下限的问题。

我们来考虑一组具有反对易关系算子的性质。具体来说，我们有：

{b,b}={b†,b†}=0{b,b†}=1\begin{aligned} &\{b,b\}=\{b^\dagger,b^\dagger\}=0\\ &\{b,b^\dagger\} = 1\\ \end{aligned}

真空态 ∣0⟩|0\rangle 具有性质：

b∣0⟩=0b|0\rangle = 0

我们定义 b†∣0⟩=∣1⟩b^\dagger|0\rangle = |1\rangle。那么根据阶梯算子的反对易关系。我们可以得到：

b∣1⟩=∣0⟩b†∣1⟩=0b|1\rangle = |0\rangle\quad b^\dagger|1\rangle = 0

于是，bb 与 b†b^\dagger 所作用的 Hilbert 空间实际上只有 ∣0⟩,∣1⟩|0\rangle,|1\rangle 两个态。我们定义 ∣0⟩|0\rangle 或 ∣1⟩|1\rangle 为真空态的这两种描述都是等价的。

我们发现，Dirac 场所描述粒子具有如下性质：

  • 每个态上至多填充一个粒子

(ap†)2∣0⟩=0(a_{\bm{p}}^\dagger)^2|0\rangle = 0

  • 波函数具有交换反对称性

ap†aq†∣0⟩=−aq†ap†∣0⟩a_{\bm{p}}^\dagger a_{\bm{q}}^\dagger|0\rangle = -a_{\bm{q}}^\dagger a_{\bm{p}}^\dagger|0\rangle

这符合 Fermi-Dirac 分布，我们说：Dirac 场描述自旋为 12\frac{1}{2} 的费米子。

时空中的 Dirac 场

经过以上讨论。我们再重新总结一下对 Dirac 场的量子化过程。现在我们在海森堡绘景中讨论。

我们将 ψ,ψˉ\psi,\bar{\psi} 用阶梯算子写为：

ψ(x)=∫d3p(2π)312Ep∑s(apsus(p)e−ip⋅x+bps†vs(p)eip⋅x)ψˉ(x)=∫d3p(2π)312Ep∑s(bpsvˉs(p)e−ip⋅x+aps†uˉs(p)eip⋅x)(10)\begin{aligned} \psi(x) &= \int \frac{d^3p}{(2\pi)^3}\frac{1}{\sqrt{2E_{\bm{p}}}}\sum_s (a_{\bm{p}}^s u^s(p)e^{-ip\cdot x}+b_{\bm{p}}^{s\dagger} v^s(p)e^{ip\cdot x})\\ \bar{\psi}(x) &= \int \frac{d^3p}{(2\pi)^3}\frac{1}{\sqrt{2E_{\bm{p}}}}\sum_s (b_{\bm{p}}^s \bar{v}^s(p)e^{-ip\cdot x}+a_{\bm{p}}^{s\dagger} \bar{u}^s(p)e^{ip\cdot x})\\ \end{aligned}\tag{10}

其中阶梯算子满足反对易关系：

{apr,aqs†}={bpr,bqs†}=(2π)3δ(3)(p−q)δrs(11)\{a_{\bm{p}}^r,a_{\bm{q}}^{s\dagger}\}=\{b_{\bm{p}}^r,b_{\bm{q}}^{s\dagger}\} = (2\pi)^3\delta^{(3)}(\bm{p}-\bm{q})\delta^{rs} \tag{11}

等价的，ψ,ψ†\psi,\psi^\dagger 满足等时反对易关系：

{ψa(x),ψb†(y)}=δ(3)(x−y)δab{ψa(x),ψb(y)}={ψa†(x),ψb†(y)}=0\begin{aligned} &\{\psi_a(x),\psi_b^\dagger(y)\} = \delta^{(3)}(\bm{x}-\bm{y})\delta_{ab}\\ &\{\psi_a(x),\psi_b(y)\} = \{\psi^\dagger_a(x),\psi^\dagger_b(y)\} = 0\\ \end{aligned}

定义真空态 ∣0⟩|0\rangle 满足：

a^p∣0⟩∣0⟩=b^p∣0⟩∣0⟩=0\hat{a}_{p}|0\rangle|0\rangle = \hat{b}_{p}|0\rangle|0\rangle = 0

哈密顿量和动量可以表示为：

H=∫d3p(2π)3∑sEp(aps†aps+bps†bps)P=∫d3p(2π)3∑sp(aps†aps+bps†bps)\begin{aligned} H &= \int \frac{d^3p}{(2\pi)^3}\sum_s E_{\bm{p}}(a^{s\dagger}_{\bm{p}}a^{s}_{\bm{p}}+b_{\bm{p}}^{s\dagger}b_{\bm{p}}^s) \\ \bm{P} &= \int \frac{d^3p}{(2\pi)^3}\sum_s\bm{p}(a^{s\dagger}_{\bm{p}}a^{s}_{\bm{p}}+b_{\bm{p}}^{s\dagger}b_{\bm{p}}^s) \\ \end{aligned}

利用产生算子，单粒子态可以表示为：

∣p,s⟩≡2Epa^p†∣0⟩(12)|\bm{p},s\rangle \equiv \sqrt{2E_{\bm{p}}}\hat{a}_{\bm{p}}^\dagger |0\rangle \tag{12}

如此定义得到的粒子态的内积如下：

⟨q,r∣p,s⟩=2Ep(2π)3δ(3)(p−q)δrs(13)\langle \bm{q},r|\bm{p},s\rangle = 2E_{\bm{p}}(2\pi)^3\delta^{(3)}(\bm{p}-\bm{q})\delta^{rs} \tag{13}

这是洛伦兹不变的。因此，考虑对粒子态 ∣p,s⟩|\bm{p},s\rangle 进行洛伦兹变换 Λ\Lambda 所对应的算子 U(Λ)U(\Lambda) 应当是幺正的。考虑式 (12)(12):

U(Λ)∣p,s⟩=2EpU(Λ)ap†∣0⟩=2EpU(Λ)ap†U−1(Λ)U(Λ)∣0⟩=2EpU(Λ)ap†U−1(Λ)∣0⟩(14)\begin{aligned} U(\Lambda)|\bm{p},s\rangle &= \sqrt{2E_{\bm{p}}}U(\Lambda)a_{\bm{p}}^\dagger |0\rangle\\ &= \sqrt{2E_{\bm{p}}}U(\Lambda)a_{\bm{p}}^\dagger U^{-1}(\Lambda) U(\Lambda) |0\rangle\\ &= \sqrt{2E_{\bm{p}}}U(\Lambda)a_{\bm{p}}^\dagger U^{-1}(\Lambda)|0\rangle\\ \end{aligned}\tag{14}

另一方面，有：

U(Λ)∣p,s⟩=∣Λp,s⟩=2EΛpaΛp†∣0⟩(15)\begin{aligned} U(\Lambda)|\bm{p},s\rangle &= |\Lambda\bm{p},s\rangle\\ &=\sqrt{2E_{\Lambda\bm{p}}}a_{\Lambda\bm{p}}^\dagger |0\rangle \tag{15} \end{aligned}

从 (14),(15)(14),(15) 可以得到：

U(Λ)aps†U−1(Λ)=EΛpEpaΛps†(16)U(\Lambda)a_{\bm{p}}^{s\dagger}U^{-1}(\Lambda) = \sqrt{\frac{E_{\Lambda\bm{p}}}{E_{\bm{p}}}}a^{s\dagger}_{\Lambda\bm{p}} \tag{16}

考虑对场量的洛伦兹变换：

ψ(x)→Uψ(x)U−1=U∫d3p(2π)312Ep∑s(apsus(p)e−ip⋅x+bps†vs(p)eip⋅x)U−1=p~=Λp∫d3p~(2π)312Ep~∑s(ap~sus(Λ−1p~)e−ip~⋅Λx+bp~s†vs(Λ−1p~)eip~⋅Λx)=∫d3p~(2π)312Ep~∑s(Λ12−1ap~sus(p~)e−ip~⋅Λx+Λ12−1bp~s†vs(p~)eip~⋅Λx)=Λ12−1ψ(Λx)\begin{aligned} \psi(x) &\rightarrow U\psi(x)U^{-1}\\ &= U\int \frac{d^3p}{(2\pi)^3}\frac{1}{\sqrt{2E_{\bm{p}}}}\sum_s (a_{\bm{p}}^s u^s(p)e^{-ip\cdot x}+b_{\bm{p}}^{s\dagger} v^s(p)e^{ip\cdot x})U^{-1}\\ &\overset{\tilde{p}=\Lambda p}{=}\int \frac{d^3\tilde{p}}{(2\pi)^3}\frac{1}{\sqrt{2E_{\tilde{\bm{p}}}}}\sum_s (a_{\tilde{\bm{p}}}^s u^s(\Lambda^{-1}\tilde{p})e^{-i\tilde{p}\cdot \Lambda x}+b_{\tilde{\bm{p}}}^{s\dagger} v^s(\Lambda^{-1}\tilde{p})e^{i\tilde{p}\cdot \Lambda x})\\ &=\int \frac{d^3\tilde{p}}{(2\pi)^3}\frac{1}{\sqrt{2E_{\tilde{\bm{p}}}}}\sum_s (\Lambda^{-1}_{\frac{1}{2}}a_{\tilde{\bm{p}}}^s u^s(\tilde{p})e^{-i\tilde{p}\cdot \Lambda x}+\Lambda^{-1}_{\frac{1}{2}}b_{\tilde{\bm{p}}}^{s\dagger} v^s(\tilde{p})e^{i\tilde{p}\cdot \Lambda x})\\ &= \Lambda^{-1}_{\frac{1}{2}}\psi(\Lambda x) \end{aligned}

注意：此处和我们之前讨论的对旋量场 ψ(x)\psi(x) 的进行变换的内涵是不同的，这里 ψ(x)\psi(x) 成为了由阶梯算子构成的矩阵。

在之前，我们提到对 Dirac 场相位变换对应的守恒流为：

jμ=ψˉγμψj^{\mu} = \bar{\psi}\gamma^{\mu}\psi

对应的守恒荷为：

Q=∫d3xj0=∫d3xψˉγ0ψ=∫d3x∫d3pd3q(2π)614EpEq∑rs(b^prvr†(p)+a^−ps†ur†(−p))⋅(a^qsus(q)+b^−qs†vs(−q))ei(p+q)⋅x=∫d3p(2π)312Ep∑rs(b^prvr†(p)+a^−ps†ur†(−p))(a^−psus(−p)+b^ps†vs(p))=∫d3p(2π)3∑s(b^psb^ps†+a^ps†a^ps)=∫d3p(2π)3∑s(a^ps†a^ps−b^ps†b^ps)\begin{aligned} Q &= \int d^3x j^0\\ &= \int d^3x \bar{\psi}\gamma^0\psi\\ &= \int d^3x \int \frac{d^3pd^3q}{(2\pi)^6}\frac{1}{\sqrt{4E_{\bm{p}}E_{\bm{q}}}}\sum_{rs}(\hat{b}_{\bm{p}}^r v^{r\dagger}(\bm{p}) + \hat{a}_{-\bm{p}}^{s\dagger}u^{r\dagger}(-\bm{p}))\\ &\qquad \cdot (\hat{a}_{\bm{q}}^s u^s(\bm{q}) + \hat{b}_{-\bm{q}}^{s\dagger} v^s(-\bm{q}))e^{i(\bm{p}+\bm{q})\cdot\bm{x}}\\ &= \int \frac{d^3p}{(2\pi)^3}\frac{1}{2E_{\bm{p}}}\sum_{rs}(\hat{b}_{\bm{p}}^r v^{r\dagger}(\bm{p}) + \hat{a}_{-\bm{p}}^{s\dagger}u^{r\dagger}(-\bm{p}))(\hat{a}_{-\bm{p}}^s u^s(-\bm{p}) + \hat{b}_{\bm{p}}^{s\dagger} v^s(\bm{p}))\\ &= \int \frac{d^3p}{(2\pi)^3}\sum_{s}(\hat{b}^s_{\bm{p}}\hat{b}^{s\dagger}_{\bm{p}}+ \hat{a}^{s\dagger}_{\bm{p}} \hat{a}^s_{\bm{p}})\\ &= \int \frac{d^3p}{(2\pi)^3}\sum_{s}(\hat{a}^{s\dagger}_{\bm{p}} \hat{a}^s_{\bm{p}} - \hat{b}^{s\dagger}_{\bm{p}}\hat{b}^s_{\bm{p}})\\ \end{aligned}

我们之前提到过，当 Dirac 场与电磁场耦合在一起时，QQ 就对应电荷。那么从上式可以得到：正粒子与反粒子携带的荷相反。

现在再来看 Dirac 传播子 Dirac Propagator。定义：

SRab(x−y)≡θ(x0−y0)⟨0∣{ψa(x),ψˉb(y)}∣0⟩(17)S^{ab}_R(x-y) \equiv \theta(x^0-y^0)\langle 0|\{\psi_a(x),\bar{\psi}_b(y)\}|0\rangle \tag{17}

由 (8)(9)(8)(9) 易得：

SR(x−y)=(i∂x+m)DR(x−y)(18)S_R(x-y) = (i\cancel{\partial}_x + m)D_R(x-y) \tag{18}

可得 SR(x−y)S_R(x-y) 为 Dirac 方程的推迟格林函数：

(i∂x−m)SR(x−y)=(i∂x−m)(i∂x+m)DR(x−y)=−(∂2+m2)DR(x−y)=iδ(4)(x−y)×14×4(19)\begin{aligned} (i\cancel{\partial}_x-m)S_R(x-y) &= (i\cancel{\partial}_x-m)(i\cancel{\partial}_x+m)D_R(x-y)\\ &= -(\partial^2+m^2)D_R(x-y)\\ &= i\delta^{(4)}(x-y)\times \bm{1}_{4\times 4} \end{aligned}\tag{19}

将：

SR(x−y)=∫d4p(2π)4e−ip⋅(x−y)S~R(p)S_R(x-y) = \int \frac{d^4p}{(2\pi)^4}e^{-ip\cdot(x-y)}\tilde{S}_R(p)

代入得：

S~R=ip−m=i(p+m)p2−m2(20)\tilde{S}_R = \frac{i}{\cancel{p}-m} = \frac{i(\cancel{p}+m)}{p^2-m^2} \tag{20}

可得：

SR=∫d4p(2π)4i(p+m)p2−m2e−ip⋅(x−y)S_R = \int \frac{d^4p}{(2\pi)^4}\frac{i(\cancel{p}+m)}{p^2-m^2}e^{-ip\cdot(x-y)}

这当然是选取了以下的 p0p^0 围线。

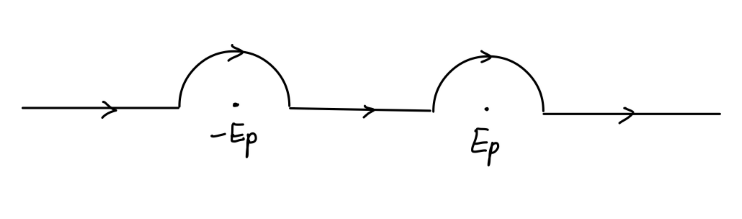
类似在 Klein-Gordon 传播子中的方法，我们使极点稍偏离实轴，再取积分路径为实轴。

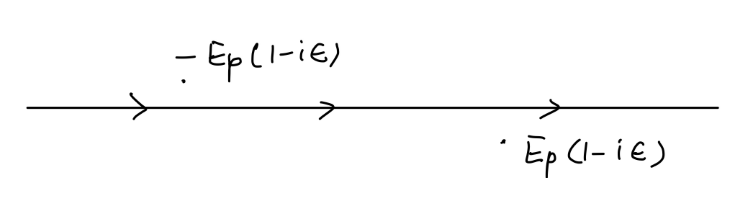
得到：

SF(x−y)=∫d4p(2π)4i(p+m)p2−m2e−ip⋅(x−y)={⟨0∣ψ(x)ψˉ(y)∣0⟩x0>y0−⟨0∣ψˉ(y)ψ(x)∣0⟩x0<y0=⟨0∣Tψ(x)ψˉ(y)∣0⟩(21)\begin{aligned} S_F(x-y) &= \int \frac{d^4p}{(2\pi)^4}\frac{i(\cancel{p}+m)}{p^2-m^2}e^{-ip\cdot(x-y)}\\ &= \left\{ \begin{aligned} \langle 0|\psi(x)\bar{\psi}(y)|0\rangle \quad x^0>y^0\\ -\langle 0|\bar{\psi}(y)\psi(x)|0\rangle \quad x^0<y^0\\ \end{aligned} \right.\\ &= \langle 0|T\psi(x)\bar{\psi}(y)|0\rangle \end{aligned}\tag{21}

可以验证，SFS_F 为 Dirac 方程的格林函数。