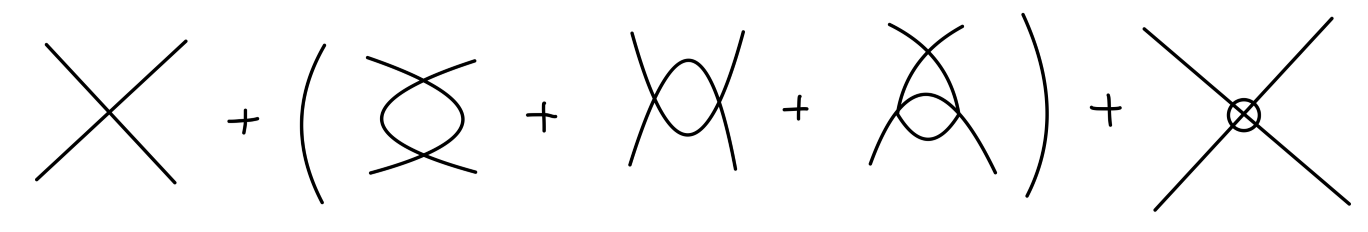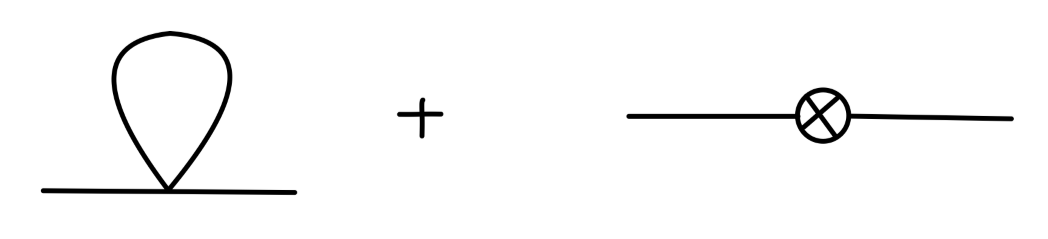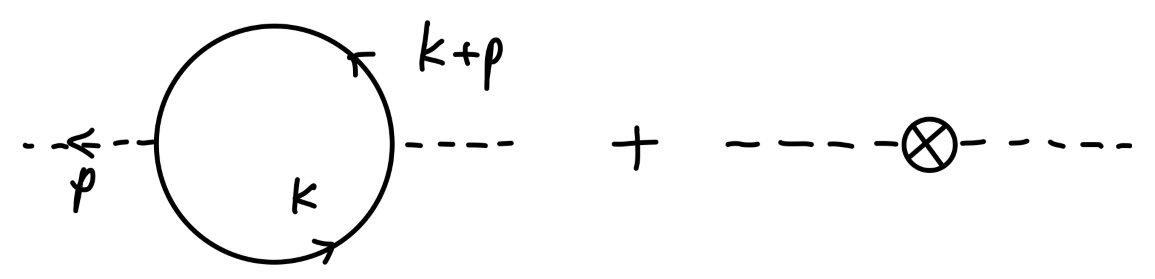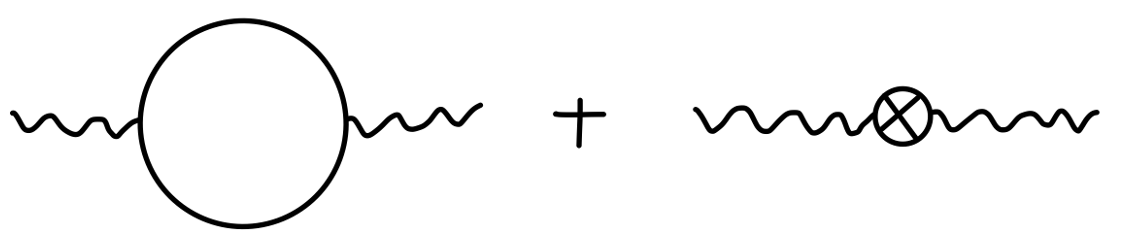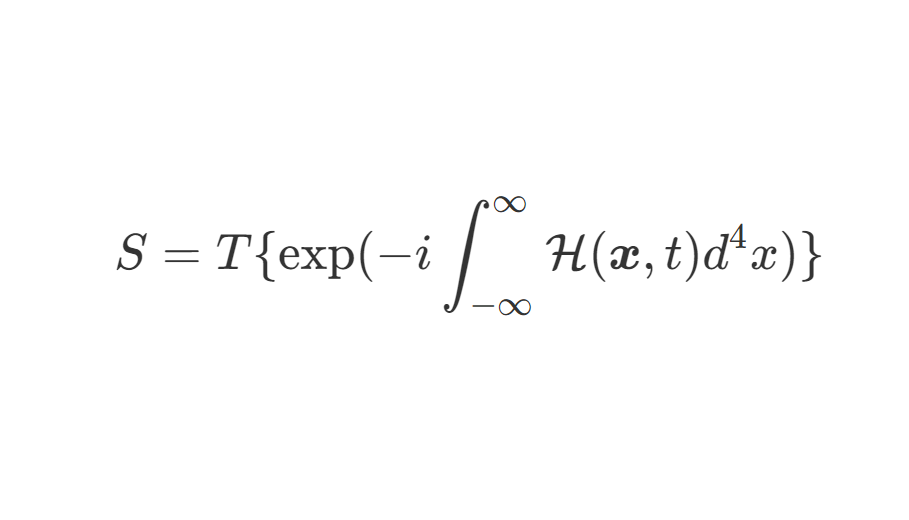重整化微扰论
对于包含发散的图,我们为了得到有限的结果,将遵从以下步骤进行处理:
-
引入正规化方法,得到一个依赖于裸参数 m0,e0 以及截断 Λ 的值。
-
计算物理质量 m 与物理电荷量 e。若想要计算散射矩阵,还需要计算场强重整化常数 Z。
-
将这些表达式结合起来,用 e,m 消去 e0,m0,这个步骤被称为重整化。
得到表达式的振幅应当在 Λ→∞ 时取一个有限值。上述重整化的步骤在一个可重整化理论中总是有效的,尽管在处理某些高阶微扰论时可能会比较复杂。
标量场的重整化理论
ϕ4 理论的重整化
下面以 ϕ4 理论为例说明。其拉氏量为:
L=21(∂μϕ)2−21m02ϕ2−4!λ0ϕ4(1)
其表观发散度为:
D=4−N(2)
其中 N 为外部线的数量。考虑到 ϕ4 理论在 ϕ↔−ϕ 时具有不变性,因此所有具有奇数个外部线的散射振幅必定为零。那么表观发散的图为:
我们发散上述图将包含三个发散的常数。因此我们现在的想法是:将这些发散吸收到不可观测的裸质量、裸耦合常数与场强中去。
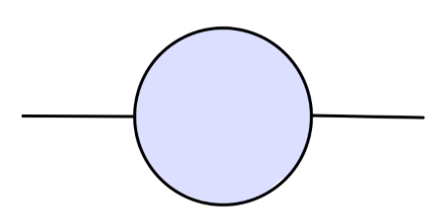
我们首先来考虑场强:
∫d4x⟨Ω∣Tϕ(x)ϕ(0)∣Ω⟩eip⋅x∼p2−m2iZ
我们可以令:
ϕ=Z1/2ϕr(3)
如此拉氏量成为:
L=21Z(∂μϕr)2−21m02Zϕr2−4!λ0Z2ϕr4(4)
通过定义:
δZδmδλ=Z−1=m02Z−m2=λ0Z2−λ(5)
我们可以消去裸耦合常数与裸质量。代入拉氏量得到:
L=21(∂μϕr)2−21m2ϕr2−4!λϕr4+21δZ(∂μϕr)2−21δmϕr2−4!δλϕr4(6)
上式子中前三项为将裸参数替换为物理参数的拉氏量,后面出现的三个含有 δ 的项称为 counterterms。
我们可以利用路径积分表述写出包含 counterterms 在内的 重整化 ϕ4 理论的费曼规则:
其值为:
p2−m2+iϵi
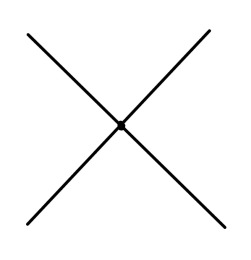
其值为:
−iλ
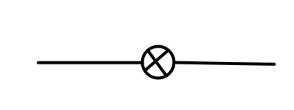
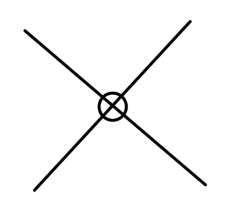
其值为:
i(p2δZ−δm)
其值为:
−iδλ
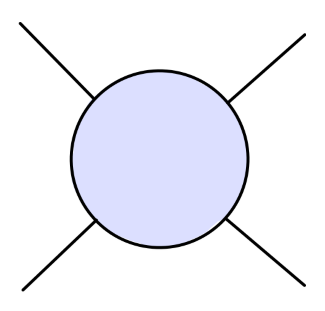
当然,只有这些是不够的。在 (5) 式中,我们引入了两个物理量:物理质量 m 与耦合参数 λ,我们需要对它们下一个明确的定义:其中物理质量 m 可以看作是传播子的极点;而耦合常数 λ 可以定义为零动量时的散射振幅。用费曼图表示为:
其值为:
p2−m2i+(terms regular at p2=m2)
其值为:
−iλat s=4m2, t=u=0
这就是 ϕ4 理论的 重整化条件 renormalization condition。
在微扰论计算中包含这些带有 counterterms 的费曼图,称为 重整化微扰论 renormalized perturbation theory。
ϕ4 重整化理论的一阶圈图计算
我们现在进行 ϕ4 重整化微扰论的一阶圈图计算。
我们先来确定重整化条件。首先考虑如下散射振幅:
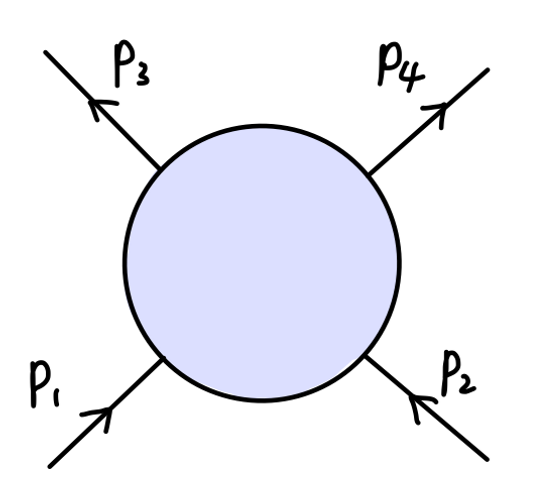
展开到一阶为:
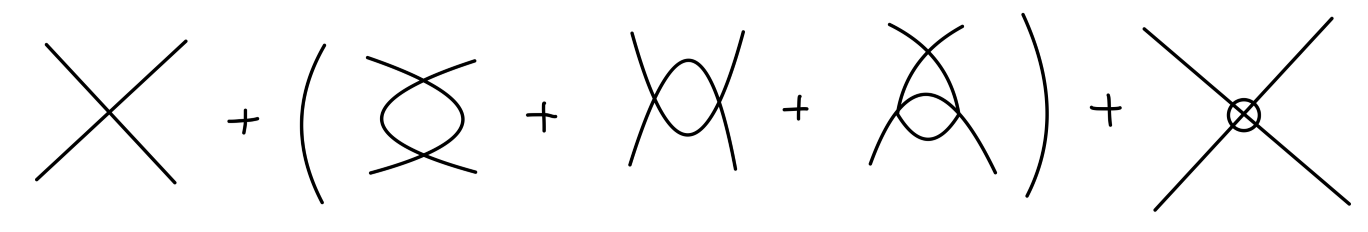
一阶圈图分别对应于 s-channel,t-channel,u-channel 三个图。再包含一个 counterterm。
考虑其中第二个图
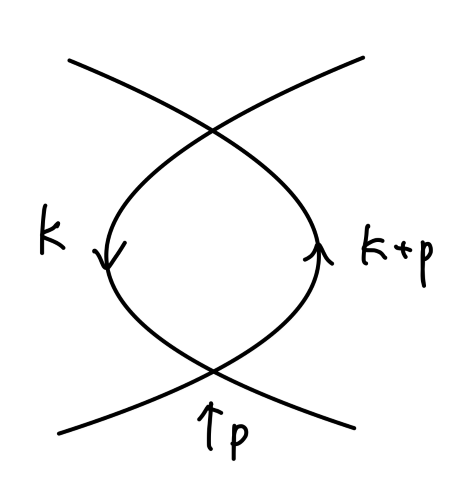
其值为:
2(−iλ)2∫(2π)4d4kk2−m2i(k+p)2−m2i≡(−iλ)2⋅iV(p2)
其中对于 s-channel,有 p2=s,对于 t-channel 与 u-channel 的图。不难得到,其值为:
(−iλ)2iV(t)and(−iλ)2iV(u)
counterterm 的值为:
−iδλ
因此,考虑所有一阶修正后,散射矩阵元成为:
iM=−iλ+(−iλ)2[iV(s)+iV(t)+iV(u)]−iδλ(7)
根据重整化条件,我们要令在 s=4m2,t=u=0 时,上述式子的值为 −iλ,即:
−iλ+(−iλ)2[iV(4m2)+iV(0)+iV(0)]−iδλ=−iλ
得到:
δλ=−λ2[V(4m2)+2V(0)](8)
利用维度正规化,我们可以得到 V(p2):
V(p2)=2−i∫(2π)dddkk2−m2i(k+p)2−m2i=2i∫01dx∫(2π)dddk[k2+2xk⋅p+xp2−m2]21l=k+xp=2i∫01dx∫(2π)dddl[l2+x(1−x)p2−m2]21lE0=−il0=−21∫01dx∫(2π)dddlE[lE2−x(1−x)p2+m2]21=−21∫01dx(4π)d/21Γ(2−2d)(m2−x(1−x)p2)2−d/21d→4⟶−32π21∫01dx(ϵ2−γ+log(4π)−log[m2−x(1−x)p2])
因此耦合常数的 shift 为:
δλ=−λ2[V(4m2)+2V(0)]=2λ2∫01dx(4π)d/2Γ(2−2d)[(m2−x(1−x)4m2)2−d/21+(m2)2−d/22]d→4⟶32π2λ2∫01dx(ϵ6−3γ+3log4π−log[m2−x(1−x)4m2]−2log[m2])
当 d→4 时,上述结果是发散的,这没有关系,δλ 并不是一个可观测量。我们将 δλ 代回到 (7) 式,将得到一个有限值:
iM=−iλ+(−iλ)2[iV(s)+iV(t)+iV(u)]−iδλ=−iλ−32π2iλ2∫01dx[log(m2−x(1−x)4m2m2−x(1−x)s)+log(m2m2−x(1−x)t)+log(m2m2−x(1−x)u)]
现在我们再来根据重整化条件确定 δZ 与 δm。
现在我们需要考虑两点关联函数。
定义所有不可约单粒子图的总和为 −iM2(p2)
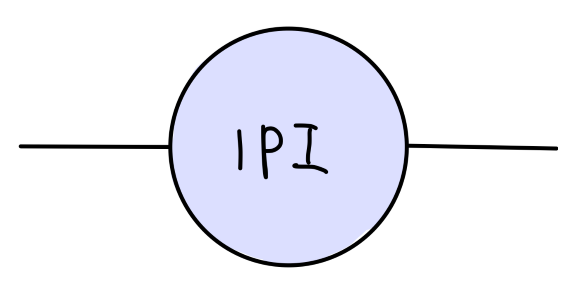
两点关联函数为:

其值为:
p2−m2−M2(p2)i
重整化条件要求上述传播子以 p=m 为极点,且对应的留数为 1,这等价于以下条件:
M2(p2)∣p2=m2=0anddp2dM2(p2)∣p2=m2=0(9)
计算到一阶图:
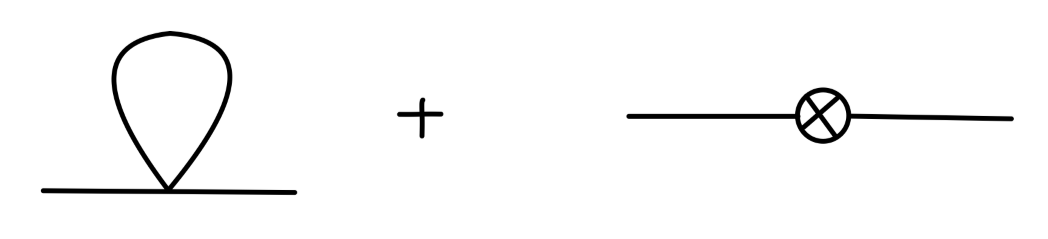
其值为:
−iM2(p2)=−iλ⋅21⋅∫(2π)dddkk2−m2i+i(p2δZ−δm)=−2iλ(4π)d/21(m2)1−d/2Γ(1−2d)+i(p2δZ−δm)
考虑到上式第一项与 p2 无关,因此只需要令:
δZ=0δm=−2(4π)d/2λ(m2)1−d/2Γ(1−2d)(10)
就能满足重整化条件。对 M2(p2),δZ 有非零贡献的来自于二阶图,这将在以后讨论。
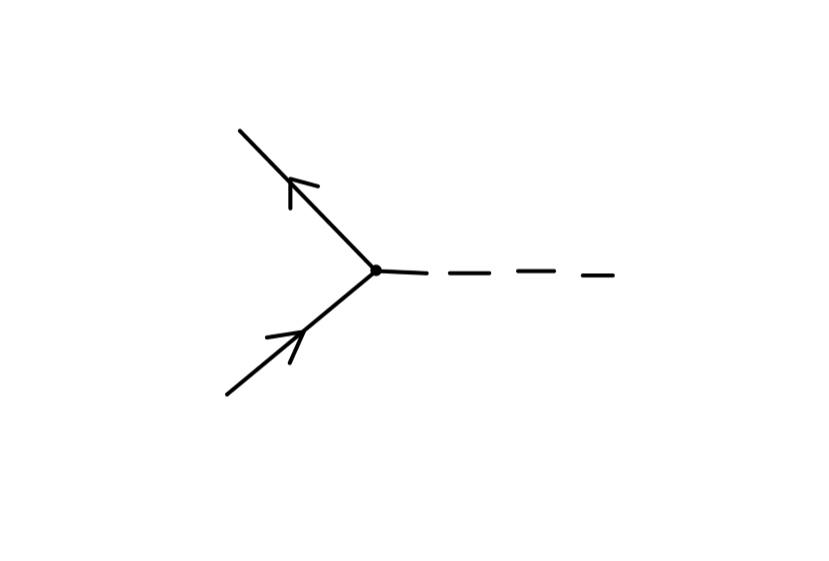
一阶图对 δZ 的贡献为零仅仅是 ϕ4 理论的特点,并不是一般的情况。例如对于 Yukawa 理论,有:
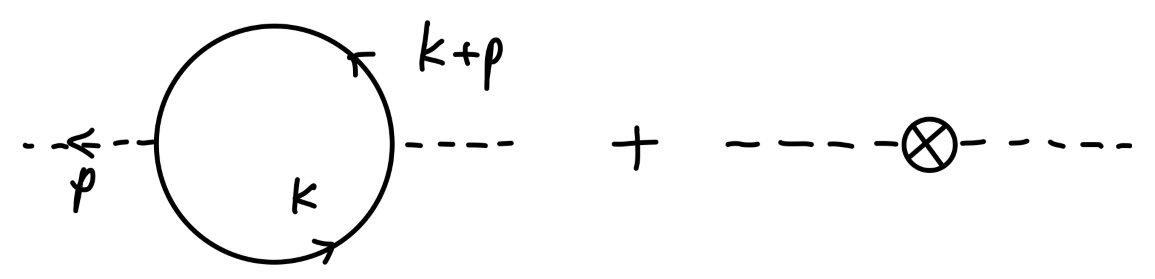
其值为:
−iM2(p2)=−(−ig)2∫(2π)dddktr[(k+p)2−mf2i(k+p+mf)k2−mf2i(k+mf)]+i(p2δZ−δm)=−4g2∫(2π)dddk((k+p)2−mf2)(k2−mf2)(k+p)⋅k+mf2+i(p2δZ−δm)
计算其中第一项:
=l=k+xp====−4g2∫(2π)dddk((k+p)2−mf2)(k2−mf2)(k+p)⋅k+mf2−4g2∫01dx∫(2π)dddk(k2+2xk⋅p+xp2−mf2)2(k+p)⋅k+mf2−4g2∫01dx∫(2π)dddl(l2+x(1−x)p2−mf2)2(l+(1−x)p)(l−xp)+mf2−4g2∫01dx∫(2π)dddl(l2+x(1−x)p2−mf2)2l2−x(1−x)p2+mf2−4g2∫01dx(4π)d/2−i(Δ1−d/22dΓ(1−2d)−Δ2−d/2ΔΓ(2−2d))(4π)d/24ig2(d−1)∫01dxΔ1−d/2Γ(1−2d)
其中 Δ=mf2−x(1−x)p2。
由重整化条件可以得到:
δm=(4π)d/24g2(d−1)∫01dx[mf2−x(1−x)m2]1−d/2Γ(1−2d)+m2δZ
为了得到 δZ,我们要利用在 p2=m2 处的导数为零的条件:
−idp2dM2(p2)∣p2=m2=(4π)d/24ig2(d−1)∫01dxx(1−x)Δ2−d/2Γ(2−2d)+iδZ=0
得到:
dp2dM2(p2)∣p2=m2=−(4π)d/24g2(d−1)∫01dx(mf2−x(1−x)p2)2−d/2x(1−x)Γ(2−2d)d→4⟶−4π23g2∫01dxx(1−x)(ϵ2−γ−32+log(4π)−log(mf2−x(1−x)m2))
QED 的重整化理论
QED 的重整化理论
现在讨论 QED 的重整化理论
QED 的拉氏量为:
L=−41(Fμν)2+ψˉ(i∂−m0)ψ−e0ψˉγμψAμ(11)
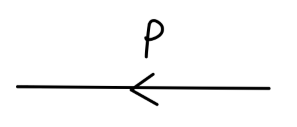
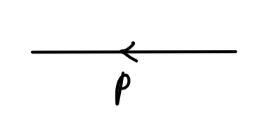
电子传播子为:
其值为:
p−miZ2
光子传播子为:
其值为:
q2−iZ3gμν
考虑到电子传播子与光子传播子的形式,为了将 Z2,Z3 吸收进拉氏量,我们如下定义:
ψ=Z21/2ψrAμ=Z31/2Arμ
如此拉氏量成为:
L=−41Z3(Frμν)2+Z2ψˉr(i∂−m0)ψr−Z2Z31/2e0ψˉrγμψrArμ(12)
我们定义物理电荷量 e 为在很远处测得的电荷量(q=0),我们可以定义 Z1:
e0Z2Z31/2=eZ1
如此,这样 QED 顶点需要满足的重整化条件为,这正定义了物理电荷量:
Γμ(q=0)=γμ
令 m 为物理质量,通过引入如下 counterterms:
δm=Z2m0−mδ1=Z1−1=ee0Z2Z31/2−1δ2=Z2−1δ3=Z3−1(13)
可以将拉氏量写为:
L=−41(Frμν)2+ψˉr(i∂−m)ψr−eψˉrγμψrArμ−41δ3(Frμν)2+ψˉr(iδ2∂−δm)ψr−eδ1ψˉrγμψrArμ(14)
于是得到重整化 QED 的费曼规则:
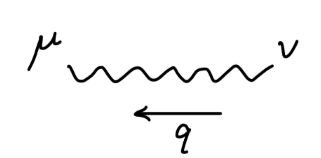
其值为:
q2+iϵ−igμν
其值为:
p−m+iϵi
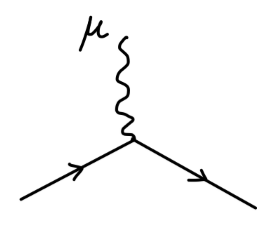
其值为:
−ieγμ
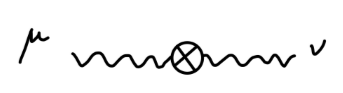
其值为:
−i(gμνq2−qμqν)δ3
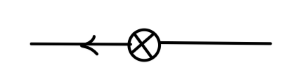
其值为:
i(pδ3−δm)
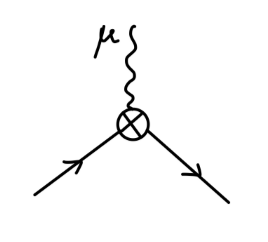
其值为:
−ieγμδ1
通过引入以下符号:
- 光子场强
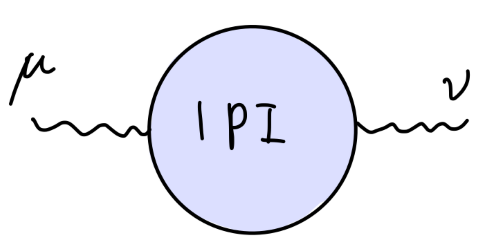
其值为
iΠμν(q)=i(gμνq2−qμqν)Π(q2)
- 电子场强
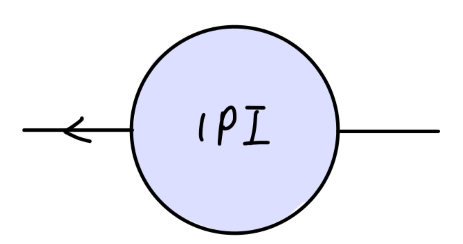
其值为
−iΣ(p)
- 电子顶点
其值为
−ieΓμ(p′,p)
可以将重整化条件写为:
Σ(p=m)=0dpdΣ(p=m)=0Π(q2=0)=0−ieΓμ(p′−p=0)=−ieγμ(15)
QED 重整化理论的一阶圈图计算
现在我们微扰论讨论到一阶。
先来看一阶的电子自能图

我们之前已经用 Pauli-Villars 正规化处理过了。现在我们不妨用维度正规化处理,得到结果为:
−iΣ2(p)=−i(4π)d/2e2∫01dx((1−x)m2+xμ2−x(1−x)p2)2−d/2Γ(2−2d)×((4−ϵ)m−(2−ϵ)xp)
因此重整化条件 (15) 中第一式成为:
Σ(p=m)=Σ2(p=m)−(mδ2−δm)=0
得到:
mδ2−δm=Σ2(p=m)=(4π)d/2e2m∫01dx((1−x)2m2+xμ2)2−d/2Γ(2−2d)⋅(4−2x−ϵ(1−x))(16)
重整化条件 (15) 中第二式成为:
dpdΣ(p=m)=dpdΣ2(p=m)−δ2=0
得到:
δ2=dpdΣ2(p=m)=−(4π)d/2e2∫01dx((1−x)2m2+xμ2)2−d/2Γ(2−2d)×[(2−ϵ)x−2ϵ(1−x)2m2+xμ22x(1−x)m2(4−2x−ϵ(1−x))](17)
再考虑一阶光子自能图:
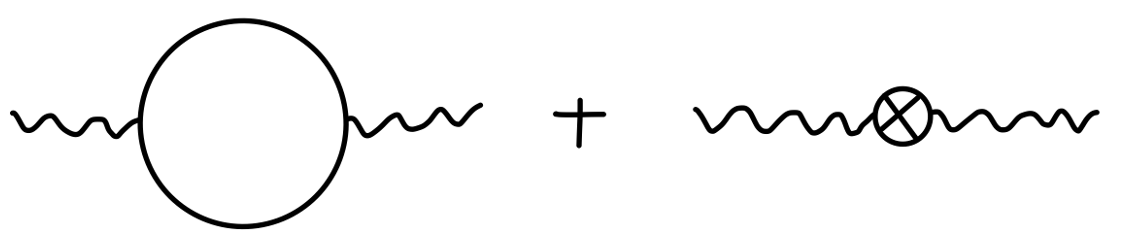
其中:
Π2(q2)=−(4π)d/2e2∫01dx(m2−x(1−x)q2)2−d/2Γ(2−2d)(8x(1−x))
重整化条件 (15) 中第三式成为:
Π(q2=0)=Π2(q2=0)−δ3=0
得到:
δ3=Π2(q2=0)=−(4π)d/2e2∫01dx(m2)2−d/2Γ(2−2d)(8x(1−x))(18)
再考虑一阶顶点修正:
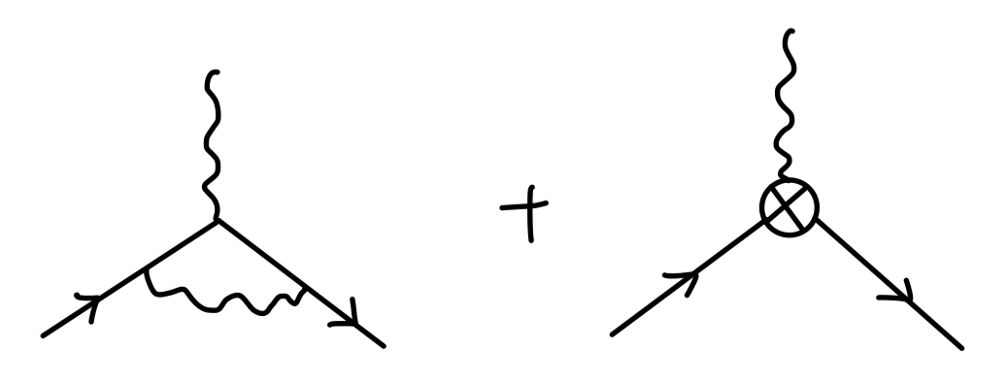
我们需要计算形状因子 F1(q2):
δF1(q2)=(4π)d/2e2∫dxdydzδ(x+y+z−1){Δ2−d/2Γ(2−2d)2(2−ϵ)2+Δ3−d/2Γ(3−2d)(q2[2(1−x)(1−y)−ϵxy]+m2[2(1−4z+z2)−ϵ(1−z)2])}
其中 Δ=(1−z)2m2+zμ2−xyq2。
重整化条件 (15) 中第四式成为:
−ieΓμ(p′−p=0)=−ieγμF1(0)−ieγμδ1=−ieγμ
得到:
δ1=−δF1(0)=(4π)d/2e2∫dz(1−z){((1−z)2m2+zμ2)2−d/2Γ(2−2d)2(2−ϵ)2+((1−z)2m2+zμ2)3−d/2Γ(3−2d)[2(1−4z+z2)−ϵ(1−z)2]m2}(19)
通过分部积分,可以得到 δ1=δ2,这意味着 Z1=Z2 在 α 阶时成立。在以前的讨论中,我们使用 Ward 等式说明了 Z1=Z2 在 α 阶时成立。那么是否 Z1=Z2 在任意阶均成立呢?我们现在来说明这个问题。
重新写出 QED 的拉氏量:
L=−41(Frμν)2+ψˉr(i∂−m)ψr−eψˉrγμψrArμ−41δ3(Frμν)2+ψˉr(iδ2∂−δm)ψr−eδ1ψˉrγμψrArμ(14)
如果我们令所有 counterterms 都等于零,剩下的部分将具有规范对称性,我们现在采用一种保持规范不变的正规化方式(例如维度正规化),这意味着 Ward 等式对于不含有 counterterms 的费曼图仍成立。这将意味着:δF1(0)=−dΣ2/dp∣m,根据重整化条件,δ1=δ2 应当成立。我们可以进行归纳讨论:如果 δ1,δ2 在 αn 阶时相等,这意味着未重整化的顶点函数在 q2=0 的值将等于 αn+1 阶电子自能图的导数,加上 counterterms 后,考虑重整化条件,我们需要令 δ1,δ2 在 αn+1 阶时相等,因此:Z1=Z2 将在任意阶成立。
这样有:
e=Z1Z2Z21/2e0=Z3e0
这正是之前所讨论的电荷重整化。
Z1=Z2 的严格成立是有深刻意义的,比如它保证了对应不同带电轻子,将给出数值相同的电荷量。例如对于 μ 子:
e=Z1′Z2′Z21/2e0=Z21/2e0
其中 Z1′,Z2′ 依赖于 μ 子质量。