广义相对论的数学基础（五）：张量

张量

多重线性映射

回想单重线性映射：线性空间 $X$ 上的线性映射就是 $X^*$ 中的向量，即这些线性映射也构成一个线性空间。现在考虑双线性映射以及多重线性映射，这些映射是否也构成一个线性空间呢？

双线性映射 (bilinear mapping)
设 $X, Y$ 和 $Z$ 为域 $\mathbb{K}$ 上的三个线性空间。若映射 $f : X ×Y \rightarrow Z$ 满足：

$\begin{aligned} & \forall x_1,x_2,x \in X,\ \forall y_1,y_2,y \in Y,\ \forall \lambda_1,\lambda_2 \in \mathbb{K}\\ &f(\lambda_1x_1 + \lambda_2x_2,y) = \lambda_1f(x_1,y) + \lambda_2f(x_2,y)\\ &f(x,\lambda_1y_1 + \lambda_2y_2) = \lambda_1f(x,y_1) + \lambda_2f(x,y_2)\\ \end{aligned}$

则称 $f$ 是一个由 $X\times Y$ 到 $Z$ 的双线性映射。

双线性映射 $f$ 对于 $X$ 或 $Y$ 中的元素分别是线性的。所有这样的双线性映射形成的集合可以表示为 $\mathscr{L}^{(2)}(X,Y;Z)$ 。

多重线性映射 (multilinear linear)
类似于双线性映射，可以定义如下的 $r$ -重线性映射：

$f : X_1\times X_2 \times\cdots \times X_r \rightarrow Z$

其中 $X_i(i = 1,\cdots,r)$ 是 $r$ 个线性空间。 $f$ 对于每一个 $X_i$ 中的元素都是线性的。同样，所有的 $r$ -重线性映射的集合可以表示为：

$\mathscr{L}^{(r)} (X_1,··· ,X_r;Z)$

类似于通常的（单重）线性映射的空间 $\mathscr{L}^{(1)}(X;Z)$ ，我们可以在 $\mathscr{L}^{(r)} (X_1,··· ,X_r;Z)$ 中引入线性结构：

$\begin{aligned} &(f + g)(x_1,··· ,x_r) = f(x_1,··· ,x_r) + g(x_1,··· ,x_r)\\ &(\lambda f)(x_1,··· ,x_r) = \lambda f(x_1,··· ,x_r)\\ \end{aligned}$

使得 $\mathscr{L}^{(r)} (X_1,··· ,X_r;Z)$ 成为一个线性空间。

之后提到的张量在本质上就是一个多重线性映射。

张量积

线性空间的张量积

设 $X, Y , W$ 是数域 $\mathbb{K}$ 上的三个线性空间。 $\mu : X × Y \rightarrow W$ 是一个双线性映射。若对任意的 $\mathbb{ K}$ 上的线性空间 $Z$ 和任意的双线性映射 $f$ ，都存在唯一的线性映射 $g : W \rightarrow Z$ 使得：

$f = g \circ \mu$

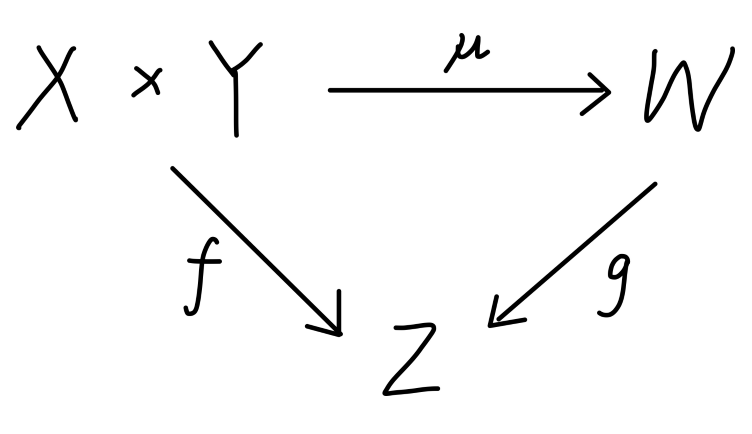
那么 $W$ 就称为是 $X$ 和 $Y$ 的 张量积 ，其中 $\mu$ 称为张量积映射。它把两个线性空间的卡氏积变成它们的张量积。

定理：张量积的存在性和唯一性
设 $X, Y$ 是数域 $\mathbb{K}$ 上的两个线性空间。则它们的张量积存在，而且在同构的意义下是唯一的。

接下来我们来构造 线性函数的“张量积”，并且这个张量积空间在同构意义下是唯一的：
设 $x^* \in X ^*, y^*\in Y^*$ 分别是 $X$ 和 $Y$ 上的线性函数，我们可以定义它们的 张量积，记为 $x^* \otimes y^*$ ，其定义如下：

$(x ^* \otimes y^* )(x',y' ) = ⟨x' ,x ^* ⟩⟨y',y^* ⟩=x^* (x') y^*(y'),\quad \forall x' \in X,\ \forall y' \in Y$

其中 $\langle x',x^*\rangle$ 为配合，将线性空间 $X$ 与其对偶空间 $X^*$ 放在对等的地位：

$⟨x' ,x ^* ⟩ = x'(x^*) = x^*(x')$

可以看出 $x^ * \otimes y^ *$ 是 $X \times Y$ 上的双线性函数（由定义容易证明）。即我们有：

$x ^* \otimes y^ * \in \mathscr{L}^{(2)} (X,Y ;\mathbb{K})$

可以很好类比得到 对偶空间的张量积： $X^ * \otimes Y^*$ 是由所有形如 $x ^* \otimes y^ *$ 的元素张成（线性组合）的线性空间。

注意并非所有 $X^* \otimes Y^*$ 中的元素可以写为 $x^* \otimes y^*$ 的形式（如量子力学中的纠缠态）。

这个空间中元素的一般形式为：

$C_{i\alpha } e^{*i} \otimes h^ {*\alpha }$

其中 $\{e ^{*i} ,i = 1,··· ,n\}$ 和 $\{h^{*\alpha } ,\alpha = 1,··· ,m\}$ 分别是 $X^*$ 和 $Y^*$ 中的基（即 $X$ 和 $Y$ 的基底 $\{e_i \}$ 和 $\{h_\alpha \}$ 的对偶基）。

若系数 $C_{i\alpha }$ 可写成 $C_{i\alpha } = a_i b_\alpha$ 的形式，则该元素可写成 $x^* \otimes y^*$ 的形式，我们称其为 可分解的。

由于 $\{e^{*i} \otimes h^{*\alpha }, i = 1,···,n,\alpha = 1,···,m\}$ 是线性独立的，不难得到它们是完备的，构成 $X^* \otimes Y^*$ 的一组基底。故有：

$\dim(X^* \otimes Y^* ) = nm$

定理
设 $X,Y$ 是两个线性空间，则：

$X^* \otimes Y^* = \mathscr{L}^{(2)}(X,Y;\mathbb{K})$

由 $X^* \otimes Y^*$ 中的元素均为双重线性映射可知。

考虑到 $X$ 与 $X^*$ 互为对偶，因此可以定义 $X$ 与 $Y$ 的张量积并有：

$X \otimes Y = \mathscr{L}^{(2)}(X^*,Y^*;\mathbb{K})$

可以得到 $X\otimes Y$ 与 $X^*\otimes Y^*$ 是互为对偶的。

容易看出张量积 $\otimes$ 对其左右两个因子都是线性的。因此它定义了一个双线性映射，即 张量积映射：

$\begin{aligned} \mu : &X \times Y \rightarrow \mathscr{L}^{(2)} (X^* ,Y^ * ;\mathbb{K})\\ & (x,y) \mapsto x \otimes y\\ \end{aligned}$

以上我们首先定义了线性空间的张量积，并且指出其在同构意义下是唯一的。由此我们通过线性函数的张量积来构造张量积空间。以下，我们拓展到多重线性函数的情况。

多重线性函数的张量积

设 $x$ 和 $y$ 分别是 $r$ -重线性函数和 $s$ -重线性函数，即：

$\begin{aligned} &x\in\mathscr{L}^{(r)}(X_ 1 ,··· ,X_r ;\mathbb{K})\\ &y\in\mathscr{L}^{(s)}(Y_1 ,··· ,Y_s ;\mathbb{K})\\ \end{aligned}$

它们的张量积定义为：

$\begin{aligned} &x\otimes y(u_1 ,··· ,u_r ;v_1 ,··· ,v_s ) = x(u_1 ,··· ,u_r ) y(v_1 ,··· ,v_s )\\ &\quad \forall u_i \in X_i ,\ i = 1,···,r \quad \forall v_j \in Y_j ,\ j = 1,···,s\\ \end{aligned}$

多重线性函数的张量积仍是一个多重线性函数，即 $x \otimes y$ 是一个 $(r + s)$ -重线性函数：

$x \otimes y : X_1 × ··· × X_r × Y_1 × ···Y_s \rightarrow \mathbb{K}$

多重线性函数的张量积满足 结合律，即：

$(x \otimes y) \otimes z = x \otimes (y \otimes z)$

其中 $x$ ， $y$ 和 $z$ 是三个多重线性函数。我们可以无歧义的将三个多重线性函数的张量积写为：

$x\otimes y\otimes z$

同理，我们也可以定义任意有限个线性空间的张量积。

张量

我们通常遇到的线性空间的张量积为如下形式：

$X_s^r=\underbrace{X \otimes ··· \otimes X}_{r}\otimes\underbrace{X^* \otimes ··· \otimes X^* } _ {s}$

即 $r$ 个 $X$ 和 $s$ 个 $X^*$ 作张量积，其中 $X^*$ 是 $X$ 的对偶空间。

注意：这里为了书写简单我们将 $X_s^r$ 中的 $X$ 和 $X^*$ 放在一起了，实际情况它们的顺序并不固定。由于书写方法的限制当然会出现一些问题，如 $X_{1}^{2}$ 可以表示：

$X\otimes X \otimes X^*\quad X\otimes X^* \otimes X\quad X^*\otimes X \otimes X$

线性空间 $X^r_s$ 的元素，称为 $(r,s)$ -型张量。 $r$ 称为张量的 逆变阶数， $s$ 称为 协变阶数。

一些特殊情况

$\begin{aligned} &X_0^0=\mathbb{K}\\ &X_0^1=X\\ &X^0_1=X^* \\ &X_0^r=\underbrace{X\otimes\cdots\otimes X}_{r}\\ &X_s^0=\underbrace{X^* \otimes\cdots\otimes X^* }_{s}\\ \end{aligned}$

张量空间 $X_{s}^{r}$ 的维数为：

$\dim (X_{s}^{r}) = (\dim(X))^{r+s}$

张量实质上是一种特殊的多重线性函数，相应构成的张量空间可以写为：

$\begin{aligned} X_s^r&=\mathscr{L}^{(r+s)}(\underbrace{X^*,\cdots,X^* }_{r},\underbrace{X,\cdots, X}_{s};\mathbb{K})\\ &=\mathscr{L}^{(1)}(\underbrace{X^* \otimes\cdots\otimes X^* }_{r}\otimes\underbrace{X\otimes\cdots\otimes X}_{s};\mathbb{K})\\ \end{aligned}$

对于张量，我们也具有多种角度进行观察。例如，张量 $X_{1}^{1}=\mathscr{L}^{(2)}(X,X^*;\mathbb{K})$ 有三种看法：

$X\times X^*\rightarrow\mathbb{K}$ 的双线性函数 $\mathscr{L}^{(2)}(\cdot,\cdot;\mathbb{K})$

$X\rightarrow X^*$ 的线性函数 $\mathscr{L}^{(2)}(\cdot,X^*;\mathbb{K})$

$X^* \rightarrow X$ 的线性函数 $\mathscr{L}^{(2)}(X,\cdot;\mathbb{K})$

张量在基底下的表示

设 $x \in X^r_s$ ，则我们可以将其表示为：

$x = x^{i_1 ···i_r}_{\qquad j_1 ···j_s} e_{i_1} \otimes\cdots \otimes e_{i_r} \otimes e^{*j_1} \otimes \cdots \otimes e^{*j_s}$

其中

$x^{i_1 ···i_r}_{\qquad j_1 ···j_s} \in\mathbb{K}$

称为张量 $x$ 在基底

$\{e_{i_1} \otimes \cdots\otimes e_{i_r} \otimes e^{*j_1} \otimes \cdots\otimes e^{*j_s}\}$

下的系数。

考虑 $X$ 中基的变换：

$e_i \rightarrow \tilde{e}_i = A^{\ \ k}_ie_k$

则对偶基的变换为：

$e^{* i} \rightarrow \tilde{e}^{* i} = (A^{-1})^{\ \ i}_ke^{* k}$

系数 $x^{i_1 ···i_r}_{\qquad j_1 ···j_s}$ 的变换法则为：

$x^{i_1 ···i_r}_{\qquad j_1 ···j_s}=\tilde{x}^{k_1 ···k_r}_{\qquad l_1 ···l_s}A_{k_1}^{\ \ i_1}\cdots A_{k_r}^{\ \ i_r}(A^{-1}) _ {j_1}^{\ \ l_1}\cdots (A^{-1}) _ {j_r}^{\ \ l_r}$

注意张量并不依赖于基底，在基的变换下不变。

张量的缩并

缩并 (contraction) 是一个将 $(r,s)$ -型张量变成一个 $(r - 1,s - 1)$ -型张量的映射，即：

$C : X^r_s\rightarrow X^{r-1}_{s-1}$

设 $1\leqslant l\leqslant s, 1\leqslant m \leqslant s$ ，张量 $x\in X^r_s$ ，那么 $C(x)\in X^{r-1}_{s-1}$ ，对应的缩并运算定义为：

$\begin{aligned} &C_l^{\ \ m} (x)(f^1 ,··· ,f^{r-1} ,u_1 ,··· ,u_{s-1} )\\=& \delta_i^{\ \ j} x(f ^1 ,··· ,f^{m-1} ,e^{*i} ,f^m ···f^{r-1},u_1 ,··· ,u_{l-1},e_j ,u_l ,···u_{s-1}) \end{aligned}$

其中

$f^i \in X^* ,i = 1,··· ,r - 1; u_j \in X ,j = 1,··· ,s - 1$

用分量表示为：

$\begin{aligned} &\delta_i^{\ \ j} x(f ^1 ,··· ,f^{m-1} ,e^{*i} ,f^m ···f^{r-1},u_1 ,··· ,u_{l-1},e_j ,u_l ,···u_{s-1}) \\ =& x^{i_1\cdots i_{m-1}ki_{m}\cdots i_{r-1}}_{\qquad\qquad\quad\ \ j_1\cdots j_{l-1}tj_l\cdots j_{s-1}} \delta_i^{\ \ j} [ e_{i_1}\otimes \cdots \otimes e_{i_{m-1}}\otimes e_{k} \otimes e_{m} \otimes \cdots \otimes e_{i_{r-1}}\\ &\otimes e^{*j_1}\otimes \cdots \otimes e^{*j_{l-1}}\otimes e^{*t}\otimes e^{*j_{l}}\otimes \cdots \otimes e^{*j_{s-1}}\\ &(f ^1 ,··· ,f^{m-1} ,e^{*i} ,f^m ···f^{r-1},u_1 ,··· ,u_{l-1},e_j ,u_l ,···u_{s-1})]\\ =&x^{i_1\cdots i_{m-1}ki_{m}\cdots i_{r-1}}_{\qquad\qquad\quad\ \ j_1\cdots j_{l-1}tj_l\cdots j_{s-1}} [ e_{i_1}\otimes\cdots \otimes e_{i_{r-1}}\otimes e^{*j_1}\otimes \cdots \otimes e^{*j_{s-1}}\\ &(f^1,\cdots,f^{r-1},u_1,\cdots,u_{s-1})]\delta_i^{\ \ j}\langle e_k,e^{*i}\rangle\langle e_j,e^{*t}\rangle\\ =&x^{i_1\cdots i_{m-1}ii_{m}\cdots i_{r-1}}_{\qquad\qquad\quad\ \ j_1\cdots j_{l-1}jj_l\cdots j_{s-1}} \delta_{i}^{\ \ j} [ e_{i_1}\otimes\cdots \otimes e_{i_{r-1}}\otimes e^{*j_1}\otimes \cdots \otimes e^{*j_{s-1}}\\ &(f^1,\cdots,f^{r-1},u_1,\cdots,u_{s-1})]\\ \end{aligned}$

因此做缩并运算后的分量可以表示为：

$(C^m_l(x))^{i_1\cdots i_{r-1}}_{\qquad\ \ \ j_1\cdots j_{s-1}} = \delta_{i}^{\ \ j}x^{i_1\cdots i_{m-1}ii_{m}\cdots i_{r-1}}_{\qquad\qquad\quad\ \ j_1\cdots j_{l-1}jj_l\cdots j_{s-1}}$

例
对于 $(1,1)$ 型张量： $x = x^{i}_{\ \ j}e_i\otimes e^{*j}$ ，缩并为：

$C_{1}^{\ \ 1}(x) = x^{i}_{\ \ i}$

抽象指标

张量的抽象指标表示是一种在张量上附加指标的一种表示。

例如：对前面的 $(r,s)$ -型张量 $x$ ，我们可以将其表示为：

$x^{a_1 \cdots a_r}_{\qquad b_1 \cdots b_s}$

指标反映出张量的类型，但并不要求选取某个基底。它不代表 $x$ 在某个基底下的分量。

例如: 张量类型 $x^{ab\ \ \ \ \ e}_{\ \ \ \ cd}$ ，它是一个多重线性映射：

$x : X ^* × X ^* × X × X × X ^* \rightarrow \mathbb{K}$

需要指出的是：指标反映类型即可，但在张量的运算或方程中，我们需要考虑到 指标的平衡。

我们将上下同时出现的求和指标称为哑标，哑标符号的选取是任意的。对于非哑标，要求指标平衡，这体现在：

等式左右出现的指标相同

相同指标的类型相同（上下位置相同）

利用抽象指标，一些张量运算可以很容易的表示。

张量积的抽象指标
两个张量的张量积 $x \otimes y$ 可表示为

$x^{a_1 \cdots a_r}_{\qquad b_1 \cdots b_s}\otimes y^{a_{r+1} \cdots a_{r+p}}_{\qquad\quad\ b_{s+1} \cdots b_{s+q}}$

或者将张量积符号省去为：

$x^{a_1 \cdots a_r}_{\qquad b_1 \cdots b_s} y^{a_{r+1} \cdots a_{r+p}}_{\qquad\quad\ b_{s+1} \cdots b_{s+q}}$

指标反映张量积的可交换性。通常来说 $x \otimes y\neq y \otimes x$ 。在抽象指标表示下， $x \otimes y$ 的交换性体现在指标是否可交换上。

基底的抽象指标形式
设 $\{e_i \}$ 为 $X$ 的一组基， $\{e^{*i} \}$ 为对偶基。则 $e_i$ 是逆变矢量， $e^{*i}$ 是协变矢量。用抽象指标形式表示为：

$(e_i)^a , (e^{*i})_ a$

缩并操作
重复的上下指标表示对这两个指标求缩并：

$\begin{aligned} &(C^m_l(x) ) ^{a_1 \cdots a_{m-1} a_{m} \cdots a_{r-1}} _ {\qquad \qquad\qquad b_1 \cdots b_{l-1} b_l \cdots b_{ s-1}}\\ &\quad =x^{a_1 \cdots a_{m-1} aa_{m} \cdots a_{r-1}} _ {\qquad \qquad\qquad\ b_1 \cdots b_{l-1} ab_l \cdots b_{ s-1}} \end{aligned}$