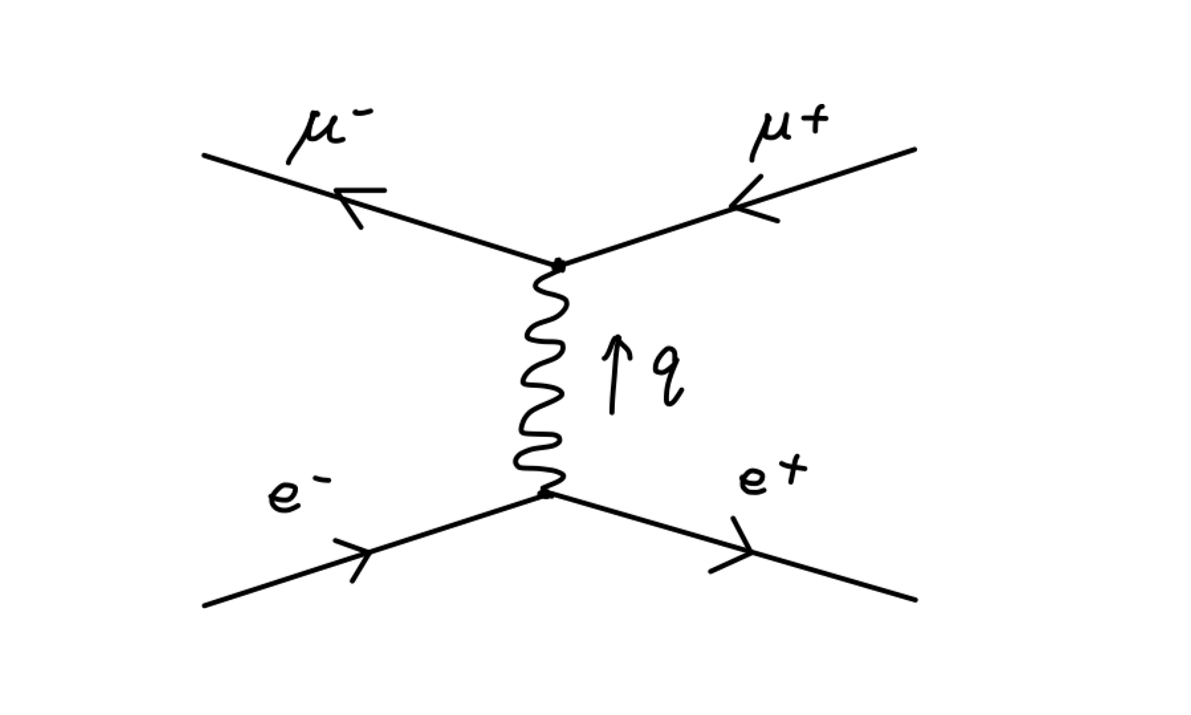
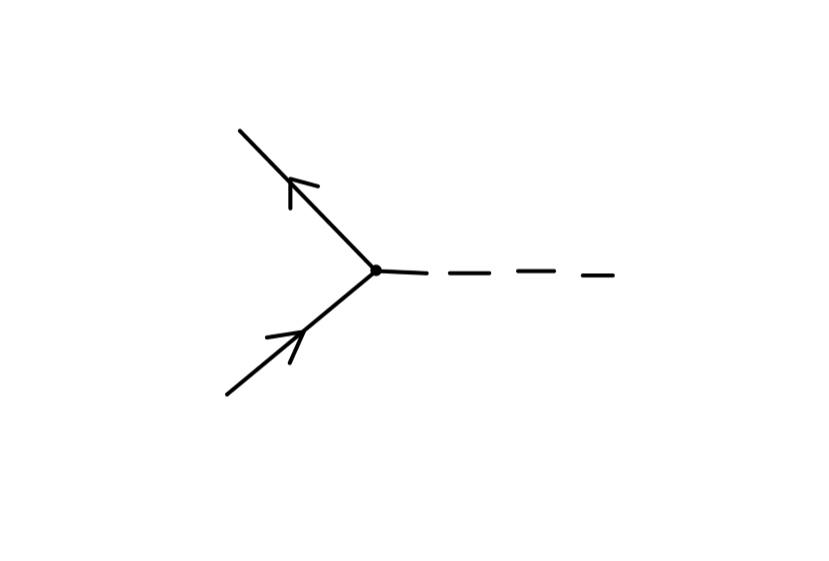
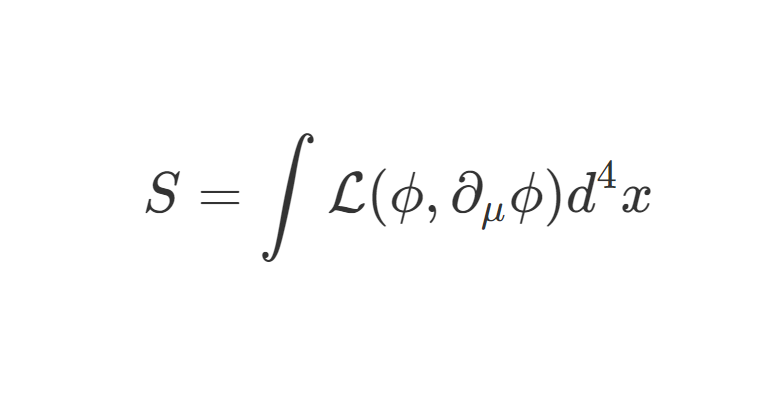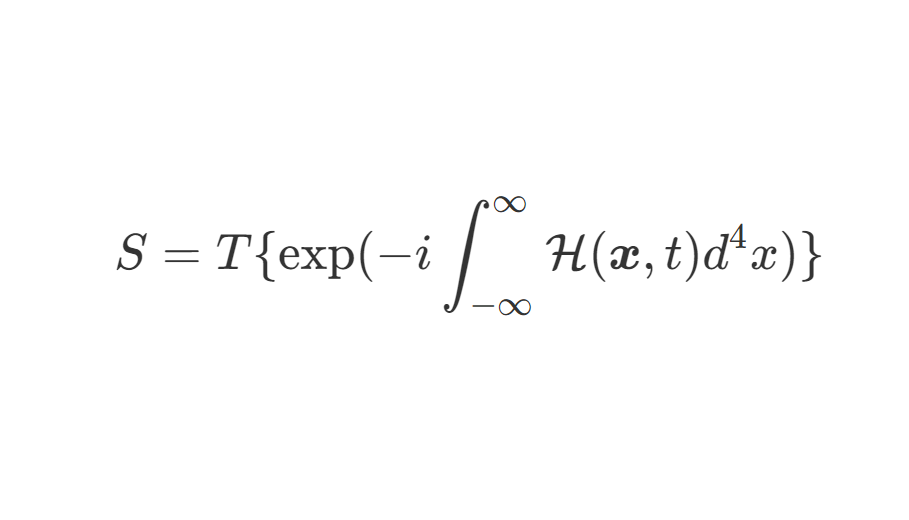现在我们想利用路径积分表述来对电磁场与旋量场进行量子化。
电磁场的量子化
在很早我们就通过假定的方式给出了光子传播子的费曼规则:
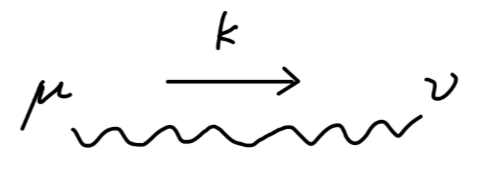
k2+iϵ−igμν(1)
现在我们利用路径积分表述来推导这件事情。
通过分部积分与傅里叶变换,可以将自由电磁场的作用量写为:
S[A]=∫d4x[−41(Fμν)2]=∫d4x[−41FμνFμν]=∫d4x[−41(∂μAν−∂νAμ)Fμν]=∫d4x[41(Aν∂μ−Aμ∂ν)(∂μAν−∂νAμ)]=21∫d4xAμ(x)(∂2gμν−∂μ∂ν)Aν(x)=21∫d4x∫(2π)8d4kd4k′e−i(k+k′)⋅xA~μ(k)(−k′2gμν+k′μk′ν)A~ν(k′)=21∫(2π)4d4kA~μ(k)(−k2gμν+kμkν)A~ν(−k)(2)
为了计算传播子的费曼规则,我们必须计算如下泛函积分:
∫DAeiS[A](3)
其中:
DA=DA0DA1DA2DA3
我们很快发现,直接计算 (3) 式是有问题的。因为规范自由度的存在,我们可以任意的选取满足条件的 A,例如取 A~μ=kμα(k),代入 (2) 中,得到:
S[A]=0
此时 (3) 式显然是发散的。该问题等价的表述为,光子传播子 DFνρ 需要满足的方程:
or(∂2gμν−∂μ∂ν)DFνρ(x−y)=iδμ ρδ(4)(x−y)(−k2gμν+kμkν)D~Fνρ(k)=iδμ ρ
该方程是的解是不存在的,因为 4×4 矩阵 (−k2gμν+kμkν) 是奇异的。
如何解决这个问题呢?Faddeev 与 Popov 提出:我们可以增加一个规范固定条件:
G(A)=0(4)
其中 G(A) 是一个规范场的函数,例如 G(A)=∂μAμ 对应于洛伦兹规范。现在我们只将那些满足规范条件的规范场考虑进来。为此,我们需要插入一个恒等算子:
1=∫DG(Aα)δ(G(Aα))=∫Dα(x)δ(G(Aα))det(δαδG(Aα))(5)
其中 Aα 表示经过如下规范变换后的场:
Aμα(x)=Aμ(x)+e1∂μα(x)(6)
对于洛伦兹规范有:
G(Aα)=∂μAμ+e1∂2α(x)(7)
如此泛函行列式成为:
det(δαδG(Aα))=det(e1∂2)
形式上成为一个与 A 无关的量,我们需要用到这个性质。
那么插入恒等算子 (5) 后,(3) 式成为:
∫DAeiS[A]=det(δαδG(Aα))∫Dα∫DAeiS[A]δ(G(Aα))=det(δαδG(Aα))∫Dα∫DAαeiS[Aα]δ(G(Aα))=det(δαδG(Aα))∫Dα∫DAeiS[A]δ(G(A))(8)
其中第二行利用了 DA=DAα,S[A]=S[Aα],第三行将 Aα 重命名为 A。为了继续计算,我们必须选取一个规范固定函数,我们选取以下一类函数:
G[A]=∂μAμ(x)−ω(x)(9)
代入 (9) 式,得到:
∫DAeiS[A]=det(e1∂2)∫Dα∫DAeiS[A]δ(∂μAμ−ω(x))(10)
既然上式对所有的 ω(x),那么我们可以对所有的 ω(x) 进行积分,我们引入一个高斯形的权重函数。那么 (10) 式成为:
=N(ξ)∫Dωexp[−i∫d4x2ξω2]det(e1∂2)(∫Dα)∫DAeiS[A]δ(∂μAμ−ω(x))N(ξ)det(e1∂2)(∫Dα)∫DAeiS[A]exp[−i∫d4x2ξ1(∂μAμ)2](11)
其中 N(ξ) 是一个不重要的归一化常数,ξ 的值是一个可以任意选取的有限值。通过 (11) 式,我们发现,考虑规范固定之后,等价于为拉格朗日量加上额外一项:
−2ξ1(∂μAμ)2
如此,对于一个规范不变的物理量 O(A) 来说,对应的关联函数为:
⟨Ω∣TO(A)∣Ω⟩=T→∞(1−iϵ)lim∫DAexp[i∫−TTd4x[L−2ξ1(∂μAμ)2]]∫DAO(A)exp[i∫−TTd4x[L−2ξ1(∂μAμ)2]](12)
我们再来考虑光子传播子的费曼规则。此时有:
S′[A]=∫d4x[−41(Fμν)2−2ξ1(∂μAμ)2]=21∫(2π)4d4kA~μ(k)(−k2gμν+(1−ξ1)kμkν)A~ν(−k)
光子传播子 D~Fνρ(k) 满足的方程为:
(−k2gμν+(1−ξ1)kμkν)D~Fνρ(k)=iδμ ρ
得到:
D~Fνρ(k)=k2+iϵ−i(gμν−(1−ξ)k2kμkν)
ξ=0 时对应 朗道规范 Laudau gauge,有:
D~Fνρ(k)=k2+iϵ−i(gμν−k2kμkν)(13)
ξ=0 时对应 费曼规范 Feynman gauge,有:
D~Fνρ(k)=k2+iϵ−igμν(14)
本组笔记中习惯使用费曼规范。
Faddeev-Popov 过程保证了:任何从费曼图中计算出来的规范不变的关联函数将是独立于 ξ 的。并且 Ward 等式告诉我们:对于任何 QED 的矩阵元,如果其外费米子均在壳,若添加一个正比于 qμ 的项到光子传播子 Dμν(q)(即改变 ξ 的值),这个矩阵元将不变化。
旋量场的量子化
旋量场分为费米子场与玻色子场,分别遵循反对易关系与对易关系。我们以 Dirac 场,即 21-旋量场为例,它们遵循反对易关系。为了对 Dirac 场进行量子化,我们需要先了解有关反对易数:Grassmann numbers 的基本知识。
Grassmann 数
Grassmann 数的基本性质是:任意两个 Grassmann 数 θ,η 之间遵循反对易关系:
θη=−ηθ(15)
容易得到:
θ2=0(16)
因此任意一个关于 θ 的函数都可以写为如下形式:
f(θ)=A+Bθ(17)
其中 A,B 为对易数。
有关 Grassman 数的积分具有如下性质:
∫dθ[af(θ)+bg(θ)]=a∫dθf(θ)+b∫dθg(θ)
在量子场论中,我们希望作 shift:θ→θ+η 时,积分值不发生变化,即:
∫dθ(A+Bθ)=∫dθ((A+Bη)+Bθ)
再结合线性性可得,如下积分的结果只能取为 B 的倍数(通常取 1):
∫dθ(A+Bθ)=B
利用上式将得到如下结果:
∫dθ=1,∫dθ θ=1(18)
有关 Grassmann 数的积分顺序是重要的,例如:
∫dθ∫dη ηθ=+1
我们习惯上从内部的积分开始做起。
现在定义 Grassmann 数的厄密共轭:
(θη)∗=η∗θ∗=−θ∗η∗
我们定义:
θ=2θ1+iθ2,θ∗=2θ1−iθ2
且有:
∫dθ∗dθ(θθ∗)=1
现在来看高斯积分:
∫dθ∗dθe−θ∗bθ∫dθ∗dθθθ∗e−θ∗bθ=∫dθ∗dθ(1−θ∗bθ)=∫dθ∗dθ(1+θθ∗b)=b=∫dθ∗dθθθ∗(1−θ∗bθ)=∫dθ∗dθθθ∗=1(19)
现在考虑有一组共 n 个复 Grassmann 数 θi,1⩽i⩽n。我们可以对这组 Grassmann 数进行一个幺正变换:
θi′=Uijθj
那么有:
i∏θi′=n!1ϵij⋯lθi′θj′⋯θl′=n!1ϵij⋯lUii′θi′Ujj′θj′⋯Ull′θl′=n!1ϵij⋯lUii′Ujj′⋯Ull′θi′θj′⋯θl′=n!1ϵij⋯lUii′Ujj′⋯Ull′ϵi′j′⋯l′(i∏θi)=(detU)(i∏θi)
现在考虑如果对以下积分做一个幺正变换:θ→Uθ:
(i∏∫dθi∗dθi)f(θ)(20)
该变换的雅可比行列式为 1,所以积分测度不变。而考虑到 f(θ) 唯一对积分值有贡献的项将具有如下形式:
(i∏θi)(i∏θi∗)
至多相差一个倍数。那么在幺正变换下,上述式子成为:
(i∏θi)(i∏θi∗)→det(U)det(U)∗(i∏θi)(i∏θi∗)=(i∏θi)(i∏θi∗)
因此对积分变量进行幺正变换不改变 (20) 式的值。
我们可以计算如下推广的高斯积分:
(i∏∫dθi∗dθi)e−θi∗Bijθj=(i∏∫dθi∗dθi)e−∑ibiθi∗θi=i∏bi=detB(21)
用矩阵形式写出更简洁:
∫dθ†dθe−θ†Bθ=detB
以及:
(i∏∫dθi∗dθi)θkθl∗e−θi∗Bijθj=(detB)(B−1)kl(22)
用矩阵形式给出证明:
具体来说,先对上式左边进行幺正变换:
θ=Uθ′θ†=θ′†U†
使得 B 对角化:
U†BU=b=diag(b1,⋯,bi,⋯)
由此可得:
B−1=Ub−1U†
进行幺正变换后,(22) 式左边成为:
∫dθ†dθ(θθ†)kle−θ†Bθ=∫dθ′†dθ′(Uθ′θ′†U†)kle−θ′†bθ′=∫dθ′†dθ′(Ub−1U†)kle−θ′†bθ′=∫dθ′†dθ′(B−1)kle−θ′†bθ′=(detB)(B−1)kl
即与(22) 式右边形式一致,得证。上式中第三步运用了 Grassmann 数积分的性质,不妨类比 (19) 中第二式。
Dirac 场的量子化
有了关于 Grassmann 数的基础。我们现在可以对旋量场进行量子化了。现在我们可以将一个费米子场 ψ(x) 表示为:
ψ(x)=i∑ψiϕi(x)
其中 ϕi(x) 为 c-number 的函数。ψi 为 Grassmann 数。为了描述 Dirac 场,我们取 ϕi 为四分量旋量的基底。
Dirac 场的两点关联函数为:
⟨0∣Tψ(x1)ψˉ(x2)∣0⟩=∫DψˉDψexp[i∫d4xψˉ(i∂−m)ψ]∫DψˉDψexp[i∫d4xψˉ(i∂−m)ψ]ψ(x1)ψˉ(x2)(23)
其结果为:
⟨0∣Tψ(x1)ψˉ(x2)∣0⟩=det(i∂−m)det(i∂−m)∫(2π)4d4k(−i(i∂−m))−1e−ik⋅(x1−x2)=∫(2π)4d4kk−m+iϵie−ik⋅(x1−x2)=SF(x1−x2)(24)
Dirac 场的生成泛函为:
Z[ηˉ,η]=∫DψDψˉexp[i∫d4x[ψˉ(i∂−m)ψ+ηˉψ+ψˉη]](25)
其中 η 是一个 Grassmann 场。
考虑到 SF(x−y) 是 Dirac 方程的格林函数:
(i∂−m)SF(x−y)=iδ(4)(x−y)(26)
因此,可以考虑对 ψ,ψˉ 进行如下 shift:
ψψˉ=ψ′−i∫d4ySF(x−y)η(y)=ψˉ′+i∫d4ySF∗(x−y)ηˉ(y)=ψˉ′−i∫d4ySF(y−x)ηˉ(y)
代入 (25) 式,得到:
Z[ηˉ,η]=∫DψDψˉexp[i∫d4x[ψˉ(i∂−m)ψ+ηˉψ+ψˉη]]=∫Dψ′Dψˉ′exp[i∫d4x[ψˉ′(i∂−m)ψ′]exp[−∫d4xd4yη(x)SF(x−y)η(y)]=Z0exp[−∫d4xd4yηˉ(x)SF(x−y)η(y)]
即:
Z[ηˉ,η]=Z0exp[−∫d4xd4yηˉ(x)SF(x−y)η(y)](27)
有关 Grassmann 数的求导,有:
dηdθη=−θdηdηθ=θ
这样,我们可以用泛函导数与生成泛函写出两点关联函数:
⟨0∣Tψ(x1)ψˉ(x2)∣0⟩=Z0−1(−iδηˉ(x1)δ)(iδη(x2)δ)Z[ηˉ,η]∣ηˉ,η=0(28)
利用 (27) 式,立即得到上式的结果为:
⟨0∣Tψ(x1)ψˉ(x2)∣0⟩=SF(x1−x2)
QED
量子场论的路径积分表述让我们可以直接从拉氏量出发,推导费曼规则。现在我们来看 QED 的拉氏量:
LQED=ψˉ(iD−m)ψ−41(Fμν)2=ψˉ(i∂−m)ψ−41(Fμν)2−eψˉγμψAμ=L0−eψˉγμψAμ
可以进行展开:
exp[i∫L0][1−ie∫d4xψˉγμψAμ+⋯]
其中自由场部分对应如下传播子:
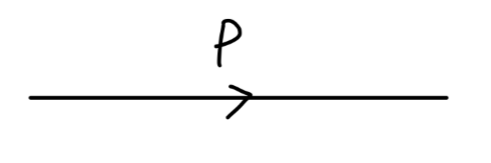
∫(2π)4d4pp−m+iϵie−ip⋅(x−y)
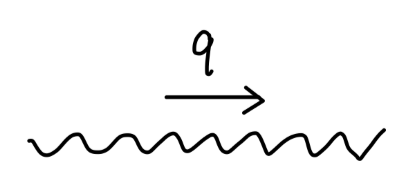
∫(2π)4d4qq2+iϵ−igμνe−iq⋅(x−y)
相互作用项给出 QED 顶点:
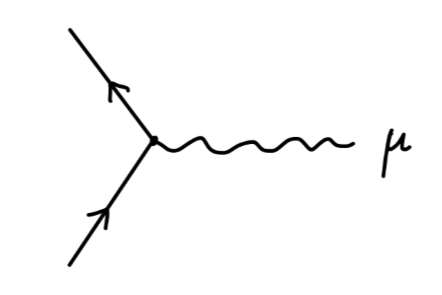
−ieγμ∫d4x
以上就是坐标空间中的费曼规则,我们将其重排后可以得到动量空间中的费曼规则。
泛函行列式
我们现在来考虑我们得到的泛函行列式的物理含义。
对于下列表达式:
∫DψˉDψexp[i∫d4xψˉ(iD−m)ψ]
其值可以表示为泛函行列式:
det(iD−m)=det(i∂−m−eA)=det(i∂−m)⋅det(1−i∂−mi(−ieA))(28)
设 bi 为 B 的本征值,那么有下列公式成立:
detB=i∏bi=exp[i∑logbi]=exp[Tr(logB)]
注意,我们现在使用 Tr() 表示对算子求迹,用 tr() 表示求 Dirac 迹。
于是 (28) 式中的如下因子可以展开为:
det(1−i∂−mi(−ieA))=exp[Trlog(1−i∂−mi(−ieA))]=exp[i=1∑∞−n1Tr[(i∂−mi(−ieA))n]]
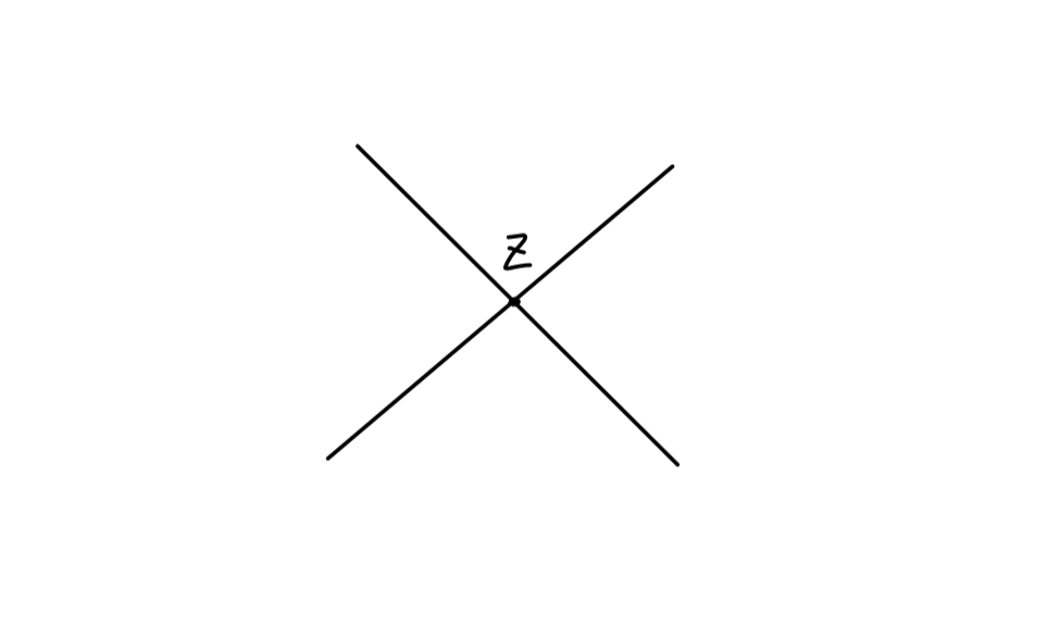
考虑以下费曼规则:
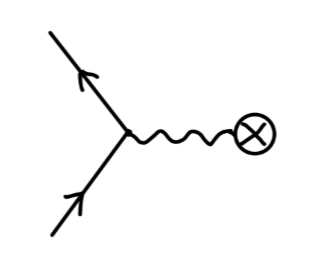
其值为:
−ieγμ∫d4xAμ(x)
可以得到费米子行列式的值为以下费曼图的和。
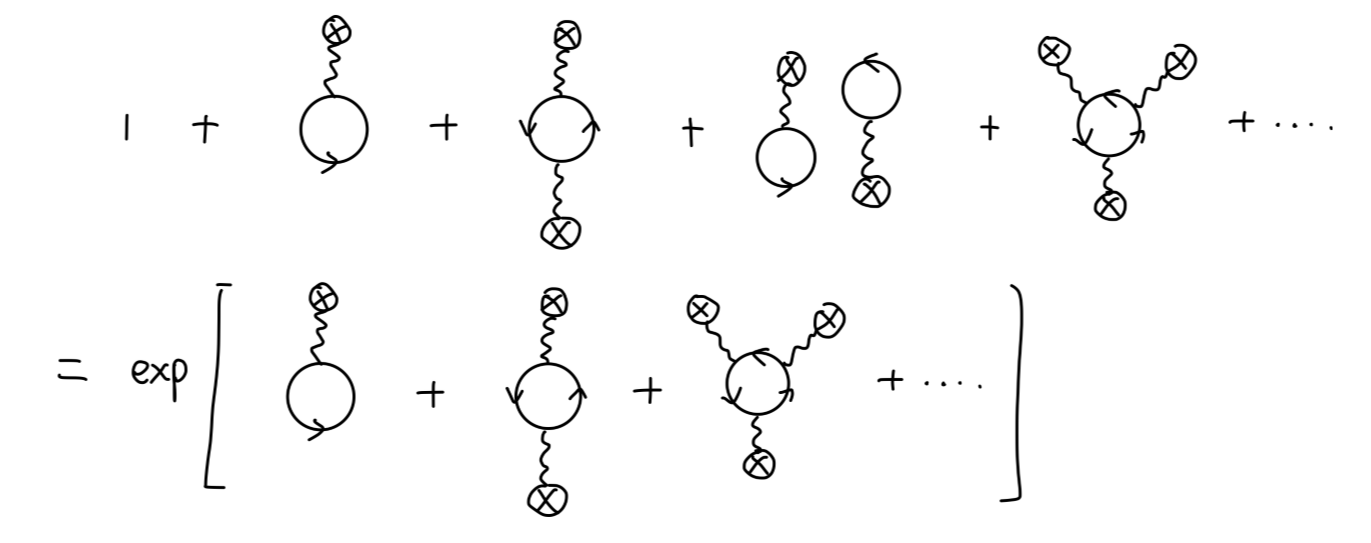
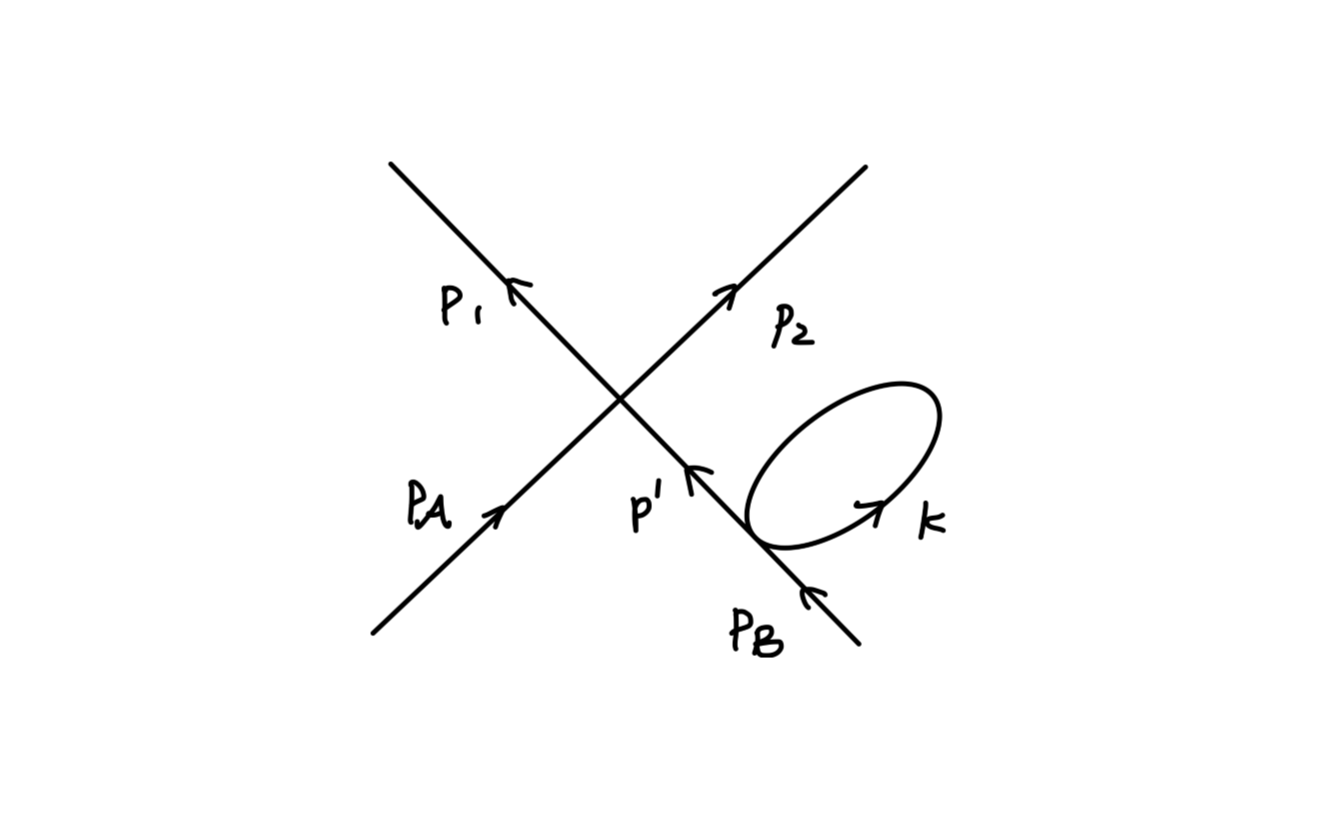
这是容易理解的。因为考虑以下图:

对应的值为:
=−n1∫dx1⋯dxntr[(−ieA(x1))SF(x2−x1)⋯(−ieA(xn))SF(x1−xn)]−n1Tr[(i∂−mi(−ieA))n]
其中因子为 1/n 而不是 1/n! 是由于:指标的顺序是重要的。