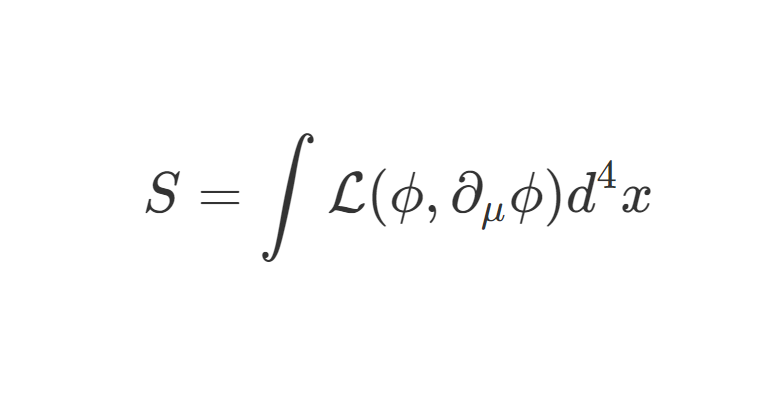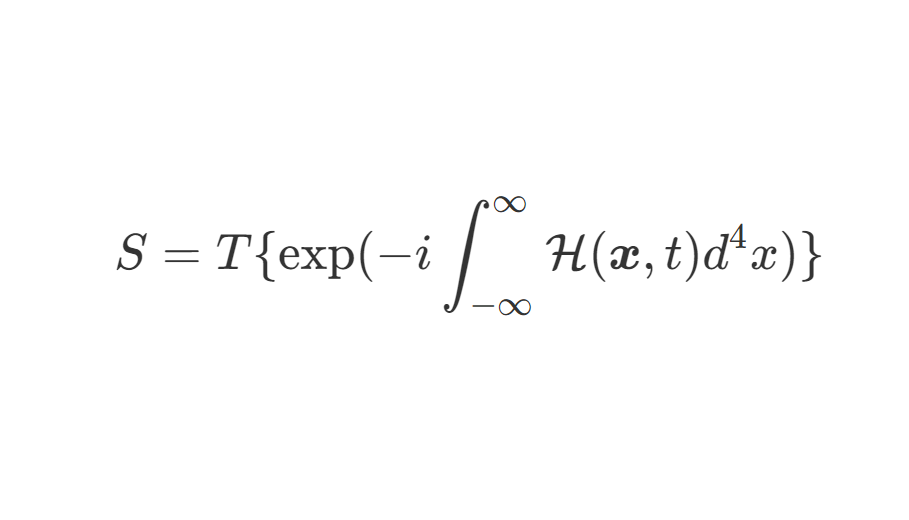电荷重整化

真空极化与电荷重整化

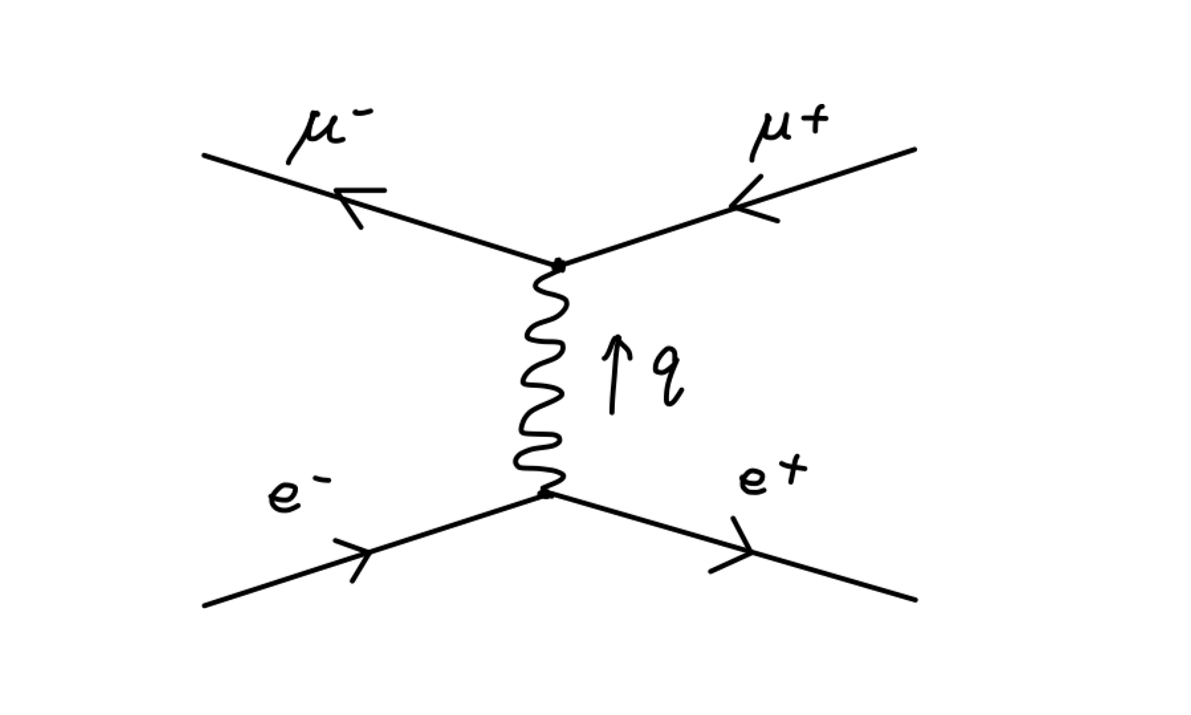
本篇我们将计算如下过程：

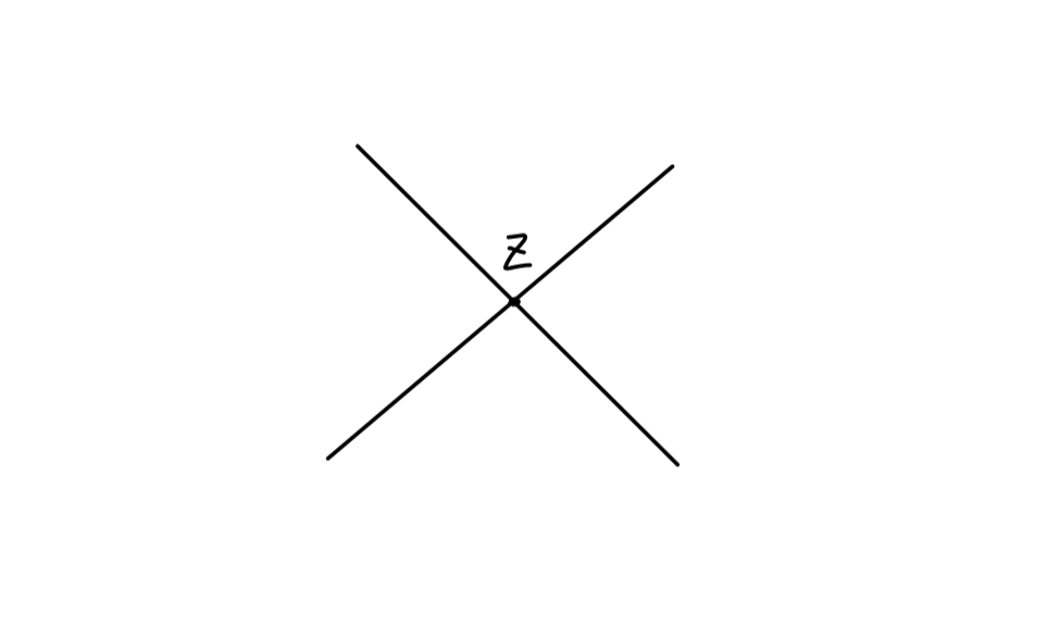
我们称之为 O(α)\mathcal{O}(\alpha) 阶的 真空极化 vacuum polarization 图。

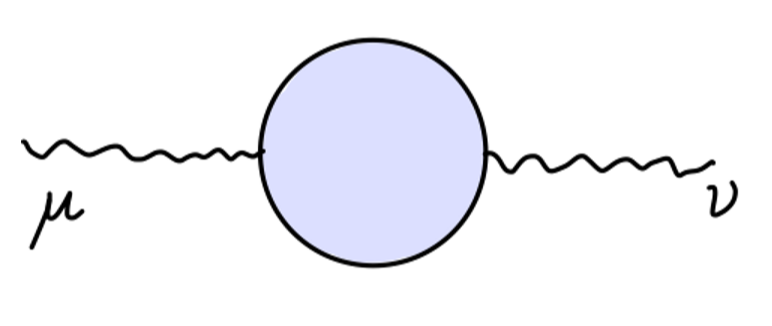
我们感兴趣的部分为中间的电子圈：

根据费曼规则，得到上述费曼图的值为：

(−ie2)(−1)∫d4k(2π)4tr[γμik−mγνik+q−m]≡iΠ2μν(q)(1)(-ie^2)(-1)\int\frac{d^4k}{(2\pi)^4}\mathrm{tr}[\gamma^{\mu}\frac{i}{\cancel{k}-m}\gamma^{\nu}\frac{i}{\cancel{k} + \cancel{q}-m}] \equiv i\Pi_2^{\mu\nu}(q)\tag{1}

光子的两点关联函数可以表示为：

我们可以将其分解为一系列单粒子不可约图的总和，即：

其中单粒子不可约图为：

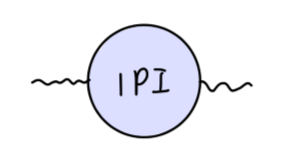
其值可以定义为：

iΠμν(q)i\Pi^{\mu\nu}(q)

在 (1)(1) 式中，我们之所以将 O(α)\mathcal{O}(\alpha) 阶真空极化图的贡献称之为 Π2\Pi_2，是因为它包含了 e2e^2，是一个对真空极化的关于 ee 的二阶贡献。

现在考虑 Πμν\Pi^{\mu\nu} 的洛伦兹结构。由于出现在 Πμν\Pi^{\mu\nu} 的张量仅可能是 gμνg^{\mu\nu} 与 qμqνq^{\mu}q^{\nu}，而由 ward 等式得：

qμΠμν=qνΠμν=0q_{\mu}\Pi^{\mu\nu} = q_{\nu}\Pi^{\mu\nu} = 0

因此可以得到：Πμν\Pi^{\mu\nu} 将正比于 gμν−qμqν/q2g^{\mu\nu} - q^{\mu}q^{\nu}/q^2。并且我们预期 Π(q2)μν\Pi(q^2)^{\mu\nu} 在 q2=0q^2=0 处不会出现极点，如此的极点将对应一个无质量粒子的中间态，这在单粒子不可约图中是不会发生的，这件事情是可以被证明的。
因此我们可以把 Πμν\Pi^{\mu\nu} 写为如下形式：

Πμν(q)=(q2gμν−qμqν)Π(q2)(2)\Pi^{\mu\nu}(q) = (q^2g^{\mu\nu} - q^{\mu}q^{\nu})\Pi(q^2)\tag{2}

那么光子两点关联函数可以写为：

−igμνq2+−igμρq2[i(q2gρσ−qρqσ)Π(q2)]−igσνq2+⋯(3)\begin{aligned} &\frac{-ig_{\mu\nu}}{q^2} + \frac{-ig_{\mu\rho}}{q^2}[i(q^2g^{\rho\sigma} - q^{\rho}q^{\sigma})\Pi(q^2)]\frac{-ig_{\sigma\nu}}{q^2} + \cdots\\ \end{aligned}\tag{3}

令 Δνρ≡δνρ−qρqν/q2\Delta_{\nu}^{\rho} \equiv \delta_{\nu}^{\rho} - q^{\rho}q_{\nu}/q^2。注意到：

ΔσρΔνσ=(δσρ−qρqσ/q2)(δνσ−qσqν/q2)=δνρ−2qρqν/q2+qρqνqσqσ/q4=δνρ−qρqν/q2=Δνρ(4)\begin{aligned} \Delta_{\sigma}^{\rho}\Delta_{\nu}^{\sigma} &= (\delta_{\sigma}^{\rho} - q^{\rho}q_{\sigma}/q^2)(\delta_{\nu}^{\sigma} - q^{\sigma}q_{\nu}/q^2)\\ &= \delta^{\rho}_{\nu} - 2q^{\rho}q_{\nu}/q^2 + q^{\rho}q_{\nu}q^{\sigma}q_{\sigma}/q^4\\ &= \delta^{\rho}_{\nu} - q^{\rho}q_{\nu}/q^2 = \Delta^{\rho}_{\nu}\\ \end{aligned}\tag{4}

应用 (4)(4) 的结果到 (3)(3) 式，我们得到：

−igμνq2+−igμρq2ΔνρΠ(q2)+−igμρq2ΔσρΔνσΠ2(q2)+⋯=−igμνq2+−igμρq2ΔνρΠ(q2)+−igμρq2ΔνρΠ2(q2)+⋯=−igμνq2+−igμρq2Δνρ(Π(q2)+Π2(q2)+⋯ )=−igμνq2+−igμρq2(δνρ−qρqνq2)Π(q2)1−Π(q2)=−iq2(1−Π(q2))(gμν−qμqνq2)+−iq2(qμqνq2)(5)\begin{aligned} &\frac{-ig_{\mu\nu}}{q^2} + \frac{-ig_{\mu\rho}}{q^2}\Delta^{\rho}_{\nu}\Pi(q^2) + \frac{-ig_{\mu\rho}}{q^2}\Delta^{\rho}_{\sigma}\Delta^{\sigma}_{\nu}\Pi^2(q^2) + \cdots\\ =& \frac{-ig_{\mu\nu}}{q^2} + \frac{-ig_{\mu\rho}}{q^2}\Delta^{\rho}_{\nu}\Pi(q^2) + \frac{-ig_{\mu\rho}}{q^2}\Delta^{\rho}_{\nu}\Pi^2(q^2) + \cdots\\ =& \frac{-ig_{\mu\nu}}{q^2} + \frac{-ig_{\mu\rho}}{q^2}\Delta^{\rho}_{\nu}(\Pi(q^2)+\Pi^2(q^2)+\cdots)\\ =& \frac{-ig_{\mu\nu}}{q^2} + \frac{-ig_{\mu\rho}}{q^2}(\delta_{\nu}^{\rho} - \frac{q^{\rho}q_{\nu}}{q^2})\frac{\Pi(q^2)}{1-\Pi(q^2)}\\ =& \frac{-i}{q^2(1-\Pi(q^2))}(g_{\mu\nu}-\frac{q_{\mu}q_{\nu}}{q^2}) + \frac{-i}{q^2}(\frac{q_{\mu}q_{\nu}}{q^2}) \end{aligned}\tag{5}

根据 Ward 等式，与 qμq_{\mu} 或 qνq_{\nu} 成正比的项将会消去。如果是计算散射矩阵，那么我们可以将上述式子简化为：

−igμνq2(1−Π(q2))(6)\frac{-ig_{\mu\nu}}{q^2(1-\Pi(q^2))}\tag{6}

其中 Π(q2)\Pi(q^2) 在 q2=0q^2=0 时是解析的。而上式子总有 q2=0q^2 = 0 的极点，因此光子在任何阶微扰论中总是为零质量的。q2=0q^2=0 时对应的留数为：

11−Π(0)≡Z3(7)\frac{1}{1-\Pi(0)} \equiv Z_3\tag{7}

现在在很多能量较低的散射过程（即 q2q^2 较小）中，例如以下过程

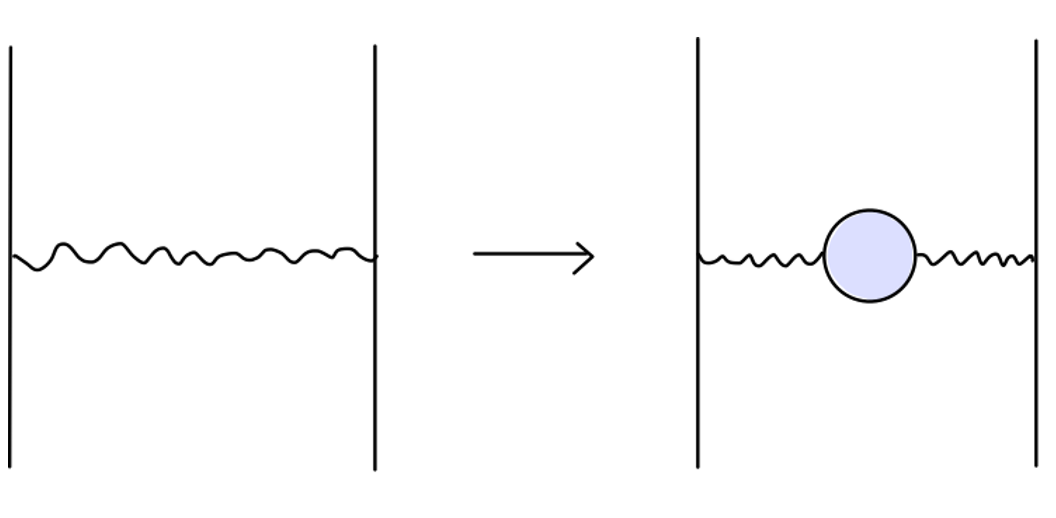
我们只需要在最终的结果中对光子传播子做以下替代：

⋯e2gμνq2⋯→⋯Z3e2gμνq2⋯\cdots \frac{e^2g_{\mu\nu}}{q^2}\cdots \rightarrow \cdots \frac{Z_3 e^2g_{\mu\nu}}{q^2}\cdots

就能够完成从上述左图到右图的转变。这也等价于对电荷量做如下替代：

e→Z3ee \rightarrow \sqrt{Z_3}e

这个过程我们称之为 电荷重整化 charge renomalization。需要理解的是，在实验中能够测得的 物理电荷量 为：Z3e\sqrt{Z_3}e，我们现在将该物理量简单记为 ee，而之前的电荷量只是一个裸参数，称之为裸电荷 e0e_0，其将出现在拉氏量中。我们总结为下式：

(physical charge)=e=Z3e0=Z3⋅(bare charge)(physical\ charge) = e = \sqrt{Z_3}e_0 = \sqrt{Z_3}\cdot(bare\ charge)

在只考虑 tree-level 的情况下，Z3=1Z_3 = 1，e=e0e=e_0。

除了对电荷的修正，Π(q2)\Pi(q^2) 还具有其他效应。例如对于一个具有非零 q2q^2 的散射过程，在考虑到 O(α)\mathcal{O}(\alpha) 阶修正的情况下有：

Π(q2)≈Π2(q2)\Pi(q^2) \approx \Pi_2(q^2)

因此下列物理量可以写为：

−igμνq2(e021−Π(q2))=−igμνq2(e021−Π(0))(1−Π(0)1−Π(q2))=O(α)−igμνq2(e21−[Π(q2)−Π(0)])\begin{aligned} \frac{-ig_{\mu\nu}}{q^2}(\frac{e_0^2}{1-\Pi(q^2)}) &=\frac{-ig_{\mu\nu}}{q^2}(\frac{e_0^2}{1-\Pi(0)})(\frac{1-\Pi(0)}{1-\Pi(q^2)})\\ &\underset{\mathcal{O}(\alpha)}{=}\frac{-ig_{\mu\nu}}{q^2}(\frac{e^2}{1-[\Pi(q^2)-\Pi(0)]})\\ \end{aligned}

这可以解释为电磁耦合常数将成为一个依赖于 q2q^2 的量：

α0→αeff(q2)=e02/4π1−Π(q2)=O(α)α1−[Π2(q2)−Π2(0)]\alpha_0 \rightarrow \alpha_{eff}(q^2) = \frac{e_0^2/4\pi}{1-\Pi(q^2)} \underset{\mathcal{O}(\alpha)}{=} \frac{\alpha}{1-[\Pi_2(q^2)-\Pi_2(0)]}

Π2\Pi_2 的计算

现在我们来计算 Π2\Pi_2，这在 (1)(1) 式中已经给出了：

iΠ2μν(q)=−(−ie)2∫d4k(2π)4tr[γμi(k+m)k2−m2γνi(k+q+m)(k+q)2−m2]=−e2∫d4k(2π)4tr[γμ(k+m)γν(k+q+m)](k2−m2)((k+q)2−m2)=−4e2∫d4k(2π)4kμ(k+q)ν+kν(k+q)μ−gμν(k⋅(k+q)−m2)(k2−m2)((k+q)2−m2)\begin{aligned} i\Pi_2^{\mu\nu}(q) &= -(-ie)^2\int \frac{d^4k}{(2\pi)^4}\mathrm{tr}[\gamma^{\mu}\frac{i(\cancel{k}+m)}{k^2-m^2}\gamma^{\nu}\frac{i(\cancel{k}+\cancel{q}+m)}{(k+q)^2-m^2}]\\ &= -e^2 \int \frac{d^4k}{(2\pi)^4}\frac{\mathrm{tr}[\gamma^{\mu}(\cancel{k}+m)\gamma^{\nu}(\cancel{k}+\cancel{q}+m)]}{(k^2-m^2)((k+q)^2-m^2)}\\ &= -4e^2\int \frac{d^4k}{(2\pi)^4}\frac{k^{\mu}(k+q)^{\nu}+k^{\nu}(k+q)^{\mu}-g^{\mu\nu}(k\cdot(k+q)-m^2)}{(k^2-m^2)((k+q)^2-m^2)} \end{aligned}

引入费曼参数化，可以将分母写为：

1(k2−m2)((k+q)2−m2)=∫01dx1(k2+2xk⋅q+xq2−m2)2=l=k+xq∫01dx1l2+x(1−x)q2−m2\begin{aligned} \frac{1}{(k^2-m^2)((k+q)^2-m^2)} &= \int_{0}^{1}dx \frac{1}{(k^2+2xk\cdot q + xq^2 -m^2)^2}\\ &\underset{l = k + xq}{=} \int_{0}^{1}dx \frac{1}{l^2 + x(1-x)q^2-m^2} \end{aligned}

那么分子成为：

(l−xq)μ(l+(1−x)q)ν+(l−xq)ν(l+(1−x)q)μ−gμν((l−xq)⋅(l+(1−x)q)−m2)=2lμlν−gμνl2−2x(1−x)qμqν+gμν(m2+x(1−x)q2)+(terms linear in l)\begin{aligned} &(l-xq)^{\mu}(l+(1-x)q)^{\nu} + (l-xq)^{\nu}(l+(1-x)q)^{\mu} - g^{\mu\nu}((l-xq)\cdot(l+(1-x)q)-m^2)\\ =& 2l^{\mu}l^{\nu} -g^{\mu\nu}l^2 - 2x(1-x)q^{\mu}q^{\nu} + g^{\mu\nu}(m^2 + x(1-x)q^2) + (terms\ linear\ in\ l) \end{aligned}

这里我们将有关 ll 的线性项放在一边，因为根据对称性，这些项的积分将没有贡献。现在我们作 Wick rotation，令 l0=ilE0l^0 = il_E^0，得到：

iΠ2μν(q)=−4ie2∫01dx∫d4lE(2π)4−2lEμlEν+gμνlE2−2x(1−x)qμqν+gμν(m2+x(1−x)q2)(lE2+Δ)2=−4ie2∫01dx∫d4lE(2π)4−12gμνlE2+gμνlE2−2x(1−x)qμqν+gμν(m2+x(1−x)q2)(lE2+Δ)2\begin{aligned} i\Pi_2^{\mu\nu}(q) &= -4ie^2\int_{0}^{1}dx\int \frac{d^4l_E}{(2\pi)^4} \frac{-2l_E^{\mu}l_E^{\nu} +g^{\mu\nu}l_E^2 - 2x(1-x)q^{\mu}q^{\nu} + g^{\mu\nu}(m^2 + x(1-x)q^2)}{(l_E^2 + \Delta)^2}\\ &= -4ie^2\int_{0}^{1}dx\int \frac{d^4l_E}{(2\pi)^4} \frac{-\frac{1}{2}g^{\mu\nu}l_E^2 +g^{\mu\nu}l_E^2 - 2x(1-x)q^{\mu}q^{\nu} + g^{\mu\nu}(m^2 + x(1-x)q^2)}{(l_E^2 + \Delta)^2}\\ \end{aligned}

其中：

Δ=m2−x(1−x)q2\Delta = m^2 - x(1-x)q^2

上述积分将是严重发散的，若我们引入一个截断 lE=Λl_E = \Lambda，将得到：

iΠ2μν(q)∝e2Λ2gμνi\Pi^{\mu\nu}_2(q) \propto e^2\Lambda^2g^{\mu\nu}

这是一件非常糟糕的事情。因为它将给出一个无穷大的光子质量，并且将违反 Ward 等式，这显然是不正确的。问题的根源是我们不能很 naive 的选取一个截断进行计算，而应该选取一种特定的正规化方式。我们可以使用 Pauli-Villars 正规化去做这件事情，但比较繁琐，下面我们介绍较为简单的 维度正规化 Dimensional Regularization 方法。

维度正规化

维度正规化所采用的方法是：我们假设费曼图的值是一个时空维度 dd 的解析函数。那么对于任何充分小的 dd，对应的圈积分将会收敛，我们最后只需要考虑将 d→4d\rightarrow 4，就能够得到一些 well-defined 的结果。

我们现在考虑一个 dd 维的时空，其中 11 维为时间，d−1d-1 维为空间。在进行 Wick 旋转后，例如考虑以下积分：

∫ddlE(2π)d1(lE2+Δ)2=∫dΩd(2π)d⋅∫0∞dlElEd−1(lE2+Δ)2(8)\int \frac{d^dl_E}{(2\pi)^d}\frac{1}{(l_E^2+\Delta)^2} = \int \frac{d\Omega_d}{(2\pi)^d}\cdot \int_{0}^{\infty}dl_E \frac{l_E^{d-1}}{(l_E^2+\Delta)^2}\tag{8}

其中 Ωd\Omega_d 为 dd 维立体角，有：

(π)d=(∫dxe−x2)d=∫ddxexp⁡(−∑i=1dxi2)=∫dΩd∫0∞dxxd−1e−x2=(∫dΩd)⋅12∫0∞dx2(x2)d2−1e−(x2)=(∫dΩd)⋅12Γ(d2)\begin{aligned} (\sqrt{\pi})^d &= (\int dx e^{-x^2})^d\\ &= \int d^dx \exp(-\sum_{i=1}^d x_i^2)\\ &= \int d\Omega_d \int_{0}^{\infty}dx x^{d-1}e^{-x^2}\\ &= (\int d\Omega_d)\cdot \frac{1}{2}\int_{0}^{\infty}dx^2 (x^2)^{\frac{d}{2}-1}e^{-(x^2)}\\ &= (\int d\Omega_d) \cdot \frac{1}{2}\Gamma(\frac{d}{2}) \end{aligned}

因此得到：

∫dΩd=2πd/2Γ(d/2)(9)\int d\Omega_d = \frac{2\pi^{d/2}}{\Gamma(d/2)}\tag{9}

考虑 (8)(8) 式中的如下积分的值为：

∫0∞dlld−1(l2+Δ)2=12∫0∞d(l2)(l2)d2−1(l2+Δ)2=12(1Δ)2−d2∫01dxx1−d2(1−x)d2−1=12(1Δ)2−d2Γ(d2)Γ(2−d2)Γ(2)(10)\begin{aligned} \int_{0}^{\infty}dl \frac{l^{d-1}}{(l^2+\Delta)^2} &= \frac{1}{2}\int_{0}^{\infty}d(l^2)\frac{(l^2)^{\frac{d}{2}-1}}{(l^2+\Delta)^2}\\ &= \frac{1}{2} (\frac{1}{\Delta})^{2-\frac{d}{2}}\int_{0}^{1}dx x^{1-\frac{d}{2}}(1-x)^{\frac{d}{2}-1}\\ &= \frac{1}{2} (\frac{1}{\Delta})^{2-\frac{d}{2}} \frac{\Gamma(\frac{d}{2})\Gamma(2-\frac{d}{2})}{\Gamma(2)}\\ \end{aligned}\tag{10}

其中作了代换：x=Δ/(l2+Δ)x=\Delta/(l^2+\Delta)，并且使用了以下积分公式：

∫01xα−1(1−x)β−1=B(α,β)=Γ(α)Γ(β)Γ(α+β)\int_{0}^{1}x^{\alpha-1}(1-x)^{\beta-1} = B(\alpha,\beta) = \frac{\Gamma(\alpha)\Gamma(\beta)}{\Gamma(\alpha+\beta)}

因此 (8)(8) 式成为：

∫ddlE(2π)d1(lE2+Δ)2=1(2π)d2πd/2Γ(d/2)⋅12(1Δ)2−d2Γ(d2)Γ(2−d2)Γ(2)=1(4π)d/2Γ(2−d2)Γ(2)(1Δ)2−d2(11)\begin{aligned} \int \frac{d^dl_E}{(2\pi)^d}\frac{1}{(l_E^2+\Delta)^2} &=\frac{1}{(2\pi)^d} \frac{2\pi^{d/2}}{\Gamma(d/2)}\cdot \frac{1}{2} (\frac{1}{\Delta})^{2-\frac{d}{2}} \frac{\Gamma(\frac{d}{2})\Gamma(2-\frac{d}{2})}{\Gamma(2)}\\ &= \frac{1}{(4\pi)^{d/2}}\frac{\Gamma(2-\frac{d}{2})}{\Gamma(2)}(\frac{1}{\Delta})^{2-\frac{d}{2}} \end{aligned}\tag{11}

考虑到 Γ(z)\Gamma(z) 在 z=0,−1,−2,⋯z = 0,-1,-2,\cdots 时存在孤立极点，这对应于 d=4,6,8,⋯d=4,6,8,\cdots。我们在考虑 d→4d\rightarrow 4 的行为时，我们可以令 ϵ=4−d\epsilon = 4-d，那么有如下近似：

Γ(2−d2)=Γ(ϵ2)=2ϵ−γ+O(ϵ)\Gamma(2-\frac{d}{2}) = \Gamma(\frac{\epsilon}{2}) = \frac{2}{\epsilon} - \gamma + \mathcal{O}(\epsilon)

其中 γ\gamma 为 Euler-Mascheroni 常数。那么 (11)(11) 式成为：

∫ddlE(2π)d1(lE2+Δ)2=1(4π)2Γ(ϵ2)(4πΔ)ϵ/2⟶ϵ→01(4π)2(2ϵ−γ+O(ϵ))(1+ϵ2log⁡4πΔ+O(ϵ))=1(4π)2(2ϵ−log⁡Δ−γ+log⁡(4π)+O(ϵ))\begin{aligned} \int \frac{d^dl_E}{(2\pi)^d}\frac{1}{(l_E^2+\Delta)^2} &= \frac{1}{(4\pi)^2}\Gamma(\frac{\epsilon}{2})(\frac{4\pi}{\Delta})^{\epsilon/2}\\ &\underset{\epsilon\rightarrow 0}{\longrightarrow}\frac{1}{(4\pi)^2}(\frac{2}{\epsilon} - \gamma + \mathcal{O}(\epsilon))(1 + \frac{\epsilon}{2} \log \frac{4\pi}{\Delta} + \mathcal{O}(\epsilon))\\ &= \frac{1}{(4\pi)^2}(\frac{2}{\epsilon} -\log\Delta - \gamma + \log (4\pi) + \mathcal{O}(\epsilon)) \end{aligned}

根据 Pauli-Villars 正规化方式，我们将得到的结果为：

∫d4lE(2π)41(lE2+Δ)2⟶Λ→∞1(4π)2(log⁡xΛ2Δ+O(Λ−1))\int \frac{d^4 l_E}{(2\pi)^4}\frac{1}{(l_E^2+\Delta)^2} \underset{\Lambda \rightarrow \infty}{\longrightarrow} \frac{1}{(4\pi)^2}(\log \frac{x\Lambda^2}{\Delta} + \mathcal{O}(\Lambda^{-1}))

我们容易推广以上结果，得到其他的积分公式：

∫ddlE(2π)d1(lE2+Δ)n=1(4π)d/2Γ(n−d2)Γ(n)(1Δ)n−d2∫ddlE(2π)dlE2(lE2+Δ)n=1(4π)d/2d2Γ(n−d2−1)Γ(n)(1Δ)n−d2−1\begin{aligned} \int \frac{d^dl_E}{(2\pi)^d}\frac{1}{(l_E^2+\Delta)^n} &= \frac{1}{(4\pi)^{d/2}}\frac{\Gamma(n-\frac{d}{2})}{\Gamma(n)}(\frac{1}{\Delta})^{n-\frac{d}{2}}\\ \int \frac{d^dl_E}{(2\pi)^d}\frac{l_E^2}{(l_E^2+\Delta)^n} &= \frac{1}{(4\pi)^{d/2}}\frac{d}{2}\frac{\Gamma(n-\frac{d}{2}-1)}{\Gamma(n)}(\frac{1}{\Delta})^{n-\frac{d}{2}-1}\\ \end{aligned}

在 dd 维时空中有：

gμνgμν=dg^{\mu\nu}g_{\mu\nu} = d

因此对于包含 lμlνl^{\mu}l^{\nu}，我们需要替换为：

lμlν→1dl2gμνl^{\mu}l^{\nu} \rightarrow \frac{1}{d}l^2g^{\mu\nu}

对于 Dirac 矩阵来说，以下式子仍然成立：

{γμ,γν},tr[1]=4\{\gamma^{\mu},\gamma^{\nu}\},\quad \mathrm{tr}[1] = 4

但有些结果需要进行修改：

γμγνγμ=−(2−ϵ)γνγμγνγργμ=4gνρ−ϵγνγργμγνγργσγμ=−2γσγργν+ϵγνγργσ\begin{aligned} \gamma^{\mu}\gamma^{\nu}\gamma_{\mu} &= -(2-\epsilon)\gamma^{\nu}\\ \gamma^{\mu}\gamma^{\nu}\gamma^{\rho}\gamma_{\mu} &= 4g^{\nu\rho} - \epsilon\gamma^{\nu}\gamma^{\rho}\\ \gamma^{\mu}\gamma^{\nu}\gamma^{\rho}\gamma^{\sigma}\gamma_{\mu} &= -2\gamma^{\sigma}\gamma^{\rho}\gamma^{\nu} + \epsilon\gamma^{\nu}\gamma^{\rho}\gamma^{\sigma}\\ \end{aligned}

使用维度正规化计算 Π2\Pi_2

现在使用维度正规化的方式计算 Π2\Pi_2。

根据上述介绍的积分公式，其中有关 l2l^2 的项成为：

∫ddlE(2π)d(−2d+1)gμνlE2(lE2+Δ)2=−1(4π)d/2(1−d2)Γ(1−d2)(1Δ)1−d2gμν=1(4π)d/2Γ(2−d2)(1Δ)2−d2(−Δgμν)\begin{aligned} \int \frac{d^dl_E}{(2\pi)^d}\frac{(-\frac{2}{d}+1)g^{\mu\nu}l_E^2}{(l_E^2+\Delta)^2} &= -\frac{1}{(4\pi)^{d/2}}(1-\frac{d}{2})\Gamma(1-\frac{d}{2})(\frac{1}{\Delta})^{1-\frac{d}{2}}g^{\mu\nu}\\ &= \frac{1}{(4\pi)^{d/2}}\Gamma(2-\frac{d}{2})(\frac{1}{\Delta})^{2-\frac{d}{2}}(-\Delta g^{\mu\nu})\\ \end{aligned}

因此上式在 d=2d=2 时并无极点。

现在我们继续计算 Π2μν\Pi_2^{\mu\nu}：

iΠ2μν(q)=−4ie2∫01dx1(4π)d/2Γ(2−d2)Δ2−d/2⋅(−Δgμν−2x(1−x)qμqν+gμν(m2+x(1−x)q2))=−4ie2∫01dx1(4π)d/2Γ(2−d2)Δ2−d/2⋅2x(1−x)(q2gμν−qμqν)=(q2gμν−qμqν)⋅iΠ2(q2)\begin{aligned} i\Pi_2^{\mu\nu}(q) &= -4ie^2\int_{0}^{1}dx \frac{1}{(4\pi)^{d/2}} \frac{\Gamma(2-\frac{d}{2})}{\Delta^{2-d/2}}\\ &\quad\cdot (-\Delta g^{\mu\nu} - 2x(1-x)q^{\mu}q^{\nu} + g^{\mu\nu}(m^2+x(1-x)q^2))\\ &= -4ie^2\int_{0}^{1}dx \frac{1}{(4\pi)^{d/2}} \frac{\Gamma(2-\frac{d}{2})}{\Delta^{2-d/2}}\cdot 2x(1-x)(q^2g^{\mu\nu}-q^{\mu}q^{\nu})\\ &= (q^2g^{\mu\nu}-q^{\mu}q^{\nu})\cdot i\Pi_2(q^2)\\ \end{aligned}

其中：

Π2(q2)=−8e2(4π)d/2∫01dxx(1−x)Γ(2−d2)Δ2−d/2⟶d→4−8e2(4π)2∫01dxx(1−x)(2ϵ−log⁡Δ−γ+log⁡(4π))=−2απ∫01dxx(1−x)(2ϵ−log⁡Δ−γ+log⁡(4π))\begin{aligned} \Pi_2(q^2) &= \frac{-8e^2}{(4\pi)^{d/2}}\int_{0}^{1}dx x(1-x) \frac{\Gamma(2-\frac{d}{2})}{\Delta^{2-d/2}}\\ &\underset{d\rightarrow 4}{\longrightarrow} \frac{-8e^2}{(4\pi)^2} \int_{0}^{1}dxx(1-x)(\frac{2}{\epsilon} -\log\Delta - \gamma + \log (4\pi))\\ &= -\frac{2\alpha}{\pi} \int_{0}^{1}dx x(1-x)(\frac{2}{\epsilon} -\log\Delta - \gamma + \log (4\pi))\\ \end{aligned}

如此，我们可以得到 O(α)\mathcal{O}(\alpha) 阶的电子电荷量修正：

e2−e02e02=δZ3=O(α)Π2(0)≈−2α3πϵ\frac{e^2-e_0^2}{e^2_0} = \delta Z_3 \underset{\mathcal{O}(\alpha)}{=}\Pi_2(0) \approx -\frac{2\alpha}{3\pi\epsilon}

尽管该项修正是无穷大的，但确实不可观测的。我们可以观测的是其对 q2q^2 的依赖关系，即下列物理量：

Π^2(q2)=Π2(q2)−Π2(0)=−2απ∫01dxx(1−x)log⁡(m2m2−x(1−x)q2)(12)\begin{aligned} \hat{\Pi}_2(q^2) &= \Pi_2(q^2) - \Pi_2(0)\\ &= -\frac{2\alpha}{\pi} \int_{0}^{1}dx x(1-x)\log(\frac{m^2}{m^2-x(1-x)q^2}) \end{aligned}\tag{12}

Π2\Pi_2 的分析

我们来分析以上结果，当 q2>0q^2>0 时，对应 ss-channel，考虑 m2−x(1−x)q2m^2-x(1-x)q^2 在 x=12x=\frac{1}{2} 时取最小值：

m2−14q2m^2 -\frac{1}{4}q^2

因此在 q2=4m2q^2 = 4m^2 时，Π^2(q2)\hat{\Pi}_2(q^2) 开始出现 branch cut。这正对应于产生两个实的正负电子对。

现在我们来计算 q2>4m2q^2>4m^2 时，Π^2\hat{\Pi}_2 的虚部。对虚部有贡献的区间为：

x∈(12−12β,12+12β),β=1−4m2q2x\in(\frac{1}{2}-\frac{1}{2}\beta,\frac{1}{2}+\frac{1}{2}\beta),\quad \beta = \sqrt{1-\frac{4m^2}{q^2}}

因此有：

Im[Π^2(q2±iϵ)]=−2απ∫12−12β12+12βdxx(1−x)Im(−log⁡(m2−x(1−x)(q2±iϵ)))=−2απ(±π)∫12−12β12+12βdxx(1−x)=∓α31−4m2q2(1+2m2q2)\begin{aligned} \mathrm{Im}[\hat{\Pi}_2(q^2\pm i\epsilon)] &= -\frac{2\alpha}{\pi}\int_{\frac{1}{2}-\frac{1}{2}\beta}^{\frac{1}{2}+\frac{1}{2}\beta} dx x(1-x)\mathrm{Im}(-\log(m^2-x(1-x)(q^2\pm i\epsilon)))\\ &= -\frac{2\alpha}{\pi}(\pm \pi)\int_{\frac{1}{2}-\frac{1}{2}\beta}^{\frac{1}{2}+\frac{1}{2}\beta} dx x(1-x)\\ &= \mp \frac{\alpha}{3}\sqrt{1-\frac{4m^2}{q^2}}(1+\frac{2m^2}{q^2})\\ \end{aligned}

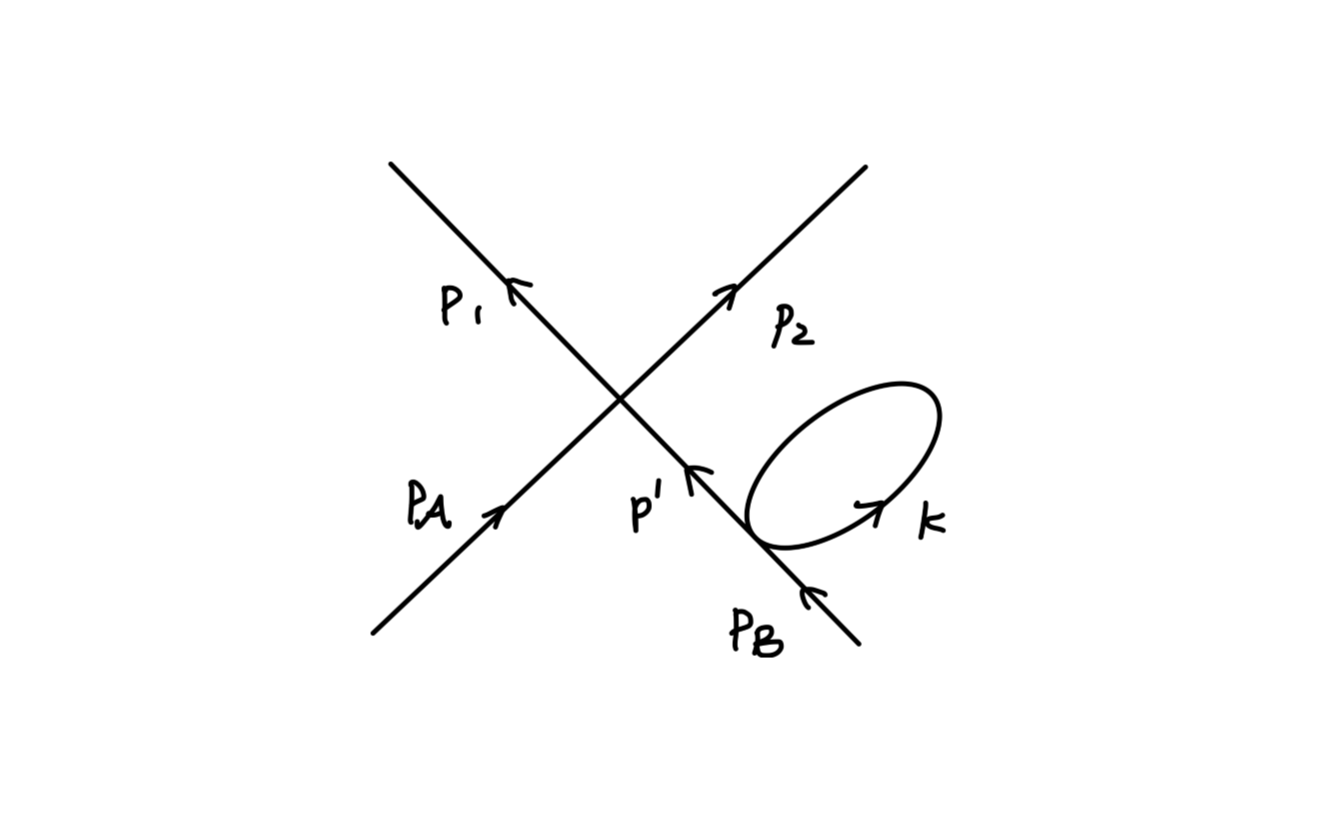
该表达式对 q2q^2 的依赖关系和我们之前介绍的 e+e−→ffˉe^{+}e^{-} \rightarrow f\bar{f} 过程类似。这正是由于光学定理，如下图：

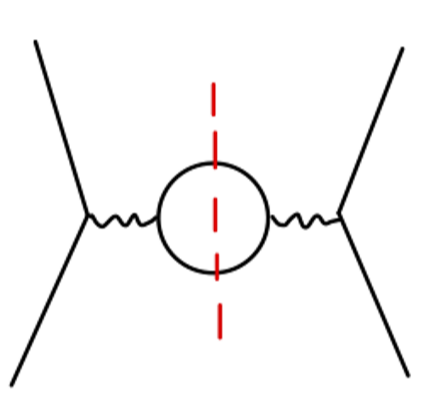
我们现在来看看 Π^2(q2)\hat{\Pi}_2(q^2) 如何影响电磁相互作用。

我们可以将静电势写为如下形式：

V(x)=ie2(2π)2r∫−∞∞dQQeiQrQ2+μ2[1+Π^2(−Q2)](13)V(\bm{x}) = \frac{ie^2}{(2\pi)^2r}\int_{-\infty}^{\infty}dQ \frac{Qe^{iQr}}{Q^2+\mu^2}[1+\hat{\Pi}_2(-Q^2)]\tag{13}

注意这里我们为光子引入了一个小质量 μ\mu。

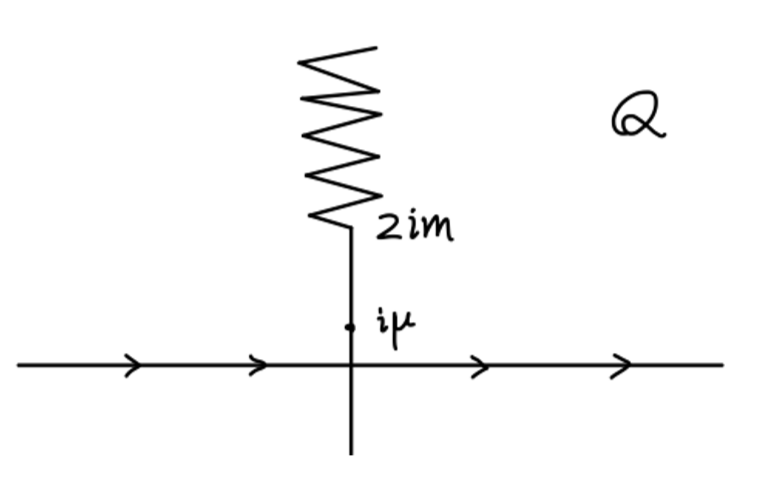
我们选取积分围线向上闭合。领头阶贡献来自于极点 Q=iμQ = i\mu，这将给出库伦势：

V=αrV = \frac{\alpha}{r}

但是仍然存在来自于 branch cut 的额外贡献。branch cut 开始于 Q=2miQ = 2mi。Π2\Pi_2 的实部是连续的，额外贡献来自于虚部的不连续性，定义 q=−iQq=-iQ：

δV(r)=−e2(2π)2r⋅2∫2m∞dqe−qrqIm[Π^2(q2−iϵ)]=−αr2π⋅∫2m∞dqe−qrqα31−4m2q2(1+2m2q2)(14)\begin{aligned} \delta V(r) &= \frac{-e^2}{(2\pi)^2r}\cdot 2\int_{2m}^{\infty}dq\frac{e^{-qr}}{q}\mathrm{Im}[\hat{\Pi}_2(q^2-i\epsilon)]\\ &= -\frac{\alpha}{r}\frac{2}{\pi}\cdot\int_{2m}^{\infty}dq\frac{e^{-qr}}{q}\frac{\alpha}{3}\sqrt{1-\frac{4m^2}{q^2}}(1+\frac{2m^2}{q^2}) \end{aligned}\tag{14}

当 r≫1/mr \gg 1/m 时，该积分主要由 q≈2mq\approx 2m 的区域贡献。做代换 t=q−2mt = q-2m，可以近似得到：

δV(r)≈−αr2π⋅∫0∞dte−(t+2m)r2mα3tm(32)=−αr⋅α4πe−2mr(mr)3/2(15)\begin{aligned} \delta V(r) &\approx -\frac{\alpha}{r}\frac{2}{\pi}\cdot\int_{0}^{\infty}dt \frac{e^{-(t+2m)r}}{2m}\frac{\alpha}{3}\sqrt{\frac{t}{m}}(\frac{3}{2})\\ &=-\frac{\alpha}{r}\cdot\frac{\alpha}{4\sqrt{\pi}}\frac{e^{-2mr}}{(mr)^{3/2}} \tag{15} \end{aligned}

因此可以得到库伦势为：

V(r)=αr(1+α4πe−2mr(mr)3/2+⋯ )(16)V(r) = \frac{\alpha}{r}(1 + \frac{\alpha}{4\sqrt{\pi}}\frac{e^{-2mr}}{(mr)^{3/2}} + \cdots) \tag{16}

对库伦势的辐射修正称为 Uehling potential。

另一方面，我们可以考虑 −q2≫m2-q^2 \gg m^2 的情况，此时 Π^2\hat{\Pi}_2 成为：

Π^2(q2)≈2απ∫01dxx(1−x)(log⁡(−q2m2)+log⁡(x(1−x))+O(m2q2))=α3π[log⁡(−q2m2)−53+O(m2q2)]\begin{aligned} \hat{\Pi}_2(q^2) &\approx \frac{2\alpha}{\pi}\int_{0}^{1}dxx(1-x)(\log(-\frac{q^2}{m^2}) + \log(x(1-x)) + \mathcal{O}(\frac{m^2}{q^2}))\\ &= \frac{\alpha}{3\pi}[\log(-\frac{q^2}{m^2}) -\frac{5}{3} + \mathcal{O}(\frac{m^2}{q^2})] \end{aligned}

因此有效耦合常数在此极限下成为：

αeff(q2)=α1−α3πlog⁡(−q2Am2)\alpha_{eff}(q^2) = \frac{\alpha}{1-\frac{\alpha}{3\pi}\log(-\frac{q^2}{Am^2})}

其中 A=exp⁡(5/3)A = \exp(5/3)。