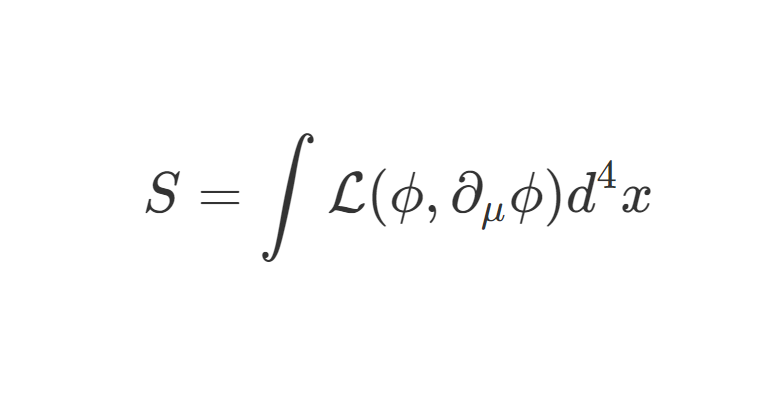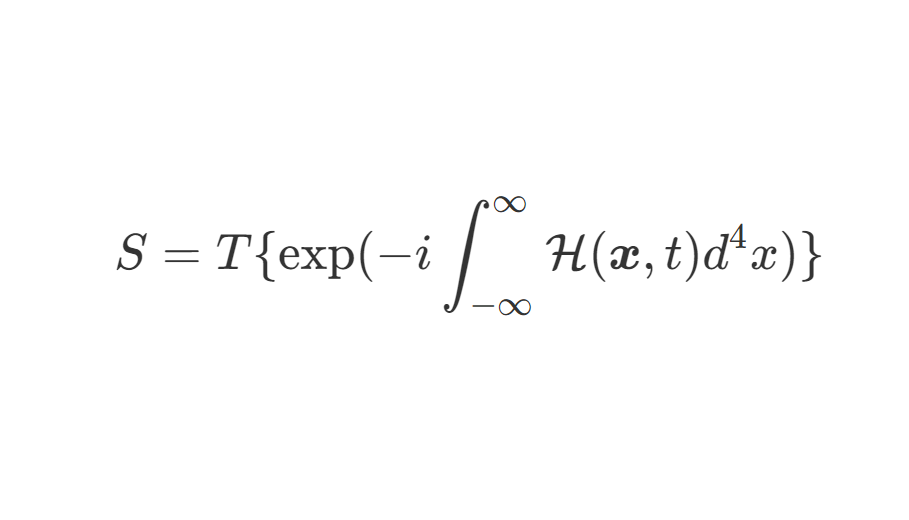量子力学的路径积分表述
量子力学和量子场论的 路径积分表述 path integral formulation/functional integral 是一个从经典力学里的最小作用量原理延伸出来的对量子物理的一种概括和公式化的方法
我们现在首先对于最简单的问题——应用路径积分表述讨论一维非相对论性粒子的运动。该粒子的哈密顿量为:
H=2mp2+V(x)(1)
现在考虑该粒子在时间 T 内从 xa 到 xb 的跃迁几率幅:
U(xa,xb;T)=⟨xa∣e−iHT/ℏ∣xb⟩(2)
另一方面来看,量子力学告诉我们:T 时间内从 xa 到 xb 的每一条路径都应当对该跃迁几率幅有贡献:
U(xa,xb;T)=all paths∑ei⋅(phase)=∫Dx(t)ei⋅(phase)
这里 ∫Dx(t) 表示对所有可能路径的求和。上述的相位是一个关于路径 x(t) 的泛函。那么这个相位是什么呢?最小作用量原理启发我们:当量子力学过渡到经典力学后,真实路径应当对应于作用量取极小值的路径,我们记为 xcl:
δx(t)δ(S[x(t)])∣xc1=0
具有如此稳定性的路径也应当对跃迁几率幅具有最大的贡献。我们可以取该相位就为作用量 S[x(t)]/ℏ,那么有:
U(xa,xb;T)=∫Dx(t)eiS[x(t)]/ℏ(3)
现在我们尝试对该路径积分进行计算。第一次接触路径积分,我们先使用一种容易理解的方式进行计算。
我们将路径 x(t) 分为一段一段的时间切片,每一小段的时间间隔为 ϵ。在每一个时间切片中,我们可以假设粒子以匀速直线运动,这样我们就把路径 x(t) 分解成了一段段时间内的匀速直线运动。
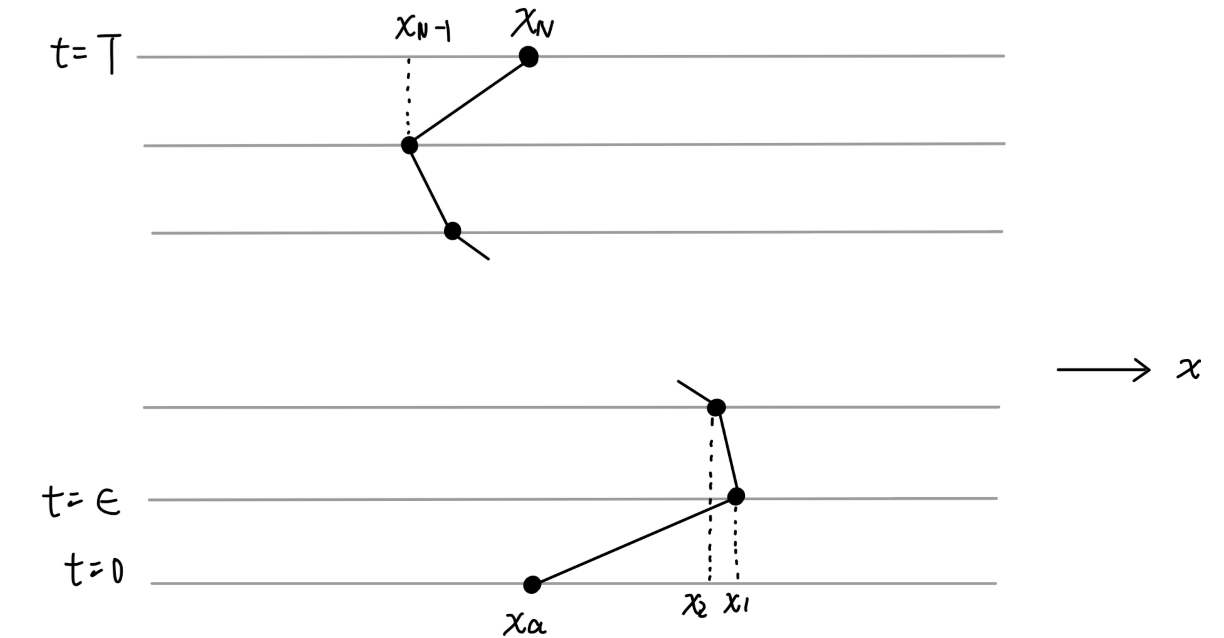
那么作用量成为:
S=∫0Tdt(2mx˙2−V(x))→k∑(2mϵ(xk+1−xk)2−ϵV(2xk+1+xk))(4)
对所有路径的积分成为:
∫Dx(t)→∫C(ϵ)dx1∫C(ϵ)dx2⋯∫C(ϵ)dxNδ(i=1∑Nxi−(xb−xa))=C(ϵ)1∫C(ϵ)dx1∫C(ϵ)dx2⋯∫C(ϵ)dxN−1=C(ϵ)1k∏∫−∞∞C(ϵ)dxk(5)
其中 C(ϵ) 是一个取决于 ϵ 的常数。
我们现在来推导 U(xa,xb;T) 的运动方程。考虑相邻时间切片上的跃迁几率幅的关系,有:
U(xa,xb;T)=∫Dx(t)eiS[x(t)]/ℏ=C(ϵ)1∫C(ϵ)dx1∫C(ϵ)dx2⋯∫C(ϵ)dxN−1eiS[x(t)]/ℏ=∫−∞∞C(ϵ)dx′exp[ℏi2ϵm(xb−x′)2−ℏiϵV(2xb+x′)]U(xa,x′;T−ϵ)=∫−∞∞C(ϵ)dx′exp[ℏi2ϵm(xb−x′)2][1−ℏiϵV(xb)+⋯]×[1+(x′−xb)∂xb∂+21(x′−xb)2∂xb2∂2+⋯]U(xa,xb;T−ϵ)
利用高斯积分公式:
∫dξe−bξ2=bπ∫dξξe−bξ2=0∫dξξ2e−bξ2=2b1bπ
得到:
U(xa,xb;T)=(C1−im2πℏϵ)(1−ℏiϵV(xb)+2miϵℏ∂xb2∂2+O(ϵ2))U(xa,xb;T−ϵ)(6)
考虑到 ϵ→0 时,应当有:
U(xa,xb;T−ϵ)→U(xa,xb;T)
那么可以取:
C(ϵ)=−im2πℏϵ(7)
忽略有关 ϵ 的高阶项,(6) 式成为:
U(xa,xb;T)=(1−ℏiϵV(xb)+2miϵℏ∂xb2∂2)U(xa,xb;T−ϵ)(8)
得到:
iℏϵU(xa,xb;T)−U(xa,xb;T−ϵ)=(V(xb)−2mℏ2∂xb2∂2)U(xa,xb;T)
令 ϵ→0,即得到:
iℏ∂t∂U(xa,xb;T)=(V(xb)−2mℏ2∂xb2∂2)U(xa,xb;T)=HU(xa,xb;T)(9)
这不是别的,正是薛定谔方程,这验证我们路径积分表述的合理性。
现在我们想把我们得到的路径积分表述推广到更一般的情形。不妨用一组坐标 qi,动量 pi 来表示系统的位形。
我们现在来计算如下跃迁几率幅:
U(xa,xb;T)=⟨qb∣e−iHT∣qa⟩
我们想要直接证明上述表达式与路径积分表述是相同的。同样对时间进行切片,每个时间切片的时间间隔为 ϵ。那么有:
e−iHT=N factorse−iHϵe−iHϵ⋯e−iHϵ
我们现在插入如下恒等算子:
1=(i∏∫dqki)∣qk⟩⟨qk∣(10)
对于每一个时间切片来说,其形式为:
⟨qk+1∣e−iHϵ∣qk⟩ϵ→0⟶⟨qk+1∣1−iHϵ+⋯∣qk⟩
其中取 q0=qa,qN=qb。哈密顿量是 p,q 的函数:
H=H(p,q)
我们首先考虑几种简单情况:
⟨qk+1∣f(q)∣qk⟩⟨qk+1∣f(p)∣qk⟩=f(qk)i∏δ(qk+1i−qk+1i)=f(2qk+qk+1)(i∏∫2πdpki)exp[ii∑pki(qk+1i−qki)]=(i∏∫2πdpki)f(pk)exp[ii∑pki(qk+1i−qki)]
若 H 仅含有 f(p),f(q) 形式的项,那么以上公式可统一写为:
⟨qk+1∣H(p,q)∣qk⟩=(i∏∫2πdpki)H(qk,pk)exp[ii∑pki(qk+1i−qki)](11)
对于一般的 H(p,q),上述公式是不成立的。不过存在以下情况:
⟨qk+1∣41(q2p2+2qp2q+p2q2)∣qk⟩=(2qk+qk+1)2⟨qk+1∣p2∣qk⟩=(i∏∫2πdpki)H(qk,pk)exp[ii∑pki(qk+1i−qki)]
此时,H(p,q) 被称为 Wely-ordered。任何一个哈密顿量都可以通过交换 p,q 成为 Wely-ordered。因此我们现在开始,不妨假设哈密顿量是 Wely-ordered 的,那么 (11) 式总成立。如此,我们得到:
⟨qk+1∣e−iϵH∣qk⟩=(i∏∫2πdpki)exp[−iϵH(2qk+1+qk,pk)]exp[ii∑pki(qk+1i−qki)]
由此得到:
U(q0,qN;T)=⟨q0∣e−iHT∣qN⟩=i,k∏∫dqki⟨qk∣e−iϵH∣qk+1⟩=(i,k∏∫dqki∫2πdpki)exp[ik∑(i∑pki(qk+1i−qki)−ϵH(2qk+1+qk,pk))]
写为泛函积分的形式:
U(q0,qN;T)=(i∏∫Dq(t)Dp(t))exp[i∫0Tdt(i∑piq˙i−H(q,p))](12)
这里的积分测度等价于经典表述中对相空间的积分:
i∏∫2πℏdqidpi
标量场的量子化
现在我们尝试使用路径积分方法对标量场进行量子化。考虑标量场的哈密顿量为:
H=∫d3x[21π2+21(∇ϕ)2+V(ϕ)](13)
根据 (12) 式得到其跃迁几率幅:
⟨ϕb(x)∣e−iHT∣ϕa(x)⟩=∫DϕDπexp[i∫0Td4x(πϕ˙−21π2−21(∇ϕ)2−V(ϕ))]=∫Dϕexp[i∫0Td4x(21(∂μϕ)2−V(ϕ))](14)
两点关联函数
现在来计算关联函数。不妨考虑如下表达式:
∫Dϕ(x)ϕ(x1)ϕ(x2)exp[i∫−TTd4xL(ϕ)](15)
并给定边界条件:
ϕ(−T,x)=ϕa(x),ϕ(T,x)=ϕb(x)
我们现在想要做的事情是:把它同如下的两点关联函数关联起来:
⟨Ω∣TϕH(x1)ϕH(x2)∣Ω⟩
考虑到泛函积分可以写为:
∫Dϕ(x)=∫Dϕ1(x)∫Dϕ2(x)∫ϕ(x1,20,x)=ϕ1,2(x)Dϕ(x)(16)
其中最后一个积分的含义为:在固定时间 x10 与 x20,ϕ(x10,x) 与 ϕ(x20,x) 总分别取固定的值 ϕ1(x) 与 ϕ2(x)。如此 x10 与 x20 将 (−T,T) 分为三个时间段。不妨考虑 x10<x20,如此 (15) 式可以写为:
===∫Dϕ1(x)∫Dϕ2(x)ϕ1(x1)ϕ2(x2)∫ϕ(x1,20,x)=ϕ1,2(x)Dϕ(x)exp[i∫−TTd4xL(ϕ)]∫Dϕ1(x)∫Dϕ2(x)ϕ1(x1)ϕ2(x2)⟨ϕb∣e−iH(T−x20)∣ϕ2⟩⟨ϕ2∣e−iH(x20−x10)∣ϕ1⟩⟨ϕ1∣e−iH(x10+T)∣ϕa⟩⟨ϕb∣e−iH(T−x20)ϕS(x2)e−iH(x20−x10)ϕS(x1)e−iH(x10+T)∣ϕa⟩⟨Ω∣e−iHTϕH(x1)ϕH(x2)e−iHT∣Ω⟩
其中应用了 ϕS(x1)∣ϕ1⟩=ϕ1(x1)∣ϕ1⟩。那么对于 x10>x20 的情况,同理得到其结果为:
⟨Ω∣e−iHTϕH(x2)ϕH(x1)e−iHT∣Ω⟩
如此,我们最终得到:
∫Dϕ(x)ϕ(x1)ϕ(x2)exp[i∫−TTd4xL(ϕ)]=⟨Ω∣e−iHTT{ϕH(x1)ϕH(x2)}e−iHT∣Ω⟩
类似于之前的技巧,我们令 T→∞(1−iϵ),考虑到:
e−iHT∣ϕa⟩=n∑e−iEnT∣n⟩⟨n∣ϕa⟩T→∞(1−iϵ)⟶⟨Ω∣ϕa⟩e−iE0⋅∞(1−iϵ)∣Ω⟩
由此得到两点关联函数为:
⟨Ω∣TϕH(x1)ϕH(x2)∣Ω⟩=T→∞(1−iϵ)lim∫Dϕexp[i∫−TTd4xL]∫Dϕϕ(x1)ϕ(x2)exp[i∫−TTd4xL](17)
这就是两点关联函数的路径积分表述。
费曼规则
现在使用路径积分表述推导费曼规则。我们尝试直接计算两点关联函数 (17)。我们仍然采用“蛮力”,从离散的情况逐渐过渡到连续的泛函积分。
那么,我们首先在离散的四维格子上定义标量场 ϕ(xi),设格距为 ϵ,那么可以定义:
ϕ=i∏dϕ(xi)
通过傅里叶变换,可以将场量在动量空间中表示为:
ϕ(xi)=V1n∑e−ikn⋅xiϕ(kn)
其中 ϕ 为实值场要求:
ϕ(kn)=ϕ∗(−kn)
因此,我们可以选取 kn0>0 部分的实部与虚部作为独立变量。因此有:
Dϕ(x)=kn0>0∏dReϕ(kn)dImϕ(kn)
过渡到连续极限时,有 ϵ→0,V→∞,如此等价于以下替代:
V1n∑→∫(2π)4d4k
现在,我们可以对离散情形写出作用量:
S0=∫d4x[21(∂μϕ)2−21m2ϕ2]=−∫d4x∫(2π)8d4kd4k′21(m2−kk′)ϕ(k)ϕ∗(k′)e−i(k−k′)⋅x=−∫(2π)8d4kd4k′21(m2−kk′)ϕ(k)ϕ∗(k′)(2π)4δ(k−k′)=−∫(2π)4d4k21(m2−k2)ϕ(k)ϕ∗(k)→−V1n∑21(m2−kn2)∣ϕ(kn)∣2=−V1kn0>0∑(m2−kn2)((Reϕn)2+(Imϕn)2)
如此得到:
∫DϕeiS0=(kn0>0∏∫dReϕ(kn)dImϕ(kn))exp(−Vikn0>0∑(m2−kn2)((Reϕn)2+(Imϕn)2))=kn0>0∏(∫dReϕnexp(−Vikn0>0∑(m2−kn2)Reϕn2)(∫dImϕnexp(−Vikn0>0∑(m2−kn2)Imϕn2)=kn0>0∏m2−kn2−iπVm2−kn2−iπV=kn∏m2−kn2−iπV
这个结果是需要修正的,因为考虑到直线我们对时间的积分是沿着轴 t→t(1−iϵ),因此对应的,我们需要将对 k0 的积分修改为:k0→k0(1+iϵ),这等价于做如下替换:
(k2−m2)→(k2−m2+iϵ)
为了理解上述结果,我们进行一个类比,考虑如下式子:
(k∏∫dξk)exp[−ξiBijξj]
设有正交变换 ξi=Oijxj 使 Bij 对角化,有:
(k∏∫dξk)exp[−ξiBijξj]=(k∏∫dxk)exp[−i∑bixi2]=i∏(∫dxiexp[−bixi2])=i∏biπ=const ×[detB]−1/2
现在我们将作用量通过分部积分写为以下形式:
S0=21∫d4xϕ(−∂2−m2)ϕ+(surface term)
那我们可以形式上得到下列式子:
∫DϕeiS0=const ×[det(m2+∂2)]−1/2
其中包含的 det(m2+∂2) 为 泛函行列式 functional determinant。这个式子虽然看起来很病态,但是最终会消去。
现在我们继续计算两点关联函数的分子部分。
考虑到:
ϕ(x1)ϕ(x2)=V1m∑e−ikm⋅x1ϕmV1l∑e−ikl⋅x2ϕl
因此有:
∫Dϕϕ(x1)ϕ(x2)eiS0=V21m,l∑e−i(km⋅x1+kl⋅x2)(kn0>0∏∫dReϕndImϕn)×(Reϕm+iImϕm)(Reϕl+iImϕl)×exp(−Vikn0>0∑(m2−kn2)((Reϕn)2+(Imϕn)2))
对于大部分 km,kl 来说,上述表达式的值为零,因为得到的高斯积分是奇函数。只有对于少数特殊值才会有非零的结果。当 km=kl 时,(Reϕm)2 的贡献确实非零,但会同 (Imϕm)2 的项相抵消。我们考虑当 km=−kl 时,由 ϕ(−k)=ϕ(k)∗,可得 Imϕl=−Imϕm。那么这两项将相加,得到非零的贡献,即:
∫Dϕϕ(x1)ϕ(x2)eiS0=V21m∑e−ikm⋅(x1−x2)(kn0>0∏∫dReϕndImϕn)×(Reϕm+iImϕm)(Reϕm−iImϕm)×exp(−Vikn0>0∑(m2−kn2)((Reϕn)2+(Imϕn)2))=V21m∑e−ikm⋅(x1−x2)(kn0>0,n=m∏∫dReϕnexp(−Vikn0>0∑(m2−kn2)Reϕn2)×∫dImϕnexp(−Vikn0>0∑(m2−kn2)Imϕn2))×2∫dReϕm(Reϕm)2exp(−Vikn0>0∑(m2−km2)Reϕm2)×∫dImϕmexp(−Vikn0>0∑(m2−km2)Imϕm2)=V21m∑e−ikm⋅(x1−x2)(kn0>0,n=m∏m2−kn2−iπV)⋅m2−km2−iπV⋅m2−km2−iϵ−iV=V21m∑e−ikm⋅(x1−x2)(kn0>0∏m2−kn2−iπV)m2−km2−iϵ−iV=(kn∏m2−kn2−iπV)×V1m∑e−ikm⋅(x1−x2)km2−m2+iϵi
取连续极限得到:
⟨0∣Tϕ(x1)ϕ(x2)∣0⟩=V1m∑e−ikm⋅(x1−x2)km2−m2+iϵi→∫(2π)4d4kk2−m2+iϵie−ik⋅(x1−x2)=DF(x1−x2)(18)
在这里,我们使用路径积分方法计算了标量场的两点关联函数,同理我们可以使用这种方法计算更高阶的关联函数,不过这种方法比较繁琐,我们之后会介绍一种更为简单的方法进行计算。
当需要考虑微扰进行微扰论的计算时,例如 ϕ4 理论,我们只需要考虑进行如下展开即可:
exp[i∫d4xL]=exp[i∫d4xL0](1−i∫d4x4!λϕ4+⋯)
泛函导数与生成泛函
现在,我们介绍一种更为常用的方法。我们首先引入泛函导数:δ/δJ(x),具有如下基本形式:
δJ(x)δJ(y)=δ(4)(x−y)(19)
写为积分形式:
δJ(x)δ∫d4yJ(y)ϕ(y)=ϕ(x)(20)
利用泛函导数,我们可以得到以下表达式:
δJ(x)δexp[i∫d4yJ(y)ϕ(y)]=iϕ(x)exp[i∫d4yJ(y)ϕ(y)](21)
由以上性质,我们可以定义如下标量场的 生成泛函 generating functional Z[J]:
Z[J]≡∫Dϕexp[i∫d4y[L+J(y)ϕ(y)]](22)
当 J=0 时,有:
Z0=Z[0]=∫Dϕexp[i∫d4yL](23)
如此,利用生成泛函与泛函导数,两点关联函数可以写为:
⟨0∣Tϕ(x1)ϕ(x2)∣0⟩=∫Dϕexp[i∫d4yL]∫Dϕϕ(x1)ϕ(x2)exp[i∫d4yL]=Z01(−iδJ(x1)δ)(−iδJ(x2)δ)Z[J]∣J=0
以 Klein-Gordon 场为例,有:
∫d4x(L0(ϕ)+Jϕ)=∫d4x(21ϕ(−∂2−m2+iϵ)ϕ+Jϕ)(24)
我们对 ϕ 作一个 shift,进行如下代换:
ϕ′(x)=ϕ(x)−i∫d4yDF(x−y)J(y)(25)
代入 (24) 式中得到:
∫d4x(L0(ϕ)+Jϕ)=∫d4x[21ϕ′(−∂2−m2+iϵ)ϕ′−21J(−∂2−m2+iϵ)−1J]
而本次 shift 的 Jacobi 行列式为 1,因此有:
Z[J]=∫Dϕ′exp[i∫d4xL0(ϕ′)]exp[−i∫d4xd4y21J(x)(−iDF(x−y))J(y)]=Z0exp[−∫d4xd4y21J(x)DF(x−y)J(y)]
这里仔细地对以上两式进行计算:
需要用到性质:Klein-Gordon 传播子 DF(x−y) 是 Klein-Gordon 方程的格林函数:
(∂2+m2)DF(x−y)=−iδ(4)(x−y)
=====∫d4x(L0(ϕ)+Jϕ)∫d4x(21ϕ(−∂2−m2+iϵ)ϕ+Jϕ)∫d4x21(ϕ′+i∫d4yDF(x−y)J(y))(−∂2−m2+iϵ)(ϕ′+i∫d4zDF(x−z)J(z))+J(ϕ′+i∫d4yDF(x−y)J(y)))∫d4x21ϕ′(−∂2−m2+iϵ)ϕ′+2i∫d4yDF(x−y)J(y)(−∂2−m2+iϵ)ϕ′(x)21(ϕ′+i∫d4yDF(x−y)J(y))(−i∫d4x(−i)δ(4)(x−z)J(z))+J(ϕ′+i∫d4yDF(x−y)J(y)))∫d4x21ϕ′(−∂2−m2+iϵ)ϕ′−21Jϕ′−21Jϕ′−2iJ∫d4yDF(x−y)+J(ϕ′+i∫d4yDF(x−y)J(y)))∫d4x[21ϕ′(−∂2−m2+iϵ)ϕ′−21J(−∂2−m2+iϵ)−1J]
其中求第五式第二项需要用到两次分部积分,且得到的两个表面项均为零,着等价于 Klein-Gorodn 算子向前作用。
如此两点关联函数成为:
⟨0∣Tϕ(x1)ϕ(x2)∣0⟩=−δJ(x1)δδJ(x2)δexp[−∫d4xd4y21J(x)DF(x−y)J(y)]∣J=0=−δJ(x1)δ[−21∫d4yDF(x2−y)J(y)−21∫d4xJ(x)DF(x−x2)]Z0Z[J]∣J=0=DF(x1−x2)
利用这种方法,能够更加方便地计算高阶关联函数。为了方便,我们采用如下的简写记号:
ϕ1≡ϕ(x1),Jx≡J(x),Dx4≡DF(x−x4)
并且用重复的下标代表积分。
那么有:
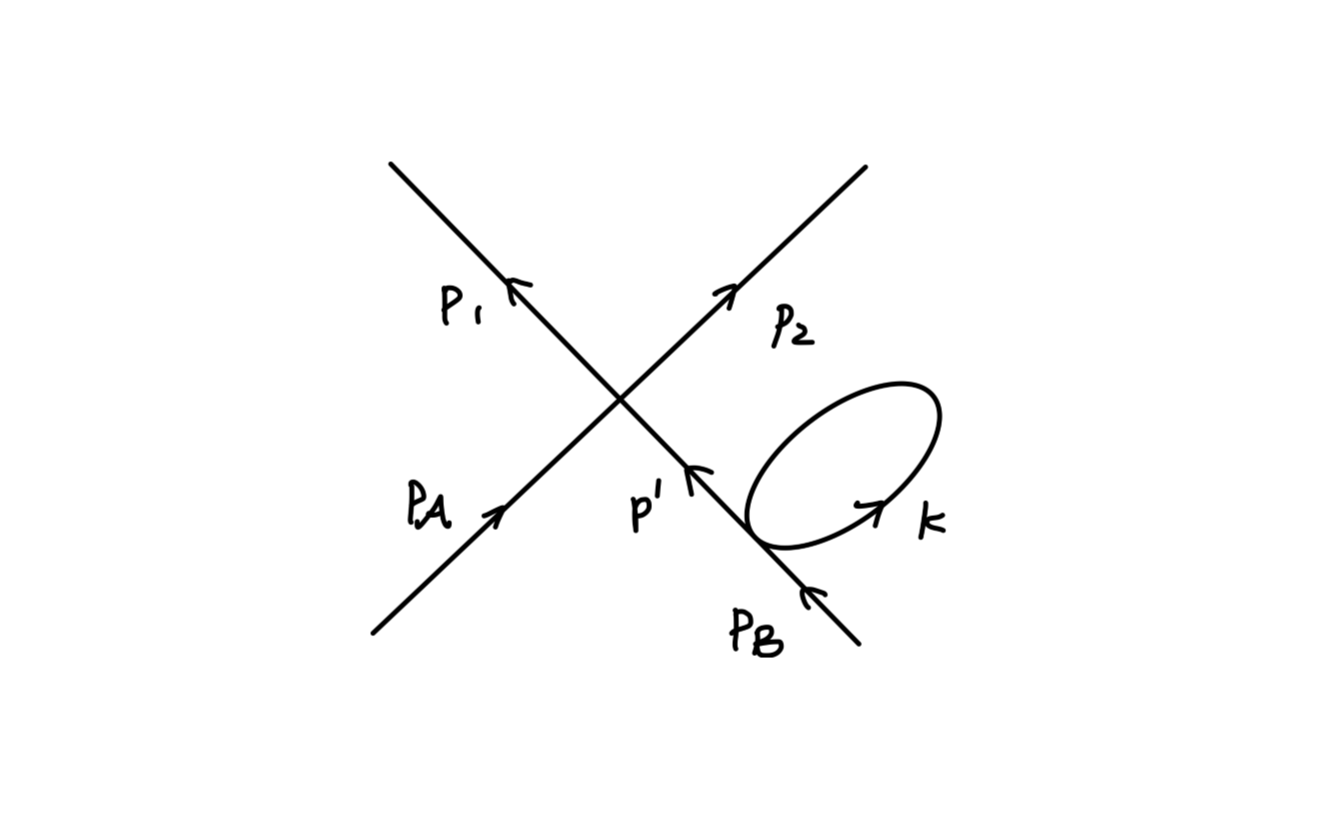
⟨0∣Tϕ1ϕ2ϕ3ϕ4∣0⟩=δJ1δδJ2δδJ3δδJ4δe−21JxDxyJy∣J=0=δJ1δδJ2δδJ3δ(−JxDx4)e−21JxDxyJy∣J=0=δJ1δδJ2δ(−D34+JxDx4JyDy3)e−21JxDxyJy∣J=0=δJ1δ(D34JxDx2+D24JyDy3+JxDx4D23)e−21JxDxyJy∣J=0=D34D12+D24D13+D14D23
这与我们之前得到的结果是一致的。