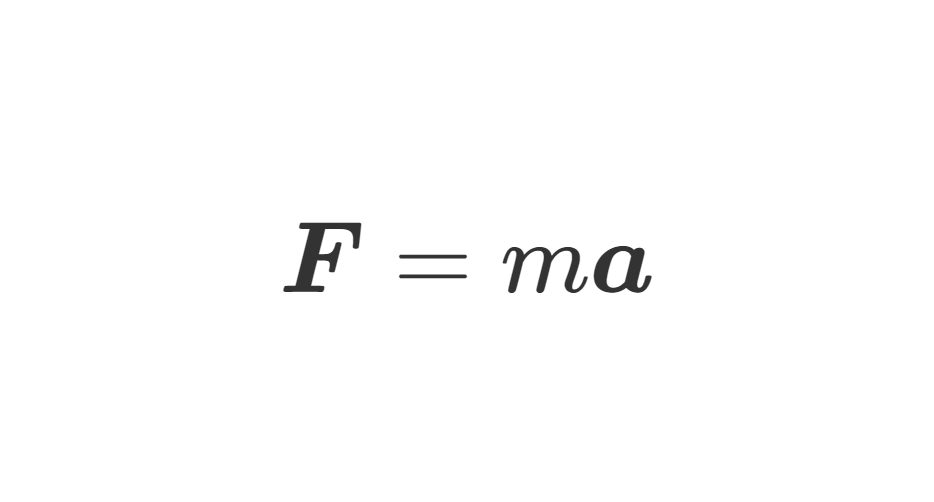前言：经典力学是学习近代物理的重要基础，它为近代物理提供了重要的理论背景，处理问题的基本框架。不同于牛顿对经典力学的矢量力学表述，分析力学用抽象的数学方法来诠释经典力学。出发点的不同使得它具有更大的普遍性，成为从经典力学到量子力学、统计力学的跳板。将矢量力学、分析力学等一系列经典力学的知识综合起来，于是成为理论力学这门学科。在本篇学习笔记中，我会介绍有关运动学的相关理论和一些重要的概念。当然，你需要提前掌握一些 微积分 、线性代数 与 普通物理 的知识。

牛顿创立经典力学时就采用了 矢量力学 的表述，他用了大量的矢量方法对经典力学问题进行描述分析：位移、速度、力、角动量等很多物理量都可以用一个矢量来描述，这样可以让我们对物理图像有着更直接的认识。接下来，我们从对一个质点运动的描述开始。

质点运动学

质点运动学研究单一质点的运动。

运动学的一些概念

质点：质点是一个有质量的点，在动力学中常用来代替物体。质点是一个物理抽象，也是一个理想化模型[1]^{[1]}。

在运动学中，我们忽略质点的质量属性而关注如何描述质点的 位置 、位置的变化快慢—— 速度、速度的变化快慢—— 加速度。

为了描述一个质点如何运动，我们首先需要一个观察者。这个观察者就成为了一个 参考系。在不同的参考系中，质点的运动状态可能不同。因此只有确定了一个参考系，才能对质点的运动状态进行描述。

参考系在物理学中是一个很重要的概念，我们将在后面进行更多解释。

运动的描述

确定了一个参考系后，可以用一个矢量来描述质点的 位置，位置矢量 常简称为 位矢。

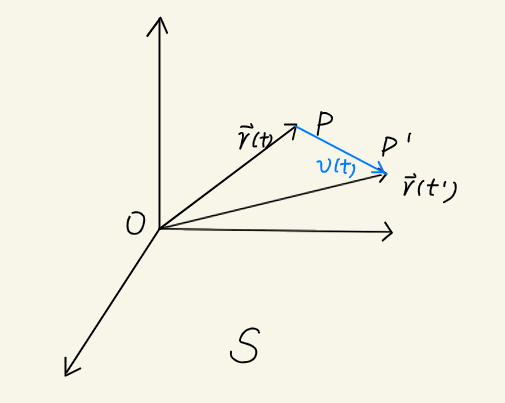
Fig1.1：位矢

如图1.1 ，在 参考系 SS 中，PP 为一个质点。矢量 r=OP\bm{r}=\bm{OP} 确定了该质点的位置。假设该质点在 t,t′t,t' 的位置分别为 r,r′\bm{r},\bm{r}'，那么这段时间中粒子的 平均速度 为：

vˉ=ΔrΔt\bar{\bm{v}}=\frac{\Delta \bm{r}}{\Delta t}

其中 Δr=r′−r\Delta \bm{r} =\bm{r}' - \bm{r} 为 位移，Δt=t′−t\Delta t =t'-t 为 时间间隔。

若把时间间隔取到很小，我们就可以用这段时间间隔内的平均速度来近似表示其中某一个时刻的速度。对应到极限情况，我们得到 瞬时速度：

v=lim⁡Δt→0ΔrΔt=drdt\bm{v} =\lim_{\Delta t\rightarrow 0} \frac{\Delta \bm{r}}{\Delta t}=\frac{d\bm{r}}{dt}

同理，加速度 描述速度的变化快慢。我们得到加速度的表达式：

a=dvdt=d2rdt2\bm{a} = \frac{d\bm{v}}{dt} = \frac{d^2\bm{r}}{dt^2}

在物理学中，我们常在物理量上加一点表示对时间的导数，因此速度和加速度也可以表示为:

v=r˙,a=r¨\bm{v}=\dot{\bm{r}},\quad \bm{a}=\ddot{\bm{r}}

运动的分量描述

对于一个特定的坐标系，可以通过相应坐标分量来描述质点的位置、速度、加速度。

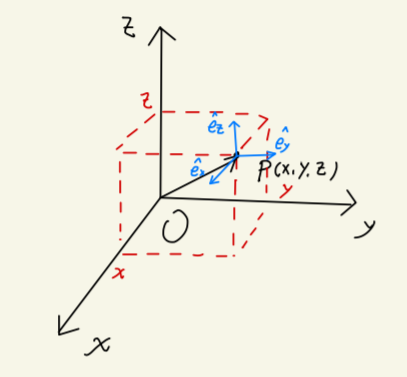
Fig1.2：直角坐标系

在直角坐标系中，质点的位置可以表示为 r=(x,y,z)\bm{r}=(x,y,z)。
若用 e^x,e^y,e^z\bm{\hat{e}}_x,\bm{\hat{e}}_y,\bm{\hat{e}}_z 来表示三个单位矢量，则有：

r=xe^x+ye^y+ze^z\bm{r}=x\bm{\hat{e}}_x+y\bm{\hat{e}}_y+z\bm{\hat{e}}_z

速度：

v=x˙e^x+y˙e^y+z˙e^z=vxe^x+vye^y+vze^z\begin{aligned} \bm{v}&=\dot{x}\bm{\hat{e}}_x+\dot{y}\bm{\hat{e}}_y+\dot{z}\bm{\hat{e}}_z\\ &=v_x\bm{\hat{e}}_x+v_y\bm{\hat{e}}_y+v_z\bm{\hat{e}}_z\\ \end{aligned}

加速度：

a=x¨e^x+y¨e^y+z¨e^z=axe^x+aye^y+aze^z\begin{aligned} \bm{a}&=\ddot{x}\bm{\hat{e}}_x+\ddot{y}\bm{\hat{e}}_y+\ddot{z}\bm{\hat{e}}_z\\ &=a_x\bm{\hat{e}}_x+a_y\bm{\hat{e}}_y+a_z\bm{\hat{e}}_z\\ \end{aligned}

在其他坐标系下，以下以 球坐标 与 柱坐标 为例，对应的表达式会复杂一些。这是因为在直角坐标系中，每个坐标基矢是不随质点的位置变化的。而在球坐标与柱坐标中，对应的基矢随位置变化，需要考虑对基矢部分的求导。

球坐标与柱坐标都引入了角位置进行描述，为了方便后面的讨论，我们有必要介绍以下质点的角坐标描述。

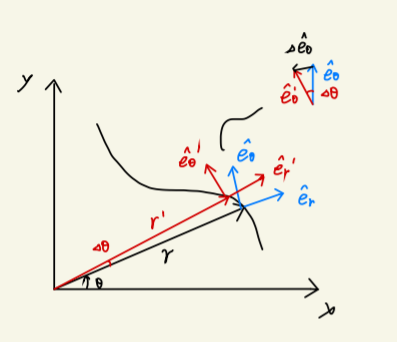
Fig1.3：角运动与基矢的变化

以平面极坐标系为例，有：
我们用 (r,θ)(r,\theta) 来描述位置。其中 θ\theta 就是一个角位置。方位角 θ\theta 的变化快慢定义 角速度：

ω=dθdt=θ˙\omega = \frac{d\theta}{dt}=\dot{\theta}

角速度的变化快慢定义为 角加速度：

β=dωdt=θ¨\beta = \frac{d\omega}{dt} = \ddot{\theta}

现在我们来考虑基矢的变化快慢，在一段时间间隔内，质点从 r=(r,θ)\bm{r}=(r,\theta) 运动到了 r′=(r′,θ′)\bm{r'}=(r',\theta')。对应的基矢成为 e^r′,e^θ′\bm{\hat{e}}'_r,\bm{\hat{e}}_\theta'。

我们分析基矢的变化快慢，可得：

de^rdt=−dθdte^r=−ωe^r\frac{d\bm{\hat{e}}_r}{dt}=-\frac{d\theta}{dt}\bm{\hat{e}}_r=-\omega\bm{\hat{e}}_r

推广到三维情况，我们用一个矢量表示角速度。

初学者可能会对角速度矢量感到诧异：为什么角位置是标量，而对角位置的求导得到的角速度却是矢量？这一点我们要回到如何给出角位置这个标量问题中来，在二维情况中，质点的运动被限制在一个平面内，因此得到一个角参量是容易的。然而在三维情况下，我们需要先找到一个平面，才能在这个平面中给出一个角参量。一个平面一个方向，也就是一个轴，角位置表示相对于这个轴的转动。如此，角速度矢量的定义就呼之欲出了：我们将这个轴定义为角速度矢量的方向（符合右手螺旋定则：右手四指沿角位置正方向转动，大拇指方向为角速度方向），大小为 dθ/dtd\theta/dt。

推广到三维，基矢对时间导数为：

de^rdt=ω×e^r\frac{d\bm{\hat{e}}_r}{dt}=\omega\times \bm{\hat{e}}_r

我们将在之后介绍这是如何推导的。

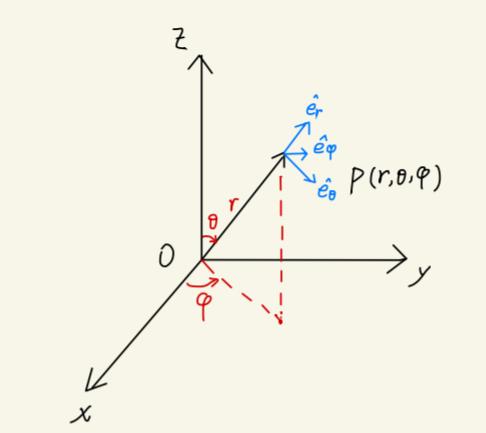
Fig1.4：球坐标系

在球坐标中，我们用 (r,θ,φ)(r,\theta,\varphi) 来描述质点位置。分别对应：径向距离、极角、方位角。需要注意的是，在数学中 θ,φ\theta,\varphi 的意义相反，这是因为在平面上，数学常用 θ\theta 表示方位角，而把 φ\varphi 看做方位角的三维推广。在物理学中，我们常用 (r,θ,φ)(r,\theta,\varphi) 的描述方式。

因此，质点位置为：

r=re^r\bm{r} = r\bm{\hat{e}}_r

角速度：

ω=φ˙e^z+θ˙e^φ\bm{\omega} = \dot{\varphi}\bm{\hat{e}}_z+\dot{\theta}\bm{\hat{e}}_\varphi

速度（以下方法可以推广到加速度的推导）：

v=r˙e^r+re^˙r=r˙e^r+rω×e^r=r˙e^r+r(φ˙e^z+θ˙e^φ)×e^r=r˙e^r+rθ˙e^θ+rφ˙sin⁡θe^φ\begin{aligned} \bm{v}=& \dot{r} \bm{\hat{e}}_r+r\dot{\bm{\hat{e}}}_r\\ &=\dot{r} \bm{\hat{e}}_r+r\bm{\omega}\times\bm{\hat{e}}_r\\ &=\dot{r} \bm{\hat{e}}_r+r(\dot{\varphi}\bm{\hat{e}}_z+\dot{\theta}\bm{\hat{e}}_\varphi)\times\bm{\hat{e}}_r\\ &=\dot{r} \bm{\hat{e}}_r+r\dot{\theta}\bm{\hat{e}}_\theta+r\dot{\varphi}\sin\theta \bm{\hat{e}}_\varphi\\ \end{aligned}

加速度：

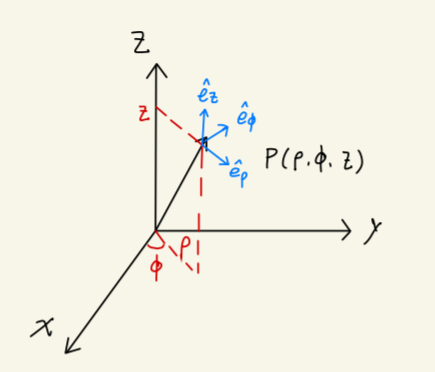
a=(r¨−rθ˙2−rφ˙2sin⁡2θ)e^r+(2r˙θ˙+rθ¨−rφ˙2sin⁡θcos⁡θ)e^θ+(2r˙φ˙sin⁡θ+rφ¨sin⁡θ)e^φ\begin{aligned} \bm{a}=&(\ddot{r}-r\dot{\theta}^2-r\dot{\varphi}^2\sin^2\theta)\bm{\hat{e}}_{r}\\ &+(2\dot{r}\dot{\theta}+r\ddot{\theta}-r\dot{\varphi}^2\sin\theta\cos\theta)\bm{\hat{e}}_{\theta}\\ &+(2\dot{r}\dot{\varphi}\sin\theta+r\ddot{\varphi}\sin\theta)\bm{\hat{e}}_{\varphi}\\ \end{aligned}

Fig1.5：柱坐标系

在柱坐标系中，我们用 (ρ,ϕ,z)(\rho,\phi,z) 分别表示径向距离、方位角、高度。

质点位置：

r=ρe^ρ+ze^z\bm{r}=\rho\bm{\hat{e}}_{\rho}+z\bm{\hat{e}}_z

角速度：

ω=ϕ˙e^ϕ\bm{\omega}=\dot{\phi}\bm{\hat{e}}_{\phi}

速度：

v=ρ˙e^ρ+ρϕ˙e^ϕ+z˙e^z\bm{v}=\dot{\rho}\bm{\hat{e}}_{\rho}+\rho\dot{\phi}\bm{\hat{e}}_{\phi}+\dot{z}\bm{\hat{e}}_z

加速度：

a=(ρ¨−ρϕ˙2)e^ρ+(2ρ˙ϕ˙+ρϕ¨)e^ϕ+z¨e^z\bm{a}=(\ddot{\rho}-\rho\dot{\phi}^2)\bm{\hat{e}}_{\rho}+(2\dot{\rho}\dot{\phi}+\rho\ddot{\phi})\bm{\hat{e}} _{\phi}+\ddot{z}\bm{\hat{e}}_z

参考系与坐标变换

参考系

在具体讲述之前，先思考一个问题：
坐标系与参考系的关系是怎样的？

以下谈谈我的看法：
在之前的讲解中，我们模糊了参考系与坐标系的概念。我的观点是：坐标是一个参考系的一个附加结构，一方面：虽然运动本身是坐标无关的，但这个结构对于分量描述质点的运动是必要的。另一方面，坐标变换将不同的参考系联系起来。另外在有些时候，参考系更多的只是充当一个观察者，例如对火车速度的观察，我们以地面为参考系，并没有指定以地上某个点为原点建立坐标系，而是指定了一类与地面相对静止的参考系。

wiki中的定义：参考系（又称参照系、参考坐标），在物理学中指用以测量并记录位置、定向以及其他物体属性的坐标系；或指与观测者的运动状态相关的观测参考系；又或同指两者[2]^{[2]}。

坐标变换

同一参考系不同坐标之间的变换

对于一般的坐标微元 (dx1,dx2,dx3)(dx_1,dx_2,dx_3) 到 (dx1′,dx2′,dx3′)(dx_1',dx_2',dx_3') 之间的变换。利用雅可比矩阵，有：

(dx1′dx2′dx3′)=(∂x1′∂x1∂x1′∂x2∂x1′∂x3∂x2′∂x1∂x2′∂x2∂x2′∂x3∂x3′∂x1∂x3′∂x2∂x3′∂x3)(dx1dx2dx3)\begin{aligned} \begin{pmatrix}dx_1' \\ \\ dx_2'\\ \\ dx_3'\end{pmatrix}=\begin{pmatrix}\frac{\partial x_1'}{\partial x_1} & \frac{\partial x_1'}{\partial x_2}& \frac{\partial x_1'}{\partial x_3}\\ \\ \frac{\partial x_2'}{\partial x_1} & \frac{\partial x_2'}{\partial x_2}& \frac{\partial x_2'}{\partial x_3} \\ \\\frac{\partial x_3'}{\partial x_1} & \frac{\partial x_3'}{\partial x_2}& \frac{\partial x_3'}{\partial x_3}\\\end{pmatrix}\begin{pmatrix}dx_1 \\ \\ dx_2\\ \\ dx_3\end{pmatrix} \end{aligned}

其中雅可比矩阵为：

J(x1,x2,x3)=(∂xi′∂xj)3×3J(x_1,x_2,x_3)=(\frac{\partial x'_i}{\partial x_j})_{3\times 3}

将以上变换简记为：

dx′=Jdx\bm{dx'}=\bm{J}\bm{dx}

在经典力学中，位置间隔在坐标变换中不变（相对论中对应时空间隔不变）：

d2s=∣dx∣2=dx12+dx22+dx32\begin{aligned} &d^2s=|\bm{dx}|^2=\sqrt{dx_1^2+dx_2^2+dx_3^2}\\ \end{aligned}

不难求得，变换后的间隔

ds′2=dx′Tdx′=dxTJTJdx=h12dx12+h22dx22+h32dx32=ds2\begin{aligned} ds'^2&=\bm{dx'}^T\bm{dx'}\\ &=\bm{dx}^TJ^TJ\bm{dx}\\ &=h_1^2dx_1^2+h_2^2dx_2^2+h_3^2dx_3^2\\ &=ds^2 \end{aligned}

其中 hih_i 为坐标变换中对应坐标的 lame系数

hi=∑j(∂xj′∂xi)2h_i = \sqrt{\sum_{j}(\frac{\partial x_j'}{\partial x_i})^2}

体积元：

dV=dx1dx2dx3=h1h2h3dx1′dx2′dx3′=Jdx1′dx2′dx3′\begin{aligned} dV&=dx_1dx_2dx_3\\ &=h_1h_2h_3dx'_1dx'_2dx'_3\\ &=Jdx'_1dx'_2dx'_3\\ \end{aligned}

对应变换后的基矢量为：

e^i′=∂x∂xi′/∣∂x∂xi′∣=1hi∂x∂xi′\begin{aligned} \bm{\hat{e}'_i}&=\frac{\partial \bm{x}}{\partial {x'_i}}/|\frac{\partial \bm{x}}{\partial {x'_i}}|\\ &=\frac{1}{h_i}\frac{\partial \bm{x}}{\partial {x'_i}}\\ \end{aligned}

若：

  • det⁡J=1\det{J}=1，保持定向。
  • det⁡J=−1\det{J}=-1，逆转定向。

保持定向指变换后基矢构成的手性与原基矢手性相同，逆转定向指两者相反。

要从坐标微元变换到坐标变换，只需要进行积分。

举例：
球坐标到直角坐标
坐标变换为 (r,θ,ϕ)→(x,y,z)(r,\theta,\phi)\rightarrow(x,y,z)：

{x=rsin⁡θcos⁡φy=rsin⁡θsin⁡φz=rcos⁡θ\left\{\begin{aligned} & x = r\sin\theta\cos\varphi\\ & y = r\sin\theta\sin\varphi\\ & z = r\cos\theta\\ \end{aligned}\right.

对应的雅可比矩阵：

J(r,θ,ϕ)=(sin⁡θcos⁡φrcos⁡θcos⁡φ−rsin⁡θsin⁡φsin⁡θsin⁡φrcos⁡θsin⁡φrsin⁡θcos⁡φcos⁡θ−rsin⁡θ0)J(r,\theta,\phi)=\begin{pmatrix}\sin\theta\cos\varphi & r\cos\theta\cos\varphi & -r\sin\theta\sin\varphi\\ \\ \sin\theta\sin\varphi & r\cos\theta\sin\varphi & r\sin\theta\cos\varphi\\ \\ \cos\theta & -r\sin\theta & 0\\ \end{pmatrix}

lame 系数：

hr=1, hθ=r,hφ=rsin⁡θh_{r}=1,\ h_{\theta}=r,h_{\varphi}=r\sin\theta

det⁡J=r2sin⁡θ>0\det{J}=r^2\sin\theta>0

该变换将保持定向。

变换后基矢：

e^r′=(sin⁡θcos⁡φ,sin⁡θsin⁡φ,cos⁡θ)e^θ′=(cos⁡θcos⁡φ,cos⁡θsin⁡φ,−sin⁡θ)e^φ′=(−sin⁡φ,cos⁡φ,0)\begin{aligned} \bm{\hat{e}'_r}&=(\sin\theta\cos\varphi, \sin\theta\sin\varphi,\cos\theta)\\ \bm{\hat{e}'_\theta}&=(\cos\theta\cos\varphi, \cos\theta\sin\varphi,-\sin\theta)\\ \bm{\hat{e}'_\varphi}&=(-\sin\varphi, \cos\varphi,0)\\ \end{aligned}

举例
旋转
以 xyxy 平面内旋转为例，有：

(x′y′z′)=(cos⁡θ−sin⁡θ0sin⁡θcos⁡θ0001)(xyz)\begin{pmatrix}x' \\ y' \\ z' \end{pmatrix}=\begin{pmatrix}\cos\theta & -\sin\theta & 0\\ \sin\theta & \cos\theta & 0\\ 0 & 0 & 1\\ \end{pmatrix}\begin{pmatrix}x \\ y \\ z \end{pmatrix}

可以记做：

r′=M(θ)r\bm{r}'=\bm{M}(\theta)\bm{r}

推广到绕轴 n^\hat{\bm{n}} 旋转角度 θ\theta，有：

r′=M(n^,θ)r\bm{r}'=\bm{M}(\hat{\bm{n}},\theta)\bm{r}

不难得到：

det⁡M(n^,θ)=1\det \bm{M}(\hat{\bm{n}},\theta)=1

这意味着，旋转变换保间隔与定向。

进一步讨论，考虑在 dtdt 时间内，转动 dθd\theta，此时 M(e^z,dθ)\bm{M}(\bm{\hat{e}}_z,d\theta) 写做：

M(e^z,dθ)=(1−dθ0dθ10001)=1+Mzdθ\begin{aligned} \bm{M}(\bm{\hat{e}}_z,d\theta) &=\begin{pmatrix}1 & -d\theta & 0\\ d\theta & 1 & 0\\ 0 & 0 & 1\\ \end{pmatrix}\\ &=1+M_z d\theta\\ \end{aligned}

可得到：

Mx=(001000−100),My=(0−10100000),Mz=(00000−1010)M_x=\begin{pmatrix}0 & 0 & 1 \\ 0 & 0 & 0\\ -1 & 0 & 0\\\end{pmatrix},M_y=\begin{pmatrix}0 & -1 & 0 \\ 1 & 0 & 0\\ 0 & 0 & 0\\\end{pmatrix},M_z=\begin{pmatrix}0 & 0 & 0 \\ 0 & 0 & -1\\ 0 & 1 & 0\\\end{pmatrix}

对于任意一个无限小转动 dθ=ωdtd\bm{\theta}=\bm{\omega}dt，有：

r′=M(ωdt)r=M(e^z,ωzdt)M(e^z,ωzdt)M(e^z,ωzdt)r=(1+Mxωxdt)(1+Myωydt)(1+Mzωzdt)r≈(1+∑iMiωidt)r\begin{aligned} \bm{r}'&=\bm{M}(\bm{\omega}dt)\bm{r}\\ &=\bm{M}(\bm{\hat{e}}_z,\omega_zdt) \bm{M}(\bm{\hat{e}}_z,\omega_zdt) \bm{M}(\bm{\hat{e}}_z,\omega_zdt) \bm{r}\\ &=(1+M_x \omega_x dt)(1+M_y \omega_y dt)(1+M_z \omega_z dt)\bm{r}\\ &\approx (1+\sum_{i}M_i \omega_i dt)\bm{r}\\ \end{aligned}

可得

dr′dt=dMdtr=∑iMiωir\frac{d\bm{r'}}{dt}=\frac{d\bm{M}}{dt}\bm{r}=\sum_{i}M_i\omega_i\bm{r}

且有：

dMdt=∑iMiωi=(0−ωyωzωy0−ωz−ωxωz0)\frac{d\bm{M}}{dt}=\sum_{i}M_i\omega_i=\begin{pmatrix}0 & -\omega_y & \omega_z \\ \omega_y & 0 & -\omega_z\\ -\omega_x & \omega_z & 0\\\end{pmatrix}

注意到：

dr′dt=ω×r\frac{d\bm{r'}}{dt}=\bm{\omega}\times\bm{r}

这与我们前一节中直接给出的结论是一致的。

举例
反射
以 xyxy 平面反射为例：

(x′y′z′)=(10001000−1)(xyz)\begin{pmatrix}x' \\ y' \\ z' \end{pmatrix}=\begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & -1\\ \end{pmatrix}\begin{pmatrix}x \\ y \\ z \end{pmatrix}

det⁡M=−1\det{\bm{M}} = -1

这意味着，反射变换保间隔且逆转定向。

不同参考系之间的变换

设有参考系 SS，S′S'，其中参考系 SS 是静止的，S′S' 原点在 SS 中的位矢为 Δr\Delta \bm{r}。设 SS 坐标 (x1,x2,x3)(x_1,x_2,x_3) 到 S′S' 坐标 (x1′,x2′,x3′)(x_1',x_2',x_3') 的坐标变换为 MM。

现在有一质点 PP，在 SS 中的坐标为 rS\bm{r}_ S，在 S′S' 中的坐标为 r′S′\bm{r'}_{S'}

于是，有：

r′S′=M(rS−ΔrS)\bm{r'}_{S'}=\bm{M}(\bm{r}_S-\Delta \bm{r}_S)

或者为：

rS=M−1rS′′+ΔrS\bm{r}_S = \bm{M}^{-1}\bm{r}'_{S'}+\Delta\bm{r}_S

举例：
伽利略变换

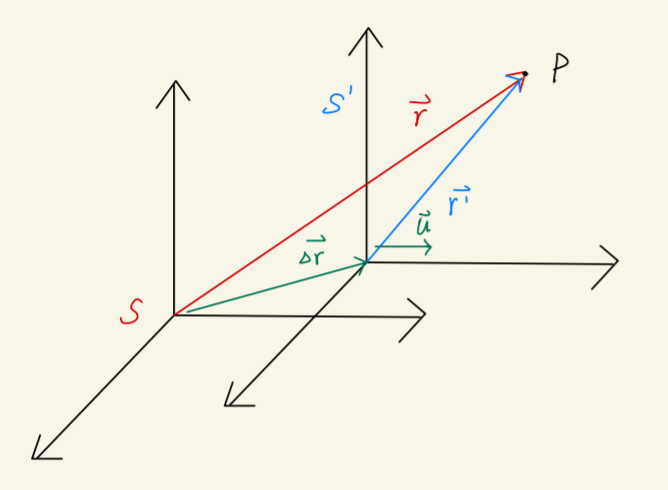
Fig1.6：伽利略变换

参考系 S,S′S,S' 相对速度恒定。即：

ΔrS=rS0+uSt\bm{\Delta r}_S=r^{0}_{S}+\bm{u}_St

且要求：

dMdt=0\frac{d\bm{M}}{dt}=0

有：

{r′S′=M(rS−rS0−uSt)v′S′=M(vS−uS)a′S′=MaS\left\{ \begin{aligned} & \bm{r'}_{S'}=\bm{M}(\bm{r}_ {S}-\bm{r}^{0}_{S}-\bm{u}_{S}t)\\ & \bm{v'}_{S'}=\bm{M}(\bm{v}_S- \bm{u}_{S})\\ & \bm{a'}_{S'}=\bm{M}\bm{a}_S\\ \end{aligned} \right.

若两参考系的取向、选取的坐标均相同，即 M=I\bm{M}=\bm{I}，此时得到，我们熟悉的伽利略变换的形式：

{r′=r−r0−utv′=v−ua′=a\left\{ \begin{aligned} & \bm{r'}=\bm{r}-\bm{r}_{0}-\bm{u}t\\ & \bm{v'}=\bm{v}- \bm{u}\\ & \bm{a'}=\bm{a}\\ \end{aligned} \right.

举例
匀速转动参考系
参考系 S,S′S,S' 初始重合，且原点始终重合，S′S' 相对 SS 以 ω\omega 匀速转动：
需要注意，在之前的讨论中，我们采用的是主动将位矢进行旋转的“主动观点”。若对应到转动参考系导致位矢变化的“被动观点”，等价为使用 −ω-\bm{\omega} 转动位矢的主动观点。
因此：

M=M(−ωt),ΔrS=0\bm{M}=\bm{M}(\bm{-\omega} t),\Delta \bm{r}_S =0

有：

rS=M−1rS′\bm{r}_{S}=\bm{M}^{-1}\bm{r}_{S'}

vS=drSdt=dM−1dtrS′+M−1drS′dt=ω×rS′+M−1vS′\begin{aligned} \bm{v}_{S}&=\frac{d\bm{r}_{S}}{dt}\\ &=\frac{d \bm{M}^{-1}}{dt}\bm{r}_{S'}+\bm{M}^{-1}\frac{d\bm{r}_{S'}}{dt}\\ &=\bm{\omega}\times\bm{r}_{S'}+\bm{M}^{-1}\bm{v}_{S'} \end{aligned}

aS=dvSdt=ddt(ω×rS′+M−1vS′)=M−1aS′+ω×(ω×rS′)+2ω×vS′\begin{aligned} \bm{a}_S&=\frac{d\bm{v}_S}{dt}\\ &=\frac{d}{dt}(\bm{\omega}\times\bm{r}_{S'}+\bm{M}^{-1}\bm{v}_{S'})\\ &=\bm{M}^{-1}\bm{a}_{S'}+\bm{\omega}\times(\bm{\omega}\times\bm{r}_{S'})+2\bm{\omega}\times\bm{v}_{S'} \end{aligned}

与使用 SS 的坐标直接表示 aS′\bm{a}_{S'} 的加速度 M−1aS′\bm{M}^{-1}\bm{a}_{S'} 相比，aS\bm{a}_S 多出了两项。这是由参考系 S′S' 的转动所导致的。我们将这部分的总和称作 牵连加速度。具体分析：

  • ω×(ω×rS′)\bm{\omega}\times(\bm{\omega}\times\bm{r}_{S'})：由转动导致，在质点不在转轴的情况下不为零。这个加速度被称为 向心加速度。
  • 2ω×vS′2\bm{\omega}\times\bm{v}_{S'}：由参考系的转动和质点的相对运动导致，只有在角速度方向与质点运动方向平行时才为零。这一项被称为 科里奥利加速度。

举例
一般相对运动

Fig1.7：一般相对运动

参考系 S,S′S,S' ，S′S' 相对 SS 以 ω(t)\omega(t) 转动，S′S' 相对 ’SS 原点相对位矢为 ΔrS\Delta \bm{r}_S：
同理可得：

rS=ΔrS+M−1r′S′\bm{r}_{S}=\Delta \bm{r}_S+\bm{M}^{-1}\bm{r'}_{S'}

vS=drSdt=ΔvS+ω×r′S′+M−1v′S′\begin{aligned} \bm{v}_{S}&=\frac{d\bm{r}_{S}}{dt}\\ &=\Delta\bm{v}_S+\bm{\omega}\times\bm{r'}_{S'}+\bm{M}^{-1}\bm{v'}_{S'}\\ \end{aligned}

aS=dvSdt=ddt(ΔvS+ω×r′S′+M−1v′S′)=M−1aS′′+2ω×v′S′+β×r′S′+ω×(ω×r′S′)+ΔaS\begin{aligned} \bm{a}_S&=\frac{d\bm{v}_S}{dt}\\ &=\frac{d}{dt}(\Delta\bm{v}_S+\bm{\omega}\times\bm{r'}_{S'}+\bm{M}^{-1}\bm{v'}_{S'})\\ &=\bm{M}^{-1}\bm{a}'_{S'}+2\bm{\omega}\times\bm{v'}_{S'}+\bm{\beta}\times\bm{r'}_{S'}+\bm{\omega}\times(\bm{\omega}\times\bm{r'}_{S'})+\Delta\bm{a}_S\\ \end{aligned}

观察加速度的表达式，牵连加速度共有四项。其中两项是我们之前提到的向心加速度与科里奥利加速度。剩下两项：

  • β×r′S′\bm{\beta}\times \bm{r'}_{S'}：参考系的加速转动产生。
  • ΔaS\Delta \bm{a}_S：参考系的平动加速度。

若我们选取 M∣t=0=I\bm{M}|_{t=0} = \bm{I}，即所讨论的 t=0t=0 时刻，两个参考系选择同种坐标，且取向相同。那么：速度与加速度可以表示为：

vS=ΔvS+ω×r′S′+v′S′aS=aS′′+2ω×v′S′+β×r′S′+ω×(ω×r′S′)+ΔaS\begin{aligned} \bm{v}_{S}&=\Delta\bm{v}_S+\bm{\omega}\times\bm{r'}_{S'}+\bm{v'}_{S'}\\ \bm{a}_S&=\bm{a}'_{S'}+2\bm{\omega}\times\bm{v'}_{S'}+\bm{\beta}\times\bm{r'}_{S'}+\bm{\omega}\times(\bm{\omega}\times\bm{r'}_{S'})+\Delta\bm{a}_S\\ \end{aligned}

总结

  • 在本篇笔记中，如何描述 质点的运动 是我们的核心问题。运动是相对的，为了描述运动，我们必须要引入一个 参考系。给定参考系后，我们用 位矢、速度、加速度 描述质点的平动。接下来，我们引入不同的坐标对运动进行分量描述。在直角坐标系中，这点是很好办的。然而在球坐标与柱坐标中，由于引入了角位置。必须考虑如何描述质点的 角运动。

  • 参考系的坐标变换将各种参考系联系起来。我们使用矩阵方法分析了在不同的坐标变换下，质点的运动量将如何变换。讨论了 平动参考系 与 平动参考系、平动参考系 与 转动参考系 之间的变换。其中的结果将在下一篇中有所应用。

参考资料

  1. J.L. Meriam, L.G. Kraige, “Engineering Mechanics: Dynamics,” 第三版，ISBN 0471592730。
  2. 维基百科编者. 参考系[G/OL]. 维基百科, 202020201231. https://zh.wikipedia.org/w/index.php?title=参考系&oldid=63511353.
  3. 梁昆淼，《力学》，下册
  4. 朗道，《力学》