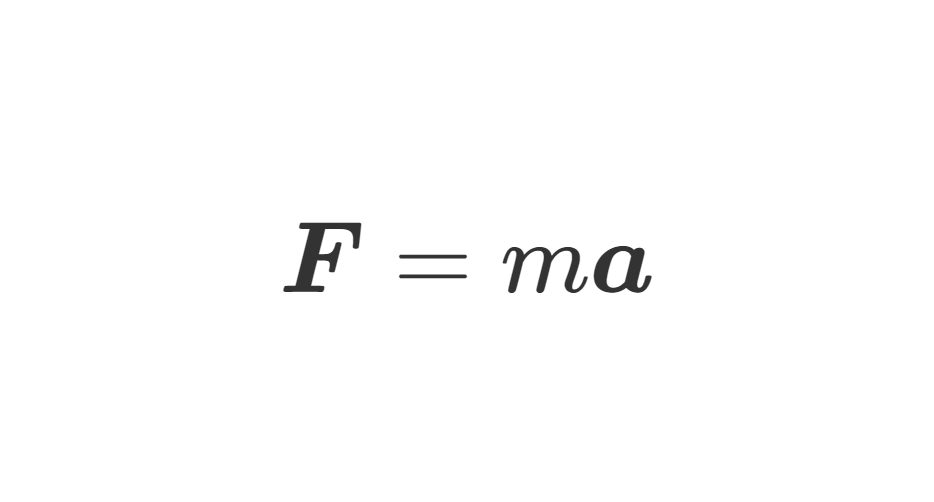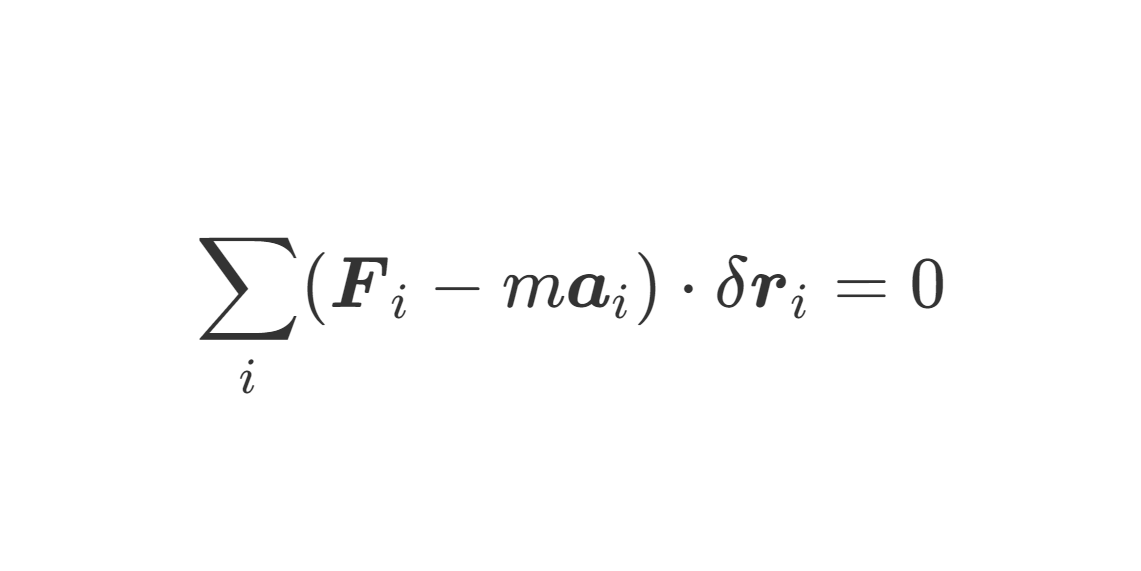理论力学笔记（四）：拉格朗日力学

拉格朗日力学

拉格朗日方程

现在从 达朗贝尔原理 出发推导拉格朗日方程 $^{[1]}$ ：

$\sum_{i}(\bm{F}_i - m\bm{a}_i)\cdot\delta\bm{r}_i = 0$

对于一个自由度为 $s$ 的系统，可以选取一组相互独立的广义坐标 $\{q_1,q_2\cdots,q_s\}$ 。将达朗贝尔原理中的坐标用广义坐标替代：
可得虚位移为：

$\delta \bm{r}_i = \sum_{j = 1}^{s} \frac{\partial \bm{r}_i}{\partial q_{j}} \delta q_{j}$

速度为：

$\begin{aligned} \bm{v}_i &= \frac{d\bm{r}_i}{dt}\\ &= \frac{\partial \bm{r}_i}{\partial t} + \sum_{j=1}^{s}\frac{\partial \bm{r}_i}{\partial q_{j}} \dot{q}_j \end{aligned}$

有：

$\frac{\partial \bm{v}_i}{\partial \dot{q}_j} = \frac{\partial \bm{r}_i}{\partial q_j}$

考虑达朗贝尔原理中的加速度项：

$\begin{aligned} \sum_{i} m\bm{a}_i \cdot\delta\bm{r}_i &=\sum_{ij} m \bm{a}_i\cdot\frac{\partial \bm{r}_i}{\partial q_{j}} \delta q_{j} \\ &=\sum_{ij} m [\frac{d}{dt}(\bm{v}_i\cdot\frac{\partial \bm{r}_i}{\partial q_j})-\bm{v}_i\cdot\frac{d}{dt}\frac{\partial \bm{r}_i}{\partial q_j}] \delta q_{j}\\ &=\sum_{ij} m [\frac{d}{dt}(\bm{v}_i\cdot\frac{\partial \bm{v}_i}{\partial \dot{q}_j})-\bm{v}_i\cdot\frac{\partial \bm{v}_i}{\partial q_j}] \delta q_{j}\\ &=\sum_{j}[\frac{d}{dt}(\frac{\partial T}{\partial \dot{q}_j})-\frac{\partial T}{\partial q_j}]\delta q_{j} \end{aligned}$

其中 $T = \frac{1}{2}\sum_i m\bm{v}_i\cdot\bm{v}_i$ 为体系的动能。

达朗贝尔原理中的含作用力项成为：

$\begin{aligned} \sum_{i}\bm{F}_i\cdot\delta\bm{r}_i &= \sum_{ij}\bm{F}_i\cdot\frac{\partial \bm{r}_i}{\partial q_{j}} \delta q_{j} \\ & = \sum_{j} \mathcal{F}_j\delta q_j \end{aligned}$

其中 $\mathcal{F}$ 为 广义力。

$\mathcal{F}_j = \sum_{i}\bm{F}_i\cdot\frac{\partial \bm{r}_i}{\partial q_{j}}$

由此，达朗贝尔原理可以利用广义坐标重新写做：

$\sum_{j}(\mathcal{F}_j-\frac{d}{dt}(\frac{\partial T}{\partial \dot{q}_j})+\frac{\partial T}{\partial q_j})\delta q_j = 0$

由虚位移 $\delta q_j$ 选取的任意性，得到：

$\mathcal{F}_j-\frac{d}{dt}(\frac{\partial T}{\partial \dot{q}_j})+\frac{\partial T}{\partial q_j} = 0$

我们称 $\frac{\partial T}{\partial \dot{q}}$ 为 广义动量， $\frac{\partial T}{\partial q}$ 为 拉格朗日力。
对于 单演系统 $^{[2]}$ ，有：

$\mathcal{F}_i = -\frac{\partial\mathcal{V}}{\partial q_i} + \frac{d}{dt}(\frac{\partial\mathcal{V}}{\partial \dot{q}_i})$

其中 $\mathcal{V}$ 为广义势能。

若 $F_i = -\frac{\partial V}{\partial q_i}$ ，该系统为保守系统。

由此得到 拉格朗日方程

$\frac{d}{dt}(\frac{\partial L}{\partial \dot{q}})-\frac{\partial L}{\partial q} = 0$

其中 $L \equiv T -V$ 为拉格朗日函数。

有很多初学者可能不懂得引入拉格朗日方程的意义。所以现在有必要回顾以下我们之前讲过的东西：从牛顿运动定律、达朗贝尔原理再到拉格朗日方程，我们花了很多功夫进行推导到底做了一件什么事情？
实际上，我们在进行一个 范式转变：

牛顿运动定律：力决定了每个质点的运动。

达朗贝尔原理：不必考虑约束。

拉格朗日方程：系统的能量决定了系统的运动。

进行这个范式转变具有很重要的意义，因为相比于力来说，能量是一个更为普适的概念，就更容易进行推广。虽然拉格朗日力学的物理图像没有牛顿力学那么容易想象，但其相比牛顿力学具有很多优越的地方：拉格朗日力学中系统的运动完全由能量的性质决定；不用考虑约束；导出的标量方程组比牛顿运动定律的矢量方程组更简单。

哈密顿原理

上一节的推导从达朗贝尔原理出发，也就是基于牛顿运动方程的。接下来，我们不以牛顿运动方程为基础推导拉格朗日方程。

注意：现在最好忘记牛顿力学！

根据 哈密顿原理（或称 最小作用量原理 ），每一个力学体系可以用一个函数来描述 $^{[3]}$ ：

$L(q_1,q_2,\cdot,q_s,\dot{q}_1,\dot{q}_2,\cdot,\dot{q}_s,t)$

简写为 $L(q,\dot{q},t)$ 。这个函数完全确定系统的位形（这里位形包括坐标空间与动量空间）。考虑这个函数随时间的积分：

$S = \int_{t_1}^{t_2} L(q,\dot{q},t)dt$

定义为 作用量，每一种可能的系统随时间的演化情况都会得到一个作用量。哈密顿原理要求：真实运动应当使作用量取极小值。即：

$\delta S = 0$

首先指出，哈密顿原理采用的变分为 等时变分，这意味着：

$d$ 和 $\delta$ 操作可以交换顺序。因为 $d$ 是随时间演化的微分， $\delta$ 是在固定时刻考虑位形的变化。

$\delta t = 0$ ，这是自然的。

另外考虑到变分的边界条件，即在初态末态的位形是固定的，此刻的变分自然为零。

我们先根据哈密顿原理推导拉格朗日方程，再回过头来具体阐述物理意义。

$\begin{aligned} \delta S&=\delta \int_{t_1}^{t_2} L(q,\dot{q},t)dt\\ &=\int_{t_1}^{t_2} \delta L(q,\dot{q},t)dt\\ &=\int_{t_1}^{t_2} (\frac{\partial L}{\partial q}\delta q+\frac{\partial L}{\partial \dot{q}}\delta \dot{q})dt\\ &=\int_{t_1}^{t_2} \frac{\partial L}{\partial q}\delta qdt+\frac{\partial L}{\partial \dot{q}}\delta dq\\ &=\int_{t_1}^{t_2} \frac{\partial L}{\partial q}\delta qdt+\frac{\partial L}{\partial \dot{q}} d\delta q\\ &=\frac{\partial L}{\partial \dot{q}} \delta q|_{t_1}^{t_2}+ \int_{t_1}^{t_2} (\frac{\partial L}{\partial q}-\frac{d}{dt}(\frac{\partial L}{\partial \dot{q}}))\delta qdt\\ &=\int_{t_1}^{t_2} (\frac{\partial L}{\partial q}-\frac{d}{dt}(\frac{\partial L}{\partial \dot{q}}))\delta qdt\\ \end{aligned}$

考虑到 $\delta q$ 选取的任意性，根据哈密顿原理立即得到：

$\frac{\partial L}{\partial q}-\frac{d}{dt}(\frac{\partial L}{\partial \dot{q}}) = 0$

该式在形式上与拉格朗日方程是一致的。我们不妨定义这个函数为体系的 拉格朗日函数 或 拉格朗日量，若体系的拉格朗日函数已知，那么就能够推导出体系的运动方程。

拉格朗日函数

现在考虑拉格朗日函数的性质。

一个体系的拉格朗日函数不必是唯一的，只要其导出的运动方程（拉格朗日方程）一致，那么这两个拉格朗日函数就是等价的。

例如： $L(q,\dot{q},t)$ 与 $L(q,\dot{q},t)+c$ （ $c$ 为常数）是等价的。
更一般的，考虑为 $L$ 加上一个如下一项：

$\frac{d}{dt}f(q,\dot{q},t)$

容易得到，加上如上项对应的作用量会增加一个常量，不改变作用量的变分，也不会改变运动方程。

拉格朗日函数具有可加性。

具体来说，考虑两个系统 $A,B$ ，拉格朗日函数分别为 $L_A,L_B$ ，假设这两个系统间的相互作用很弱，那么有对于 $A,B$ 分别有哈密顿原理：

$\delta_A S = 0;\quad \delta_B S = 0$

这要求作用量必定是可加的，即：

$S = S_A + S_B$

对应的拉格朗日也必定具有可加性：

$L = L_A + L_B$

拉格朗日函数乘以一个常数，运动方程不改变。

实际上，这相当于选取了不同的单位制，我们在 力学相似性 中还会介绍。

现在我们来考虑拉格朗日函数的具体形式。
首先考虑 自由单粒子 的拉格朗日函数。

单粒子的拉格朗日函数可以写做 $L(\bm{r},\bm{v},t)$ 。

空间与时间的均匀性，拉格朗日函数应当与 $\bm{r},t$ 无关。写做 $L(\bm{v})$
空间的各向同性意味拉格朗日函数与粒子运动的方向无关。由此： $L = L(v^2)$
考虑一个伽利略变换，使得 $\bm{v}\rightarrow \bm{v}+\bm{\varepsilon}$ ，其中 $\varepsilon$ 为一个小量。由此：

$L((\bm{v}+\bm{\varepsilon})^2) = L(v^2) + \frac{\partial L}{\partial v^2} 2\bm{v}\cdot\bm{\varepsilon}$

在伽利略变换下，运动方程不应当发生变化。由此，拉格朗日函数至多相差一个全微商。由此可得 $L \propto v^2$ ，我们写做：

$L = \frac{1}{2}mv^2$

我们定义 $m$ 为质量。

对于自由质点可以写出运动方程：

$\dot{\bm{v}} = \frac{1}{m}\frac{d}{dt}\frac{\partial L}{\partial \bm{v}} = \frac{1}{m}\frac{\partial L}{\partial \bm{r}} = 0$

即速度为常数，这对应 惯性定律。

注意到，单粒子的拉格朗日量只有速度项，且这一部分为粒子的运动产生，我们定义其为单粒子的动能 $T$ ：

$T = \frac{1}{2}mv^2$

当粒子在场中运动时，拉格朗日量需要引入一个可能依赖坐标的势能项 $V$ ，于是得到：

$L = T - V$

对于质点组来说，拉格朗日量为：

$L = \sum_{i}\frac{1}{2}m_iv_i^2 - U(q_1,q_2,\cdots)$

对应的拉格朗日方程为：

$m_i\bm{a}_i = -\frac{\partial U}{\partial \bm{r}_i} = \bm{F}$

这就是 牛顿第二定律。这也说明了，为什么拉格朗日量中的势能项为负号。

例：双摆

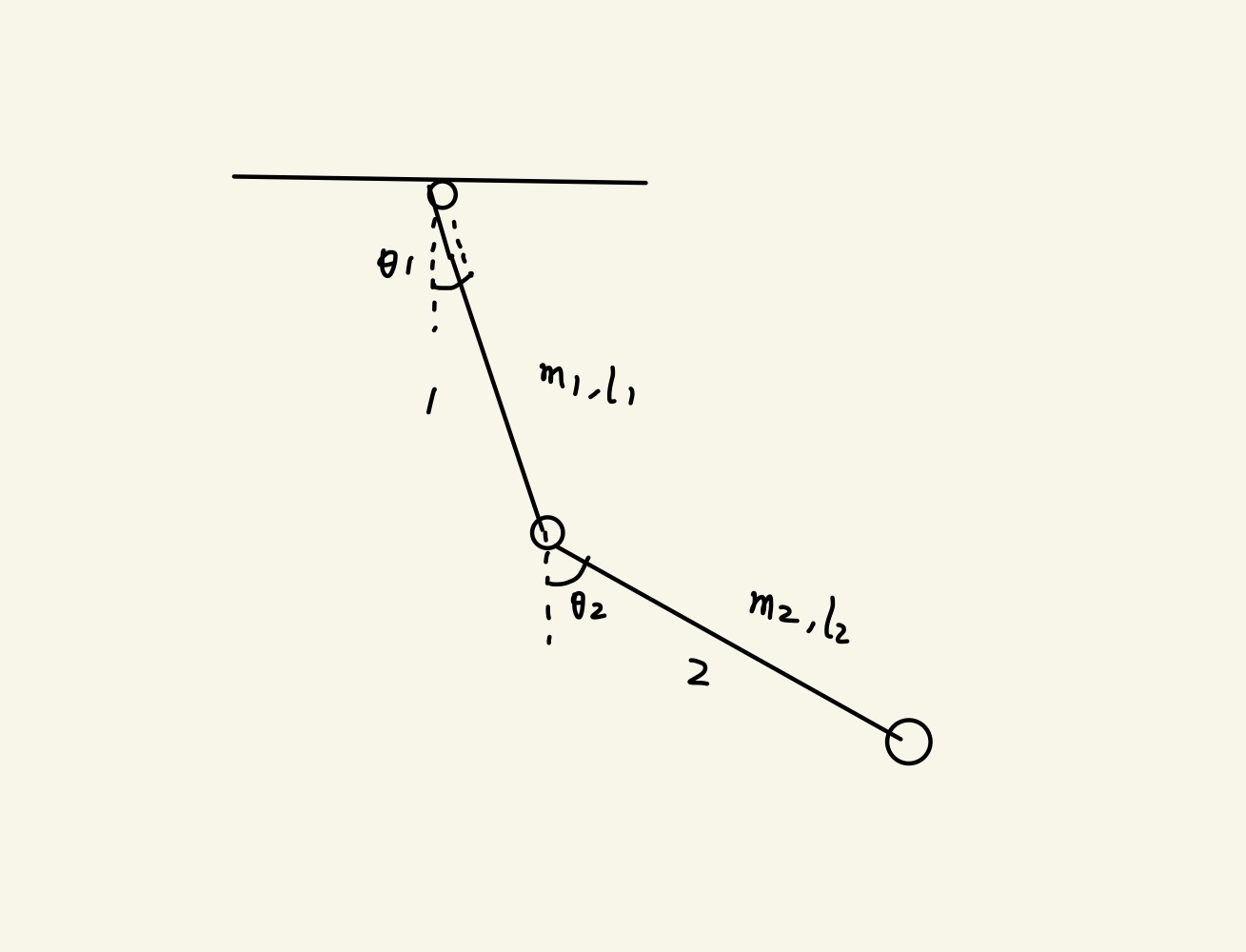
选取广义坐标为 $\theta_1$ ， $\theta_2$ ，写出球1、2的位置：

$\left\{ \begin{aligned} &x_1 = l_1\sin\theta_1\\ &y_1 = -l_1\cos\theta_1\\ &x_2 = l_1\sin\theta_1+l_2\sin\theta_2\\ &y_2 = -l_1\cos\theta_1-l_2\cos\theta_2\\ \end{aligned} \right.$

可得：

$\left\{ \begin{aligned} &\dot{x}_1 = l_1\cos\theta_1 \dot{\theta}_1\\ &\dot{y}_1 = l_1\sin\theta_1\dot{\theta}_1\\ &\dot{x}_2 = l_1\cos\theta_1\dot{\theta}_1+l_2\cos\theta_2\dot{\theta}_2\\ &\dot{y}_2 = l_1\sin\theta_1\dot{\theta}_1+l_2\sin\theta_2\dot{\theta}_2\\ \end{aligned} \right.$

动能写做：

$\begin{aligned} T &= \frac{1}{2}m_1(\dot{x}_1^2+\dot{y}_1^2)+\frac{1}{2}m_2(\dot{x}_2^2+\dot{y}_2^2)\\ &=\frac{1}{2}(m_1+m_2)l_1^2\dot{\theta}_1^2 + \frac{1}{2}m_2l_2^2\dot{\theta}_2^2+m_2l_1l_2\dot{\theta}_1\dot{\theta}_2\cos(\theta_1-\theta_2)\\ \end{aligned}$

势能为：

$\begin{aligned} U &= m_1gy_1+m_2gy_2\\ &= -(m_1l_1+m_2l_2)g\cos\theta_1 - m_2l_2 g\cos\theta_2\\ \end{aligned}$

拉格朗日量为：

$\begin{aligned} L & = T - U\\ & = \frac{1}{2}(m_1+m_2)l_1^2\dot{\theta}_1^2 + \frac{1}{2}m_2l_2^2\dot{\theta}_2^2+m_2l_1l_2\dot{\theta}_1\dot{\theta}_2\cos(\theta_1-\theta_2)+\\ &\quad (m_1l_1+m_2l_2)g\cos\theta_1+m_2l_2 g\cos\theta_2\\ \end{aligned}$

对应的拉格朗日方程为：

$\left\{ \begin{aligned} &\frac{d}{dt}((m_1+m_2)l_1^2\dot{\theta}_1+m_2l_1l_2\dot{\theta}_2\cos(\theta_1-\theta_2)) = -m_2l_1l_2\dot{\theta}_1\dot{\theta}_2\sin(\theta_1-\theta_2)-(m_1l_1+m_2l_2)g\sin\theta_1\\ &\frac{d}{dt}(m_2l_2^2\dot{\theta}_2+m_2l_1l_2\dot{\theta}_1\cos(\theta_1-\theta_2)) = m_2l_1l_2\dot{\theta}_1\dot{\theta}_2\sin(\theta_1-\theta_2)- m_2l_2 g\sin\theta_2\\ \end{aligned} \right.$

对称性与守恒律

在物理学中，对称性是一个十分重要的概念，也是一个非常漂亮的思想。在引入拉格朗日函数之后，我们可以做一些简单讨论。

在推导单质点的拉格朗日函数时，我们已经运用了对称性的思想。

对称性和操作联系起来。对称性就反映在体系在某个操作下的不变性。对于拉格朗日量 $L(q,\dot{q},t)$ ，考虑如下无穷小变换：

$q'= q+\epsilon(q,t),\quad t'= t +\eta$

有 $\epsilon,\eta\rightarrow 0$ ，这里认为 $\eta$ 是一个不依赖 $q,t$ 的量。
对应的速度变换为：

$\dot{q}'= \dot{q}+\dot{\epsilon}$

首先我们计算拉格朗日函数对时间的全微分：

$\begin{aligned} \frac{dL}{dt} &= \frac{\partial L}{\partial t} + \frac{\partial L}{\partial q} \dot{q} + \frac{\partial L}{\partial\dot{q}} \ddot{q} \\ &=\frac{\partial L}{\partial t} + (\frac{d}{dt}\frac{\partial L}{\partial \dot{q}}) \dot{q} + \frac{\partial L}{\partial\dot{q}} \ddot{q} \\ & = \frac{\partial L}{\partial t} + \frac{d}{dt}(\frac{\partial L}{\partial \dot{q}}\dot{q})\\ \end{aligned}$

由此：

$\frac{\partial L}{\partial t} = \frac{d}{dt}(L-\frac{\partial L}{\partial \dot{q}}\dot{q})$

我们将 $L-\frac{\partial L}{\partial \dot{q}}\dot{q}$ 记做 $H$ ，称为体系的 哈密顿量，这将在理论力学后面几篇详细介绍。那么得到：

$\frac{\partial L}{\partial t} = -\frac{dH}{dt}$

我们于是得到了变换后的拉格朗日量：

$\begin{aligned} L'(q',\dot{q}',t') &= L(q,\dot{q},t) + \frac{\partial L}{\partial q}\epsilon + \frac{\partial L}{\partial \dot{q}} \dot{\epsilon}+\frac{\partial L}{\partial t}\eta\\ &=L(q,\dot{q},t) + (\frac{d}{dt}\frac{\partial L}{\partial \dot{q}})\epsilon + \frac{\partial L}{\partial \dot{q}} \dot{\epsilon}+ \eta \frac{dH }{dt}\\ &=L(q,\dot{q},t) + \frac{d}{dt}(\frac{\partial L}{\partial \dot{q}}\epsilon+\eta H) \end{aligned}$

因为该变换是对称操作，体系的运动方程不应该变化。体现在变换前后的拉格朗日函数只能相差一个全微分项：

$L'(q',\dot{q}',t) = L(q,\dot{q},t) +\frac{dG}{dt}$

综合得到：

$\frac{d}{dt}(\frac{\partial L}{\partial \dot{q}}\epsilon+\eta H-G) = 0;\quad \frac{\partial L}{\partial \dot{q}}\epsilon+\eta H-G=\mathrm{const}$

我们得到了 Noether定理：连续对称性和守恒定律的一一对应。

函数 $G$ 似乎使得 Nother 定理所给出的守恒量带有很大程度上的“不确定性”。但需要说明，这个 $G$ 并不是能够随便选取的。 $G$ 函数应当取决于你所选取的变换操作。并且大多数时候，若你选取的操作是一个对称操作，那么 $G$ 会等于零。举例说明，对于以下拉格朗日量：

$L = \frac{1}{2}mv^2 - U(r)$

我们发现若绕过原点的轴进行一个旋转操作，上述拉格朗日量显然不会发生任何变化。
再举例：

$L = \frac{1}{2}mv^2$

考虑进行一个伽利略变换： $\bm{v}\rightarrow \bm{v+u}$
可得：

$\begin{aligned} L' &= \frac{1}{2}m(\bm{v}+\bm{u})^2\\ &= \frac{1}{2}mv^2 + m\bm{v}\cdot\bm{u} + \frac{1}{2}mu^2\\ &\sim \frac{1}{2}mv^2 + \frac{d}{dt}(m\bm{v}\cdot \Delta \bm{r}) \end{aligned}$

上述 $\Delta r$ 为变换前后参考系的相对位矢。（我们不关心多出来的常量）。可得：$G = m\bm{v}\cdot \Delta \bm{r} $。