原子核物理笔记（九）：原子核反应

核反应

核反应一般可以表示为：

$A + a \rightarrow B + b$

其中 $A$ 和 $a$ 分别表示靶核和出射粒子， $B$ 和 $b$ 表示剩余核和出射粒子。以上核反应简写为：

$A(a,b)B$

反应能

核反应中放出的能量，称为 反应能。用 $Q$ 表示。反应能就是反应前后的动能之差：那么：

$Q > 0$ 对应 放能反应
$Q < 0$ 对应 吸能反应

考虑反应能之后，核反应的表示式为：

$A + a \rightarrow B + b + Q$

根据反应能的定义得到：

$\begin{aligned} Q &= E_{Bk} + E_{bk} - E_{Ak} - E_{ak}\\ &= \Delta m c^2\\ &= (m_A+m_a-m_B- m_b)c^2\\ &\approx (M_A+M_a-M_B- M_b)c^2\\ \end{aligned}\tag{1}$

其中 $m,M$ 分别代表原子核、原子质量。
最后一个等式实际忽略了反应前后电子在原子中结合能的变化。

现在考虑通过实验测量反应中相关粒子的动能来求 $Q$ 值。

考虑在实验中，靶核往往是固定的。那么 $(1)$ 式成为：

$Q = E_{Bk} + E_{bk} - E_{ak} \tag{2}$

在实验中，剩余核的动能 $E_{Bk}$ 一般比较小，实验上很难测定。但是我们可以利用动量守恒定律消去 $E_{Bk}$ 。

动量守恒给出：

$\bm{p}_a = \bm{p}_B + \bm{p}_b$

可以得到：

$p_B^2 = p_a^2 + p_b^2 -2p_ap_b\cos\theta \tag{3}$

考虑 $p^2 = 2mE$ （不考虑相对论效应）。如此得到：

$m_BE_{kB} = m_aE_{ka} + m_bE_{kb} - 2(m_am_b E_{ka}E_{kb})^{1/2}\cos\theta$

代入 $(2)$ 式子，得到：

$Q = (\frac{m_a}{m_B}-1)E_{ka} + (\frac{m_b}{m_B}-1)E_{kb} - \frac{2(m_am_bE_{ka}E_{kb})^{1/2}\cos\theta}{m_B} \tag{4}$

将其中的质量之比换位质量数之比，进一步将 $(4)$ 写为：

$Q = (\frac{A_a}{A_B}-1)E_{ka} + (\frac{A_b}{A_B}-1)E_{kb} - \frac{2(A_aA_bE_{ka}E_{kb})^{1/2}\cos\theta}{A_B} \tag{5}$

如此，只要测量 $\theta$ 角方向上出射粒子的动能 $E_{kb}$ ，就可以求得 $Q$ 值。在 $\theta = 90\degree$ 时进行的计算更为容易。

另外的，若已知 $Q$ ， $(5)$ 式隐性的决定了 $E_{kb}$ 随 $\theta$ 的变化关系，我们显式表示为：

$E_b = \{ \frac{(A_aA_bE_a)^{1/2}}{A_B+A_b}\cos\theta \pm [(\frac{A_B-A_a}{A_B+A_b} + \frac{A_aA_b}{(A_B+A_a)^2}\cos^2\theta)E_a + \frac{A_B}{A_B+A_a}Q]^{1/2} \}^2$

核反应截面

反应截面的物理意义表示：一个粒子入射到单位面积内只含一个靶核的靶子上所发生反应的概率。或者说，表示一个入射粒子同单位面积靶上一个靶核发生反应的概率。

大多数情况下，反应截面通常小于或等于原子核的横截面积。其数量级约为 $10^{-24}\mathrm{cm}^{2}$ 。通常使用单位靶，记作 $\mathrm{barn}$ 或 $\mathrm{b}$ 。有：

$\begin{aligned} 1 \mathrm{b} = 10^{-24}\mathrm{cm}^2\\ 1 \mathrm{mb} = 10^{-27}\mathrm{cm}^2\\ 1 \mathrm{\mu b} = 10^{-30}\mathrm{cm}^2\\s \end{aligned}$

对于一定的入射粒子和靶核，往往有若干个反应道，对应这些散射截面的总和为核反应的 总截面。某个特定反应道的截面称为 分截面。

微分截面 用来表示反应概率的角分布，这也是一个可以直接测量的量。

我们现在来讨论 $A(a,b)B$ 的散射截面。为了方便表示，我们将入射粒子 $a$ 与靶核 $A$ 组成的状态用 $\alpha$ 表示，将出射粒子 $b$ 与剩余核 $B$ 组成的状态用 $\beta$ 表示。将核反应看作 $\alpha\rightarrow\beta$ 的跃迁。如此：根据量子力学的微扰论，得到单位时间内发生跃迁的概率为：

$W_{\alpha\beta} = \frac{2\pi}{\hbar} |H_{\alpha\beta}|^2 \frac{dn}{dE_{\beta}} \tag{6}$

其中 $H_{\alpha\beta}$ 为跃迁矩阵元， $\frac{dn}{dE_{\beta}}$ 为末态密度。

末态密度为：

$dn = \frac{4\pi p_b^2 dp_b}{(2\pi\hbar)^3} Vg_{\beta} \tag{7}$

其中 $g_{\beta}$ 为末态的统计权重。设出射粒子 $b$ 的自旋为 $I_b$ ，剩余核 $B$ 的自旋为 $I_B$ ，则得到末态的统计权重为：

$g_{\beta} = (2I_b+1)(2I_B+1) \tag{8}$

可以得到末态的态密度为：

$\begin{aligned} \frac{dn}{dE_{\beta}} &= \frac{4\pi p_b^2}{(2\pi\hbar)^3} V(2I_b+1)(2I_B+1) \frac{dp_b}{dE_{\beta}}\\ &= \frac{4\pi p_b^2}{(2\pi\hbar)^3v_b} V(2I_b+1)(2I_B+1) \frac{dp_b}{dE_{\beta}}\\ \end{aligned}$

代入 $(6)$ 得到：

$W_{\alpha\beta} = \frac{1}{\pi\hbar^4} \frac{p_b^2}{v_b}V |H_{\alpha\beta}|^2 (2I_{b}+1)(2I_{B}+1) \tag{9}$

于是 $A(a,b)B$ 的反应截面可以写为：

$\begin{aligned} W_{\alpha\beta} &= \frac{W_{\alpha\beta}}{n_av_a}\\ &= \frac{1}{\pi\hbar^4} \frac{p_b^2}{v_av_b}V^2 |H_{\alpha\beta}|^2 (2I_{b}+1)(2I_{B}+1)\\ \end{aligned} \tag{10}$

其中跃迁矩阵元将取决于原子核的内部结构。

现在我们对 $H_{\alpha\beta}$ 作一定假设，来得到有关反应截面随能量变化的一般特征。我们只考虑 $a,A$ 以及 $b,B$ 之间的库伦势垒的影响，忽略离心势垒的作用。这对于低能粒子的出射与入射的情形是适宜的。除库伦势垒外，假定跃迁矩阵元中的其余部分近似为常量。

$H_{\alpha\beta} \propto e^{-(G_a+G_b)}$

其中势垒穿透因子为：

$\begin{aligned} G_a &= \frac{2}{\hbar}\sqrt{2\mu_a} \int (\frac{Z_aZ_Ae^2}{4\pi\varepsilon_0r} - E_\alpha)^{1/2}dr\\ G_b &= \frac{2}{\hbar}\sqrt{2\mu_b} \int (\frac{Z_bZ_Be^2}{4\pi\varepsilon_0r} - E_\beta)^{1/2}dr\\ \end{aligned}\tag{11}$

现在对于几种比较典型的反应道的截面 $\sigma$ 与能量的关系进行讨论。

低能中子的弹性散射截面
$v_a = v_b$ 此时 $p_b^2/v_av_b$ 为常量。另外还有 $G_a = G_b = 0$ ，此时 $H_{\alpha\beta} \approx \mathrm{const}$ 。
得到 $\sigma(n,n)$ 为常量。（入射中子能量小于 $5\mathrm{eV}$ ）

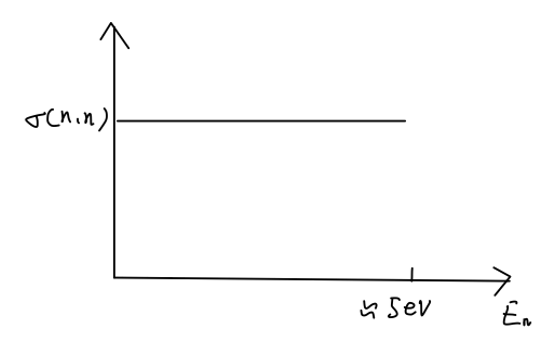
Fig：低能中子的弹性散射截面

低能中子的放能反应截面
在由低能中子引起的裂变反应中， $Q$ 值一般较大 $\sim\mathrm{MeV}$ ，出射粒子速度几乎不变。入射粒子能量 $\sim \mathrm{eV}$ 。此时 $G_b \approx \mathrm{const},G_a = 0$ 。如此 $H_{\alpha\beta} \approx \mathrm{const}$ 。
得到：

$\sigma(n,b) \propto 1/v_n$

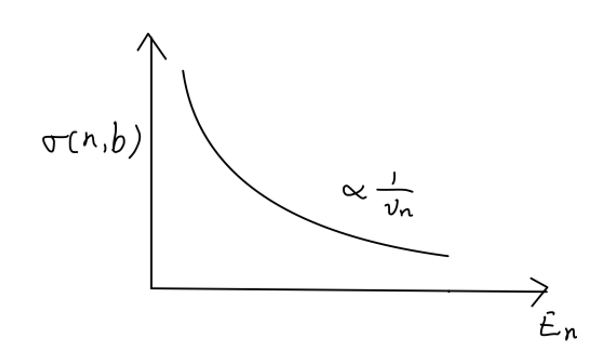
Fig：低能中子的放能反应截面

中子的非弹性散射截面
这种反应中，剩余核 $B$ 处于激发态，因而反应能 $Q$ 小于零。当入射能量 $E_{n}$ 稍大于反应阈能 $E_{th}$ 时， $E_n$ 的相对变化不大。此时 $v_n$ 约等于常量， $G_a =G_b = 0$ ， $H_{\alpha\beta} \approx \mathrm{const}$ 。
得到：

$\sigma(n,n')\propto v_{n'} \propto (E_n - E_{th})^{1/2}$

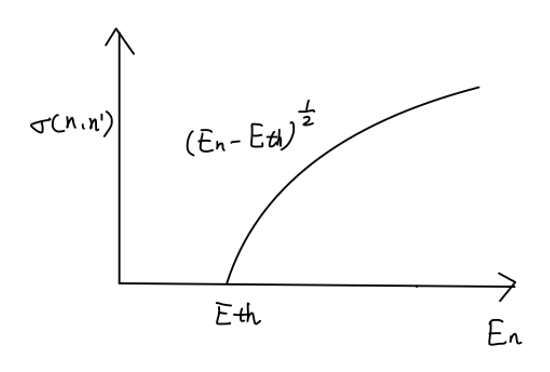
Fig：中子的非弹性散射截面

中子引起的发射带电粒子的吸能反应截面 $\sigma(n,b)$ 。类比第三类情况，此时要考虑 $G_b$ 的作用，有：

$\sigma(n,b) \propto (E_n - E_{th})^{1/2} e^{-2G_b}$

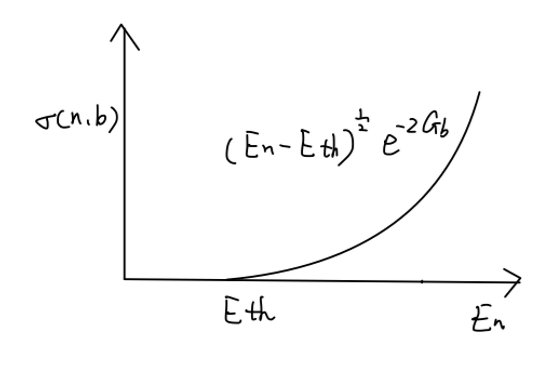
Fig：中子引起的发射带电粒子的吸能反应截面

带电离子的放能反应截面
当入射粒子能量 $E_n \ll Q$ 时， $v_b \approx \mathrm{const}$ 。此时 $G_a$ 起作用：

$\sigma(a,b) \propto \frac{1}{v_a} e^{-2G_a}$

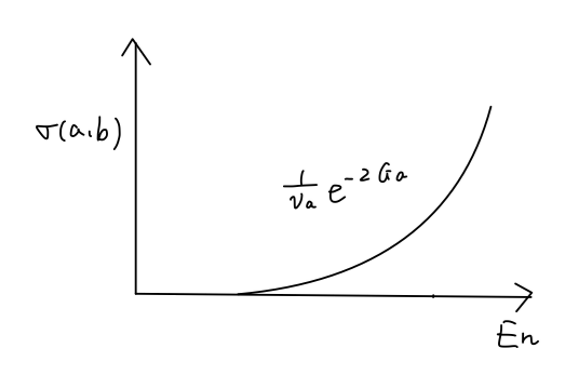
Fig：带电离子的放能反应截面

以上讨论只反映不考虑共振时的截面变化趋势。

分波分析

考虑入射粒子 $a$ 与靶核 $A$ 作用引起的反应：设 $\sigma_{sc}$ 为其 弹性散射截面， $\sigma_{\tau}$ 为 反应截面，反应截面为除弹性散射截面外的各种截面之和。总散射截面为两种截面的和：

$\sigma_t = \sigma_{sc} + \sigma_{\tau}$

我们简单考虑自旋为零的情形。我们讲截面分解为各种角动量所对应的截面之和：

$\sigma_{sc} = \sum_{l=0}^{\infty}\sigma_{sc,l} \quad \sigma_{\tau} = \sum_{l=0}^{\infty}\sigma_{\tau,l}$

其中 $\sigma_{sc,l},\sigma_{\tau,l}$ 分别代表角动量为 $l$ 的入射粒子所引起的弹性散射截面和反应截面。

考虑入射粒子为中子的情况。讲入射粒子束可以用平面波来表示。现在使用球谐函数对平面波进行展开：

$\exp(ikz) = \frac{\sqrt{\pi}}{kr}\sum_{l=0}^{\infty}\sqrt{2l+1} i^{l+1} \{ \exp(-i(kr-\frac{l\pi}{2})) - \exp(i(kr-\frac{l\pi}{2})) \} Y_{l,0}(\theta)$

其中 $\exp(-i(kr-\frac{l\pi}{2}))$ 代表入射球面波， $\exp(i(kr-\frac{l\pi}{2}))$ 代表出射球面波。考虑原子核的作用，出射球面波的振幅相位会发生变化，我们由此为出射波添加一个系数 $\eta_{l}$ 。如此波函数为：

$\psi(r)=\frac{\sqrt{\pi}}{kr}\sum_{l=0}^{\infty}\sqrt{2l+1} i^{l+1} \{ \exp(-i(kr-\frac{l\pi}{2})) - \eta_{l}\exp(i(kr-\frac{l\pi}{2})) \} Y_{l,0}(\theta)$

这里应当有 $|\eta_l| \ll 1$ ，如此可以得到远离靶核的散射波的表达式为：

$\begin{aligned} \psi_{sc} &= \psi(r) - \exp(ikz)\\ &= \frac{\sqrt{\pi}}{kr} \sum_{l=0}^{\infty}\sqrt{2l+1} i^{l+1}(1-\eta_l)\exp(i(kr-\frac{l\pi}{2}))Y_{l,0}(\theta)\\ \end{aligned}$

散射截面应当为单位时间内散射粒子数目 $N_{sc}$ 除以入射粒子通量密度 $\Phi_0$ 。 $N_{sc}$ 可以由以下式求得：

$\begin{aligned} N_{sc} &= \int j_{sc} r_0^2 \sin\theta d\theta d\phi\\ &= \frac{\hbar}{2\mu i}\int (\frac{\partial \psi_{sc}}{\partial r} \psi_{sc}^* - \frac{\partial \psi_{sc}^*}{\partial r} \psi_{sc}) r_0^2 \sin\theta d\theta d\phi\\ &= \frac{v\pi}{k^2}\sum_{l=0}^{\infty}(2l+1)|1-\eta_l|^2 \end{aligned}$

入射波为平面波，通量密度就为入射粒子的速度 $v$ 。如此，得到：

$\begin{aligned} \sigma_{sc} &= \frac{N_{sc}}{\Phi}\\ &= \sum_{l=0}^{\infty} \frac{\pi}{k^2}(2l+1)|1-\eta_l|^2\\ \sigma_{sc,l} &= \frac{\pi}{k^2}(2l+1)|1-\eta_l|^2\\ \end{aligned}$

类似的，对于反应截面，可得：

$\begin{aligned} \sigma_{\tau} &= \sum_{l=0}^{\infty} \frac{\pi}{k^2}(2l+1)(1 - |\eta_l|^2)\\ \sigma_{\tau,l} &= \frac{\pi}{k^2}(2l+1)(1 - |\eta_l|^2)\\ \end{aligned}$

总反应截面为：

$\begin{aligned} \sigma_t &= \sigma_{sc} + \sigma_{t}\\ &= \sum_{l=0}^{\infty} \frac{2\pi}{k^2}(2l+1)(1 - \mathrm{Re}\eta_l)\\ \sigma_{t,l} &= \frac{2\pi}{k^2}(2l+1)(1 - \mathrm{Re}\eta_l)\\ \end{aligned}$

有关 $\eta_l$ ，可以对不同的 $l$ 值进行具体考虑。如入射为 $l=0$ 的中子的情况，此时波函数为：

$\psi = \frac{\sqrt{\pi}}{kr}i(e^{-ikr} - \eta_0e^{ikr})Y_{0,0} = \frac{u_0}{r}Y_{0,0}$

其中径向波函数为 $u_0$ 。设 $u_i$ 为核内中子波函数的径向部分。考虑到 $u_0$ ， $u_i$ 在 $r = R = R_a + R_n$ （道半径）处连续。其对数导数应当相等：

$f \equiv (\frac{d\ln u_i}{d\ln r})_{r=R} = (\frac{d\ln u_0}{d\ln r})_{r=R}$

得到 $f$ 是相对运动动能的函数。由上式子得到：

$\eta_0 = \frac{f+ikR}{f-ikR} e^{-2ikR}$

代入弹性散射截面的表达式，得到：

$\sigma_{sc,0} = \frac{\pi}{k^2} [A_{pot} + A_{res}]^2$

其中：

$\begin{aligned} A_{pot} = 2ie^{ikR}\sin kR\\ A_{res} = -\frac{2ikR}{f_{Re} + i(f_{Im} - kR)} \end{aligned}$

其中 $A_{pot}$ 与核的内部状态无关，称为 外部散射/势散射振幅。 $A_{res}$ 与核的内部状态有关，称为 内部散射/共振散射振幅。

核反应过程与核反应机制

V. F. Weisskopf 于 1957 年对核反应过程提出了三阶段描述。它描述了核反应过程的粗糙图像。

第一阶段（独立粒子阶段）：
入射粒子接近到靶核核场作用范围内，可能发生两种情况：
- 粒子进入靶核，引起核反应
- 粒子被靶核弹出，发生弹性散射
第二阶段（复合系统阶段）：
入射粒子和靶核发生能量交换，入射粒子和靶核形成了复合体系。能量交换可能有几种方式：
- 入射粒子把能量交给靶核表面或者体内一个或几个核子，使反应直接进入第三阶段。分别称为 表面直接作用 和 体内直接作用。
- 入射粒子在核内经过多次碰撞再发射出来，称为 多次碰撞。
- 入射粒子把部分能量交给靶核后飞出，这时靶核产生集体激发，引起核的集体转动、振动等，叫做 集体激发。
以上三种方式统称为 直接作用，均保留了入射粒子的原有特性。
- 入射粒子于靶核经过多次碰撞、不断损失能量，最后停留在核内，和靶核融为一体，形成 复合核。
第三阶段（最后阶段）
复合系统分解成出射粒子和剩余核。分解出的粒子也有可能与入射粒子相同，同时剩余核处于基态，称为 弹性散射。经过复合核的弹性散射称为 复合核弹性散射，即 共振散射。独立粒子阶段所形成的散射称为 形状弹性散射，即 势散射。