线性空间

线性空间 (linear space)
线性空间（矢量空间） XX 是一个域 K\mathbb{K} 上的模。这个域 K\mathbb{K} 可以是实数域 R\mathbb{R}、复数域 C\mathbb{C} 等等。

在我们初学线性代数时，我们使用了八个公理去定义线性空间，这其实和 “域 K\mathbb{K} 上的模” 的内涵是完全一致的。我们来看：

设 u,v∈X,a,b∈Ku,v \in X,a,b\in\mathbb{K}，ee 为域 K\mathbb{K} 中的恒元。

  • 域 K\mathbb{K} 上的模 XX 是一个 阿贝尔群，存在一个群加法 “++”，XX 对于 “++” 成阿贝尔群：
    • 交换律

    u+v=v+uu + v = v + u

    • 结合律

    u+v=v+uu + v = v + u

    • 存在零元

    u+0=uu + 0 = u

    • 存在逆元

    u+(−u)=0u + (-u) = 0

  • 外部运算标量乘法 “⋅\cdot” 需要满足：
    • 分配律

    a(u+v)=au+av(a+b)u=au+bu\begin{aligned} &a (u + v) = a u + av\\ &(a + b)u = a u + b u\\ \end{aligned}

    • 标量乘法与域 K\mathbb{K} 的乘法相容

    (ab)u=a(bu)(ab)u= a(b u)

    • 域中恒元 ee 的标量乘法：

    eu=ueu = u

简而言之，线性空间是一个 K−\mathbb{K}-模。

常见的线性空间有 R3\mathbb{R}^3：三维向量空间。再比如所有系数为实数的多项式的集合 R[X]\mathbb{R}[X]，对于通常意义上的多项式加法和标量乘法，R[X]\mathbb{R}[X] 也构成一个向量空间。

我们通常将线性空间中的元素称为 矢量 (vector) 或 向量。因此线性空间也常称为 矢量空间 (vector space) 或 向量空间。

∀x∈X\forall x\in X，我们可以将其展开为：

x=xiei:=∑i=1nxiei,xi∈Kx = x^i e_i := \sum_{i=1}^{n}x^ie_i,\quad x_i\in\mathbb{K}

这里上下重复指标代表缩并，即 Einstein 求和公约。其中 {ei}\{e_i\} 为该线性空间的一组基底：

{ei,i=1,2,⋯ ,n=dim⁡(X)}\{e_i,i = 1,2,\cdots,n =\dim(X)\}

线性空间的子空间

子空间 (subspace)
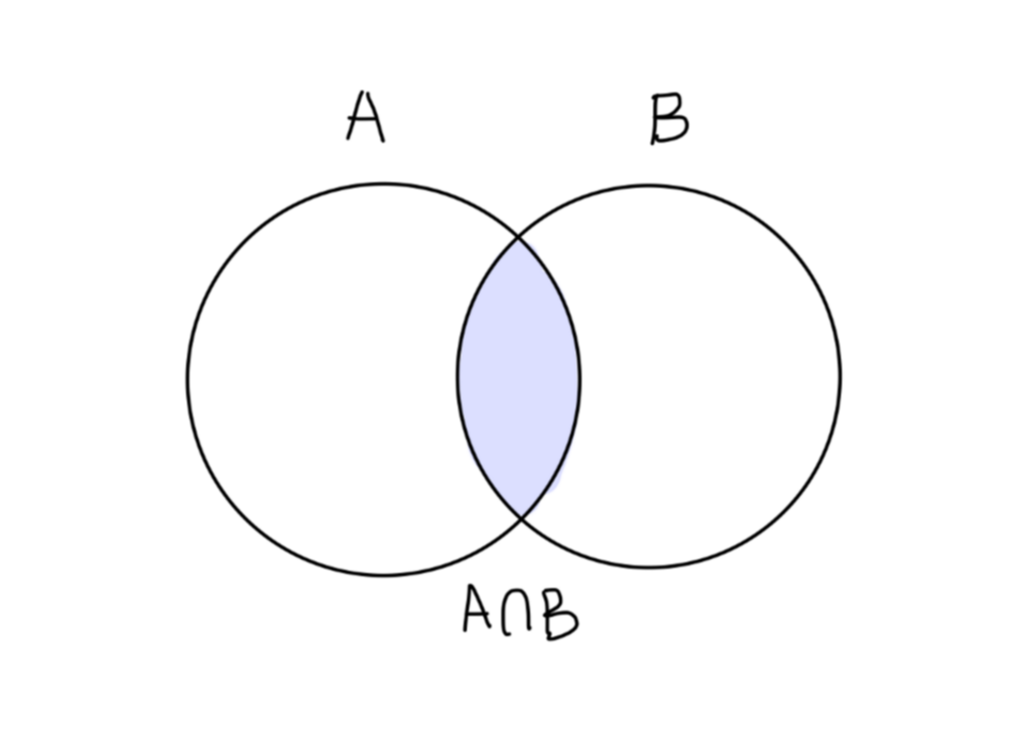
设 AA 是 XX 的一个子集，若在 XX 所有的代数操作下 AA 也是一个线性空间，则 AA 称为 XX 的一个线性子空间。

例：
设 V={v1,⋯ ,vm}V = \{v_1,\cdots,v_m\} 是 XX 中任意一组矢量，则这组向量张成的空间 Span(V)\mathrm{Span}(V) 是 XX 的一个线性子空间。
Span(V)\mathrm{Span}(V) 定义如下：

Span(V):={zivi∣zi∈K,i=1,⋯ ,m}\mathrm{Span}(V) := \{ z^iv_i| z^i \in \mathbb{K}, i =1,\cdots,m\}

线性子空间的内直和 (internal direct sum)
设 UU 和 VV 是 XX 的两个子空间，且有 U∩V={0}U\cap V = \{0\}。则 UU 和 VV 的内直和定义为：

U⊕V={u+v∣u∈U,v∈V}U \oplus V = \{u + v|u \in U,v \in V \}

注意只有当 U∩V={0}U \cap V = \{0\} 时，它们的内直和可定义。

定理
设 UU 和 VV 是 XX 的两个子空间，则 U⊕VU \oplus V 也是 XX 的子空间，且有

dim⁡(U⊕V)=dim⁡(U)+dim⁡(V)\dim(U \oplus V ) = \dim(U) + \dim(V )

不难证明，注意到 U,VU,V 可以用两组基底 {ei},{ej}\{e_i\},\{e_j\} 张成，且 U∩V={0}U \cap V = \{0\} 说明该两组基底是线性无关的。且 {ei}∪{ej}\{e_i\} \cup \{e_j\} 能张成 U⊕VU\oplus V。

线性子空间的补空间 (complementary)
设 UU 和 VV 是 XX 的两个子空间，且有

X=U⊕VX = U \oplus V

则称 VV 为 UU 的 补空间。

在上面的定义中，VV 和 UU 是相互的。即 U,VU,V 互为补空间。
但需要指出的是：给定一个 UU，它的补空间并不唯一。例如取 X=R3X = \mathbb{R}^3，U={(0,y,z)∣y,z∈R}U = \{(0,y,z)|y,z\in \mathbb{R}\}，而其补空间 VV 不唯一，可以取为：

X={(t,at,bt)∣t∈R}X = \{ (t,at,bt)| t\in \mathbb{R}\}

其中 a,ba,b 为给定实数。

线性子空间的外直和 (external direct sum)
设 XX 和 YY 是数域 K\mathbb{K} 上的两个线性空间，在卡氏积 X×YX × Y 上定义如下加法 “++” 和数乘 “⋅·”：

(x1,y1)+(x2,y2)=cλ⋅(x,y)=(λx,λy)\begin{aligned} &(x_1 ,y_1 ) + (x_2 ,y_2 ) = c\\ &\lambda \cdot (x,y) = (\lambda x,\lambda y)\\ \end{aligned}

其中 x1,x2,x∈X, y1,y2,y∈Y, λ∈Kx_1,x_2 ,x \in X,\ y_1 ,y_2 ,y \in Y,\ \lambda \in \mathbb{K}，则 X×YX \times Y 配以 “++” 和 “⋅\cdot” 成为一个线性空间，称为 XX 和 YY 的 (外)直和，并记为 X⊕YX \oplus Y，即我们有：

X⊕Y=(X×Y,+,⋅)X\oplus Y = (X \times Y,+,\cdot)

有时候也将 X⊕Y=(X×Y,+,⋅)X\oplus Y = (X \times Y,+,\cdot) 中矢量的加法 “+”“+” 也记为 “⊕\oplus”，即有：

(x1,y1)⊕(x2,y2)=(x1+x2,y1+y2)(x_1,y_1)\oplus(x_2,y_2) = (x_1 + x_2 ,y_1 + y_2 )

定理
设 UU 和 VV 是 XX 的两个线性子空间，且 XX 等于 UU 和 VV 的内直和。现将 UU 和 VV 看作两个独立的线性空间，则它们的外直和与 XX 同构。

其中：数域 K\mathbb{K} 上的两个线性空间 V,V′V,V' 同构是指：存在一个双射 σ:V→V′\sigma: V\rightarrow V' 保持加法与数乘的结构：
即 ∀k∈K, u,v∈V\forall k\in \mathbb{K},\ u,v \in V 有：

σ(u+v)=σ(u)+σ(v)σ(ku)=kσ(u)\begin{aligned} \sigma(u+v) &= \sigma(u)+\sigma(v)\\ \sigma(ku) &= k\sigma(u)\\ \end{aligned}

线性映射

线性映射 (linear mappings)
设 XX 和 YY 是某个域 K\mathbb{K} 上的两个线性空间。映射 f:X→Yf : X \rightarrow Y 称为线性映射，若：

∀α,β∈K, ∀x,y∈X,f(αx+βy)=αf(x)+βf(y)\forall \alpha,\beta \in \mathbb{K},\ \forall x,y \in X,\quad f(\alpha x + \beta y) = \alpha f(x) + \beta f(y)

线性映射的核 (kernal)
设 f:X→Yf : X \rightarrow Y 为线性映射，XX 中的子集 {x∣f(x)=0}\{x|f(x) = 0\} 称为 ff 的核。记为 ker⁡f\ker f。

定理
设 f:X→Yf : X \rightarrow Y 为线性映射，则 ker⁡f\ker f 是 XX 的线性子空间。若 ker⁡f={0}\ker f = \{0\}，则 ff 是单射。

容易证明 ker⁡f\ker f 为 XX 的线性子空间：
∀ x1,x2∈ker⁡f, ∀ α,β∈K\forall\ x_1,x_2\in \ker f,\ \forall\ \alpha,\beta \in \mathbb{K}。由线性映射的性质可得：

f(αx1+βx2)=αf(x1)+βf(x2)=0⇒αx1+βx2∈ker⁡ff(\alpha x_1 + \beta x_2) = \alpha f(x_1) + \beta f(x_2) = 0 \Rightarrow \alpha x_1 + \beta x_2\in \ker f

不难证明也将满足线性空间的其他公理。且显然有 ker⁡f⊂X\ker f \subset X。

另外：利用反证法，若 ff 不是单射，容易得到存在非零元素属于 ker⁡f\ker f。

线性映射的像 (image)
设 f:X→Yf : X \rightarrow Y 为线性映射，则可将其像记为 imf\mathrm{im} f。

定理
设 f:X→Yf : X \rightarrow Y 为线性映射，则 imf\mathrm{im}f 是 YY 的子空间。

定理
设 f:X→Yf : X \rightarrow Y 为线性映射，则：

dim⁡(X)=dim⁡(ker⁡f)+dim⁡(imf)\dim(X) = \dim(\ker f) +\dim(\mathrm{im}f)

证明：
设 XX 的维度为 nn，ker⁡f\ker f 的维度为 mm，我们只需要证明 imf\mathrm{im}f 的维度为 n−mn-m 即可。由于 dim⁡X=n\dim X = n，我们可以找到一个极大线性无关基底组：

{ei,i=1,⋯ ,n}\{e_{i},i = 1,\cdots,n\}

由于 Imf\mathrm{Im} f 为线性空间，可以取以下基底组：

{f(ei),i=1,⋯ ,n}\{f(e_{i}),i = 1,\cdots,n\}

该基底是完备的，但并不一定是线性独立的。考虑到 ker⁡f\ker f 的维度为 mm，因此将存在 mm 个线性独立的方程：

f(amiei)=0=amif(ei)f(a^{i}_{m}e_{i}) = 0 = a^i_m f(e_i)

因此可以得到 {f(ei)}\{f(e_i)\} 的维度为 m−nm-n。即有：

dim⁡(X)=dim⁡(ker⁡f)+dim⁡(imf)\dim(X) = \dim(\ker f) +\dim(\mathrm{im}f)

对偶空间

线性映射的空间
由 XX 到 YY 的所有线性映射形成一个集合。我们将其记为 L(1)(X;Y)\mathscr{L}^{(1)} (X;Y)，在这个集合上我们可以引入一个内部加法：

(f+g)(x)=f(x)+g(x)(f + g)(x) = f(x) + g(x)

和一个外部标量乘积：

(λf)(x)=λf(x),λ∈K(\lambda f)(x) = \lambda f(x),\quad \lambda \in \mathbb{K}

这样由 XX 到 YY 的所有线性映射形成一个集合: L(1)(X;Y)\mathscr{L}^{(1)} (X;Y)，也形成域 K\mathbb{K} 上的线性空间。

（代数）对偶空间 (Algerbraic dual space)
取 YY 为域 K\mathbb{K}，则 L(1)(X;K)\mathscr{L}^{(1)} (X;\mathbb{K}) 是 XX 上 K\mathbb{K} 值线性函数形成的空间，称为 XX 的代数对偶空间。记为 X∗X^*，其中的元素可以记为：x∗,y∗,⋯x^*,y^*,\cdots。

定理
设 XX 是有限维空间，则 X∗X^* 和 XX 的维数相同。

证明：
设 x∈X,f∈X∗x\in X,f\in X^*，xx 可展开为 x=xieix = x^ie_i，则有：

f(x)=xif(ei)f(x) = x^i f(e_i)

因此，一个线性函数在矢量上的作用可完全由其在基底 {ei}\{e_i\} 上的作用决定。考虑 X∗X^* 内的基底为 {e∗i}\{e^{*i}\}，我们完全可以选取一组特殊的基 {e∗i}\{e^{*i}\} 使得：

e∗i(ej)=δji,j=1,⋯ ,ne^{*i}(e_j) = \delta^{i}_{j},\quad j = 1,\cdots,n

那么就有：

f(x)=f(ei)xi=f(ei)e∗i(x)f(x) = f(e_i)x^i =f(e_i)e^{*i}(x)

其中：

fi=f(ei)∈Kf_i = f(e_i) \in \mathbb{K}

因为 xx 任意，可以得到：

f=fie∗if = f_i e^{*i}

因此可以发现：任意一个给定的线性函数，都可以由 {e∗i,i=1,⋯ ,n}\{e^{*i},i=1,\cdots,n\} 展开。可以证明这个展开是唯一的。

XX 与 X∗X^* 的对偶是相互的。有：

(X∗)∗=X(X^{*})^* = X