广义相对论的数学基础（九）：拓扑空间连续映射

拓扑空间连续映射

连续映射

一点处连续
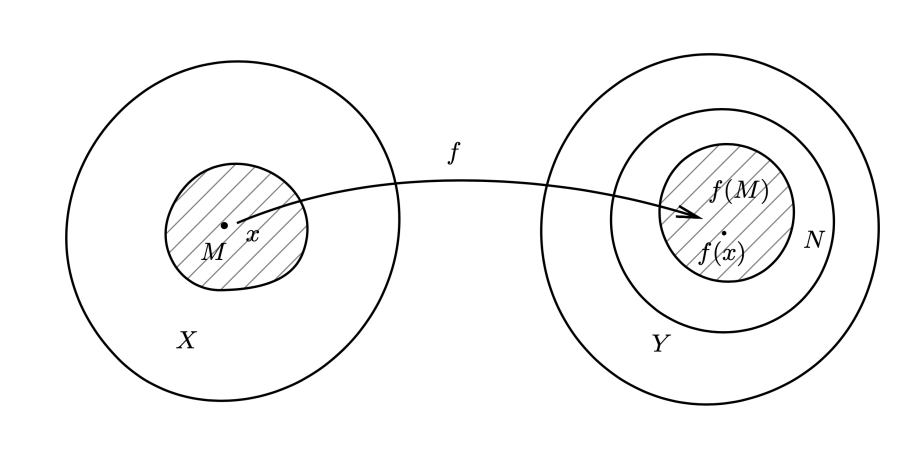
设 $f$ 是由拓扑空间 $X$ 到另一个拓扑空间 $Y$ 的映射。 $f$ 称为在点 $x \in X$ 是连续的，如果对于 $f(x)$ 的任意一个邻域 $N \subset Y$ ，都存在一个 $x$ 的一个邻域 $M \subset X$ 使得 $f(M) \subset N$ 。

连续映射

以下两种定义是等价的：

$f$ 称为在 $X$ 上连续，若其在 $X$ 的每一点都连续。
映射 $f : X \rightarrow Y$ 称为是连续的，若对于 $Y$ 中的每一个开集 $U$ ，集合 $f^{-1} (U)$ 在 $X$ 中是开集。

若 $X$ 的拓扑是离散拓扑，则所有映射 $f:X\rightarrow Y$ 都是连续的。
若 $Y$ 的拓扑是平凡拓扑，则所以的 $f$ 也是连续的。

同胚

同胚 (homeomorphism)
设 $f : X \rightarrow Y$ 是一个双射（ $f^{-1}$ 存在），若 $f$ 和 $f^{-1}$ 都连续，则称 $f$ 为同胚。

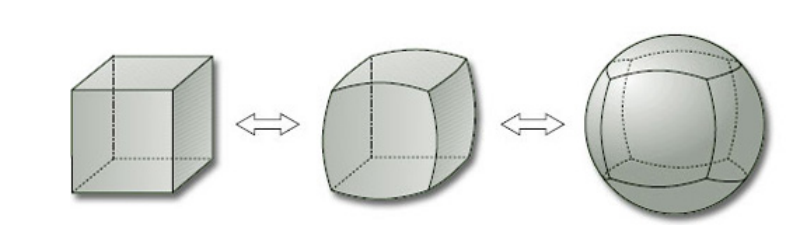
如上图所示。直观上来说：同胚可以理解为一种对点不撕裂，不粘合，连续的变换。

不撕裂：这种操作可以当作映射
不粘合：所成的映射是单射
连续的：邻近的点变换后仍保持邻近（连续映射）

所谓的 拓扑不变量 是指拓扑空间的在同胚下被保持的某些性质。例如：连通性，紧致性等等。拓扑不变量在数学和物理上是非常重要的。

反过来，拓扑不变量是否一定要求在同胚变换下不变？答案是否定的。一些拓扑不变量只要求映射为同伦，并不一定要求同胚。

相对拓扑和乘积拓扑

对于拓扑空间 $X$ 的子集，以及拓扑空间的直积，它们可以拥有由 $X$ 的拓扑诱导的拓扑。

相对拓扑 (relative topology)
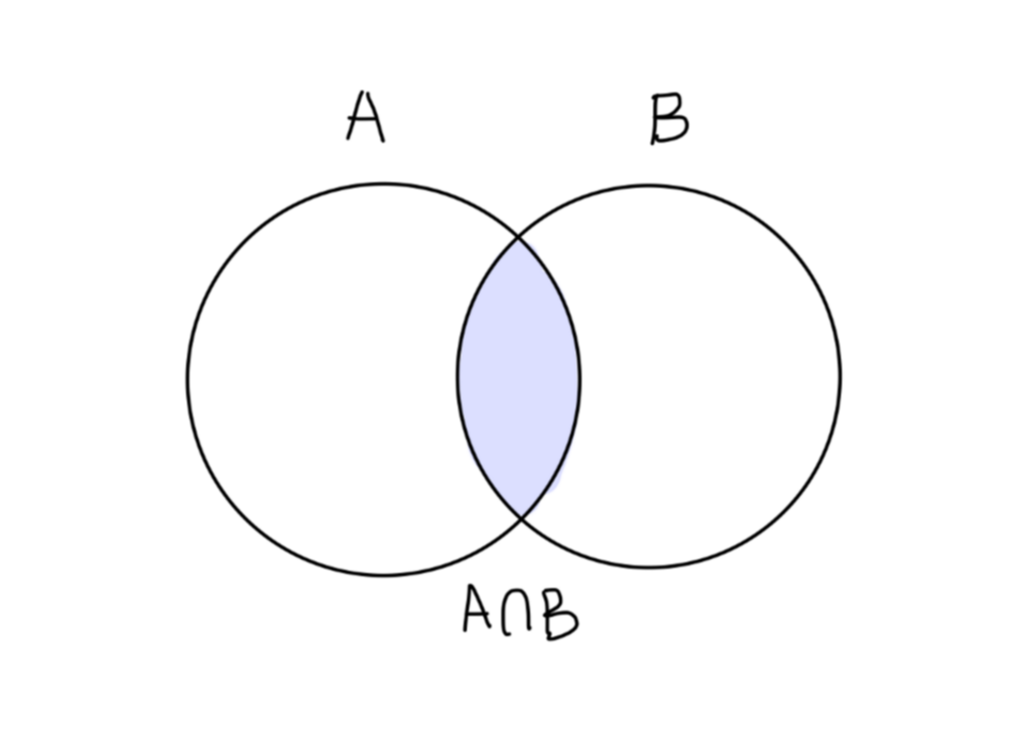
设 $A \subset X$ ， $X$ 的拓扑为 $\mathscr{U}$ 。子集 $A$ 的相对拓扑定义为：

$\mathscr{U}_A = \{A \cap U|U \in \mathscr{U} \}$

欧氏空间
$S^{n-1}$ 是 $\mathbb{R}^n$ 的子集， $\mathbb{R}^n$ 的通常拓扑诱导出 $S^{n-1}$ 上的相对拓扑使其成为拓扑空间。

乘积拓扑 (product topology)
设 $(X,\mathscr{U} )$ 和 $(Y,\mathscr{V} )$ 是两个拓扑空间。直积 $X \times Y$ 上可以赋予拓扑 $\{(U,V )|U \in \mathscr{U} ,\mathscr{V} \in V \}$ 这个拓扑称为 $X \times Y$ 上的乘积拓扑。

欧氏空间
在 $\mathbb{R}^n = \mathbb{R}\times \cdots \times \mathbb{R}$ 中可以认定“开球”：

$\sum_{i=1}^{n}(x^i-a^i)^2 < b^2$

为开集，这是欧氏空间的通常拓扑。 $\mathbb{R}$ 上可以赋予通常拓扑，也可以赋予 $\mathbb{R}^n$ 以乘积拓扑，这个拓扑与 $\mathbb{R}^n$ 中的通常拓扑是等价的。

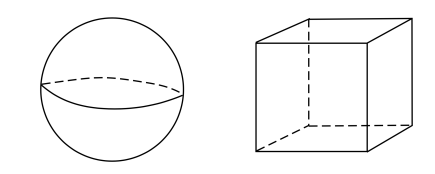
左边为开球拓扑，右边为乘积拓扑。

拓扑的等价
集合 $X$ 上的两个拓扑 $U = \{U _ i \}$ 和 $V = \{V _ j \}$ 称为是等价的，若任意一个非空的 $U_ i$ 包含某个非空的 $V_ j$ 。反过来，每个非空的 $V_ j$ 也包含了某个非空的 $U_ i$ 。

拓扑结构和代数结构

如果集合 $X$ 上还有其他一些数学结构，在 $X$ 上引入拓扑结构时，还应使得拓扑结构和其他的数学结构相容。

拓扑群

拓扑群 (Topological groups)
设 $(X,\cdot)$ 是一个群。若 $X$ 上存在一个拓扑使得所有的乘法和求逆是连续的，即如下两个映射：

$\begin{aligned} &X \times X \rightarrow X, (x,y) \mapsto x \cdot y = xy ,\\ &X \rightarrow X, x \mapsto x ^{-1}\\ \end{aligned}$

是连续的。拓扑群也称为连续群。

有很平庸的例子，例如 $Z_2$ 群赋以平庸拓扑后成为拓扑群。但这种意义的连续性是平庸的。物理上我们关心的是局部上和欧氏空间同胚的连续群。

矩阵群
一般线性变换群定义为：

$\mathrm{GL}(n,\mathbb{R}) := \{A \in M(n,\mathbb{R})|\det A\neq 0 \}$

其中 $M(n,\mathbb{R}) = \mathbb{R}^{n^2}$ 是所有 $n \times n$ 矩阵形成的集合。我们可以在 $GL(n,\mathbb{R})$ 赋以 $\mathbb{R} ^{n^2}$ 的通常拓扑诱导的相对拓扑使其形成一个连续群。

在 Hilbert’s problems 中，第五个问题大意为：连续群是否具备李群结构。这个问题在 1953 年，由三个美国数学家解决：对局部上和欧氏空间同胚的连续群，群结构使得其具备可微结构，使之成为李群，甚至是一个实解析群。

拓扑矢量空间

拓扑矢量空间
域 $\mathbb{K}$ 上的线性空间称为是拓扑线性空间，若它可以赋予一个拓扑使得矢量加法，标量积运算都是连续的，即映射：

$\begin{aligned} &X \times X \rightarrow X , (x,y) \mapsto x + y\\ &\mathbb{K} \times X \rightarrow X , (\lambda,x) \mapsto \lambda x\\ \end{aligned}$